双渠道模式下的品牌方与带货主播的博弈模型

朱燕杰，陆媛媛

（吉林师范大学数学与计算机学院，吉林 四平 136000）

0 引言

互联网经济的快速崛起和发展，促使越来越多的消费者选择线上购物，品牌方也顺应消费者在线上开辟了销售渠道，纷纷在电商平台运营自己的官方旗舰店.近几年，直播带货日渐火爆，品牌方也把目光汇聚于此，开启主播带货模式.品牌方同时拥有线上旗舰店直销和主播直播带货两种销售渠道.由两种渠道构成的供应链称为双渠道供应链.同单渠道销售相比，品牌方选择双渠道运营，商品的曝光量会增加，并且品牌方收到的商品反馈会更多，以便品牌方及时实现产品的升级，更好地拓宽市场.

电商平台、品牌方和带货主播三方通过消费者联系起来，且利益冲突也逐渐加剧.因此，研究双渠道模式下三方的博弈模型，分析最优决策和最大利润，可以为电商平台、品牌方和带货主播三方的运营提供理论指导，并且为互联网经济的研究提供一定的补充.

许多专家和学者都对直播带货有自己的独到见解.柴建华等［1］对直播带货模式进行探究，从直播团队分工到直播带货流程都进行了详细的探析；郑棋中［2］从电商直播入手，分析了电商直播的发展现状，指出了电商直播面临的挑战，最后为电商直播发展提出相应的建议；黄荣晟［3］首先分析了电商直播带货的营销模式，其次点出数字化背景下电商直播模式还需改进的地方，最后阐述从电商营销模式得到的创新启示；刘平胜等［4］通过对问卷调查得到的数据进行分析，发现了影响直播带货中粉丝购买行为的几个因素.也有许多学者对电商平台和品牌方进行研究，李晓静等［5］分析交叉竞争环境下，平台直销与平台分销渠道对供应链各成员决策行为的影响；罗列英等［6］发现在平台佣金模式下，敏感强度是制造商渠道选择的决定性因素；陆媛媛等［7］研究了政府补贴下的绿色供应链模型；陆媛媛等［8］建立了在直播平台推广支持下的PEA 三方Stackelberg 博弈模型；梁喜等［9］分析在制造商主导的双渠道供应链中，三种不同双渠道结构下重要参数对其他经济变量的影响；王磊等［10］将公平关切概念引入双渠道供应链，研究公平观念如何影响渠道定价策略；王文宾等［11］考虑到电商平台对消费者强大的吸引力，建立了由供应商和平台商构成的基于电商平台混合销售的供应链模型.但很少有研究双渠道模式下品牌方与带货主播的博弈模型.

本文在双渠道模式下，建立电商平台、品牌方与带货主播三方之间的Stackelberg 博弈模型，以利润最大化为目标，研究电商平台向品牌方抽取的最优佣金率、品牌方给带货主播的最优抽成、品牌方旗舰店推广的最优努力水平和带货主播的最优努力水平与三方的最大利润问题，并分析直播消费偏好等重要参数对最优决策的影响.

1 问题描述

本文研究的是双渠道模式下品牌方与带货主播的博弈模型.选取电商平台、品牌方和带货主播为博弈方，电商平台确定向品牌方抽取的佣金率，品牌方确定给带货主播的抽成以及自己旗舰店推广的努力水平，带货主播确定自己的努力水平.电商平台的主要收益是从品牌方抽取的佣金，品牌方的主要收益是官方旗舰店和带货主播直播带货的商品销售利润，还要扣除给电商平台的佣金和给带货主播的抽成，带货主播的主要收益是品牌方给的抽成.

2 模型假设与符号说明

本文暂不考虑价格对销量的影响，因此，假设官方旗舰店和主播直播带货时的销售价格相同，由品牌方统一定价为p.

商品的总需求为a，消费者的直播消费偏好为λ，且0 ＜λ＜1.假设消费者在线上不同渠道的购买需求对努力程度的敏感系数相同.α为消费者需求对努力水平的敏感系数，β为线上不同渠道之间努力水平的交叉影响系数，且0 ＜β＜α.品牌方线上双渠道的需求表达式：消费者通过官方旗舰店购买的商品销售量为D1=(1 -λ)a+αx-βy，消费者通过带货主播直播带货时购买的商品销售量为D2=λa+αy-βx.

品牌方在运营旗舰店时，会将官网首页设计得简洁生动，以突出自己产品的特色；带货主播往往通过制作精美小视频等方式提前为消费者种草，在直播间也会花费较多的时间努力地推销商品，可以说品牌方和带货主播为了得到更多的商品销售量，都会付出较多努力，体现为一定的时间、金钱和精力，因此，会产生一定的努力成本.本文假设品牌方旗舰店和带货主播的努力程度互不影响，为了方便计算，假设努力成本系数相同均为k且k＞0.品牌方旗舰店推广的努力成本为，且；带货主播的努力成本为，且，具体文中所用到的符号说明如表1所示.

表1 符号说明

3 模型建立及求解

3.1 模型建立

根据假设得到三方的利润函数如下：

（1）电商平台的利润函数为

（2）品牌方的利润函数为

（3）带货主播的利润函数为

3.2 模型求解

定理1 当品牌方决定给带货主播的抽成为s和旗舰店推广的努力水平为x时，带货主播以自身利润最大为目标，确定自身的最优努力水平为

证明将带货主播直播的销售量D2=λa+αy-βx带入式（3）中，得到带货主播的利润函数为

此时

解得

证毕.

定理2 当电商平台向品牌方抽取的佣金率为t，且0 ＜t＜1 -时，品牌方以自身利润最大为目标，确定给带货主播的最优抽成s和旗舰店推广的最优努力水平x分别为

证明将带货主播的努力水平y=品牌方旗舰店的销售量D1和带货主播直播的销售量D2代入式（2）中，得到品牌方的利润函数

分别对s和x求偏导，有

解得驻点为

因为Hessian矩阵为

（1）一阶顺序主子式

（2）二阶顺序主子式

由于 |H|=p2(2α2-β2)＞0恒成立，因此，品牌方的利润函数π2(s,x)是关于品牌方给带货主播的抽成s和品牌方旗舰店推广的努力水平x的凹函数，即品牌方的利润函数π2(s,x)在驻点处取得极大值.

其中，f （α）为反应动力学方程，k （ T）是与温度相关的反应速率；常采用的是阿尼乌斯公式（3），E为活化能，A为指前因子，R为通用气体常数[25]。在非等温动力学反应研究中，将温度T随时间t变化的升温速率β= T t代入式（1）即可得到非等温动力学方程：

当参数条件满足0 ＜t＜1 -时，即

易于验证品牌方给带货主播的抽成s和品牌方旗舰店推广的努力水平x均为正数，即有最优解为

证毕.

因此，当电商平台抽取较低的佣金时，品牌方会增大给带货主播的抽成促使带货主播努力工作和增加旗舰店推广的努力水平，从而增加商品的销售量，实现自身利润的最大化.

将带货主播的努力水平y和品牌方旗舰店推广的努力水平x带入D1+D2中，得到

此时

解得

证毕.

3.3 系统最优决策和最大利润

将式（6）代入式（5）得

因此，当消费者偏向于通过直播购买商品时，电商平台会降低向品牌方抽取的佣金率，品牌方会降低给带货主播的抽成，带货主播也会降低自己的努力水平，以增大各自的利润.

将x*和y*代入D1+D2和D2中，得到品牌方的总销售量D1+D2和带货主播直播的销售量D2为

将式（6）—（8）、D1+D2和D2，分别带入π1(t*)，π2(s*,x*)和π3(y*)，得到电商平台、品牌方和带货主播的最大利润：

其中：C=α2-β2；E=p-kaA.

4 算例分析

4.1 算例分析

目前，线上购物是非常流行的购物方式，淘宝作为最大的线上购物平台，是大多数品牌方和消费者的首选.假设系统参数为a=1 000，p=100，k=0.01，α=0.4，β=0.1，λ=0.1，分析电商平台、品牌方和带货主播的最优决策和最大利润，结果如表2所示.

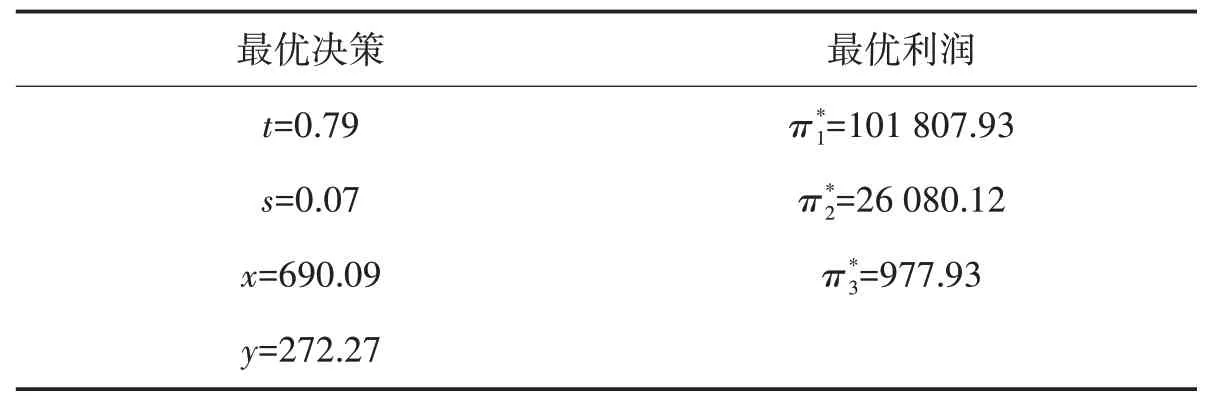
表2 算例最优结果

由表2 可知，当消费者偏向于在品牌方旗舰店购买商品时，电商平台会向品牌方抽取较多的佣金，品牌方给带货主播的抽成较低，品牌方旗舰店推广的努力水平会大于带货主播的努力水平.此外电商平台和品牌方的最终利润会较高，带货主播由于品牌方给的抽成较小和直播时商品的销售量较低，所以最后的利润较低.

4.2 努力成本系数分析

当参数条件满足所设范围时，有如下结论：

（1）电商平台向品牌方抽取的最优佣金率t*与努力成本系数k成正相关，即努力成本系数逐渐增大，电商平台抽取的最优佣金率也随之增加，如图1所示；

图1 努力成本系数对电商平台向品牌方抽取的最优佣金率的影响

（2）品牌方给带货主播的最优抽成s*与努力成本系数k成负相关，即努力成本系数逐渐增大，品牌方给的最优抽成随之减小，如图2所示；

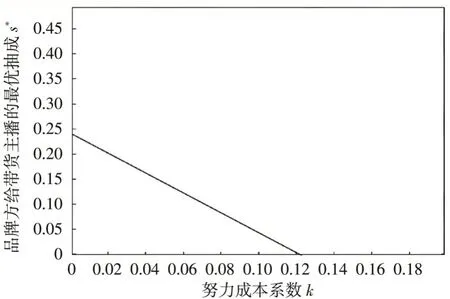
图2 努力成本系数对品牌方给带货主播的最优抽成的影响

（3）品牌方旗舰店推广的最优努力水平x*与努力成本系数k成负相关，即努力成本系数逐渐增大，品牌方的最优努力水平随之降低，如图3所示；

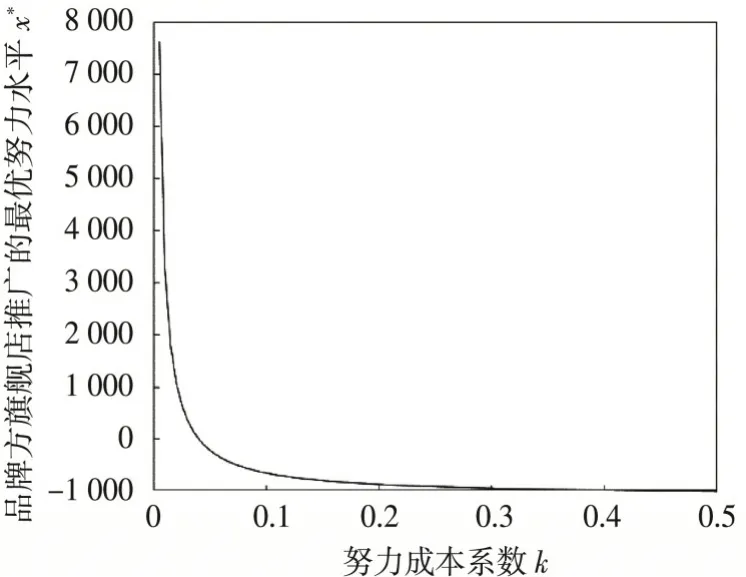
图3 努力成本系数对品牌方旗舰店推广的最优努力水平的影响

（4）带货主播的最优努力水平y*与努力成本系数k成负相关，即努力成本系数逐渐增大，带货主播的最优努力水平随之降低，如图4所示.

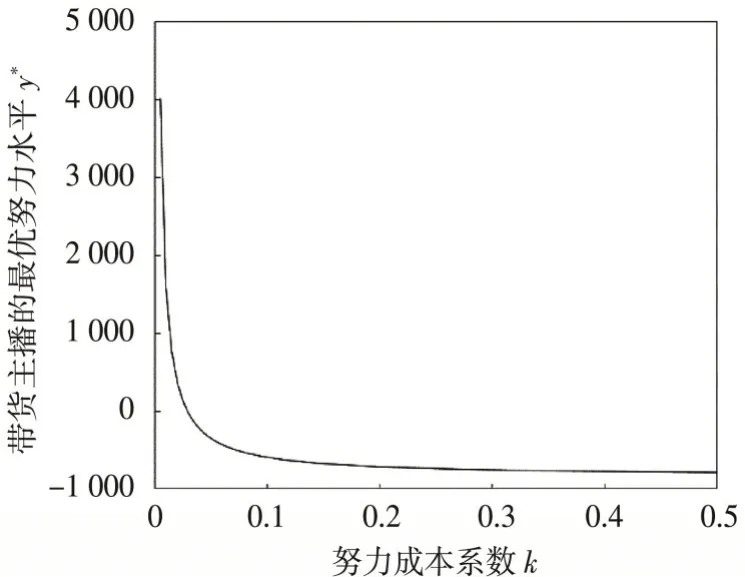
图4 努力成本系数对带货主播的最优努力水平的影响

5 结语

本文在双渠道模式下，建立电商平台、品牌方与带货主播之间的三方博弈模型，以三方利润最大化为目标，求出三方的最优决策和最大利润函数.通过博弈模型的研究不难发现，相较于传统的单渠道线下销售，线上双渠道销售好处颇多，在某些程度上可以实现各博弈方的共赢，因此，研究双渠道销售模式为供应链的决策提供参考依据.