求解旅行商问题的改进k-opt遗传算法

赵 涛,叶志伟, 宗欣露, 潘 虎

(湖北工业大学计算机学院, 湖北 武汉 430068)

旅行商问题(travelling salesman problem,TSP)是组合优化领域的经典问题。其可描述为一个商人从任意城市出发,不重复不遗漏地访问每一个城市,最后返回出发地,其目标是找出一条包含所有城市的最短路径。TSP问题是一个NP问题,对车辆路径、网络路由和车间调度等领域有重要参考价值。许多学者深入研究并提出了线性规划、动态规划、分支定界和k-opt等传统方法,这些方法在小规模TSP问题中能获得较优的求解方案。随着数据规模逐渐增大,上述方法在中大规模TSP问题求解时容易陷入局部最优解,且时间复杂度也随之增加。针对中大规模TSP问题,群智能算法如蚁群优化算法(ACO)[1-2]、粒子群优化算法(PSO)[3]、模拟退火算法(SA)[4]和遗传算法(GA)[5]等能在可期待的时间范围内获得可接受的解决方案,因此被更多的学者关注。

最近,谢聪[6]提出一种改进离散蝴蝶优化算法,利用贪婪策略初始化种群,结合2-opt方法、4-opt方法(双桥实验)和模拟退火提升算法寻优能力,但引入双桥实验使得算法时间复杂度很高。Karuna和Kusum[7]在灰狼优化算法(grey wolf optimizer,GWO)中引入汉明距离使其适用于组合优化问题,利用2-opt方法增强局部寻优能力。Zhang[8]在离散布谷鸟搜索算法中利用k-means算法将中大规模TSP问题划分为多个小规模TSP问题,以此来加速中大规模TSP问题的运行效率。但由于不同规模城市之间缺乏交互能力,使得最终的求解效果较差。Zhang和Yang[9]提出一种基于麻雀搜索算法(sparrow search algorithm, SSA)的离散麻雀搜索算法(discrete sparrow search algorithm, DSSA),利用麻雀的分工作业机制和全局扰动策略平衡算法的探索和开发能力,提高了算法跳出局部最优解的能力,同时利用2-opt方法增强局部搜索能力,取得了比离散灰狼算法更好的效果。k-opt方法或其变形方法在上述算法均得到有效利用。

与此同时,许多处理连续型优化问题的新型算法在探索方面获得极大优势,而处理连续性问题的算法难以完全适用于离散优化问题。因此,针对离散问题的局部优化算子被越来越多的学者关注,针对TSP问题的k-opt方法成为该问题在局部优化的首先方案。Osaba等人[10]动态化调整离散蝙蝠算法,其中2-opt和3-opt方法分别用于短距离和长距离优化,该操作能够有效地缓解算法陷入局部最优,从而根据种群个体潜力挖掘更优方案;Huang等人[11]同样在离散青蛙跳跃算法引入2-opt方法优化精英个体,在扰动因子的基础上强化算法搜索能力;Ahmet等人[12]在树种算法中加入大量交换、逆转和插入等扰动因子扩大全局探索能力,最终仍然通过2-opt方法局部搜索;Zhong等人[13]在离散鸽群优化算法中定义逆运算符、块插入运算符和交换运算符等扰动因子加强全局探索,采用模拟退火算法、2-opt方法和3-opt方法作为局部搜索因子,既能保证种群多样性,又能确保每个个体方案的优质性。

上述引入k-opt方法的算法,其算法时间复杂度较高。针对k-opt方法的高时间复杂度问题,本文优化原始k-opt方法提出一种求解TSP问题的改进遗传算法。一方面,利用改进遗传算法的交叉变异机制(交换、逆转、插入)进行全局搜索,融合深度搜索、分层结构和禁忌表等策略强化全局搜索能力;另一方面,引入改进的k-opt方法增强局部搜索能力。算法的探索和开发能力在该机制下均得到增强。最后通过实验证明该算法能够高效地求解TSP问题,同时获得解的质量较佳。

1 旅行商问题

旅行商问题可表示为一个无向图G=(S,E)。其中,S={1,2,…,N}表示顶点集,E为边集,边eij∈E,(i,j∈S,i≠j)。设cij为eij的距离,决策变量

该问题的优化目标如下:

s.t.∑j≠ixij=∑i≠jxji=1,i∈S

∑i≠jxij≤|V|-1,V⊂Sxij∈{0,1},i,j∈S

其中,|V|表示集合S中的顶点个数。第一个约束条件表示每个顶点仅和两条边连接,第二个约束条件表示不会产生任何一条子回路。式(2)即本文需要优化的目标,该问题是一个典型的组合优化问题,当前没有确定的算法能在多项式时间范围内找到全局最优解。

2 k-opt方法及其改进

针对TSP问题,Lin[14]在1973年提出k-opt方法优化当前路径。该方法简单有效,能在局部范围内根据当前解寻找更优解,但求解效率受数据规模影响较大。本文改进原始k-opt方法提高局部搜索运行效率。

2.1 原始2-opt和3-opt方法

图1为2-opt优化过程,该方法选择两个不相邻的点i、j,根据下式寻找更短路径。

D(i,i+1)+D(j,j+1)>D(i,j)+D(i+1,j+1)

其中D(i,j)表示i、j两点之间的距离。若条件成立,则逆转序列L(i+1,j)。其中L(i,j)表示现有路径中起点为i终点为j的路径序列。通过对现有序列不断优化,最终构建一个更短序列。同理,图2为3-opt优化过程,该方法选择三个不相邻的点i、j、k,根据下式优化当前路径。若条件成立,则逆转序列L(j+1,k)。

D(i,i+1)+D(j,j+1)+D(k,k+1)>D(i,k)+D(i+1,j+1)+D(j,k+1)

Helsgaun[15]系统地讨论了k-opt方法中不同k取值的优缺点。2-opt和3-opt方法是基于贪心搜索的优化过程(图1、2),因此以上方法也会继承贪心搜索的缺点,即最终导致陷入局部最优解。同时,2-opt和3-opt方法的时间复杂度和数据规模息息相关。理论上,2-opt方法逆转序列次数最多为O(n2),3-opt方法逆转序列次数最多为O(n3)。

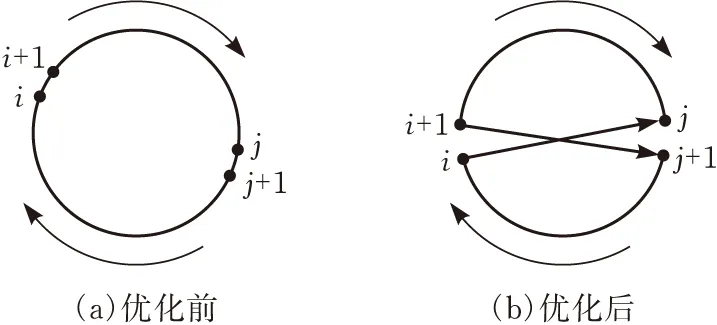
图1 2-opt方法优化过程

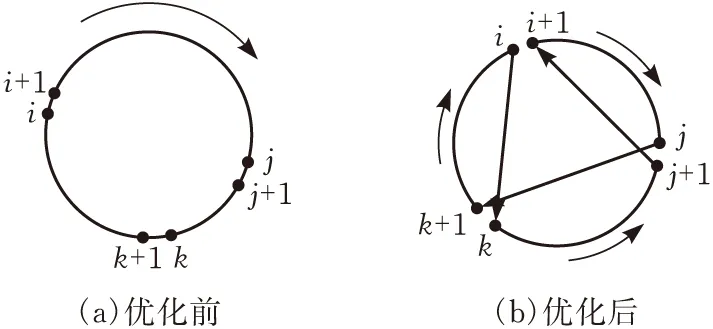
图2 3-opt方法优化过程

2.2 改进的2-opt和3-opt方法

为缓解2-opt和3-opt方法过早地陷入局部最优解,提出改进的2-opt和3-opt方法。在改进的2-opt方法中,根据当前节点i找出与自身不相邻的所有后续节点的集合J,构造集合如下:

Diff2=D(i,i+1)+

D(J,J+1)-D(i,J)-D(i+1,J+1)

其中,集合Diff2表示所有后续节点与当前节点i发生序列交换后的差异。在集合Diff2中找出最大值max_S2,若条件max_S2>0成立,则逆转max_S2对应的节点j和节点i之间的序列,即逆转当前序列L(i+1,j)。在改进的3-opt方法中,根据当前节点i,j找出与自身不相邻的所有节点的集合K,构造集合Diff3

式中：g(α),h(1-α)为分配函数，满足以下条件：① g(0)=0,g(1)=1,h(0)=0,h(1)=0；② 0≤g(α)≤1,0≤h(1-α)≤1,α∈[0,1]；③ g(α),h(1-α)随α的增大，严格递增。

Diff3=D(i,i+1)+D(j,j+1)+D(K,K+1)-

D(i,K)-D(i+1,j+1)-D(j,K+1)

与原始2-opt方法相比,改进后的2-opt算法逆转序列次数不超过O(n);改进后的3-opt方法逆转序列次数不超过O(n/2)。其次,对于任意节点,改进后的2-opt方法最多逆转序列1次,而原始的2-opt算法最多逆转序列n-2次。

3 改进的k-opt遗传算法

本文提出一种改进的k-opt遗传算法求解TSP问题。首先,在原始遗传算法中融入深度搜索、分层结构和禁忌表等机制强化遗传算法寻优能力。然后,利用改进的k-opt方法加速算法局部搜索运行效率和尽量避免算法陷入早熟问题(图3)。

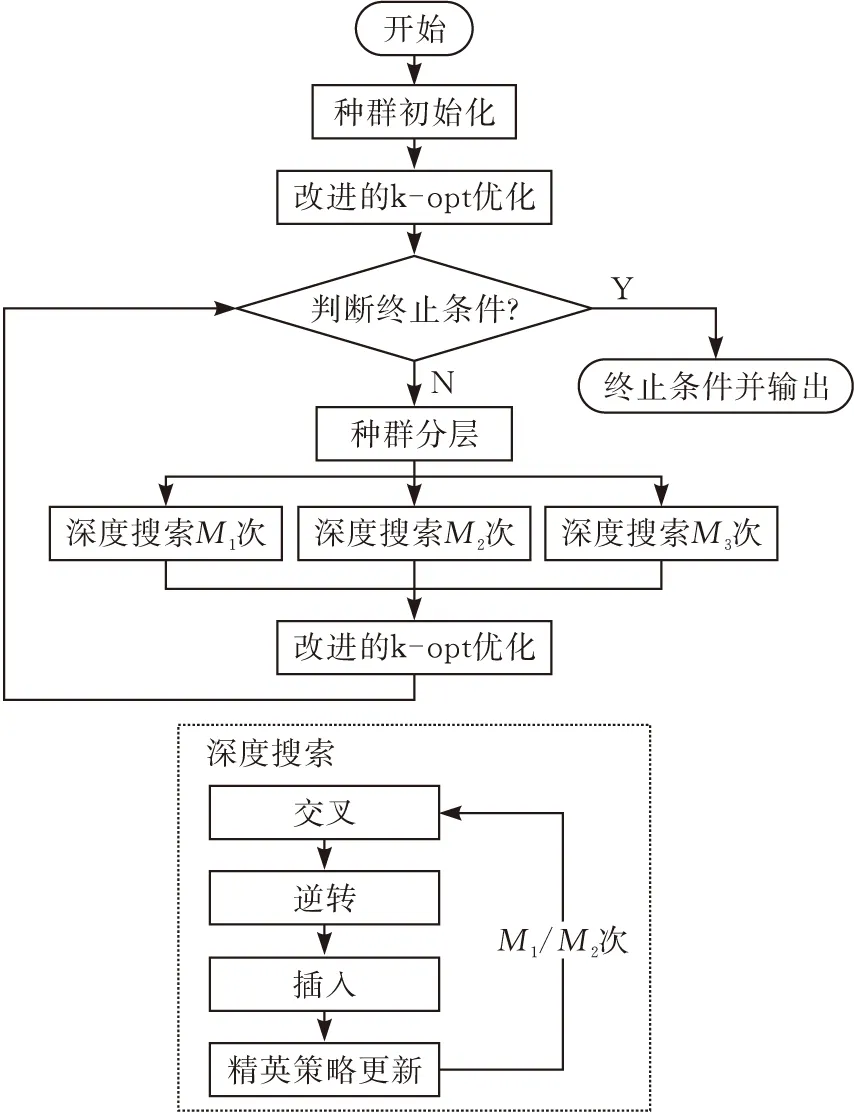
图3 改进的k-opt遗传算法流程

在改进的遗传算法中,首先通过随机编码初始化种群个体,然后以距离作为适应度函数计算不同个体的适应度值。同时,采用改进的k-opt方法初始化,使种群个体获得较优解,加速算法的寻优能力。然后,算法采用交换、逆转和插入三种方式全局搜索。其中,交换是指将有序序列中随机两个节点的位置交换,逆转是指将有序序列中随机一个片段置换方向,插入是指将有序序列中的任意一个节点插入到与自身不相邻的位置。通过上述三种方式,种群个体在全局内随机搜索。同时,融合深度搜索、分层结构和禁忌表三种策略增强遗传算法的搜索能力。

首先,采用基于排序的分层结构(第一层群体、第二层群体和劣质群体)细化种群,该策略启发于灰狼优化算法[16]:

其中,N为城市规模大小,p∈[1,N]且为整数,X(i)表示种群中的第i个个体,通过分层结构将种群分为三个不同的分支。第一层群体包含较优求解方案;第二层群体包含次优求解方案;劣质群体包含拟合效果较差的求解方案。对第一、二层群体进行基于深度搜索的全局探索。即对第一、二层个体分别独立搜索M1、M2次(M1、M2为超参数)。此外,重新初始化劣质群体,增大遗传算法的全局搜索能力。同时采用改进后的k-opt方法快速接近局部较优解。该分层结构使优质个体具有更高的频率被优化,同时也使群体有更大概率搜索到更优方案。最后,采用精英策略保留新生成的优质个体。

超参数M1、M2根据城市规模取两组不同的值。当城市规模不大于100时,降低深度搜索频率;当城市规模大于100时,加大深度搜索频率。其公式如下:

此外,在每次搜索之前随机更换序列起点位置,但不改变城市序列顺序,其目的是动态化调整搜索起点。更进一步,在交换、逆转和插入三种搜索方式中,通过添加禁忌表提升搜索有效性。禁忌表的设计细节如下:

2)对任意种群个体均初始化一个(1,N)零矩阵禁忌表单Tabu,并判断个体相邻节点是否存在于禁忌表中。若其邻域节点存在于禁忌表,将禁忌表单中该节点的位置置1,表示该节点的邻域节点为较理想节点。

3)随机从S(S={1,2,…,N})或禁忌表单Tabu中选择两个节点(x1,x2),节点设计如下:

其中,R是一个随机数且R∈[0,1]。当(x1,x2)来自禁忌表单Tabu时,从Tabu中随机选择两个位置为0的节点;当(x1,x2)来自S时,随机从S中选择两个不相邻的节点。

4 实验和结果分析

实验采用MATLAB2021编程,PC内存为64GB,Intel(R),Core(TM) i7-11800H CPU。为了验证该算法的有效性,实验采用多个公开TSPLIB实例进行测试,并将本算法和原始遗传算法(GA)、离散灰狼优化算法(DGWO)和离散麻雀搜索算法(DSSA)进行对比(表1)。在求解TSP问题的众多算法中,DGWO和DSSA是目前较新颖的工作,DGWO的效果明显强于GA、ACO、PSO等经典算法,而DSSA获得比离散蝙蝠算法[10]和离散青蛙算法[11]更优的处理方案[9]。三种对比算法的超参数均为默认参数。由于算法所采用的种群规模和迭代次数均不一致,为了统一对比,本文所有算法的种群规模均为50,分别对每个实例求解10轮,每轮迭代100次。评价指标为10次运行中的最优求解路径长度Best和算法平均运行时长Time(单位:秒)。在当前公开的最优路径长度数据中,均只保留到整数,因此本实验中的最优求解路径长度也采用向下取整的方式保留到整数位。此外,计算不同算法最优求解路径长度和TSPLIB提供方案的差异,得到两者偏差的百分比Gap(单位:%)。

其中,Best表示算法最优求解路径长度,S0表示TSPLIB公开的最优方案。指标Gap反映算法逼近最优解的能力,其值越小越好。

表1为不同算法求解结果。与其他三种对比算法相比,本文提出的算法总体上获得了更好的解决方案。在30个TSPLIB实例中,本文算法获得26个更优的解决方案;在pr107和u159实例上,本文算法获得比TSPLIB提供的方案更好的处理结果;四种算法的平均偏差比为: GapGA∶GapDGWO∶GapDSSA∶GapOurs=3.788∶1.539∶1.447∶1,本文算法提供的方案在指标Gap中获得了更低的偏差率,更接近公开方案。此外,在运行效率上本文算法也同样优于其他三个算法。四种算法的平均运行时长比为:TimeGA∶TimeDGWO∶TimeDSSA∶TimeOurs=3.914∶16.897∶5.068∶1,在求解问题效率上,本文算法得到大幅提升,即验证了改进k-opt方法的有效性,且原始遗传算法在效率上优于两种新型算法。图4～图6展示了部分实例在本算法上求解的最优方案,观察发现明显不存在路径交叉的现象。

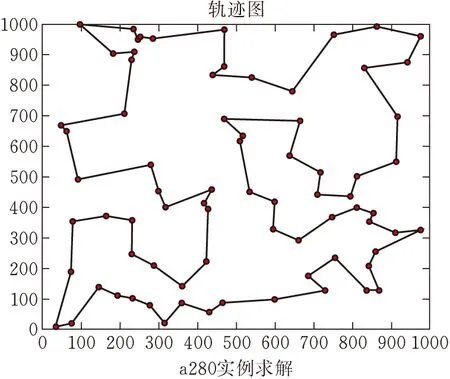
图4 a280最优路线

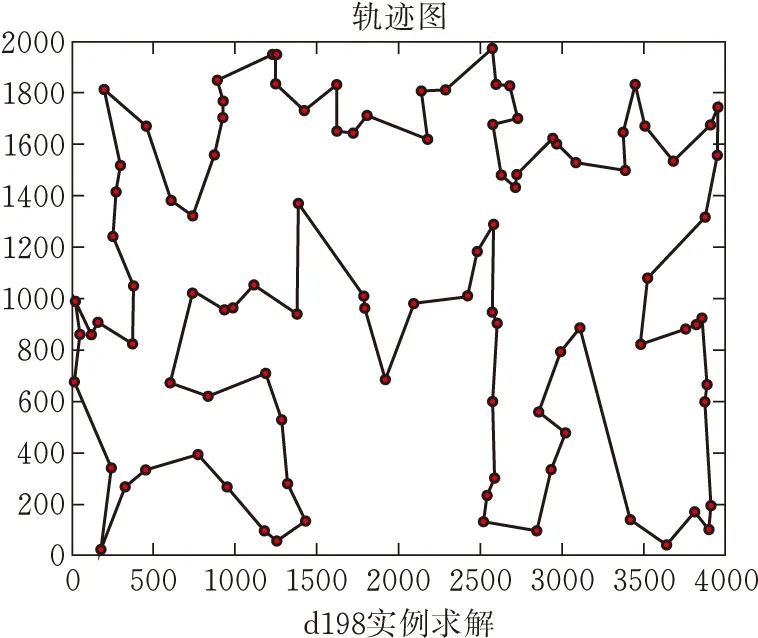
图5 d198最优路线

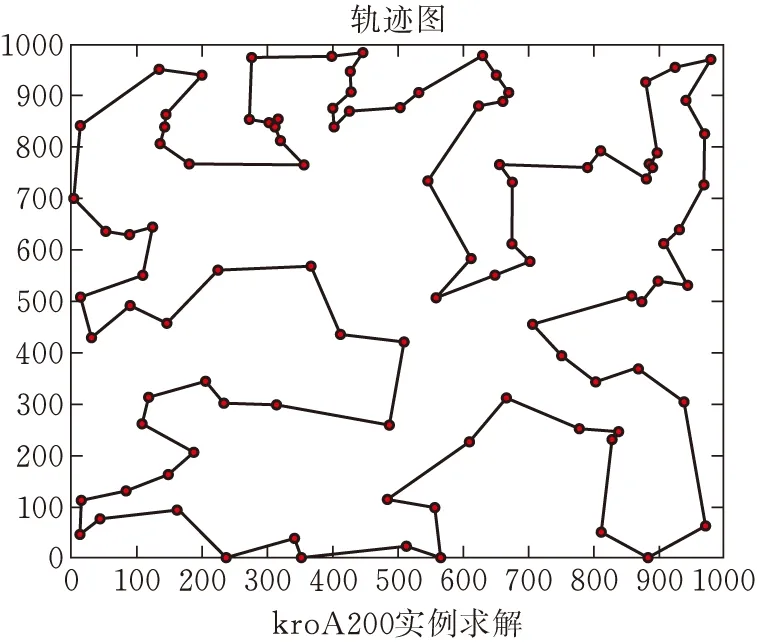
图6 kroA200最优路线

图7～图9为四种算法在三个实例上的迭代收敛曲线。以图7中a280实例拟合曲线为例,通过对比四个算法的拟合曲线发现,原始遗传算法存在早熟问题,即算法过快收敛于局部最优解;而改进的算法即使在中期仍然能搜索出更优解。同时,改进的遗传算法前期强化种群全局搜索能力,后期加强种群局部搜索能力,故在整个搜索过程中能较好地平衡算法的探索和开发能力。与DGWO和DSSA相比,本文算法的前期寻优能力存在微弱的差距,但整体寻优能力存在优势。其根本原因在于:本文通过改进k-opt方法在前期增强算法探索能力,同时结合多种策略在当前解基础上添加扰动因子,在提高算法求解质量的同时能加快算法运行效率。

图7 d198迭代收敛曲线

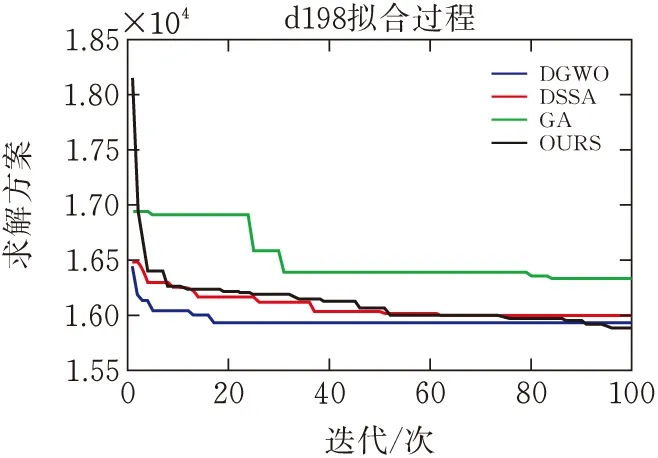
图8 a280迭代收敛曲线

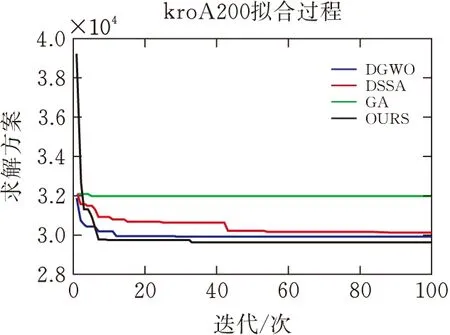
图9 kroA200迭代收敛曲线

在上述对比实验的基础上,本文将原始2-opt方法和改进的2-opt方法进行对比。两种不同方法均采用改进的遗传算法作为基本框架,指标为10次运行中的最优求解路径长度Best、算法最优求解路径长度和TSPLIB提供方案的差异Gap、10次平均求解路径长度Avg、10次最优方案的方差Std和算法平均运行时长Time(单位:s)。实验在14个小型实例数据上进行测试,其他参数均采用上述方案。分析求解结果,在指标Best中,两个不同方法在7个实例上获得相同的最佳求解方案,原始2-opt方法获得3个更优的方案,改进的2-opt方法获得4个更优的方案;在指标Avg和指标Std中,原始2-opt方法分别获得6个更优的方案,改进的2-opt方法分别获得7个更优的方案;在指标Time中,改进的2-opt方法明显消耗更少的时间求解问题, 两种方法的平均效率为Time2-opt∶ Time2-optimproved)=11.3 ∶ 1。综上所述,改进后的2-opt方法既降低了算法时间复杂度,也减缓了原始2-opt算法过早陷入局部最优解问题。

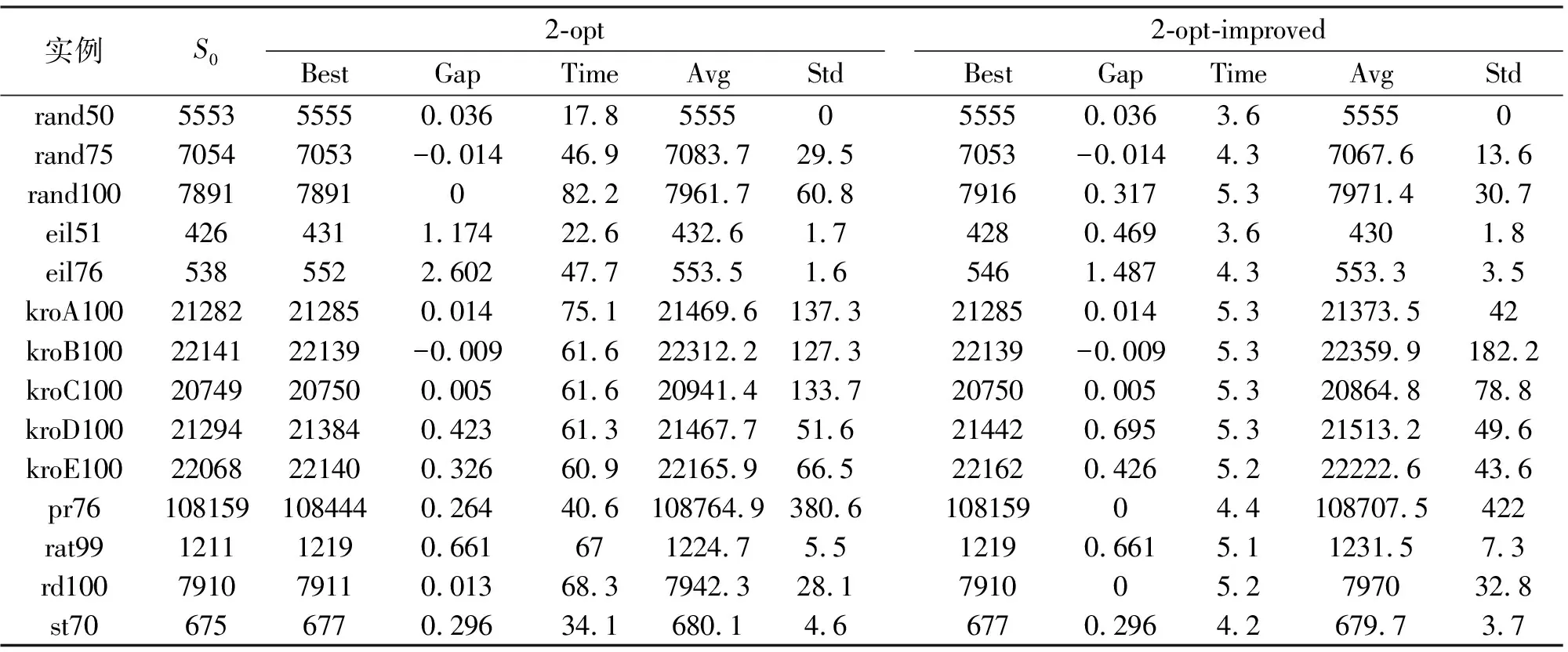
表2 原始k-opt方法及其改进方法对比

5 总结

本文提出一种求解旅行商问题的改进k-opt遗传算法。该算法改进原始遗传算法以增强算法探索能力,同时融合改进的k-opt方法强化局部搜索,既能加速算法运行效率,又能减缓算法陷入局部最优解。具体地,采用交换、逆转和插入三种策略使得种群个体在更广阔的范围搜索;添加禁忌表有效增加搜索;随机置换序列顺序;利用深度搜索和分层结构优化当前解。实验采用多个公开数据集进行测试,通过对比离散灰狼算法(DGWO)、离散麻雀搜索算法(DSSA)和原始遗传算法(GA),该算法在求解TSP问题时收敛精度和收敛效率均有良好的表现。虽然本文在求解TSP问题时获得了较优解和较快运行效率,但将TSP问题迁移到超高规模(如TSP-art)时,该算法的求解方案和已知最优路径还存在一定差距。如何在超高规模问题中求解TSP问题将成为下一阶段的研究目标。