LCL型SAPF的并联复合电流控制策略

伍 科,蒋云昊,卜健怡,樊 超,邓 伟,徐岸非,袁 雷

(1 湖北工业大学太阳能高效利用及储能运行控制湖北省重点实验室, 湖北 武汉 430068;2 襄阳湖北工业大学产业研究院, 湖北 襄阳 441100;3 中建三局第二建设工程有限责任公司, 湖北 武汉 430068)

并联型有源电力滤波器(shunt active power filter,SAPF)作为一种可动态补偿谐波的设备,能很好抑制电流型谐波污染,受到广泛的关注和探讨[1-2]。LCL滤波器因其较小的体积和良好的性能得到了广泛的应用[3],为了补偿谐波电流,学者们设计了众多电流控制方案[4-5],其中最为常用的电流控制器方案是PI控制方式[6],可以对直流信号无静差跟踪,但系统稳定裕度不高,谐波补偿能力不佳。文献[7]采用模糊PI控制器前馈的方式与重复控制器结合,提升了系统的动态响应速度和稳态补偿精度,但重复控制器的内核所需存储单元较大,系统动态响应性能较差。

针对LCL型有源电力滤波器,本文提出了一种模糊PI控制器和快速重复控制器并联的复合控制策略,通过模糊PI控制器实时改变参数应对变化的谐波指令信号,提升系统动态响应能力,快速重复控制则针对6k±1次谐波具有高精度跟踪性能,同时可以缩短固有延迟的周期,实现高精度补偿谐波电流的性能。最后,通过仿真验证了该策略补偿谐波电流的有效性。

1 LCL型SAPF的数学模型及谐波电流分析

图1为LCL型SAPF的系统结构框图。us为三相电网电压,L1为SAPF逆变器侧电感,L2为SAPF电网侧电感,C是滤波电容,R是无源阻尼电阻,非线性负载由三相不控整流桥、RL和LL构成。通过控制使得SAPF输出补偿电流i2与负载中的谐波电流大小一致,相位相反,与负载电流iL中的谐波电流相互抵消,电网的电流is的波形近似于标准的正弦波,从而实现补偿谐波的效果。

图1 LCL型SAPF的系统结构框图

1.1 LCL型SAPF数学模型

在三相对称电路中,可以只分析单相模型,图2为SAPF的单相等效电路。其中,us是电网侧电压,uinv是逆变器侧输出电压,uc是电容两端电压,ic是电容支路的电流,i1和i2分别是LCL滤波器逆变器侧和电网侧电流。

图2 单相等效电路

由图2可得:

(1)

由式(1)得到从逆变器输出电压uinv到电网侧电流i2的传递函数

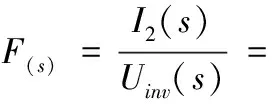
(2)

1.2 谐波电流分析

采用瞬时无功理论提取负载电流iL中的谐波电流成分,从abc坐标系到dq坐标系的变换矩阵

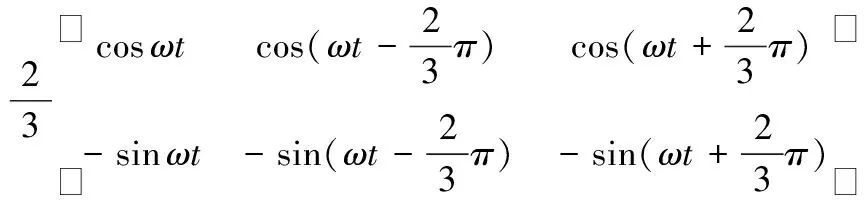
(3)

式中ω是电网基波频率。

负载电流iL由基波电流和不同的各次谐波电流分量组成,如式(4)所示,Im为基波的有效值,In为谐波的有效值,n=6k-1和n=6k+1为基波频率倍数,分别表示负序谐波和正序谐波,φm、φm-和φm+φm分别表示A相基波相位、正序谐波相位和负序谐波相位。

(4)

通过式(3)变换到dq坐标系可得:

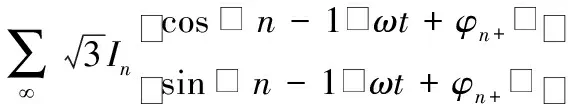
负载电流经过abc-dq坐标系变换后,这些6k±1次的特征谐波电流信号将转换为对应的6k次谐波电流信号。

2 快速重复控制策略设计

PI控制在非线性系统中跟踪高频谐波信号能力较差,无法保证系统的补偿精度,而重复控制能够较好地抑制周期性扰动造成的电流畸变,实现稳态无静差地跟踪高频谐波信号,但本身存在延迟环节,动态响应慢,需加强动态性能方面的改善。

2.1 传统的重复控制

传统重复控制器内模结构见图3,其内模部分的传递函数为:

式中:N=fc/f0,其中fc为采样频率,f0为基波频率,Q(z)为衰减滤波器,通常小于1。

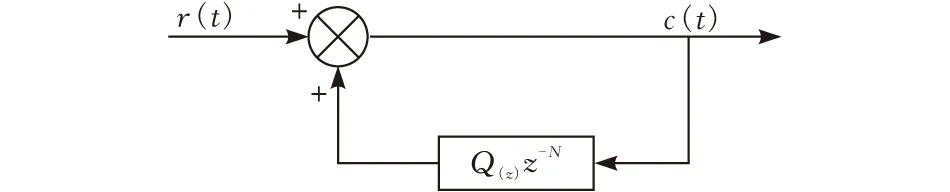
图3 传统重复控制器内膜结构

传统重复控制器的频率特性如图4所示,从频率特性图可以看出传统重复控制器对各个频率均具有高增益,实现对谐波信号的无静差跟踪。但在实际应用中,由于延迟环节使重复控制在运行中存在一个基波周期的延迟,当非线性负载变化后,会产生较大幅度的波动,从而影响SAPF对谐波电流的补偿效果。

2.2 快速重复控制设计

三相六脉冲整流器装置中,谐波电流中的主要成分为6k±1(k=1,2,3,…)次特征谐波,且负载电流的奇次谐波经过abc-dq坐标系变换后为偶次谐波的特性。本文提出一种快速重复控制器,该控制器内膜可针对性补偿6k±1次谐波。从延迟环节的阶数可以看出,延迟环节阶数的降低使得运行时所占内存变小,减少了运算量。快速重复控制器的内模结构如图5所示,其传递函数如式(7)所示。

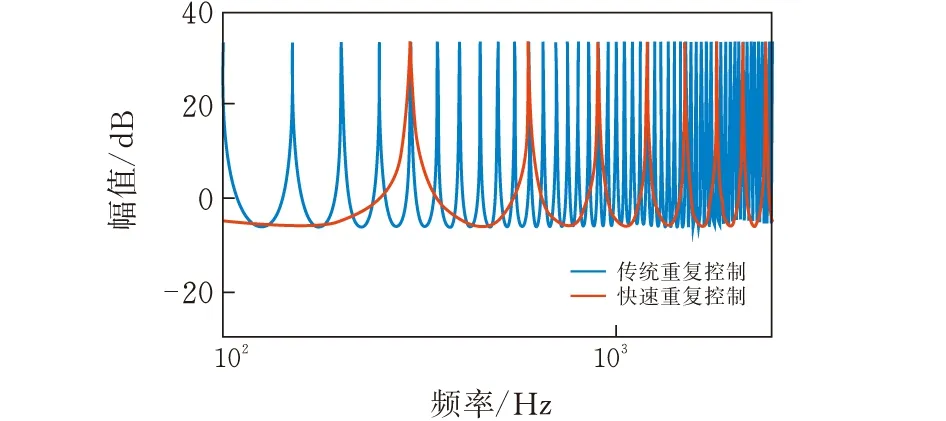
图4 不同重复控制器的频率特性图对比

(5)

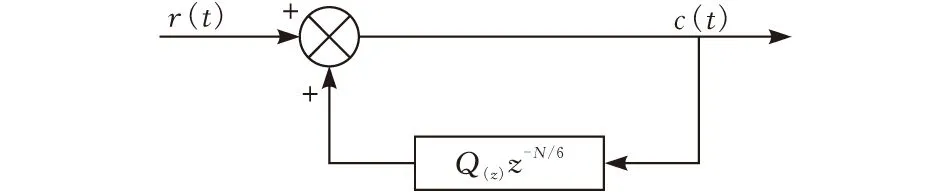
图5 快速重复控制器内膜结构

快速重复控制器的内膜伯德见图5,该控制方法在6 k×50 Hz处同样具有高增益,可以有效地补偿非线性负载造成的特征谐波电流,而在非6 k×50 Hz的其他频率处不再具有谐振高增益,有效避免了放大其他次数谐波的幅值,实现零稳态误差的补偿6 k次谐波,提高了快速重复控制器的稳态性能。

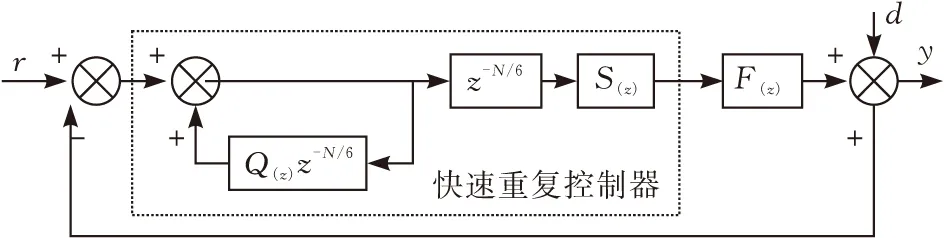
图6 快速重复控制器结构

如图6为本文设计的快速重复控制器结构框图,本文选用电网侧电感电流作为电流反馈量,衰减滤波器Q(z)通常小于1[8],本文Q(z)选取工程经验值0.95。由于等效被控对象LCL滤波器存在固有谐振的不稳定因素和系统相位滞后的情况,需针对被控对象设计补偿矫正器S(z),从而实现系统零相移零增益的特性,补偿矫正器传递函数如下:

S(z)=zkH1(z)H2(z)

式中:zk为超前环节;H1(z)为二阶低通滤波器;H2(z)为零相移谐波器。

设计二阶低通滤波器的传递函数

式中,穿越频率ωn=2π·3750rad/s,阻尼系数ξ=0.8。采用双线性变换,则该二阶低通滤波器的离散域传递函数为:

选择梳状滤波器作为陷波器,抑制谐振峰值,其离散传递函数

将参数L1=1.3 mH,L2=0.2 mH,C= 10 uF,Rd=0.03 Ω带入式(2)可得离散域中被控对象的传递函数

绘制k取不同值时S(z)F(z)的相频特性曲线(图7)。

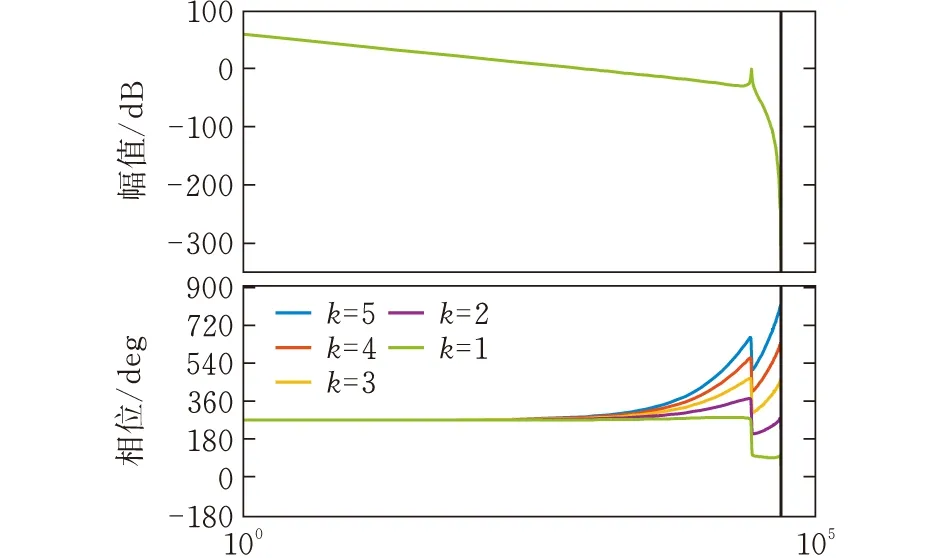
图7 不同k值时S(z) F(z)的相频特性曲线

由图7知,当k取2时,效果最好,能有效抑制谐振频率的谐振峰,经过陷波器的陷波频率附近,幅值迅速衰减,在其他频率处无幅值衰减,并不会引起相位滞后,可保持较小的稳态误差,高频段时,有一定的相位偏差,但信号的增益有较大的衰减,即相位偏差不会对系统的稳定性产生影响,本文选取k的值为2。

3 模糊PI控制策略

有源电力滤波器控制的原理一般是把参考电流信号与SAPF输出电流进行对比得到指令电流信号,经过电流控制器实时跟随指令电流信号的变化,最后通过SVPWM调制得到脉冲信号控制逆变器输出补偿电流。传统的电流控制器采用的是PI控制器,对数学模型的精准度要求高,很难适应不同的谐波指令信号,模糊PI控制器则可实现对参数的自调整[9]。

3.1 模糊PI控制器

PI控制器的增益通常用不同的方法和系统的数学模型来确定,这些控制器的性能易受系统阻抗和负载动态变化等因素的影响。因此,本文采用模糊PI控制,该控制器可实时调整参数以适应负载的变化。

图8为模糊PI控制器等效框图,电网侧电感电流通过负反馈与谐波指令对比,将误差送入模糊PI控制器。模糊PI控制器的参数可以通过独立于系统参数的模糊规则获得。在该控制器中,根据模糊控制规则输入PI控制器的增益ΔKP和ΔKI,达到实时调节KP和KI参数的目的。图9显示了采用模糊PI控制的内环控制器的框图。PI控制器的ΔKP和ΔKI增益由两个输入、两个输出的模糊规则确定。

图8 模糊PI控制器等效框图

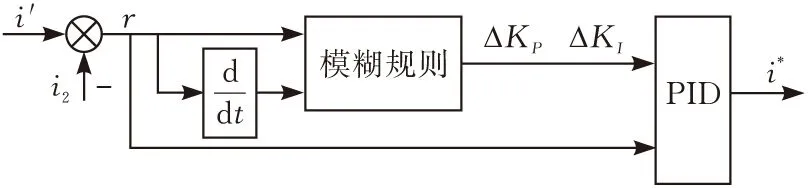
图9 带模糊增益调节的PI控制器

3.2 模糊集的建立

模糊控制器的输入量为偏差r和偏差率Δr,输出量为PI控制器的参数的增益ΔKP和ΔKI。将系统输出偏差r和输出偏差率Δr变化范围定义为模糊集上的论域:

r,Δr={-6,-4,-2,0,2,4,6}

其模糊集为{NB,NM,NS,ZE,PS,PM,PB},它们分别代表负大、负中、负小、零、正小、正中、正大。确定PI控制器的参数的隶属度函数,定义它们的模糊论域为:

ΔKP={-0.6,-0.4,-0.2,0,0.2,0.4,0.6}

ΔKI={-3,-2,-1,0,1,2,3}

其模糊集定义为{NB,NM,NS,ZE,PS,PM,PB},分别代表负大,负中,负小,零,正小,正中,正大。

3.3 模糊规则的建立

模糊控制规则类似人类的判断思维,根据专家的经验和知识结合多次操作的经验和数据分析,设计出以下模糊规则,如表1和表2所示。

表2 ΔKI模糊推理规则

3.4 模糊控制的精确化

精确化计算是把语言表达的模糊量回归到精确的数值,经过模糊规则处理,输出得到ΔKP和ΔKI的对应隶属度。采用重心法进行精确化的计算,就可得出KP和KI的修正值,其调整如下式:

KP=KP0+ΔKP,KI=KI0+ΔKI

式中KP0、KI0表示常规PI控制器的初始参数。

4 复合控制设计

为进一步提升系统的动态响应性及稳定性, 将模糊PI控制器与快速重复控制器通过并联的连接方式作用于受控对象, 系统控制结构如图10所示。

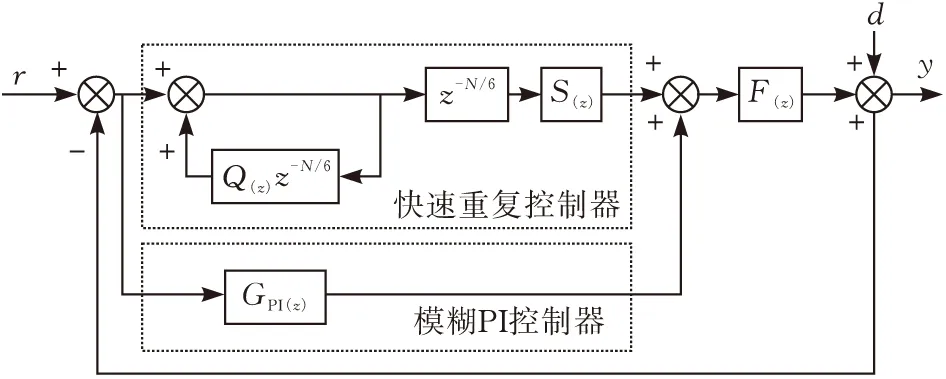
图10 系统复合控制结构图

由图10可得整个系统的传递函数为:

式中,GFRES(z)表示本文快速重复控制器,GPI(z)表示模糊PI控制器,令分母为0,得到控制系统的特征方程为:

Δ1Δ2=0

Δ1为仅含 PI 控制时的特征方程,Δ2为快速重复控制器作用时系统特征方程。 因此只有当两者均位于单位圆时, 该复合控制系统才处于稳定状态。 绘制复合控制系统稳定充分条件的轨迹见图11、12。

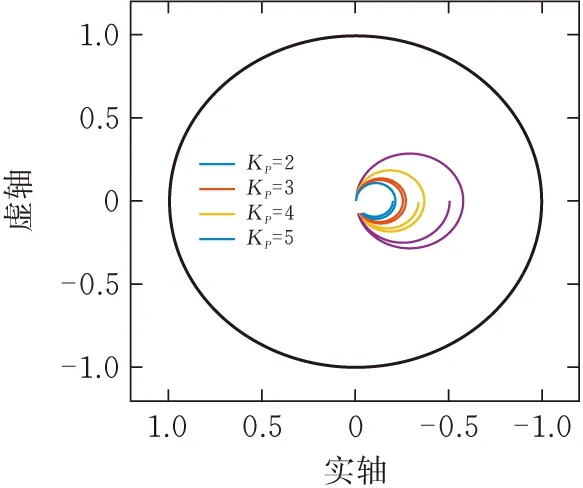
图11 Δ1轨迹

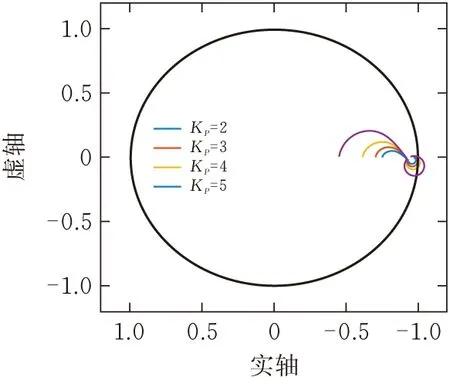
图12 Δ2轨迹

比较图11和图12中的轨迹图可知,KP=2和KP=3时,系统处于稳定状态。在系统处于稳定状态的同时,需要尽量选取较大的KP使系统启动时具有较快的响应速度,由此可以得到模糊PI控制的初始参数,令Kp0=4,Ki0=20。

5 逆变器侧直流电容电压控制策略

逆变器侧直流电容电压的稳定直接影响到了有源电力滤波器的补偿精度,传统PI控制的方法可有效地确保直流电容稳压的精确度[10],但该方式的快速性仍然存在缺陷,在负载突变时不能够快速响应,系统达到稳态费时较长。将模糊PI控制方式应用于该逆变器侧直流电容电压的控制方式上,控制规则见表1、表2,将误差r误差率Δr送入模糊推理机,得到PI控制器的参数的增益ΔKP和ΔKI,在通过模糊精确化得到准确的PI控制器参数,达到实时修正PI控制参数的目的,以提高系统的快速性和精确性,设置逆变器侧直流电容电压常规PI控制器的初始参数Kpu0=6,Kiu0=20 。

6 仿真验证

基于上述理论分析,在MATLAB/Simulink平台搭建仿真模型。具体参数为:三相电网线电压有效值为380 V;频率50 Hz;三相不控整流器由RL=10 Ω电阻和LL=20 mH电感串联作为非线性负载,在0.3 s时并联一个相同阻感的负载;SAPF直流电容电压参考值为800 V;储能电容开始电压为650 V;SAPF输出滤波器L1=1.3 mH,L2=0.2 mH,C= 10 uF,Rd=0.03 Ω;开关频率为10 200 Hz。

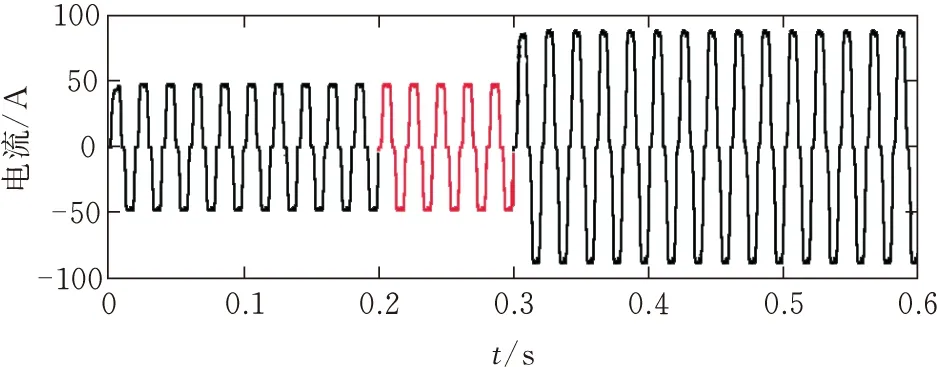
图13 负载侧A相电网电流波形

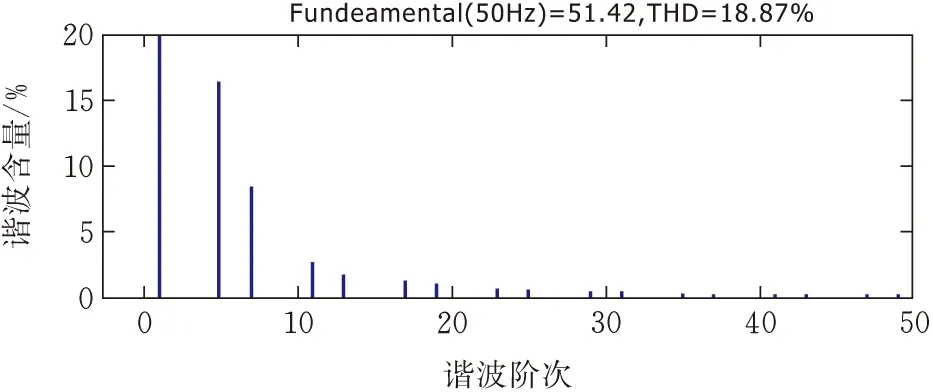
图14 负载侧A相电网电流频谱

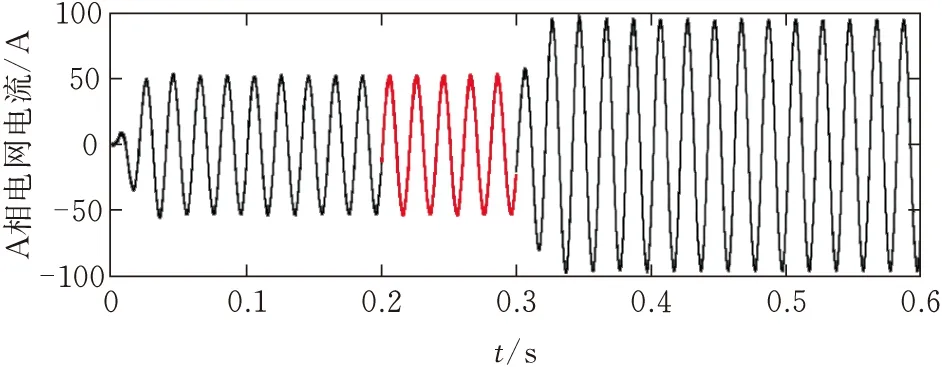
图15 PI+重复控制并联时A相电流波形

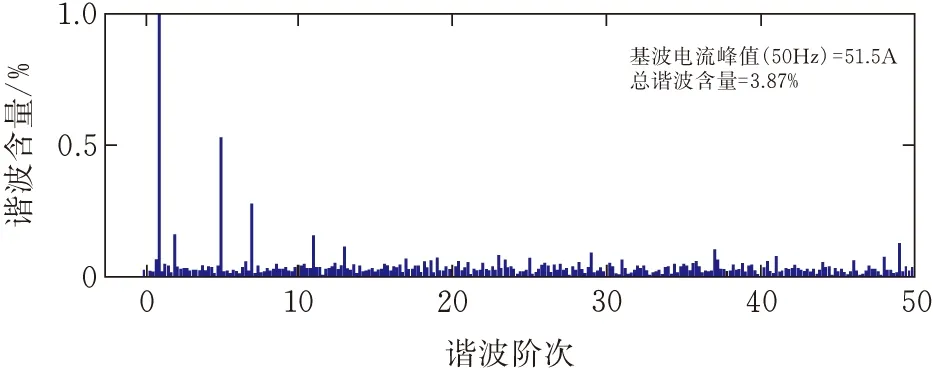
图16 PI+重复控制并联时A相电流FFT分析

如图17和图18所示,为本文设计模糊PI+快速重复控制并联补偿后的A相电网电流波形及其电流频谱,在SAPF补偿谐波电网电流后,A相电网电流近似正弦波,电网电流畸变率由18.87%降低到1.81% ,符合电能质量标准。

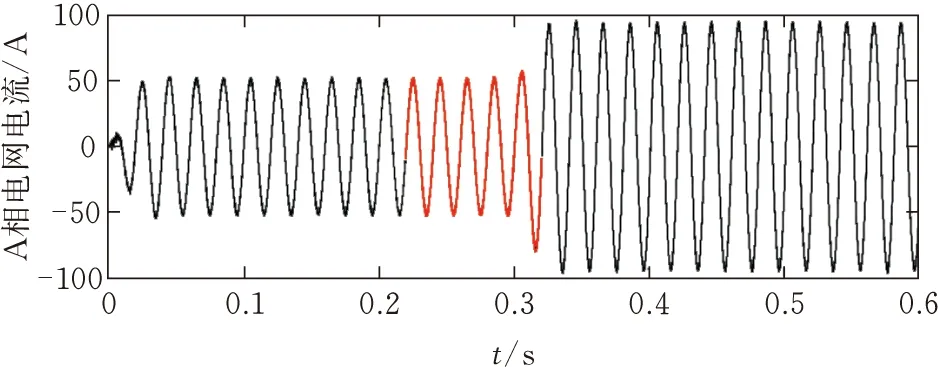
图17 模糊PI+快速重复并联控制A相电流波形

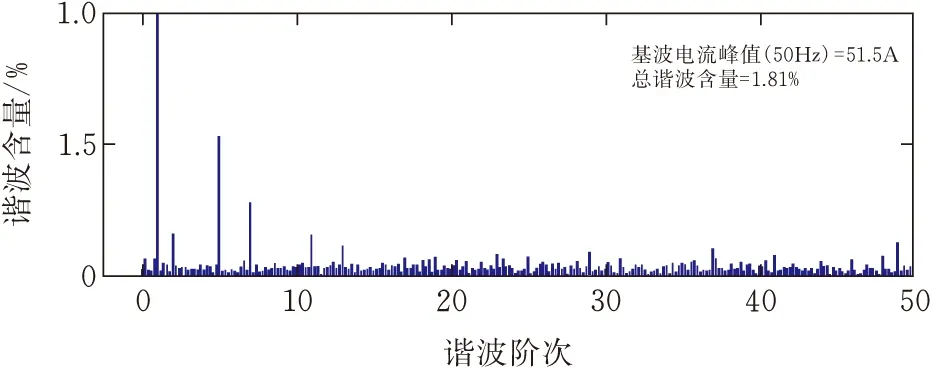
图18 模糊PI+快速重复并联控制A相电流FFT分析

对比图16和图18的电流频谱分析,该控制方式相较于传统PI+重复控制方式,电流畸变率下降了2.06%,由于快速重复控制的作用,针对6k±1次特征谐波电流的补偿效果更好,并且有效避免了放大其他次数的谐波电流,而模糊PI控制则使系统具有更快的响应速度和稳态时的补偿精度,使补偿后系统的总谐波含量更低。由图17可知,本文提出的控制策略在0.3 s负载突变的情况下,可以快速跟踪并有效补偿谐波电流,从而实现对电能质量的改善。仿真结果验证了该复合电流控制方案可以快速响应负载的变化,补偿电网谐波电流(图19),在稳态时具有较高的稳态补偿精度。如图20所示,由于延迟环节的影响,逆变器侧直流电容电压的控制在第一周期并未对电容充能,导致电压有一定程度的下跌,在一周期后,模糊PI控制起作用,因模糊PI控制器初始参数较大和电流控制环的影响,电压会先超出800 V并有一定幅值的波动,最后达到稳定值,模糊PI控制策略仅用了约0.02 s就达到了电压稳定,相较于常规的PI控制策略,快了约0.015 s,在0.3 s负载突变后,模糊PI控制策略仅用了约0.016 s重新达到稳定状态,比常规的PI控制策略快了约0.014 s,有效提升了系统的响应速度。

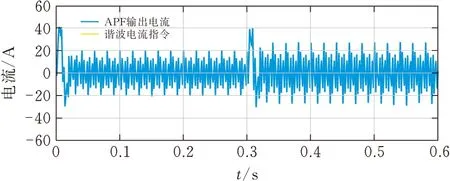
图19 谐波电流跟踪状况

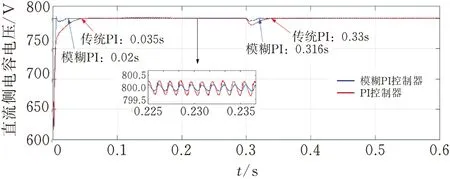
图20 不同控制器逆变器侧直流电容电压波形

7 总结

本文提出了一种基于模糊PI结合快速重复控制的LCL型有源电力滤波器并联型复合电流控制策略,采用该策略可有效补偿电网谐波电流,提高稳态补偿精度且具有良好的动态性能。系统仿真表明:

1)电网电流的THD含量由传统的PI+重复控制策略的3.87%降为改进型复合电流控制策略的1.81%,表明该控制策略能较好地补偿电网谐波电流,稳态补偿精度较高;

2)快速重复控制器和模糊PI控制器并联结合的方式能够有效地提升SAPF补偿谐波电流的动态响应速度,在快速重复控制器作用之后减小SAPF实际输出补偿电流与电流指令信号的偏差;

3)快速重复控制仅在6k±1次谐波频率处具有高增益,参与补偿后有效地降低了该频率处的谐波含量,可应用于三相整流器等电力电子装置;

4)逆变器侧直流电容电压采用模糊PI控制策略后,响应速度和精确度都有进一步提高。