水电站一次控制系统和稳定性分析

杨 弓

（国能德宏发电有限公司，云南 德宏 679300）

0 引言

本文工作涉及水电站及其基本设备的运行和控制，并对实际水电站的动态行为进行了分析，主要目标是使用基于微分方程的非线性模型对实际电厂进行建模。该模型的参数可以很容易地从现场测试中获得，并研究处于孤立运行中的电厂的主控制系统，以便为所选控制器定义最佳参数[1,2]。发电厂有特殊的控制系统，以确保稳定运行。电力系统的稳定运行需要频率控制，当系统承受显著的负载变化时，频率控制将其保持在可接受的范围。由于频率对所有系统都是通用的，因而某一点的有功功率变化将作为频率变化反映在系统上。

主控制系统由速度传感器、控制器、执行器和液压供应系统组成，其主要功能是保持角速度恒定并等于其标称值，并在负载变化或操作条件变化时改变分配器位置。每个操作条件都有其要求，因此适合一个条件的控制器参数可能不适合另一个条件。自适应控制的使用是满足不同操作条件的一种最佳选择。定义控制器参数的通常是考虑施加最严格操作要求的前提条件，并保证在这种情况下保持稳定性。

1 技术方法分析

水电站一次控制系统主要由水轮机、调速装置、发电机、电力系统等组成，其目的是保持水电机组的稳定运行，实现电网平衡和负荷调节。稳定性分析是对该控制系统的稳定性进行评估，以保证系统在各种工况下的运行稳定性和安全性。

水电站的一次控制系统具有以下几个关键组成部分：

水轮机。水轮机是水电站的主要动力装置，其转速和负载的变化会直接影响发电机的输出功率和电力系统的稳定性。因此，水轮机的调速性能是保证系统稳定性的重要因素之一。

调速装置。调速装置主要用于控制水轮机转速和负载的变化，以满足发电机输出功率的需要。调速装置需要具备快速而准确的响应能力，能够及时调整水轮机的工作状态，以保持系统的平衡。

发电机。发电机是将水轮机的机械能转化为电能的关键设备。发电机的负荷变化会影响电力系统的电压和频率稳定性，因此发电机的稳定性和调节能力对保证系统稳定运行至关重要。

电力系统。水电站一次控制系统中的电力系统主要包括变压器、开关设备、电缆等。电力系统需要具备稳定的电压和频率，以保证电网负荷的平衡和稳定。

稳定性分析的主要内容包括以下几个方面：静态稳定性分析，通过分析水电站的负荷特性、水轮机的转速-负载特性和发电机的功率-电压特性等，确定系统的静态稳定性。在水电站的设计和运行过程中，需要保证系统在各种负荷条件下的工作点稳定，并且有足够的调节余量。动态稳定性分析，通过对水电站一次控制系统的动态特性进行研究和分析，确定系统对扰动的响应过程和稳定性指标。动态稳定性分析需要考虑系统的动态响应速度、稳定裕度和暂态稳定性等因素，以保证系统在负荷波动等扰动情况下的稳定运行。控制系统设计和仿真，基于稳定性分析的结果，进一步设计和优化水电站一次控制系统的参数和结构，提高系统的稳定性和控制性能。通过仿真模拟和实地测试验证系统的稳定性，确保系统能够满足各种工况下的运行要求。

因此，水电站一次控制系统的稳定性分析是保证系统安全稳定运行的重要手段之一。通过对系统的静态稳定性和动态特性进行分析和评估，并进行相应的控制系统设计和优化，可以有效提高系统的稳定性和可靠性，保障水电站的生产和运行安全。

2 数学模型分析

2.1 水压回路及设备

该模型基于这样一种假设：即水是不可压缩的流体，压力钢管是刚性的。介绍了两种类型的厂房：单个压力钢管厂和带有公共管道的多个压力钢管厂。

单个压力钢管厂有一条管道为每个水轮机供电。根据能量定律，压力管道中的流量变化率为

在这些方程中，h0是水柱的静压（N）；hL是水轮机入口的压力（N）；hf是摩擦压力损失（N）；g 是重力（m/s2）；A 是导管的横截面（m2）；l 是导管的长度（m）；q 是流速（m3/s）；f 是导管的损失系数[3-5]。

水电站启动时间定义为

带有公共导管的多个压力钢管，根据所给出的方程，压力钢管中的流量变化率为

其中，hoc是分叉处水柱的静压（N）；hc是分叉处的压力（N）；hfc是公共管道上的摩擦损失（N）；Twc是根据方程（4）的公共管道的水启动时间常数（s）；qc是公共管道中的流速（m3/s）；qi是单个压力管道中的流量（m3/s）。

水电站稳定性研究的基本设备是水轮机和发电机，用以下数学模型代表。

闸门位置（Y）和主控制系统信号之间的关系

其中，T1和T2是电机的时间常数。

涡轮水轮机可以通过其阀门特性来建模

G 被定义为

其中，y 为闸门位置（标称位置为y=1，关闭位置为y=0），Tg为闸门时间常数。这项工作中的门时间常数被认为是1.0s。

发电机机械功率（Pm）和电功率（Pe）的值之间的差导致轴扭矩的变化，该变化产生角速度变化。如果将常数H 定义为

其中，J 是发电机惯性（kg.m2）；ω0是标称速度（Hz）；SN 是标称视在功率（V.A.）；可以写为

电功率可以写成负载功率（PG）的函数

2.2 控制系统

本工作中研究的4 个控制器。其中，传统控制器具有以下传递函数

其中，r 是瞬态下降；Tr是控制器零参数。

比例积分，该控制器的传递函数如下

其中，T1是积分常数。

比例积分和比例导数。该控制器是比例积分控制器和比例微分控制器的组合。

比例积分和导数。该控制器具有以下传递函数

3 实例分析

3.1 实际水电站的现场试验结果

大盈江一级电站水轮机为立轴混流式水轮机，金属蜗壳，转轮公称直径3050mm。本机包括水轮机本体和辅助设备两大部分，本体部分分为埋入部分，导水机构，转动部分，主轴密封，φ950 油导轴承，调速机构，管路布置，仪表架装配和工具部分，辅助设备有φ4400 阀门，WT-80调速器（调速器运行规程单独编写），自动化元件等。水轮机部分参数见表1。

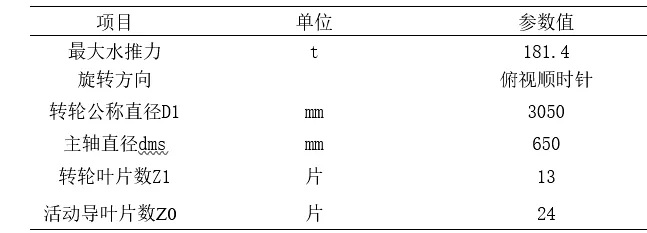
表1 水轮机部分参数Table 1 Partial parameters of hydraulic turbine

表2 水压回路Table 2 Water pressure circuit

对该模型进行了评估和参数计算。图2 显示了系统主界面信息，在主信息界面上可以方便地查询直流系统的实时数据、设置运行参数，主界面从上到下分为5 部分。

第一部分包括图中的1 ～4 号按钮，用于设置参数、查询告警信息及显示帮助信息；第二部分包括图中的5 号按钮，用于查询交流输入信息；第三部分包括图中的6 号按钮，用于查询整流模块信息；第四部分包括图中的7 ～12号按钮，用于查询直流母线上的各种设备信息，如蓄电池、合闸母线、控制母线、逆变模块、DC-DC、绝缘监测仪等设备信息，16 号按钮，用于查询交流屏实时数据信息；第五部分为状态栏（标号13 ～15）。显示系统运行状态、电池状态以及时间等信息。

当 上 游 水 位（hM） 为79.2m， 下 游 水 位（hJ） 为33.7m ～31.8m 时。因此，净水头大约在49.4m ～54.5m 之间变化。发电机的惯性为600t。

净水头的计算公式为

稳定性研究是基于接近最佳条件的操作范围进行的，以50 的净水头为例，表3 为运行条件。闸门打开时间为9.4s。

将一台水轮机运行条件下不同闸门位置的模型结果与现场结果进行了比较，偏差非常低，从-0.54%～0.76%不等，见表4。这些结果被认为是符合条件的，验证了该水电站的模型正确性。

表4 与实际结果相比的模型偏差Table 4 Model deviations compared to actual results

3.2 主控系统验证

研究的控制器有传统控制器、PI 控制器、PID 控制器和PI-PD 控制器。为了比较它们的性能并确定最佳参数，引入了一个性能指标来评估系统在10s 内承受由0.779pu ～1.009pu 的斜坡表示的负载变化时的速度偏差。还要求，当系统承受负载变化时，速度变化的第3 个峰值不高于斜坡的5.0%或第一个峰值的25%。永久下垂被认为是恒定的等于5%。性能指标被定义为

传统控制，所研究的值的范围是Tr在0.5 ～2.5 之间变化，r在1.0 ～20 之间变化。在此范围内计算的性能指数表明，两个参数越低，指数越高。对于Tr=0.5 和r=1.0 m，性能指数的较低值为Ip=0.664，如图1 所示。

图1 作为Tr和r函数的性能指标——传统控制器Fig.1 As a performance indicator for Tr and r functions - traditional controller

PI 控制，P 从0 ～20 变化，I 从0 ～40 变化，对比例（P=Kc）和积分（I=Kc/Ti）增益进行了评估，PI 控制器的性能指标的较低值为Ip=0.456，对应于P=4.0 和I=40.0。在图2 中，表面显示，对于积分参数的较高值，当这些值从0 ～25 变化时，指数显著降低。然而，对于高于25 的值，降低并不显著，并且验证了对于高于40 的值，系统性能不再受到该参数的影响。此外，对于积分参数的低值，比例参数的高值会降低性能指标。另一方面，对于积分参数的高值，比例增益不会显著影响系统的性能。

图2 作为P和I性能指标–PI控制器的函数Fig.2 As a function of P and I performance indicators - PI controller

对于PID 控制器，比例增益（P ＝Kc）在0 ～20 之间变化，积分（I ＝Kc/Ti）在0 ～40 之间变化，导数（D＝Kc.TD）在0 ～20 之间变化。最佳性能指标为Ip=0.457，当P=2.0，I=40，e D=1.0 时获得，如图3 所示。

图3 性能指标作为D和I的函数——PID控制器Fig.3 Performance indicators as functions of D and I - PID controller

在PI-PD 控制系统中，P1 被认为是1.0，可调参数为P2从0 ～20 变 化，I 从0 ～40 变 化，D 从0 ～15 变 化。图4 中的结果表明，对于较高的D 值，系统的性能指标较低。对于超过D=15 的值，响应过于振荡，无法实现稳定性。对于P1=1.0，D=15，P2=5.0 和I=40，指数的最小值为Ip=0.657。

图4 性能指数作为P2及I的函数–PI-PD控制器Fig.4 Performance index as a function of P2 and I - PI-PD controller

在分析了每个控制器的可调参数的不同值后，最佳系统性能见表5。PI 控制器的性能指标越低，传统控制器的性能指数越高。

表5 性能指标的最优值Table 5 Optimal values of performance indicators

图5 显示，对于所有控制器，系统在大约50s 内变得稳定。传统控制器的响应是最具振荡性的，并且呈现出-0.07pu 的较高初始峰值。PI 和PID 控制器的响应非常接近，它们呈现-0.68pu 的初始峰值，并且是阻尼的并且不振荡。PI-PD 控制器也具有不太振荡的响应，但是系统缓慢稳定并且具有0.60pu 的初始峰值。

图5 当系统处于斜坡∆PG=+0.23pu时控制器的比较Fig.5 Comparison of controllers when the system is on a slope ∆PG=+0.23pu

4 结论

本文工作将非线性模型分析与主控制优化相结合，实现了主要目标，即模型的验证和最佳参数的定义。该模型的结果及其参数是根据使用一台水轮机运行的实际水电站计算得出的，符合实际现场要求，目前的流量、功率和速度偏差低于1.0%，这些偏差是由于模型参数的近似值导致。分析表明，PI 控制器的性能指标最好（Ip=0.456），而传统控制器的性能最差（Ip=0.664）。对于实际需求曲线，最优PI 控制器的模型响应在这类水电站的稳定性标准范围内，机械功率遵循需求功率。本文研究成果可以很好地运用到水电站的实际运行当中，具有普遍性。