触发式远程制导火箭弹对单目标射击效率评定*

于远鹏，李臣明

（陆军炮兵防空兵学院南京校区，南京 211132）

0 引言

远程制导火箭作为高精度、高价值火力打击装备，如何采用优化的射击方案充分发挥其作战效能，提高作战效费比，是指挥员决策所关注的问题。制导火箭的射击效率在选择作战力量或射击方案中起到决定性作用。

在传统的炮兵射击理论中已有较为成熟的射击效率评定理论，孙丽君阐述了基于灰理论的弹药毁伤效能计算方法［7］，指出了弹药毁伤效能是受时间、作战环境、弹药消耗量、气候等未知变量的函数并通过数学建模和精度检验得出了较为科学的数据。对于精确制导火箭弹，毁伤过程是一个残缺信息的过程，是一个灰过程。但从作战角度出发，指挥控制本身就排除了火力毁伤中的灰过程。智勇雷、斗计华对舰空毁伤目标所需弹耗量计算建模中按照矩形毁伤率和椭圆毁伤率的方法进行计算［8］，得出的结果也较前述研究更为贴近实际。但远程制导火箭采用“卫星+惯导”组合导航后，其射击效率与评定方法也较以往有了许多变化。本文针对触发式卫星制导远程火箭技术特点，研究对单目标射击的射击效率问题。

1 远程制导火箭弹射击误差分析

1.1 误差源分析

射击效率是指对目标射击时所达到预定目标的程度［1］。从远程制导火箭武器的作战运用特点来看，其射击效率不但与武器系统本身有关，还与所打击的目标、射击目的和射击方法等因素有关。对于采用“卫星+惯导”组合导航模式的远程制导火箭，影响其射击精度的因素主要为：目标测量误差、发射点定位误差（惯导误差）、瞄准误差、制导工具误差、制导方法误差、火箭工艺非标准误差、气象因素、弹道随机干扰因素等。根据误差对落点散布的影响属性，可将其归为系统误差和随机误差。结合现有装备特点，子母弹等开仓式弹药误差还要考虑其开仓高度和子弹制导和非制导下落过程，该过程非本文研究的“卫星+惯导”组合导航过程，因此，本文只研究触发式火箭弹。在研究其散布规律时，认为总的射击误差是单个因素所引起误差之和，因而可用正态分布律作为散布律。

1.2 基于相关性射击的两组误差型分析

制导火箭对某一个目标进行射击时，有可能采用单发弹进行射击，也有可能采用连射、齐射方式进行射击［10］。前者的射击可认为是一个独立事件，是一种较为简单的情况。而在后者的射击当中，对同一目标射击的相邻两发弹之间的时间间隔很小，由于所有制导火箭弹弹道参数在发射前均已确定，前一发火箭弹发射时产生的扰动和气流对后续发射火箭弹的散布都产生影响。虽然制导火箭弹可以在发射后利用卫星或惯导导航信息对弹道偏差进行修正，但弹道解算装订的参数是以初始位置与方向确定的，因此，则各发弹之间仍会产生射击相关性。将相关射击中的总随机误差分为个别误差和集体误差两组相互独立的误差。在这种情况下，每一发弹的落点坐标的误差可分为如下3 部分：系统误差、集体随机误差、本发制导火箭弹的个别随机误差［2］。其中，系统误差是非随机性的，集体误差对各发弹的影响都相同，某发制导火箭弹的个别随机误差既独立于集体误差，又独立于其他各发弹的个别随机误差。于是，第i 发弹的弹着点坐标可表示为：

式中，UJ和VJ为射击集体随机误差；UGi和VGi为第i 发制导火箭弹射击的个别随机误差；x¯i和y¯i为系统误差，也即弹着点散布中心坐标。

据方差加法定理，第i 发制导火箭弹射击的标准差（方差）为：

式中，σxi、σyi为第i 发弹射击的标准差（方差）；σxJ、σyJ为集体随机误差的标准差；σxGi、σyGi为第i 发弹个别随机误差的标准差。

假设集体随机误差与个别随机误差之间相互独立，则两发弹之间射击误差的协方差为：

相邻两发制导火箭弹射击的相关系数为：

设参加射击的火箭弹弹种相同，则各发弹的个别随机误差服从相同的分布规律，其标准差是相同的，此时，x 坐标方向和y 坐标方向的误差标准差为：

任意两次射击的相关系数为：

2 触发式卫星制导远程火箭弹对单个目标的射击效率

“卫星+惯导”组合制导远程火箭弹有触发式和开舱式两种弹药，开舱式弹药如制导子母弹，其射击效能需考虑子弹开舱过程和下落过程，符合二元正态分布［3］，由于其主要用于对面积目标的压制射击，因此，本文只研究触发式远程火箭弹。

试验和理论计算表明，触发式远程火箭弹需要命中目标才能对其产生毁伤效能，在研究其射击效率时需要考虑命中目标的概率和命中后目标被毁伤的条件概率。若考虑到毁伤累积和射击相关性，需要用到成组射击的联合分布律进行积分计算，较为复杂。这里先不考虑毁伤积累问题，仅考虑射击相关性。

2.1 命中毁伤律

远程制导火箭弹采用“卫星+ 惯导”组合制导方式增加其命中概率，在不考虑电磁干扰的情况下在同一地点，对同一目标，射击其制导参数基本相同，其落点仍符合正态分布规律，如图1 所示。因此，可以设多发远程制导火箭弹的落点呈等概率正态分布，则其概率密度函数f（x，y）为：

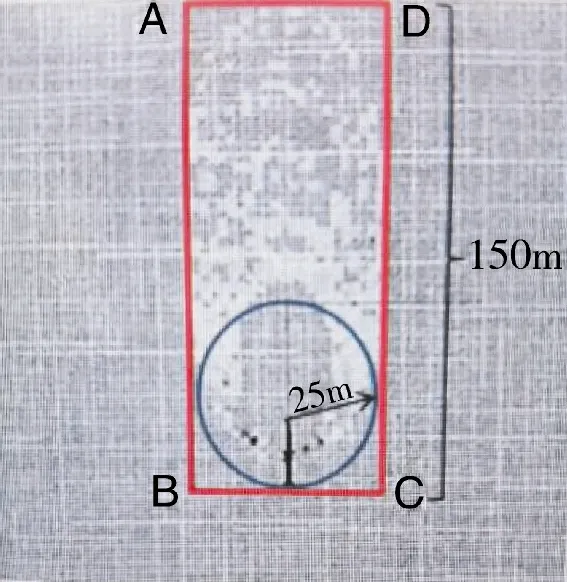
图1 触发式弹药动爆毁伤场Fig.1 Dynamic explosion damage field of trigger ammunition

其中，σx、σy分别是随机变量X 和Y 的标准差（方差）；ρ 是x 和y 方向的相关系数。

在不考虑强对抗环境对卫星导航信号干扰的影响状态下，其坐标轴与射弹主散布轴平行，则满足正态分布律的表达式为：

令m 为命中目标远程制导火箭弹的数量，G（m）为毁伤目标的毁伤律，研究其对坚固单个目标射击时，毁伤律与命中弹数有关。且因为m 的取值范围为非负整数，G（m）的取值为离散的点。用随机变量Ω 表示毁伤目标所需的必须命中弹数，则Ω的数学期望称为平均必须命中弹数，有：

取命中数为k∈N（N 为自然数集），可知命中目标的前（k-1）发火箭弹还没能达到毁伤要求，而命中第k 发后达到毁伤要求，也即必须命中弹数Ω=k的概率，就是第k 发命中才毁伤目标的概率。于是，G（m）可看作前m 发命中弹毁伤目标的概率，它是前（m-1）发命中弹已达毁伤目标的概率与第m 发命中才毁伤目标的概率之和，则Ω=k 的概率为：

考虑到G（k）≤1，且自然数N 充分大时，可得G（N）=1 命中毁伤律与平均必须命中制导火箭弹数之间的关系式为：

若不考虑单一目标的毁伤积累，可将命中毁伤律简化为指数毁伤律。假设一发命中弹毁伤目标的概率为Pdh，则m 发命中毁伤目标的指数毁伤律为

2.2 射击效率计算

假定n 发远程制导火箭弹中有m 发命中目标的概率为Pm，n，对目标的命中毁伤律为G（m），则n发制导火箭弹的射击效率为［3］

假设无损伤积累的射击相关性服从两组误差型，给定集体误差（x，y），毁伤目标的条件概率为：

再根据全概率公式积分求射击效率：

式中，fJ（x，y）为集体误差的概率密度函数，可以根据目标特性、弹药威力集体误差的大小加以确定。若目标毁伤律为指数毁伤律，则毁伤目标的条件概率可简化为：

式中，Pi（x，y）为在集体误差条件下第i 发远程制导火箭弹命中目标的条件概率，Pdhi为第i 发命中远程制导火箭弹毁伤目标的概率。在进行数值计算时，对于Pm，n（x，y）和Pi（x，y），可认为系统误差为（x，y），或将散布中心平移至（x，y）处。

2.3 射击效率计算的简化

对式（15）进行二维积分可求取对目标的射击效率，但因涉及到射弹散布律问题而较为繁琐。远程制导火箭弹是有卫星+ 惯导导航的可调控弹道弹药，综合上述散布影响因素，可以将单个目标看作以目标为中心的，由很多等概率网格组成的空间结构，取各弹独立射击时目标被毁概率为Wd，Wx为相关射击时目标被毁概率，相关系数为ρ，χ 为系数，则有

式中，Pdm为单发命中概率，Pdh为单发命中的毁伤概率，n 是发射的总弹数。

3 算例分析

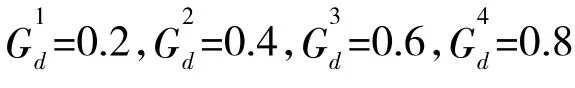
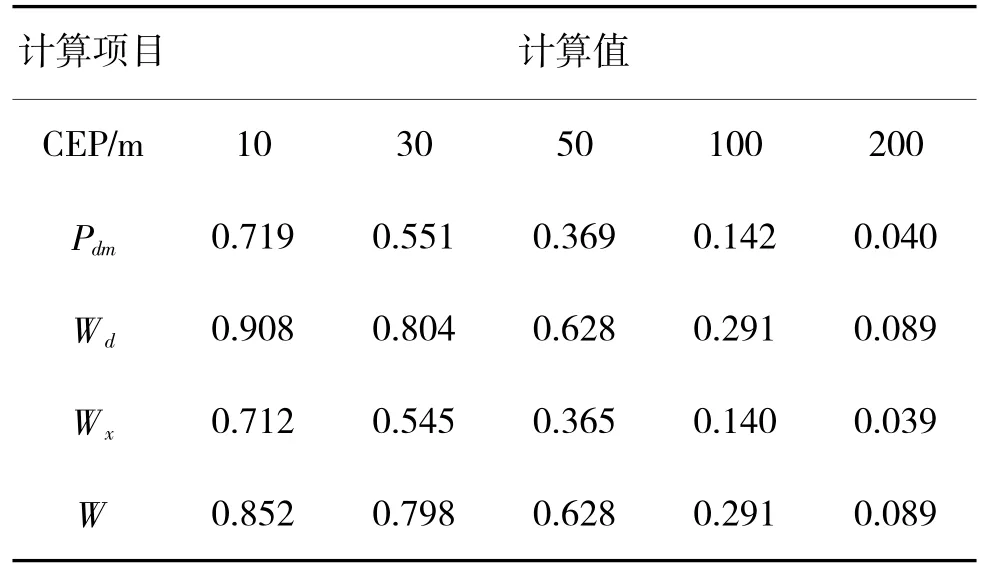
表1 用弹量为4 发的计算结果Table 1 The calculation results with the consumption of 4 rockets

表2 用弹量为3 发的计算结果Table 2 The calculation results with the consumption of 3 rockets

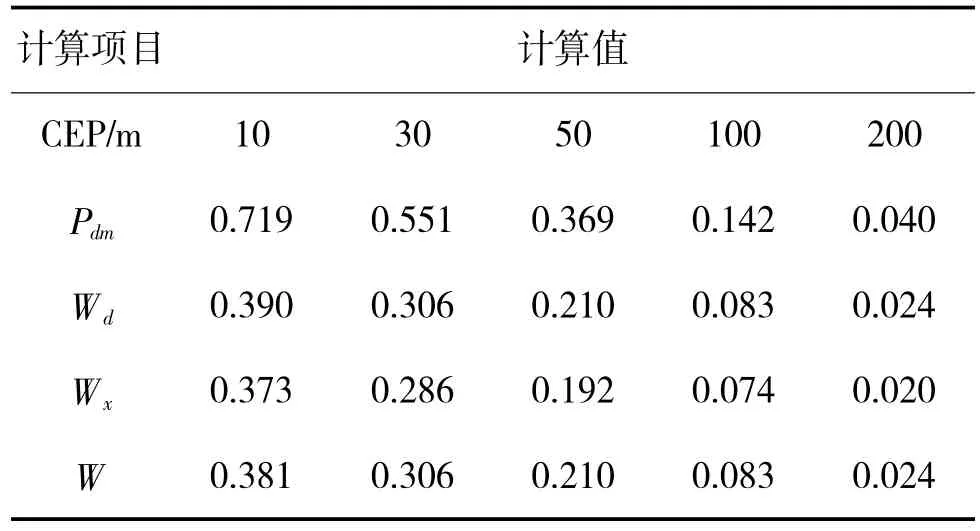
表3 用弹量为2 发的计算结果Table 3 The calculation results with the consumption of 2 rockets

由表1～表3 中数据可得，单发制导火箭弹命中概率以及不同用弹量时独立射击毁伤率、相关射击毁伤率、射击效率随CEP 的变化曲线，如图2～图5 所示。

图2 Pdm 随CEP 的变化曲线Fig.2 The variation curve of Pdm with cep

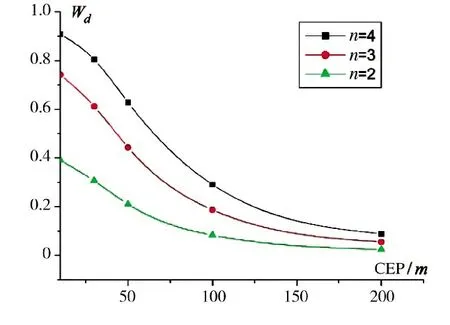
图3 不同用弹量Wd 随CEP 的变化曲线Fig.3 The variation curve of different number of consumption of rockets Wd with cep

图4 不同用弹量Wx随CEP的变化曲线Fig.4 Thevariationcurveofdifferentnumber of consumptionofrocketsWxwithcep

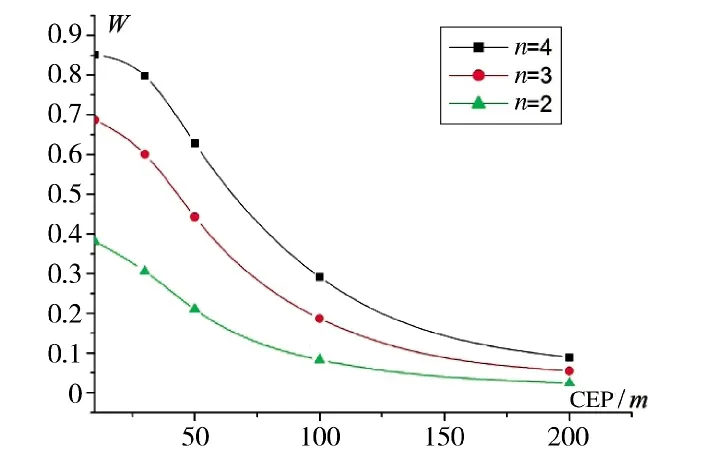
图5 不同用弹量W 随CEP 的变化曲线Fig.5 The variation curve of different number of consumption of rockets W with cep

由图2～图5 可知，单发命中概率、独立射击毁伤概率、相关射击毁伤概率和射击效率的值均随着CEP 的增加而减小。这是因为CEP 值越大，射弹散布越大，从而使命中概率和毁伤概率减小。在CEP值相同时，毁伤概率和射击效率随着用弹量的增加而增加。

由图5 可以看出，在CEP 相同时，射击效率W的值随着用弹量的增加而增加，且用弹量越多，W的值越趋近于1，这与毁伤律的物理本质也是相符的。还可以看出，随着CEP 的增大，射击效率刚开始急剧减小，在CEP 增大到100 m 左右后趋于平缓，且保持在一个较低的毁伤程度。要造成这样大的散布，一般是由于卫星导航失去作用而仅靠纯惯导工作，这也说明了保持卫星导航设备正常工作是确保高射击效率的重要工作。

在图5 的算例中，当CEP 值为10 m 时，在考虑了目标测量误差的条件下，采用2 发远程制导火箭弹对该目标的射击效率即可达到近40%（中度毁伤），用4 发弹的射击效率即可高达85%（毁歼）。而在实际射击过程中，若目标测量误差很小、制导正常，CEP 值可达米级，则射击效率更高。

由图6 可以看出，在用弹量分别为4 发、3 发、2发时，每发弹独立射击毁伤概率在开始时先是大于射击效率的值，随着CEP 的增大，独立射击毁伤概率与射击效率的值逐渐逼近。这是因为随着散布越大，各发弹之间的射击相关性越小，就越趋近独立射击的状态。

图6 不同用弹量W 与Wd 对比曲线Fig.6 The comparison curve of different number of consumption of rockets W with Wd

同时，由表1～表3 可以看出，对于该目标射击时，CEP 不大于30 m 时1 发弹命中即可对目标达到中度毁伤要求。当然，实际射击中对目标的射击效率与用弹量、目标性质和火箭精度密切相关，需具体讨论。

4 结论

采用两组误差型分析了触发式卫星制导远程火箭弹的误差因素，推导了对单个目标射击的命中毁伤律和射击效率公式，在不同用弹量和不同CEP情况下的计算结果表明：远程制导火箭弹射击效率与打击目标性质、制导精度和命中弹数密切相关。对同一目标，射击效率随制导精度CEP 增加而减小，随用弹量增加而增加。制导精度CEP 值越大，射击独立性越强。