深孔麻花钻静刚度半经验模型研究
曾滔,刘战强,左小陈,汤爱民
1山东大学机械工程学院;2株洲钻石切削刀具股份有限公司
1 引言
静刚度对刀具切削性能的影响很大,其反映了刀具在静载荷下抵抗变形的能力,可用其几何结构的变形量来衡量静刚度的大小,刀具静刚度越大,其受力时产生的变形越小。刀具刚度不足会导致加工中产生振动,引起加工表面振纹和加工精度超差等问题,严重时甚至导致刀具折断。相对于普通钻头,深孔麻花钻长径比大,刚性相对较差,为保证其切削性能,静刚度是设计结构的重要考虑因素之一。
麻花钻静刚度的研究主要包括定性分析和定量计算两方面。定性分析常采用有限元软件分析钻头关键结构参数如芯径、螺旋角、槽长、排屑槽面积、排屑槽参数对刀具刚度的影响,优化麻花钻结构设计参数。谢大纲等[1]通过有限元分析证明了增大芯厚能提高麻花钻刚性,但芯厚过大会导致负面影响,需要合理修磨横刃。宁明志等[2]针对不同截面形状的麻花钻进行变形和模态分析,得出钻头横截面轮廓线的内切圆直径与钻芯直径比为1~1.5时钻头综合性能最优的结论。言兰等[3]利用ANSYS对比分析了微钻结构参数变化对钻头刚度的影响,结果表明微钻头芯径与直径之比取0.3~0.4甚至更大时刚度较好。刘小川等[4]研究表明,微钻头芯径与直径之比取0.18~0.28刚性较好,与前者的研究结论略有不同。许立福等[5]研究表明,同等芯厚时,直槽钻头比螺旋槽钻头抗扭刚性好,该结论与陈婧[6]的研究可以相互印证。靳交通等[7]对比两种不同截面形状的麻花钻受力时的扭转变形,验证了所设计的异形螺旋槽具有更好的钻体刚度,实现螺旋槽结构优化。
定量计算一般是通过简化麻花钻横截面几何模型,计算截面的惯性矩和惯性积,应用弹性力学理论或有限元法建立可间接计算麻花钻刚度的模型。 Huang B.W.等[8]采用带局部裂纹的预扭梁模拟带裂纹的钻头,建立了具有时变边界条件的钻头振动模型,并考虑裂纹、转速、预扭角和推力对钻头振动的影响,通过振动情况间接分析钻头刚性。R.H.Thornley等[9]通过研究钻尖不同结构参数与截面积、面积极矩特性之间的关系,提出了一种基于螺旋槽内切圆直径衡量麻花钻螺旋槽排屑能力的数学方法,建立了计算截面特性的经验方程。孙东明等[10]和万光珉等[11]应用弹性力学理论和有限元方法,通过计算对比不同截形的麻花钻扭转刚度,提出了高抗扭刚度麻花钻横截面优化设计方法,优化试制了一种新型麻花钻,并对钻头扭转刚度理论计算值和实测值进行对比,结果表明二者比较接近。Fang Chuan等[12]通过线性回归方法建立了以钻芯厚度、排屑槽面积和螺旋角为自变量的计算扭转刚度的经验公式。
根据麻花钻刚度的研究结论对麻花钻刚度进行定性分析时,可用芯径结合长径比间接表征弯曲刚度,用刀具径向截面内切圆直径与刀具直径的比值间接表征扭转刚度。需定量计算麻花钻刚度,根据麻花钻横截面轮廓的几何方程,应用圣维南原理求解复杂的应力函数[13]。
随着刀具技术的发展,麻花钻(特别是深孔麻花钻)的横截面形状越来越复杂,为了兼顾其刚性和排屑性能,通常将螺旋槽设计为成型槽,横截面轮廓为多段曲线光滑连接而成的自由曲线,建立求解其静刚度的理论模型难度较大。本文基于深孔麻花钻横截面几何性质计算模型,结合有限元仿真分析建立麻花钻静刚度半经验模型,预测深孔钻受力时的弯曲和扭转变形。
2 麻花钻横截面几何性质
理论上来说,麻花钻在使用过程中只受轴向力Fz和扭矩M作用,但由于实际切削过程中,径向力通常存在轻微不平衡,麻花钻受到径向力Fr作用,其受力模型可简化为图1所示悬臂梁结构。
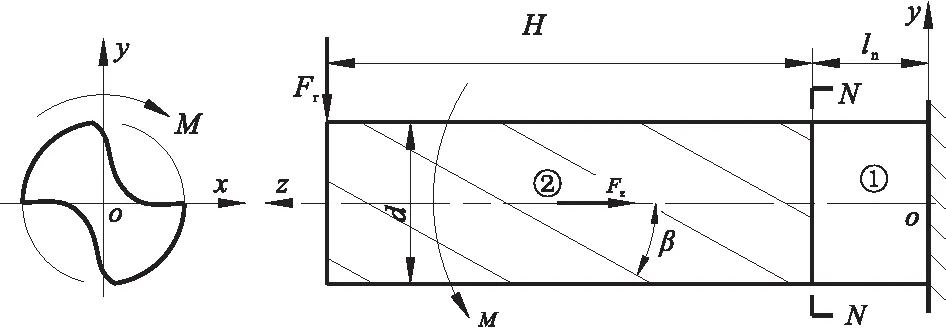
图1 麻花钻受力悬臂梁模型
图中,悬臂梁分成连接部分①和切削部分②,连接部分的长度为ln,d为切削部分直径,H为长度,β为螺旋角。麻花钻连接部分一般为圆锥或圆柱状,它对麻花钻刚性的影响程度由麻花钻刃部直径和柄部直径决定,变幅不大;而切削部分因麻花钻槽型设计的多样化,对麻花钻刚性的影响更复杂,故研究麻花钻的静刚度重点在于分析切削部分的静刚度。
如图2所示,粗实线表示麻花钻螺旋槽截面轮廓,虚实线表示麻花钻外径圆轮廓。假设麻花钻螺旋槽横截面轮廓曲线的解析方程为y=f1(x),外径圆轮廓曲线的解析方程为y=f2(x) ,则螺旋槽截面对坐标轴的惯性矩和惯性积为
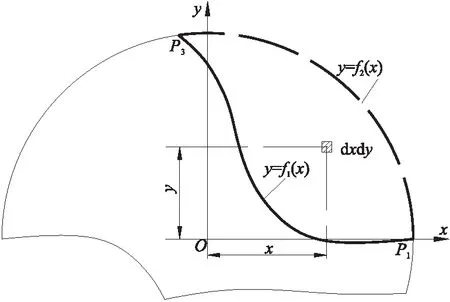
图2 螺旋槽截面性质积分求解
(1)
麻花钻有两条螺旋槽,且螺旋槽的横截面轮廓关于原点对称,如图1主视图所示。假设其中一条螺旋槽对坐标系o-xyz的x轴、y轴和原点o的惯性矩、惯性积分别为Ixf,Iyf和Ixyf,根据惯性矩和惯性积的转轴定理,可求得麻花钻横截面对坐标轴、坐标原点的惯性矩和惯性积为
(2)
麻花钻横截面对原点o的极惯性矩为
(3)
根据麻花钻螺旋槽的端截面轮廓方程和式(1)可计算出单个螺旋槽截面对x轴、y轴的惯性矩Ixf,Iyf和对原点o的惯性积Ixyf。再根据式(2)和式(3)可求出麻花钻横截面的几何性质。
3 深孔钻抗弯刚度模型
3.1 截面平均惯性矩
针对图1所示的悬臂梁结构模型,令ln=0,即只研究切削部分刚度,假设N-N横截面的实线轮廓如图3所示。横截面对x轴、y轴的惯性矩和惯性积分别为Ixt,Iyt和Ixyt。因麻花钻螺旋槽为螺旋状,不同位置处横截面相对于x轴的相位角不一样,其惯性矩也不相同。
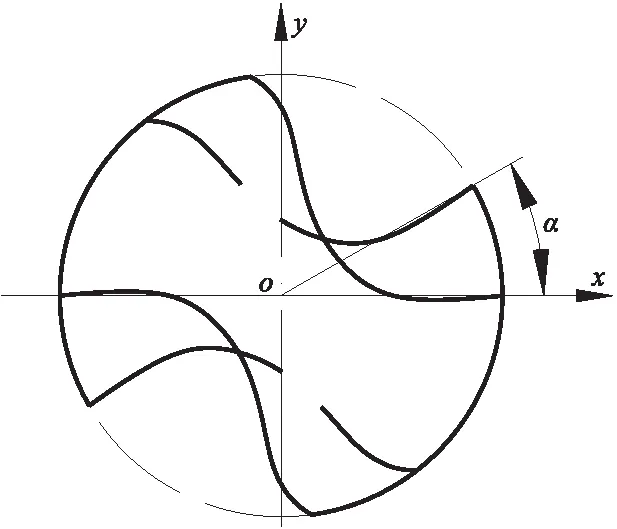
图3 切削部分横截面旋转
根据转轴定理,相对于N-N截面逆时针转动角度α的任意横截面(虚线轮廓)对x轴的惯性矩为
Ix2(z)=Ixtcos2α+Iytsin2α+Ixytsin2α
(4)
整理式(4)为
Ix2(z)=C1+C2sin(2α+σ)
(5)
有
(6)
麻花钻任意横截面对x轴的惯性矩Ix2(z)是以表征该截面距离端面的位置参数α为自变量,且与螺旋槽导程相关的周期函数,其最小周期为T=π。对深孔钻而言,切削部分长度大于螺旋槽导程,即H≥2πR/tanβ时,切削部分横截面对x轴的惯性矩存在极小值Ix2(z)min=C1-C2,极大值Ix2(z)max=C1+C2,如图4所示。
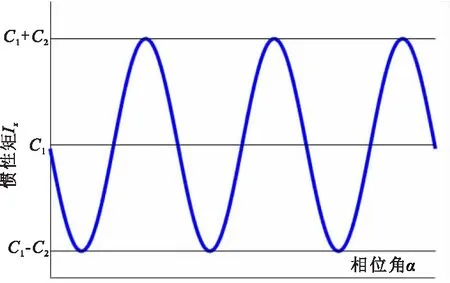
图4 横截面对x轴惯性矩的变化
虽然麻花钻切削部分任意位置处的横截面形状几乎一致,但由于螺旋槽的螺旋状特征,各横截面对x轴的惯性矩是以α为自变量的函数。为了简化结构模型,将麻花钻切削部分等效为等截面悬臂梁,并用所有截面惯性矩的平均值Iavg作为该悬臂梁的惯性矩。
惯性矩平均值Iavg为
(7)
式中,αH=2Htanβ/d。
根据式(7)绘制图5所示平均惯性矩—悬伸长变化曲线。图中直线表示极惯性矩Ip的一半(Ip=2C1),波浪线表示平均惯性矩Iavg,可见Iavg的大小随着刃长H的增大逐渐逼近极惯性矩的1/2,而且麻花钻越长,两者越接近。
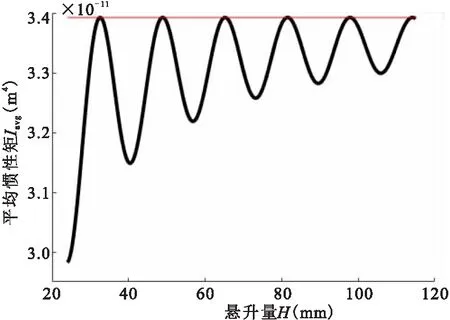
图5 平均惯性矩随刃长的变化
(d=6mm,β=30°,Ixt=3.272×10-11m4,Iyt=3.458×10-11m4,Ixyt= -1.904×10-11m4)
确定麻花钻螺旋槽横截面轮廓后,可根据其数学方程求得麻花钻截面惯性矩Ixt,Iyt和惯性积Ixyt,并将其代入式(7)中计算出横截面对x轴的平均惯性矩Iavg。
3.2 弯曲变形修正模型
对于长度为H且横截面为圆形的细长悬臂梁,若该梁只在自由端受到垂直于其轴线且向下的外力F时,根据材料力学,该梁在自由端的弯曲变形计算式为
(8)
式中,E为悬臂梁材料弹性模量;I为横截面对轴的惯性矩。
麻花钻的双螺旋槽结构使得其横截面为异形截面,减小了麻花钻的横截面抗弯系数,也导致在计算图1所示麻花钻悬臂梁自由端的弯曲变形时采用式(8)进行计算误差很大。由于麻花钻截面不规则,利用材料力学或弹性力学理论很难定量求解麻花钻悬臂梁自由端受径向力时的挠曲变形量,引入麻花钻弯曲变形修正系数Cb对式(8)进行修正。Cb越大,麻花钻抗弯刚度越小,受力时弯曲变形越大。
修正后的弯曲变形计算式为
(9)
根据式(9)可知,当麻花钻几何结构确定后,其抗弯刚度由弯曲变形修正系数Cb和截面平均值惯性矩Iavg两个因素决定。
3.3 弯曲变形仿真分析
针对直径6mm的深孔麻花钻,设计图6所示DHL,DHM和DHG三种不同的螺旋槽,建立深孔钻三维模型,开展静力学仿真,利用仿真结果拟合弯曲变形修正系数Cb,并实现参数辨识。
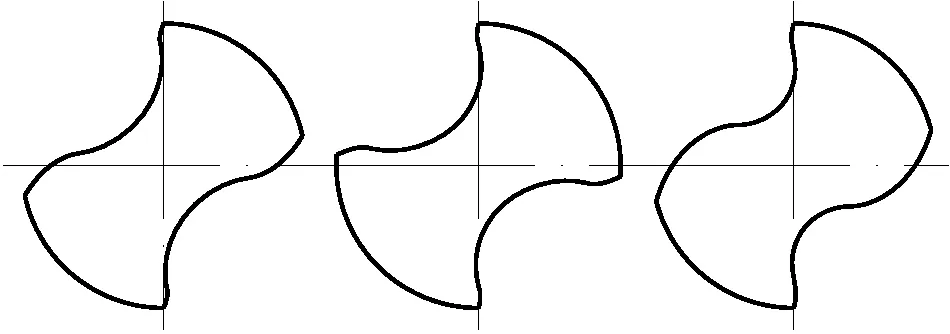
(a)DHL (b)DHM (c)DHG
图7为深孔钻三维模型,图中从上到下依次为1#,2#和3#深孔钻,分别对应DHL,DHM和DHG槽型。深孔麻花钻的钻芯设计有锥度,表1为钻芯的最大芯径、最小芯径、螺旋槽夹角(表征螺旋槽宽)、截面惯性矩和惯性积参数。麻花钻的材料类别、主要物理属性和网格控制方式设置见表2。
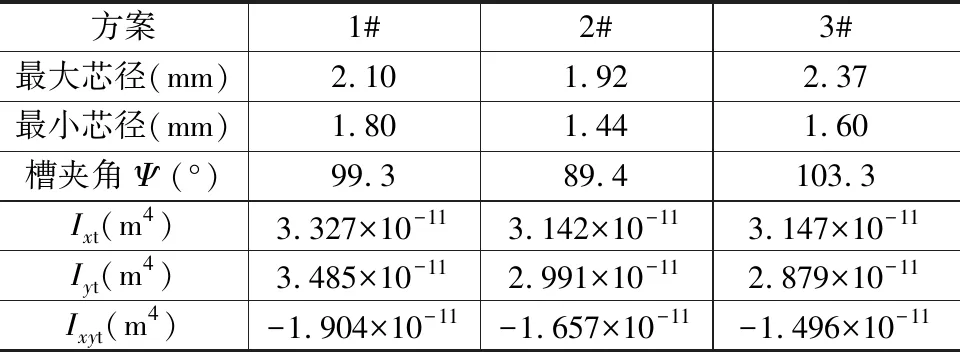
表1 直径6mm深孔麻花钻槽型特征值

表2 有限元分析参数设置

图7 深孔麻花钻三维模型
为保证与理论计算一致,仿真分析时忽略内冷孔对刚度的影响。图8为麻花钻的网格模型和加载条件,图中麻花钻靠近槽尾端固定,钻尖部分为自由端,在靠近钻尖处主刃带的微小范围内沿面法向加载均布压强,均布压强为10N径向力除以加载范围的面积。
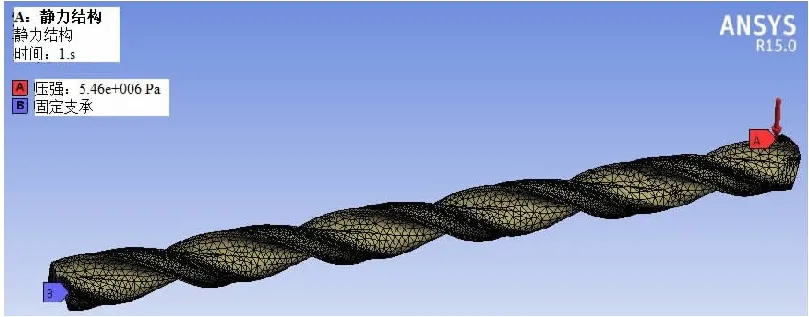
图8 弯曲仿真分析网格模型和加载方式
对于不同结构的麻花钻,因均布压强加载范围面积大小的差异,加载压强略有不同,1#,2#,3#深孔钻加载的均布压强分别为7.35MPa,5.34MPa和5.46MPa。分析悬伸H长度值分别为30mm,48mm,60mm,72mm,90mm五种情况时的每种深孔钻变形。经仿真计算,当悬伸H=90mm时,1#,2#,3#深孔钻的弯曲变形云图如图9所示。
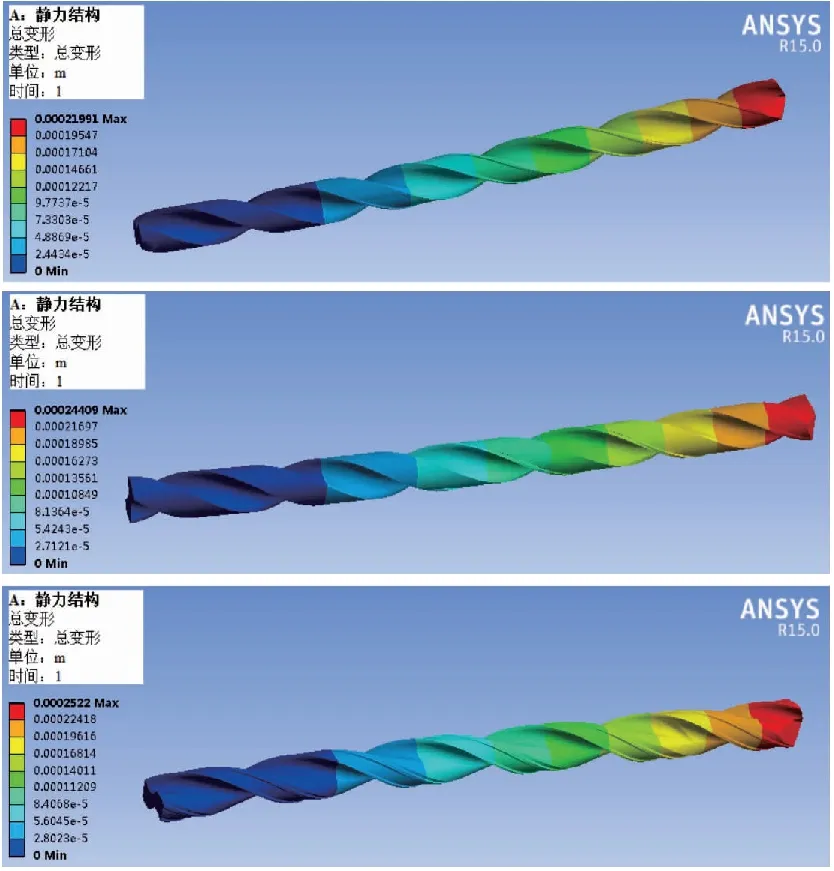
图9 弯曲变形云图(H=90mm)
根据图9和另外四种悬伸时深孔钻的弯曲变形云图获取不同悬伸长度时各深孔钻的弯曲变形仿真值,见表3。

表3 深孔钻弯曲变形仿真值 (mm)
3.4 修正系数辨识
由表1中的数据和式(7)计算出三种深孔钻不同悬伸长度时的横截面对x轴的平均惯性矩(见表4),可见平均惯性矩Iavg与C1值(极惯性矩的1/2)非常接近。
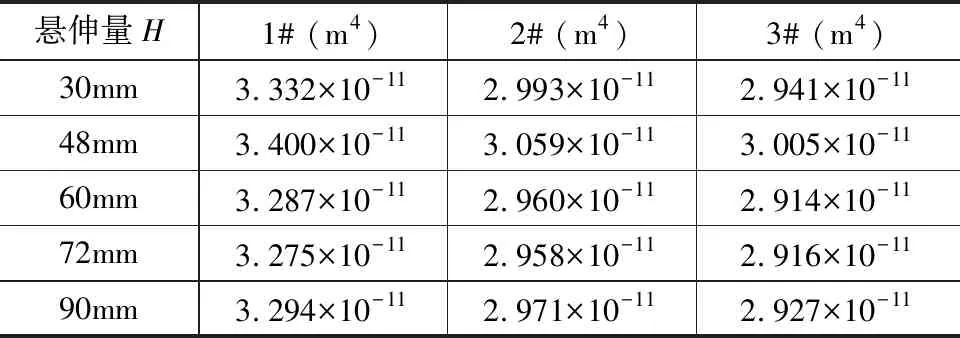
表4 深孔钻截面平均惯性矩Iavg
假设yi为弯曲变形观测值(仿真值),Yi为估计值(拟合值),由于不同悬伸长时弯曲变形差异达到数十倍,观测值与估计值之间的残差小时两者相对误差并不一定小,故采用相对误差平方和最小的方法对式(9)进行拟合,即求解合适的弯曲变形修正系数Cb,使得离散函数取得最小值为
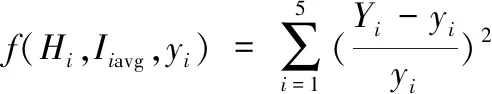
(10)
式(10)中要保证函数f(Hi,Iiavg,yi) 取得最小值,弯曲变形修正系数Cb需满足
(11)
通过计算得到1#,2#和3#深孔钻对应的截面弯曲变形修正系数的数值均在开区间 (1,2) 内,具体值见表5。

表5 深孔钻弯曲变形修正系数Cb
3.5 抗弯刚度模型
将表4中的平均截面惯性矩Iavg和表5中弯曲变形修正系数Cb代入式(9),求得不同深孔钻不同悬伸时的弯曲变形量估计值,将估计值与表3中的仿真值进行对比,分析两者之间的误差见表6。可见,最大拟合相对误差不超过7%。
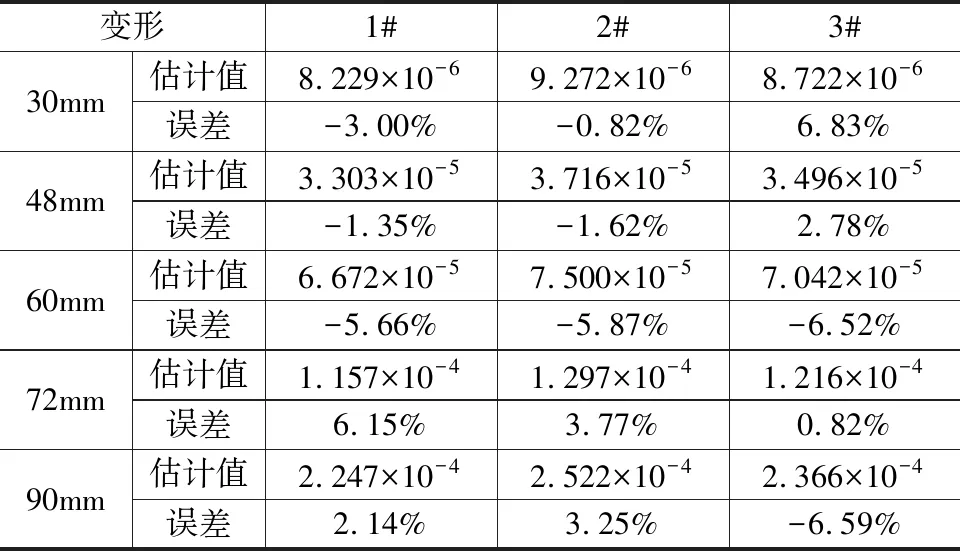
表6 深孔钻弯曲变形误差分析
为更直观地对比六种深孔钻弯曲变形的估计值与仿真值,根据式(7)、式(9)以及表6中的仿真结果绘制如图10所示变形拟合对比。图中三种曲线为深孔钻弯曲变形拟合曲线,其总体变化趋势与立方曲线吻合,但因为Iavg并非恒定常数,其值会随悬伸长度的变化而轻微变化,故拟合曲线在小范围内与立方曲线之间存在较小偏离;三种点数据为弯曲变形仿真值,点偏离拟合曲线的距离均很小,曲线拟合误差小。
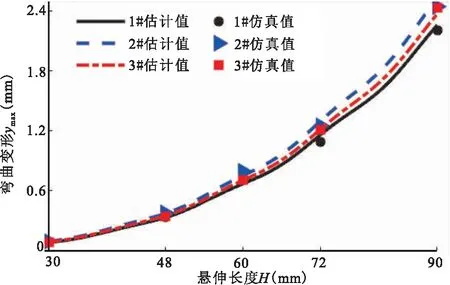
图10 弯曲变形拟合曲线
麻花钻抗弯刚度半经验模型为
(12)
4 深孔钻抗扭刚度模型
4.1 扭转变形修正模型
对于图1所示麻花钻悬臂梁模型,切削部分任意横截面的轮廓形状与N-N横截面相同,只是相对于N-N截面转动了角度α,由于极惯性矩不受转角影响,故当ln=0时,距离原点z且垂直于麻花钻轴线的任意横截面对截面中心的极惯性矩由式(3)计算得到。
对于长度为H,横截面为圆形的等截面细长杆,若圆杆只在自由端受到扭矩M,根据弹性力学理论可知,圆杆自由端截面相对于固定端的转角计算式为
(13)
式中,G为材料的剪切模量。
由于深孔钻横截面为非圆异形截面,不能直接应用式(13)计算麻花钻的相对扭转角,需引入引入麻花钻扭转变形修正系数Ct对式(13)进行修正。Ct越大,麻花钻抗扭刚度越小,自由端相对固定端的扭转角越大。
修正后的相对扭转角计算式为
(14)
根据式(14)可知,当确定深孔钻结构后,其抗扭刚度由扭转变形修正系数Ct和截面极惯性矩Ip两个因素决定,扭转变形与麻花钻悬伸长度成正比。
当深孔钻受扭时,其外圆周面的变形最大,由于深孔钻扭转角φ是微小量,对于半径为R的麻花钻,最大扭转变形与扭转角的关系为
(15)
4.2 扭转变形仿真分析
为求得深孔钻扭转变形修正系数,采用ANSYS软件对图7所示三种不同槽型结构深孔钻开展静力学仿真分析。材料类别、材料物理属性和网格划分和控制方式设置与弯曲变形仿真分析时相同。为保证仿真精度,钻体仅设计螺旋槽,忽略内冷孔、钻尖和刃背特征。
边界条件和加载方式设置如图11所示,麻花钻靠近槽尾端(左侧)固定,刃部为自由端(右侧),在距离刃部端面2mm范围内的刃瓣外圆周面上加载4N·m扭矩(载荷名为“Moment”)。针对每一种深孔钻,分析悬伸H长度值分别为30mm,45mm,60mm,75mm,90mm五种情况时的扭转变形。

图11 扭转仿真分析网格模型和加载方式(H=75mm)
经仿真计算,当悬伸H=75mm时,三种深孔钻的扭转变形云图如图12所示。可见,钻体上某个点处的扭转变形大小与该点到固定端的距离以及该点到轴线的距离都相关,距离越远,变形越大。
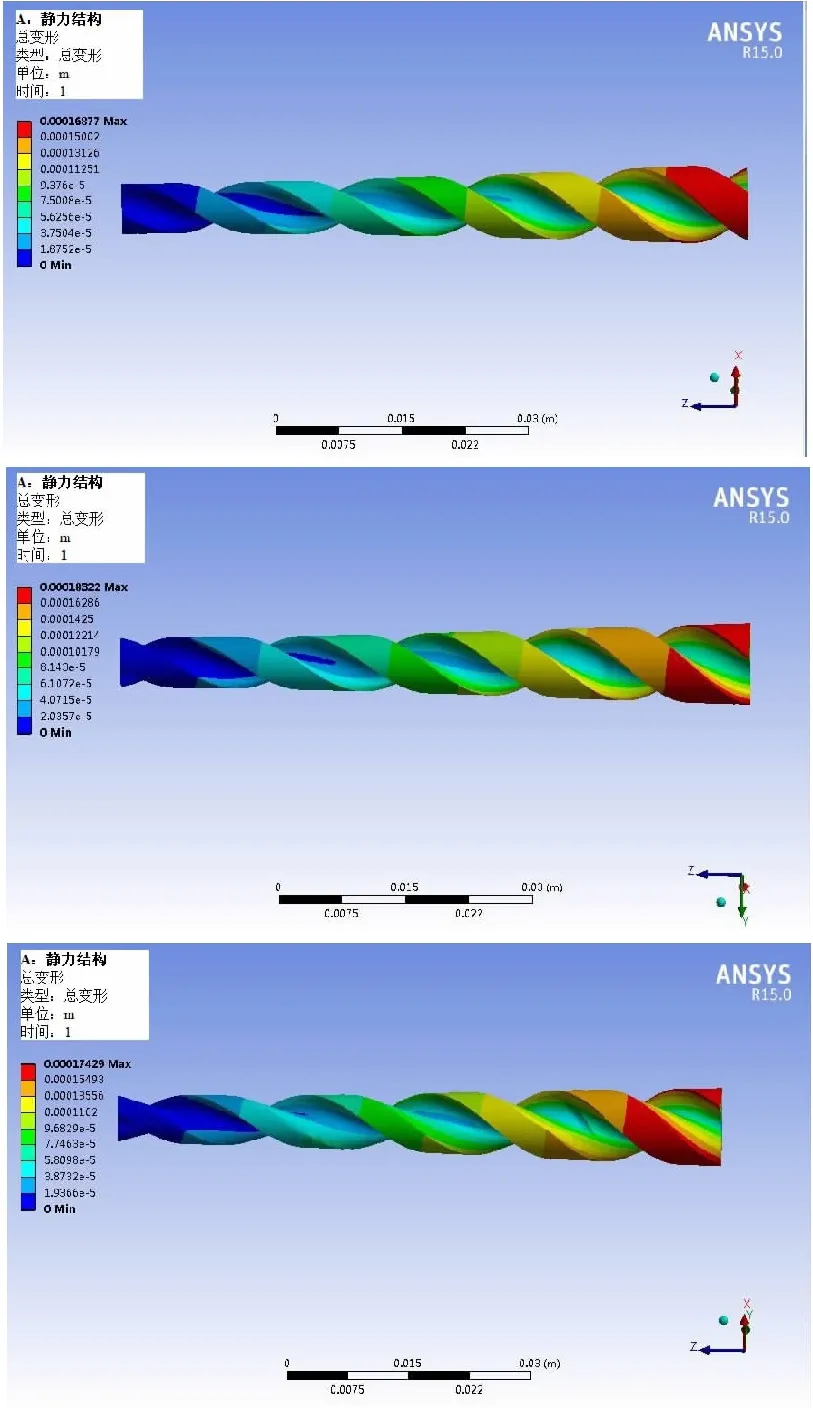
图12 扭转变形云图(H=75mm)
通过对直径10mm、不同长度的硬质合金圆柱棒模型加载同样的载荷进行仿真分析发现,其最大变形与通过式(15)计算得到的转角数值成正比,比值为5,说明扭转仿真得到的最大变形数据表示深孔钻外圆周面的最大扭转变形。
根据图12和另四种悬伸时深孔钻的扭转变形云图,获取各深孔钻不同悬伸长度时的扭转变形数值见表7。
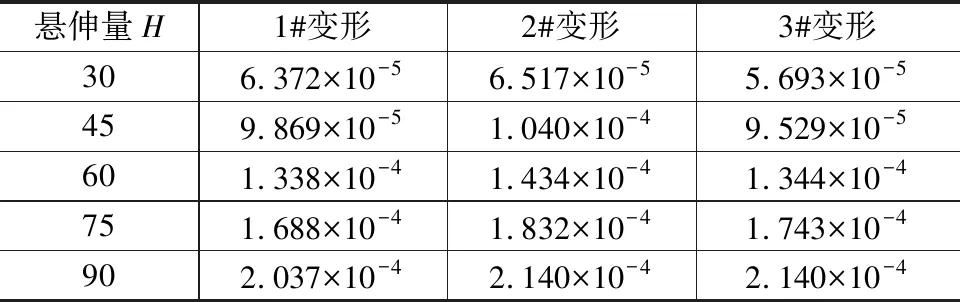
表7 深孔钻扭转变形 (mm)
4.3 修正系数辨识
假设yi为扭转变形观测值,Yi为估计值,同样采用相对误差平方和最小的方法对式(15)进行拟合。
求解合适的扭转变形修正系数Ct,使得离散函数取得最小值为
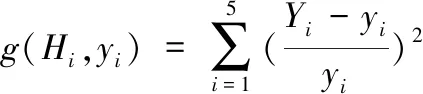
(16)
对于式(16),要保证函数g(Hi,yi)取得最小值,扭转变形修正系数Ct需满足
(17)
通过计算得到1#,2#和3#深孔钻对应的截面扭转变形修正系数,见表8。

表8 深孔钻扭转变形修正系数Ct
4.4 抗扭刚度模型
将表8中扭转变形修正系数Ct代入式(15),求得不同深孔钻不同悬伸时的扭转变形量,将估计值与表7中的仿真值进行对比,分析两者之间的误差见表9。
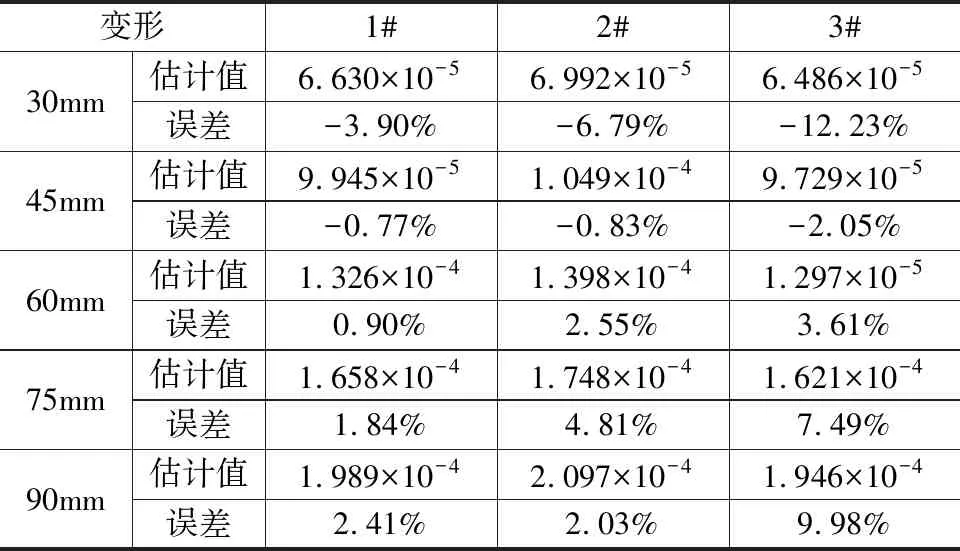
表9 深孔钻扭转变形误差分析
可见,3#深孔钻在悬伸长度H=30mm时拟合误差最大,为12.23%,其余情况下拟合的相对误差均在10%以内。为更直观地对比三种深孔钻扭转变形的估计值与仿真值,根据式(15)以及仿真结果数据绘制变形拟合对比见图13。图中,三条直线为深孔钻扭转变形拟合曲线,点数据为三种深孔钻的扭转变形仿真值。可见,1#和2#深孔钻五个点数据偏离曲线的距离较小,曲线拟合误差小,3#因个别点误差大,导致整体拟合误差偏大。
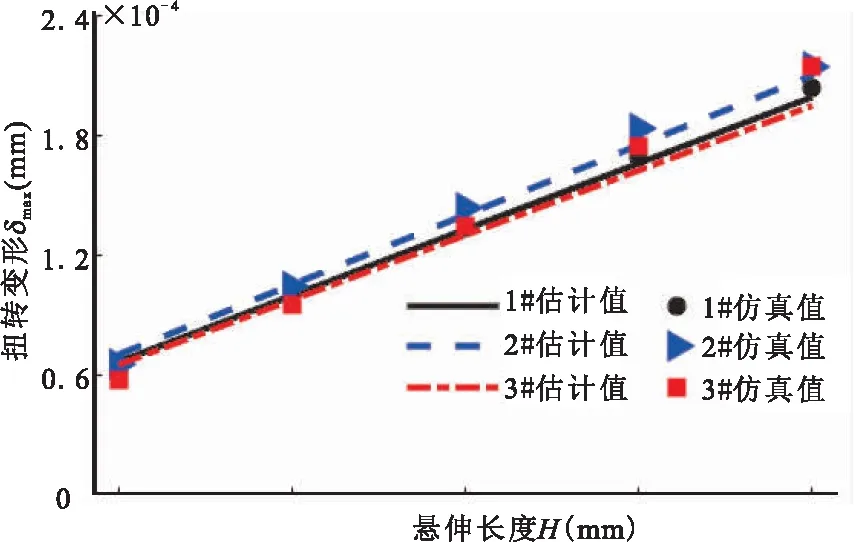
图13 扭转变形拟合曲线
可以确定深孔钻抗扭刚度半经验模型为
(18)
5 结语
(1)建立了麻花钻悬臂梁等效模型,推导了麻花钻截面惯性矩、惯性积、极惯性矩和截面平均惯性矩的数值计算公式。分析发现,随着刃长H的增大,麻花钻截面平均惯性矩逐渐逼近极惯性矩的1/2,而且麻花钻越长,两者越接近。
(2)提出了麻花钻弯曲和扭转变形修正系数,基于有限元分析和数值拟合的方法建立了麻花钻弯曲和扭转变形修正模型,并基于变形修正模型建立了深孔钻静刚度半经验模型。误差分析表明,修正模型预测麻花钻受力变形的精度小于13%。
(3)任意槽型结构的深孔钻受力时的弯曲和扭转变形均可类比圆截面杆受力时的变形进行计算,只需引入表征截面形状特性的变形修正系数对模型进行修正。结果表明,若进一步研究揭示刀具槽型结构与变形修正系数之间的对应关系,可实现刀具螺旋槽截形的优化设计,该结论也可应用于其他杆状切削刀具的受力变形计算模型中。

