输油管道运行能耗优化技术研究
王伟达
(大庆油田有限责任公司第六采油厂)
输油管道因其输量大、抗力强、安全性高等优点,被认为是最重要的油气输送方式。大型输油管道不仅在建设的前期投资巨大,且在服役期间的运行能耗也不容忽视[1-2]。随着油田的深入开发,油品物性、原油产量和工况参数等均发生变化,导致凭借现场经验制定的开泵方案和运行措施不再适用,造成运行能耗大幅上升,整体能耗费用逐年增长[3-5]。因此,有必要建立输油管道的运行能耗优化模型,在确保安全输送的前提下,制定经济合理的运行方案。
柳明富[6]通过动态规划法对输油管道开泵方案进行了求解,结果表明,可关闭两个中间泵站,直接越站实现全线输送;梁永图等[7]对输油管道不同时刻的离散问题进行单独求解,极大增加了求解速度;张天一等[8]对常规开泵方案、调转速方案和切割叶轮方案进行优选和对比,得到不同措施下的节能占比。以上研究对于输油系统能耗的优化具有重要参考价值,但均以开泵方案为优化目标,考虑到国内原油多为黏度高、凝点高、含蜡高的“三高”原油,在管输过程中需加热输送,而热能消耗通常占总能耗的80%以上,故需综合考虑热能和动能对运行能耗的影响。基于此,以总运行能耗费用最低为目标函数,在考虑水力、热力计算模型的基础上,通过约束函数限制开泵方案集合,并对总传热系数及水力摩阻系数进行校正,通过蚁群算法实现从开泵方案到运行参数的整体优化。
1 输油管道运行能耗优化模型
1.1 模型假设
由于管道水力、热力系统各变量间的非线性耦合情况较严重,故在建立模型时需进行部分假设,以简化求解过程。假设管道中的油品为单相均值不可压缩流体;管道采用密闭输送,短时间内输量和压力不发生改变;不考虑降阻剂、降凝剂的添加,即输送过程中原油物性不发生较大突变;不考虑径向温度的变化。
1.2 目标函数
同时考虑泵送原油消耗的电费和加热炉加热原油消耗的燃料费用,以总运行能耗费用最低为目标函数,见公式(1):
式中:S为总运行能耗,元/d;i为热站序号;n为热站个数;G为管输量,kg/s;ci为原油比热容,J/(kg·℃);TRi、TZi分别为第i个热站的出站温度和进站温度,℃;Ef为燃料油价格,元/t;ηfi为第i个热站的加热炉效率,%;BH为燃料的燃烧热值,取41 816 kJ/kg;j为泵站序号;m为泵站个数;Ep为电价,元/kWh;H为第j个泵站提供的扬程;ηpj为泵效率,%;ηj为电动机效率,%。
1.3 约束条件
热力约束需满足各热站的进站温度高于凝点以上3~5 ℃,出站温度不超过已有加热炉热负荷的最高出站温度,各站的流量满足质量守恒定量,具体见公式(2):
式中:Qi为第ηj个热站的流量,kg/s;Qi-min、Qi-max分别为满足热站热力负荷的允许最小流量和最大流量,kg/s;TZi-min、TRi-max分别为第i个热站的最低进站温度和最高出站温度,℃;
水力约束需满足进站压力约束、出站压力约束、全线水力约束等,保证各泵站提供的扬程大于沿程摩阻损失、局部摩阻损失和高程差的和,满足泵的吸入压力大于允许汽蚀余量,出站压头小于管道的最大承压范围,具体见公式(3):
式中:Gj为第j个泵站的流量,kg/s;Gj_min、Gj_max分别为满足泵站水力负荷的允许最小流量和最大流量,kg/s;Houtj、Hinj分别为第j个泵站的出站压头和进站压头,m;Hj为第j个泵站输油泵的扬程,m; Δhj为水力损失,m;Hp为管道全线所需压头,m;hj为沿程摩阻损失,m; ΔZ为高程差,m;hm为局部摩阻损失,m;Hj_min、Hj_max分别为满足泵站正常运行的允许最小压头和最大压头,m。
1.4 求解方法
对于运行能耗优化这类非线性问题,可采用动态规划算法求解。但对于热站、泵站数量多、运行调度周期长的长输管道而言,动态规划算法属于分层求解,不仅耗费更多的计算时间,且得到的解有可能是局部最优解[9-11]。因此,采用智能算法中的人工蚁群算法求解。
公式(1) 以运行费用最小值作为目标函数,为匹配人工蚁群算法特点,将其转化为最大值函数。将输油管道上的I个热站或泵站定义为N维空间,每个站内所能组合的开泵和开加热炉方案总数为Np,N维空间中的每一个位置表示管道对应的一种运行方案,将每种方案的数据代入目标函数,将求解结果作为食物信息素,从而实现不同蚂蚁位置信息的更新。具体步骤如下:
1) 初始化种群,确定蚂蚁数量、移动次数、食物浓度挥发常数及搜索限制。
2)根据蚂蚁移动的位置概率函数,确定蚂蚁的移动方向和速度,对于已经移动过的位置禁止再次移动。
3)所有蚂蚁完成一次移动后,更新信息素增量,检查是否满足终止条件,如不满足重新返回第2)步骤,如满足输出信息素浓度最高的位置作为最优解。
2 案例分析
2.1 基本情况
以某输油管道为例,该管道全长710 km,管径ϕ813 mm×14 mm,除首站、末站外,共有3 个热泵站,站内均有3 台外输泵和3 台加热炉,全线设计压力6.5 MPa,全年运行时间350 d。管道埋深1.5~2 m,管道导热系数为1.6 W/(m·℃),管道比热容0.5 kJ/(kg·℃)。管道沿线高程及站点分布见图1。
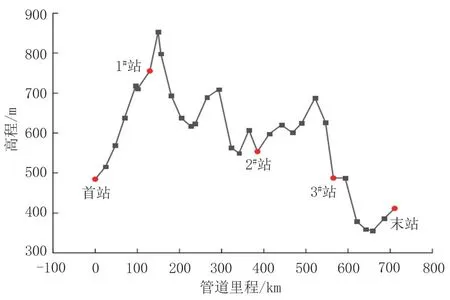
图1 管道沿线高程及站点分布Fig.1 Elevation and station distribution along the pipeline
2.2 热力模型修正
总传热系数K是影响站间原油温降的主要因素,其结果受管道导热系数、土壤导热系数、保温层导热系数、油品黏度、密度等因素的影响,正向求解需先假定一个管壁平均温度初始值,根据热平衡关系迭代得到计算总传热系数K′。但以上计算属于定义式,结果并不准确,在此利用探针法测试管道沿线的土壤导热系数,通过现有运行数据反算实际总传热系数K″,并利用最小二乘法建立K′和K″ 之间的关系,对K′进行修正。以首站至1#热泵站为例,首站至1#热泵站的热力分析见图2,总传热系数修正结果见图3。随着输量的增加、环境温度的升高、起点温度的降低,输油管道的运行状态越优,介质与管壁、管壁与土壤之间的换热越小,沿程温降越小,总传热系数越小。修正过后,热力模型的平均计算误差小于3%。
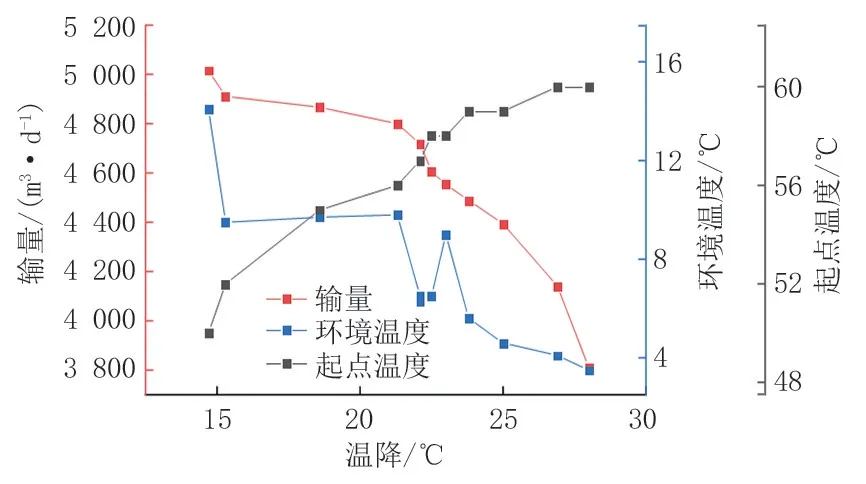
图2 首站至1#热泵站的热力分析Fig.2 Thermodynamic analysis from the first station to 1# heat pump station
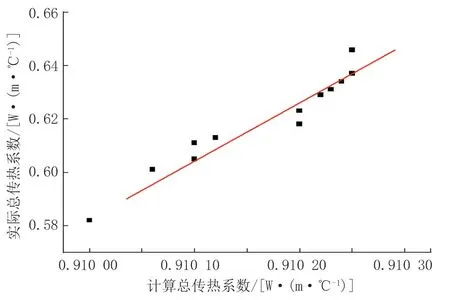
图3 总传热系数修正结果Fig.3 Correction results of total heat transfer coefficient
2.3 水力模型修正
由于管道自身退化和现场数据采集的误差等因素,按照传统公式计算的沿程摩阻损失hj与实际结果存在较大误差,这将直接影响站间压降的计算。根据达西定律,hj与管径、管长、流速及水力摩阻系数λ 等相关,其中管径和管长为固定值,流速与输量及生产运行任务相关,水力摩阻系数与雷诺数和管壁当量粗糙度有关,对水力摩阻系数进行修正可直接提高输油管道水力计算的精度。同理,参照热力模型修正方法,通过现有运行数据反算实际水力摩阻系数λ″ ,并利用最小二乘法建立计算水力摩阻系数λ′和λ″之间的关系,对λ′进行修正。以首站至1#热泵站为例,首站至1#热泵站的水力分析见图4,水力摩阻系数修正结果见图5。随着输量的降低、起点压力的降低,输油管道的运行状态越优,介质流速越慢,沿程压降越小,总传热系数越小。修正过后,水力模型的平均计算误差小于5%。
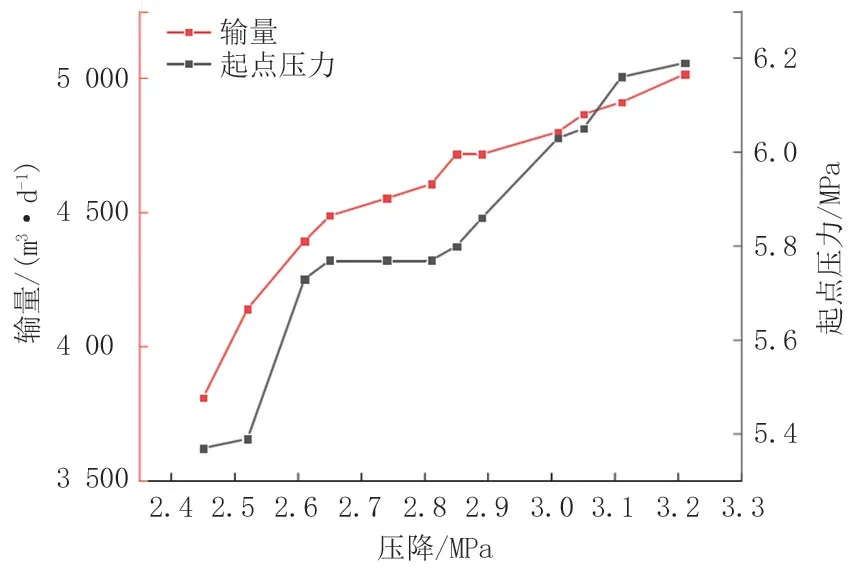
图4 首站至1#热泵站的水力分析Fig.4 Hydraulic analysis from the first station to 1# heat pump station

图5 水力摩阻系数修正结果Fig.5 Correction results of hydraulic friction coefficient
2.4 优化结果分析
设置蚂蚁数量为300、移动次数为100、食物浓度挥发常数0.5,优化前后的管道的温度变化情况见图6。不同管段优化后的温度均低于日常运行油温,其中首站至1#站的温降幅度最大,平均为11.5 ℃;3#至末号站的温降幅度最小,平均为7.1 ℃;全线平均温降为9.6 ℃,温降损失从14.7 ℃降低至9.6 ℃,各热站的出口温度有所降低,说明加热炉负荷有所减小,达到了节能降耗的目的。
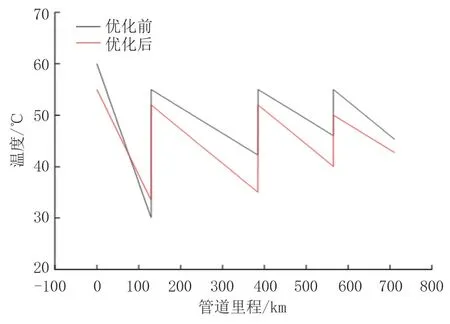
图6 管道沿线温度优化结果Fig.6 Temperature optimization results along the pipeline
优化前后管道的压力变化情况见图7。不同管段优化后的压力均低于日常运行压力,387 km 处的压力最大为5.06 MPa,末站处的压力最小为1.35 MPa,说明优化后管道全线的压能得到有效利用,输油泵负荷有所减小,达到了节能降耗的目的。
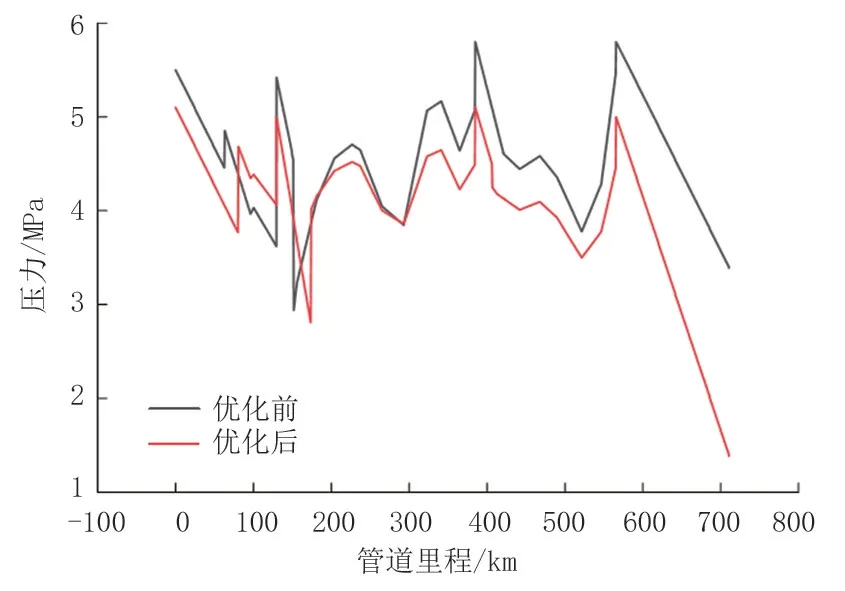
图7 管道沿线压力优化结果Fig.7 Pressure optimization results along the pipeline
综合优化后的水力、热力参数和设备的能效情况,核实每个站开泵和开加热炉的运行方案,输油管道优化前后的运行方案对比见表1。优化后,全线加热炉开启数量减少3 台,输油泵开启数量减少2 台,每日合计节约运行能耗费用0.53 万元。
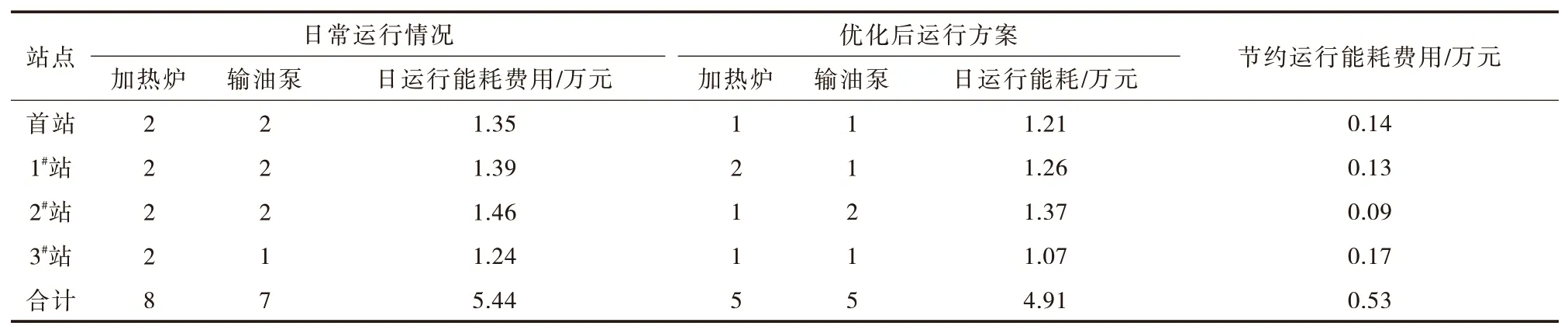
表1 输油管道优化前后的运行方案对比Tab.1 Comparison of operation schemes before and after optimization of oil pipelines
3 结论
1)针对目前输油管道运行能耗较高,站内泵机组和加热炉与输量变化不匹配的现象,以总运行能耗费用最低为目标函数,在考虑热力约束和水力约束的条件下,采用人工蚁群算法对开泵和开加热炉方案进行了优化,优化后各热站的出口温度有所降低,全线的压能得到有效利用,说明算法科学有效,达到了节能降耗的目的。
2)为提高管道沿线温降和压降计算结果的准确性,对总传热系数和水力摩阻系数进行线性修正,修正后热力模型和水力模型的计算误差分别小于3%、5%,可满足后续优化求解的要求。

