基于双超混沌映射的伪随机序列发生器设计＊

张 爽，李 震

(1.贵阳人文科技学院大数据与信息工程学院，贵州 贵阳 550025；2.贵州大学大数据与信息工程学院)

0 引言

伪随机序列是由确定性算法生成的随机数序列，它具有均匀统计特性[1]。混沌系统作为一种伪随机序列生成源[2]，与线性同余法和单向函数等其他生成源相比，其更容易实现，且具有长期不可预测的优点[3-5]。近年来，基于混沌的伪随机序列发生器设计研究[6-10]如火如荼。现有的伪随机序列发生器研究大致分两类：一类研究是基于低维混沌映射生成伪随机序列，如Logistic、Henon 和Tent 等混沌映射。该方法运算简单，混沌轨迹易预测，但这必然存在攻击威胁[11-12]。另一类研究是基于高维混沌系统生成伪随机序列，如Lorenz 和Chen 等混沌系统。这些方法在运行中都存在一个不可避免的问题，就是混沌退化问题[13]。混沌退化是由于数字设备的计算和存储精度受限而导致混沌系统出现短周期甚至性能退化。有关的研究如文献[14]提出一种基于时空混沌的伪随机序列发生器算法[15-16]。该算法把混沌系统中的浮点型数据直接转换成了整数型数据。这种让数字精度下降的方式必然引发混沌退化问题。王永等人[17]利用有限精度下暂态数据均匀性特点设计了一种基于整数Logistic 映射的伪随机数生成算法，可以有效保障输出序列概率密度分布均匀。文献[18]中阐述了由于混沌退化导致加解密成功率降低的问题。

计算机有限精度下的混沌退化问题是目前影响伪随机序列发生器性能的重要因素，基于此，本文提出一种基于双超混沌系统耦合的伪随机发生器算法，以解决有限精度下混沌退化导致的伪随机序列发生器的性能问题。本文从研究背景和研究现状出发，给出伪随机序列发生器的具体方案，并在此基础上提出一种音频加密方案。我们采用NIST（National Institute of Standards and Technology）的SP800-22 Revision 1a 标准对所提出的伪随机序列发生器方案进行随机性检测，并对音频加密方案仿真分析。

1 超混沌系统

1.1 超混沌2D-SLIM系统

超混沌2D-SLIM（Two Dimensional Sine Improved Logistic Iterative Chaotic Map）系统[20]是二维离散系统，其差分方程表示如下：

其中，a、b 为超混沌系统的控制参数。当控制参数设置为，初值x0=-0.3、y0=0.5 时，超混沌2D-SLIM系统相图如图1所示。

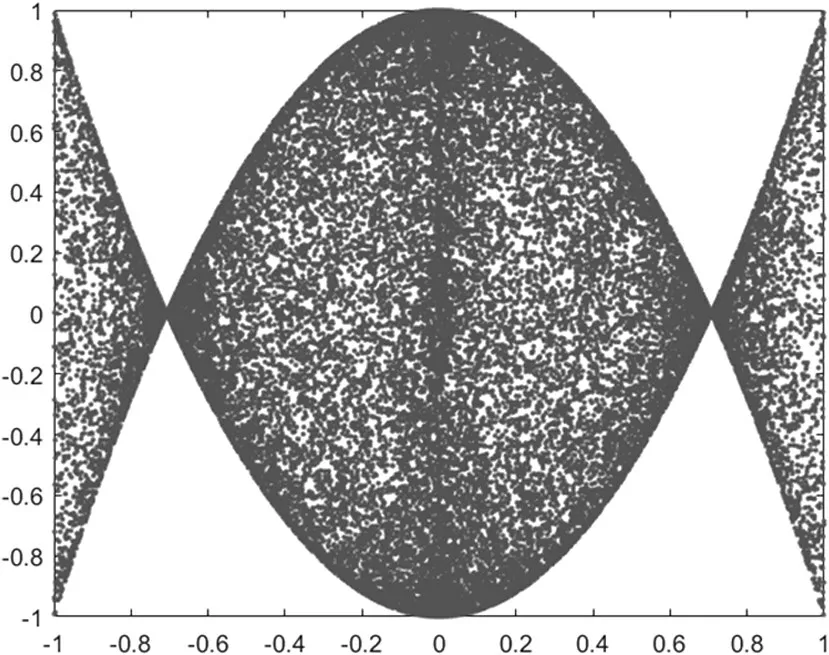
图1 超混沌2D-SLIM系统相图

当aϵ(0,3)且b=2π 时，超混沌2D-SLIM 系统的Lyapunov 谱如图2 所示。当a=1 且bϵ[4,7]时，超混沌2D-SLIM系统的Lyapunov谱如图3所示。

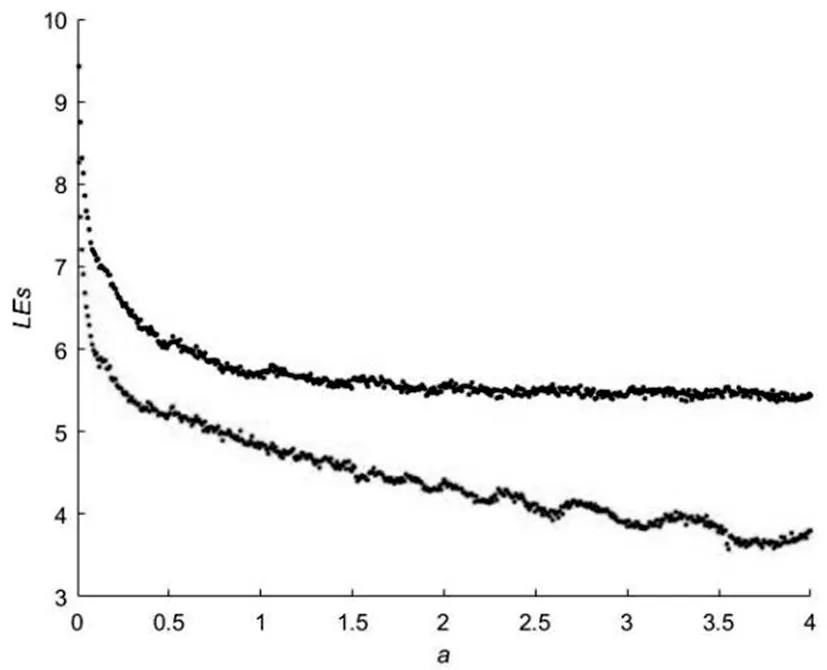
图2 超混沌2D-SLIM系统的Lyapunov谱(b=2π)

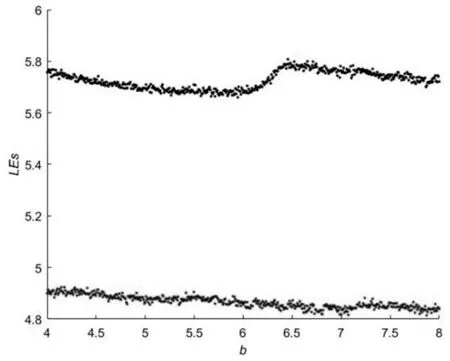
图3 超混沌2D-SLIM系统的Lyapunov谱(a=1)

由图2和图3可知，当a=1且bϵ[4,7]时，或aϵ(0,3]且b=2π时，系统处于超混沌状态。

1.2 超混沌2D-LSCM系统

超混沌2D-LSCM（Two Dimensional Logistic Sine Coupling Map）系统[21]是二维离散系统，其差分方程表示如下：

其中，θ 为控制参数。当控制参数设置为θ=0.99，初值x0=0.8、y0=0.5 时，超混沌2D-LSCM 系统相图如图4所示。

图4 超混沌2D-LSCM系统相图

当θ ∈(0,1)θϵ(0,1)时，超混沌2D-LSCM 系统的Lyapunov谱如图5所示。

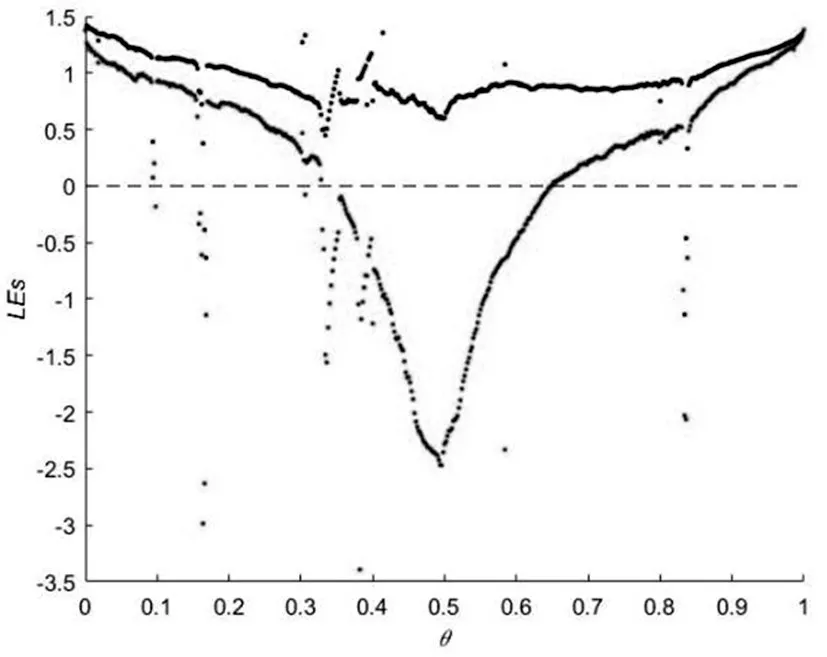
图5 超混沌2D-LSCM系统的Lyapunov谱

由图5可知，当θ ∈(0,1)时，超混沌2D-LSCM系统处于混沌状态。当θϵ(0,0.096)∪(0.1,0.156)∪(0.17,0.304)∪(0.308,0.328)∪(0.65,0.83)∪(0.84,1)时，超混沌2D-LSCM 系统具有超混沌行为，同时表明超混沌2D-LSCM系统具有复杂的动力学行为。

2 伪随机序列发生器设计及音频加密方案

本章基于超混沌2D-SLIM 系统和超混沌2DLSCM 系统提出一种双超混沌映射耦合的伪随机序列发生器，并在此基础上设计一种音频数据加密方案。

2.1 伪随机序列发生器整体结构

双超混沌映射耦合的伪随机序列发生器整体框图如图6所示，具体流程如下：

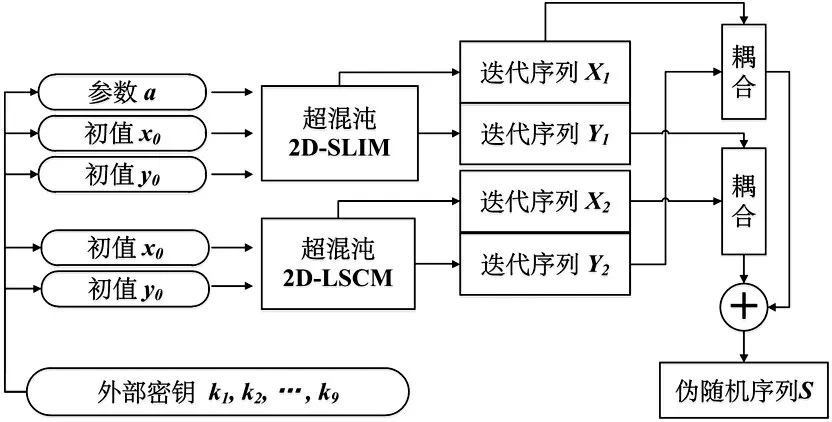
图6 伪随机序列发生器的整体结构图

⑴输入外部密钥k1,k2,….k9∈(0,1)。

⑵生成超混沌2D-SLIM系统的初值和参数。

⑶生成超混沌2D-LSCM系统的初值和参数。

⑷ 迭代超混沌2D-SLIM 系统和超混沌2DLSCM 系统，并根据公式（10）加入周期性扰动，将超混沌2D-SLIM 系统的迭代序列记为X1、Y1，将超混沌2D-LSCM系统的迭代序列记为X2、Y2。

其中，mod(a,1)表示a的小数部分。

⑸采用公式⑾将X1、Y2映射为二值序列X，根据公式⑿将X2、Y1映射为二值序列Y，由公式⒀生成伪随机序列S。

2.2 音频数据加密方案

基于2.1 节提出的伪随机序列发生器，设计一种音频数据加密方案，该方案的整体框图如图7 所示。具体流程：首先对音频数据进行采样处理。采样是指将音频数据从模拟信号转化成数字信号；其次采用公式⒁对数字信号进行量化处理[22]。

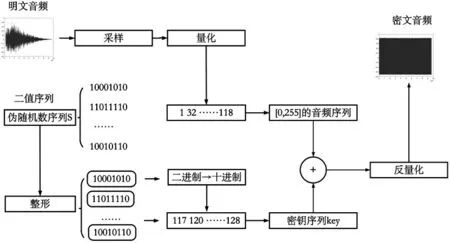
图7 音频数据加密方案

其中，A 表示音频数据的数字信号，Max 和Min 分别表示音频数据数字信号中的最大值和最小值。该步骤可将音频信号量化至[0,255]的范围内，将量化后的序列记为S1。随后对生成的二值伪随机序列S 进行整形处理和进制转换处理，处理后将获得一串序列，将此序列记为加密密钥key。其中整形处理是将S 分为多个长度为8 比特的序列段。进制转换处理是将8 比特的序列段转换成十进制整数。最后将序列S1与密钥key进行异或处理生成加密后的数字音频信号S2，再通过公式⒂进行反量化[22]输出加密后的音频信号S3。

式⒂中，Max 和Min 为明文音频数据数字信号中最大值和最小值。解密方案的整体框图如图8 所示，具体步骤：首先将密文信号按式⒁进行量化处理；然后将量化后的整数序列与密钥key 进行异或处理；最后将处理后获取的整数序列按式⒂进行反量化处理。处理后即可获取明文。

图8 音频数据解密方案

3 实验仿真

本节首先采用NIST的SP800-22 Revision 1a标准对本文提出的伪随机序列发生器进行性能分析，随后对本文提出的音频加密方案进行仿真验证。本节仿真硬件环境为Intel(R) Core(TM) i9-10885H CPU @2.40GHz 2.40GHz和128G内存，软件环境为Windows 10家庭中文版和MATLAB R2016a。外部输入密钥为：

k1=0.359484151546519、k2=0.151564685164879、

k3=0.123154888888914、k4=0.894654315461566、

k5=0.648456415484648、k6=0.548481689647833、

k7=0.489465425189611、k8=0.735465156869472、

k9=0.689452654115786

3.1 随机特性检测

采用NIST 的SP800-22 Revision 1a 标准对本文提出的伪随机序列发生器进行性能分析，如果测试结果P-value 值≥0.01，表明伪随机序列具有良好的随机特性。表1为SP800-22 Revision 1a的测试结果。

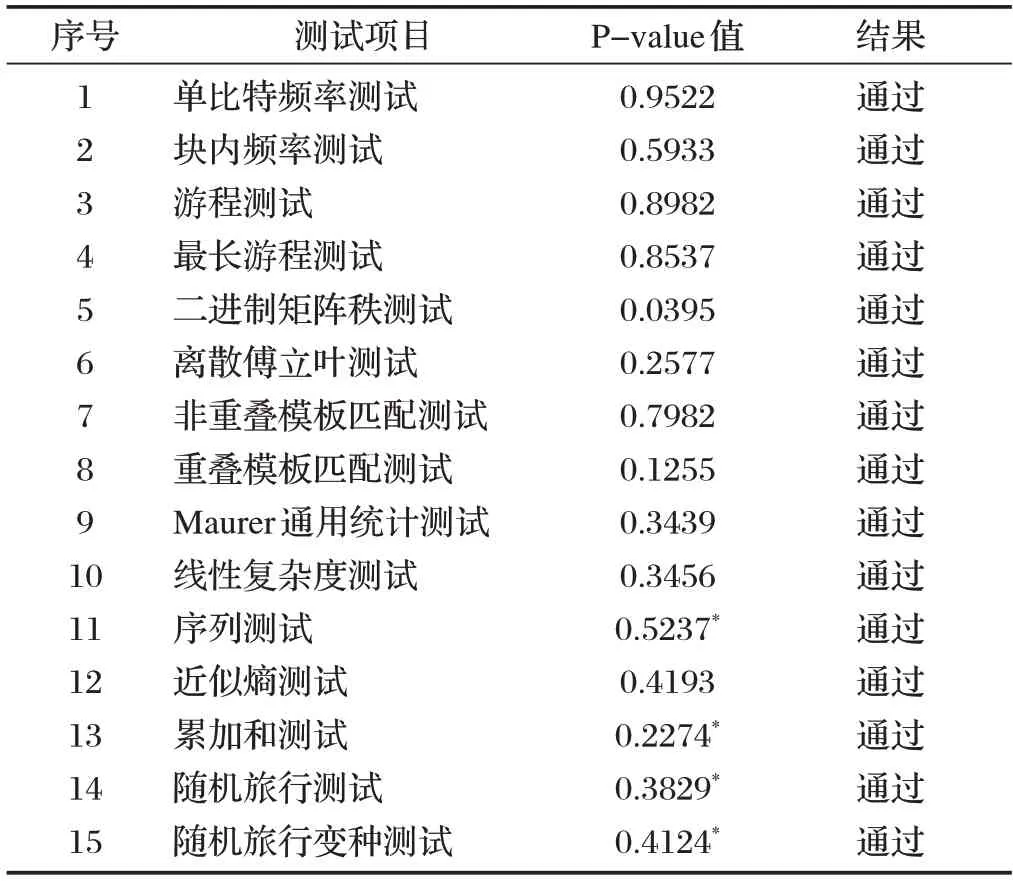
表1 NIST随机性检测结果

由表1 可知，本文的伪随机序列发生器生成的伪随机序列通过所有NIST 的SP800-22 Revision 1a 检测项目，表明本文提出的伪随机序列发生器具有良好性能指标。

3.2 密钥空间分析

本文提出的伪随机序列发生器采用2D-SLIM 和2D-LSCM 超混沌系统，音频加密方案的密钥空间为混沌系统的参数和初值空间，即2D-SLIM 的参数aϵ(0,3]、初值x ∈(-1,1)、y ∈(-1,1)，2D-LSCM的初值xϵ(0,1)、y ∈(0,1)，假设每个参数变化步长为10-14，密钥空间结果为：3 × 1014× 2 × 1014× 2 × 1014×1014× 1014=1.2 × 1071≈2236。该值大于2100，说明本文的加密方案可以有效抵抗穷举攻击。

3.3 音频数据加密仿真结果

音频数据加密仿真结果如图9(a)～图9(f)所示。图9(a)、图9(b)为音频测试数据；图9(c)、图9(d)为加密后生成的密文音频数据；图9(e)、图9(f)为解密还原后生成的明文音频数据。

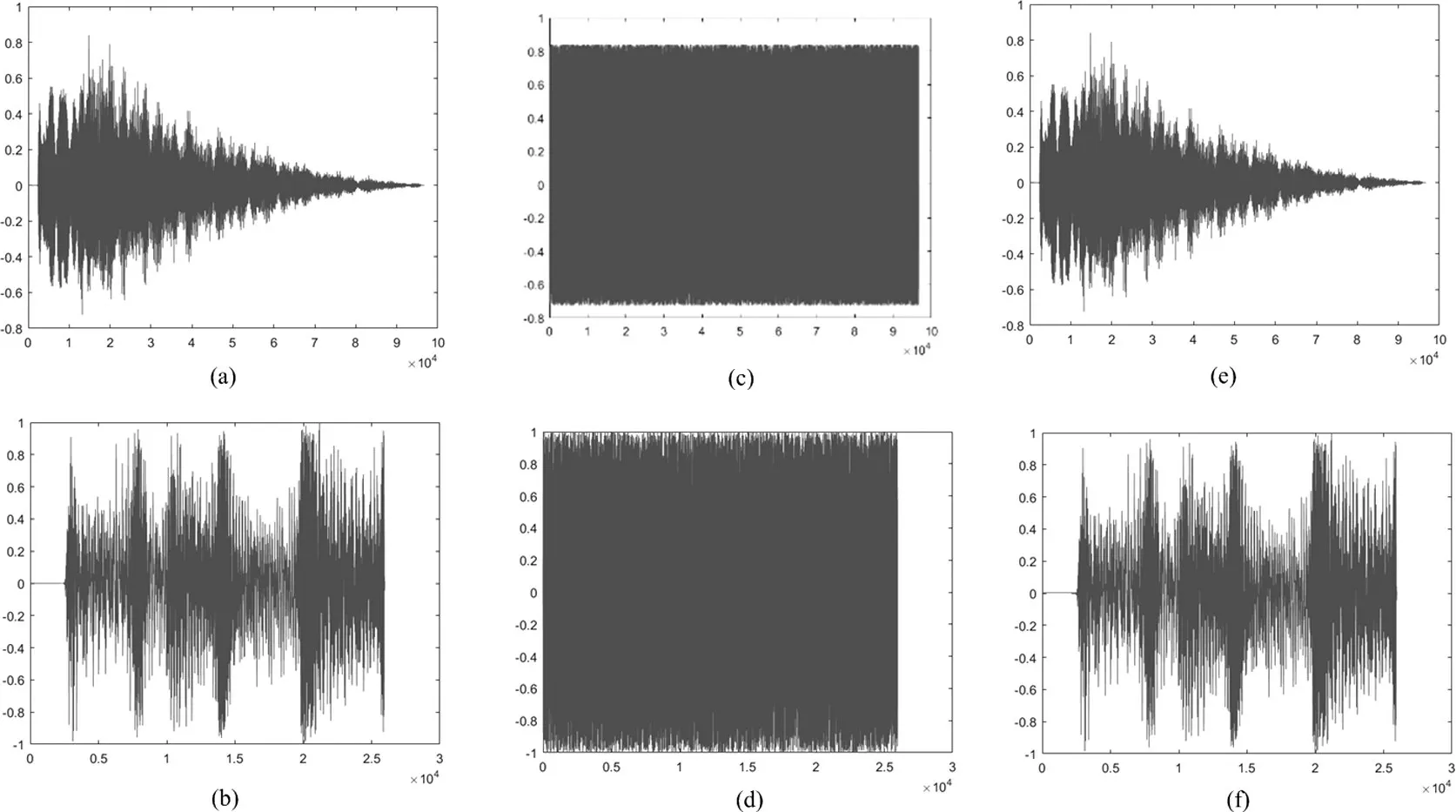
图9 音频数据加密和解密仿真示意图

图9 中的(a)为音频测试数据1；(b)为音频测试数据2；(c)为音频测试数据1 加密后的密文音频数据；(d)为音频测试数据2 加密后的密文音频数据；(e)为音频测试数据1 解密还原后的明文音频数据；(f)为音频测试数据2解密还原后的明文音频数据。音频加解密仿真结果表明，本文提出的伪随机序列发生器具有良好的性能，可以有效应用于音频数据加密场景中。

4 结论

本文基于超混沌2D-SLIM 系统和超混沌2DLSCM 系统提出了一种迭代序列耦合的伪随机序列发生器方案，该方案首先采用随机周期扰动方式防止超混沌2D-SLIM 和2D-LSCM 系统的混沌退化，随后对其迭代序列进行耦合输出，进而有效解决了由于有限精度下的混沌退化问题导致的伪随机序列周期性问题，并以此为基础构建伪随机序列发生器模型。随后采用NIST 的SP800-22 Revision 1a 伪随机序列测试标准进行随机性检测，并通过音频加密验证。实验结果表明，通过本文方案生成的伪随机序列具有良好的随机性能。本文为有限精度混沌退化对伪随机序列发生器性能影响给出了新的解决思路。