融合随机森林与多变量灰色的道路交通事故预测模型研究＊

田振中 樊丽花 董海隆 河南警察学院

引言

随着我国机动车数量的快速增长，社会机动化水平不断提高，导致道路交通事故频发，交通安全形势十分严峻。根据《中国统计年鉴2022》数据显示，2021年全国共发生道路交通事故273098起，造成62218人死亡、281447人受伤、直接经济损失145035.9万元。居高不下的交通事故不仅给人民群众的生命财产造成了巨大的损失，也影响到社会治安稳定，已经成为一个突出的社会问题。定量研究交通事故的影响因素及变化趋势，对进一步完善交通安全预防措施、推动道路交通安全治理体系和治理能力现代化建设具有重要意义。

目前，对于道路交通事故预测方法主要有三次指数平滑法、回归预测模型法、灰色预测模型法等[1-3]，其中灰色预测模型法是针对“小样本、贫信息”的不确定系统进行分析和预测的有效方法。GM(1,1)模型是目前影响最大、应用最为广泛的灰色预测模型，其在医学、工业、交通等领域都有广泛的应用[4-6]。但GM(1,1)预测模型仅适用于单一时间序列的数据，未能考虑相关因素对系统变化趋势的影响。近年来，国内外学者开始探索使用多因素灰色GM(1,N)模型进行预测，该模型不仅利用历史数据建立时间序列预测模型，也能考虑外界因素的影响[7-9]。但普通GM(1,N)模型在建模机理、模型结构等方面存在一些缺陷，导致预测误差较大、稳定性不足[10-11]。

鉴于交通事故受到人、车辆、道路、环境等诸多因素的综合影响，本文借鉴已有文献的相关研究成果，采用随机森林回归模型筛选道路交通事故的主要影响因素，应用优化多维灰色预测模型OGM(1,N)对交通事故进行预测研究，旨在提高预测效果，以期为相关部门制定科学的应对措施提供参考依据。

一、常见模型

（一）随机森林模型

随机森林（Random Forest，简称RF）是一种由多棵决策树构成的机器学习算法，已被广泛应用于各种分类与回归问题。随机森林回归模型通过自助法（Bootstrap）重抽样技术，每次从原始训练样本集S={s1,s2,…,sm}有回放地重复随机抽取一个样本，一共抽取m次，生成与原训练集具有相同容量的新训练样本集合，然后对每个新训练样本进行决策树建模，随机森林回归模型的最终结果由m棵决策树输出结果的平均值决定。

随机森林模型基于误差和节点纯度可对各输入变量的重要性进行分析，具体计算公式为：

式中，VI（Variable Importance）是变量重要性得分，VI越大，表明相应的变量越重要；ntree是决策树数量；OOBE是OOB样本得到袋外误差；OOBE是对OOB样本中的某个输入变量加入噪声干扰，保持其他变量值不变，输入决策树得到新的袋外误差。

（二）多变量灰色优化OGM(1,N)模型

为GM(1,N)优化模型，简称OGM(1,N)模型（Optimizing Grey Model），其中h1(k-1)和h2为模型的线性修正项及灰色作用量[11]。

模型（3）中的参数列p=[b2,b3,…,bN,a,h1,h2]T可以用最小二乘法估计求得[11]，有：

模型（4）的近似时间响应式为：

二、RF-OGM(1,N)组合模型的道路交通事故预测分析

（一）交通事故影响因素的选择

交通事故的影响因素众多，本文根据已有文献[2,4,12]和数据的可获得性，以每年道路交通事故发生数X1（起）为系统特征序列，从人、车辆、道路、环境等方面初步筛选国内生产总值X2（亿元）、公路货运量X3（万吨）、公路客运量X4（万人）、总人口数X5（万人）、民用汽车拥有量X6（万辆）、公路通车里程X7（万km）及机动车驾驶人数量X8（万人）7个相关因素序列进行分析。本研究通过查阅2011～2021年《中国统计年鉴》，收集交通事故发生次数和影响因素变量的相关数据。

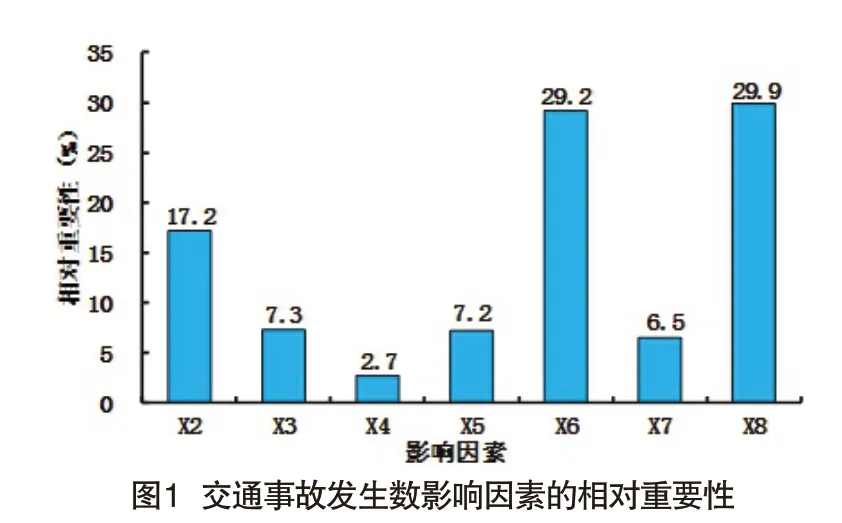
这里采用MATLAB2017a实现随机森林TreeBagger参数优化，最终选定决策树棵数、决策深度的最优超参组合为200和10，模型的PseudoR2为0.96，表明模型具有较高的拟合优度。基于随机森林特征重要性评估，计算各输入因素变量的相对重要性，结果如图1所示。由图1可知，随机森林回归下影响交通事故因素的重要性排序为：机动车驾驶人数量＞民用汽车拥有量＞生产总值＞货运量＞人口数＞公路通车里程＞客运量。其中，机动车驾驶人员数（29.9%）和民用汽车拥有量（29.2%）呈现较高相对重要性，是造成交通事故的主要因素，在OGM(1,N)模型建模时需要作为自变量导入。

（二）OGM(1,N)模型计算过程

选取上述影响较大的因素作为主要因子，构建道路交通事故发生数与机动车驾驶人数量和公路通车里程之间的OGM(1,3)模型，根据式（2）至式（5），使用MATLAB 2017a编程计算得到2011～2020年交通事故的模拟值及误差，同时为了比较OGM(1,3)模型的模拟性能，这里也构建了交通事故的GM(1,1)。OGM(1,3)模型与GM(1,1)模型的模拟值及误差，见表1。

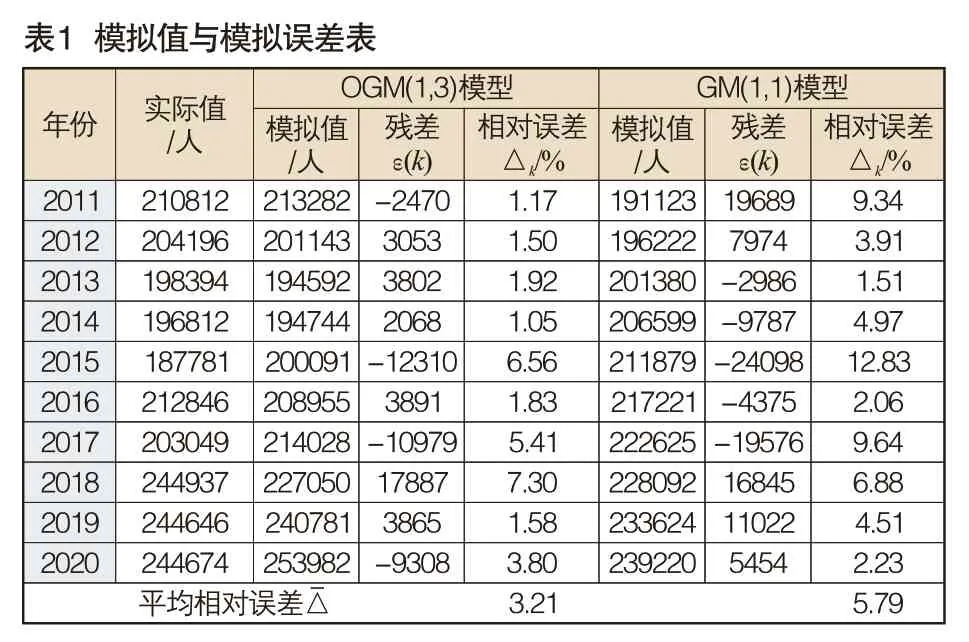
表2中GM(1,1)模型参数及符号ε(k)、△k及的含义如下：

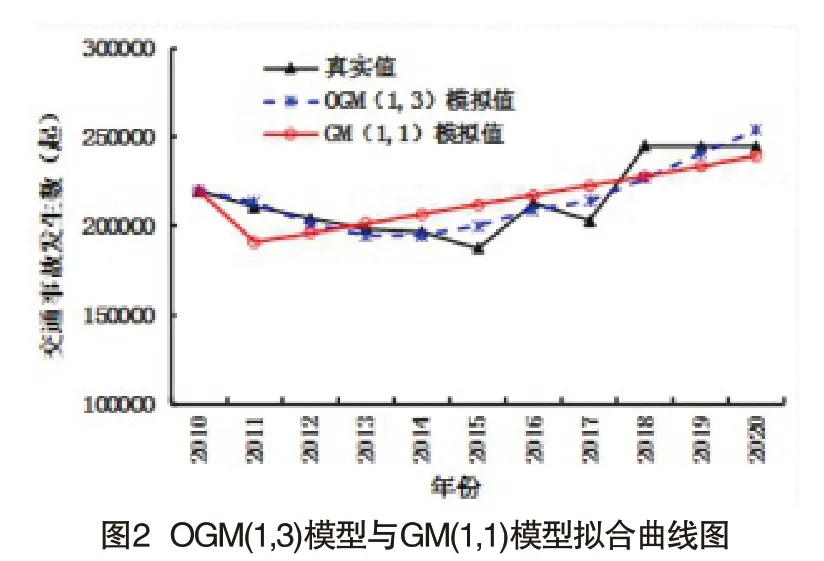
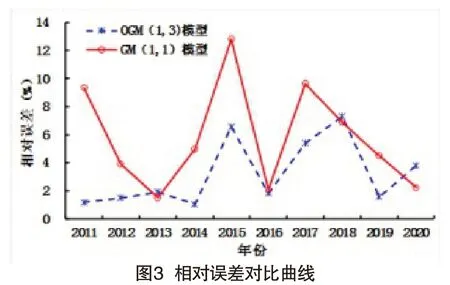
根据表1可知，OGM(1,3)模型的模拟误差为3.21%，而GM(1,1)模型的模拟误差为5.79%，表明OGM(1,3)模型具有优于GM(1,1)模型的模拟性能。为了直观表示上述两个模型对交通事故发生数的模拟效果，应用EXCEL绘制了不同模型预测值及相对误差，见图2和图3。根据图2和图3可以看出，OGM(1,3)模型模拟数据与真实值基本吻合，相对误差值波动幅度相比于GM(1,1)模型较小，最大值为7.30%，这再次表明该模型模拟效果较好，可以很好地揭示我国交通事故的动态变化规律；而GM(1,1)模型本质上是指数函数，具有严格单调性，难以实现对随机波动数据序列的有效模拟。

三、应用验证

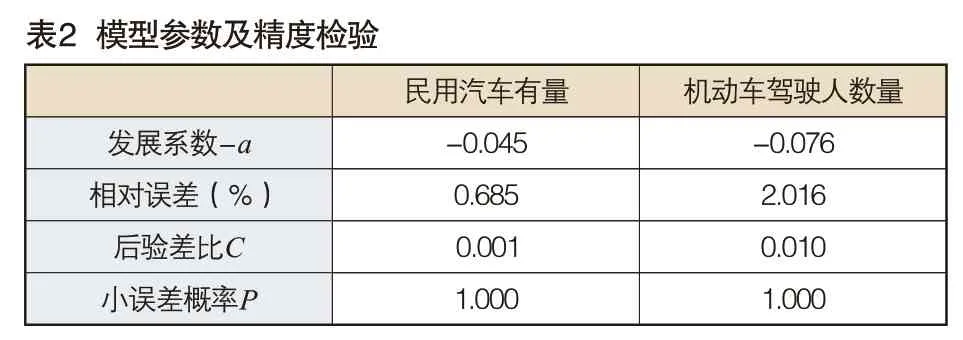
为了预测2021～2025年我国交通事故发生数，首先使用GM(1,1)模型对输入因子X6和X8的未来值进行预测，这里使用MATLAB对GM(1,1)模型进行参数估计及预测（见表2和表3），发展系数-a均小于0.3，模型精度等级均为一级（好）[13]，这说明建立的GM(1,1)模型均可用于交通事故的中长期预测；然后将各输入因子的预测值代入上述GM(1,3)模型对2021～2025年道路交通事故发生数进行预测，具体结果见表3最后一列。

由《中国统计年鉴2022》可知：2021年我国道路交通事故发生数为273098起，OGM（1,3）模型预测值为272365起，预测精度为：

而用GM(1,1)模型预测2021年我国道路交通事故发生数为244881起，预测精度为：

显然，△OGM(1,3)＞ △GM(1,1)，OGM(1,3)模型具有比GM(1,1)模型更好的预测性能，这表明融合随机森林与OGM(1,N)的预测模型适合我国道路交通事故预测。另外，从表3可以看出，我国道路交通事故发生数在未来仍将维持增长态势，到2025年交通事故发生数达到364575起，相比2021年的实际值要增加90000多起，因此道路交通安全管理和交通事故预防工作仍需进一步加强。为了推动全国道路交通安全工作高质量发展，应进一步加强道路交通安全宣传教育工作，增强全民交通安全意识，特别是要加强行业培训，提高驾驶员综合素质；进一步加大车辆检查、检修力度，确保车辆转向、制动、轮胎、线路等关键部件状况良好，加快研发并推广应用新安全技术，特别是要研究构建车路协同安全体系，不断提升车辆的智能化水平及安全性；进一步加大对道路交通基础设施建设的财政投入力度，完善道路交通安全设施，努力打造良好交通出行环境，从而有效预防和减少道路交通事故发生，加快推进我国道路交通安全治理体系和治理能力现代化建设。

四、结语

交通事故是一个严重的社会问题，受到人、车辆、道路、环境等多方面因素的影响，是各种因素综合作用的结果。本文根据已有相关文献，基于我国2010～2021年间道路交通事故发生数量及相关影响因素数据，采用随机森林算法分析道路交通事故发生数量的主要影响因素，建立了道路交通事故发生数量的多维灰色系统预测模型，在此基础上对我国2011～2021年道路交通事故发生数量进行了模拟和预测，结果显示模型预测误差较小，且预测稳定性得到提高，可以作为道路交通事故发展趋势的有效预测模型。本文的研究成果为道路交通事故发生数量影响因素分析与预测模型构建提供了一种有效的建模方法，这对于公安机关决策者制定交通管理政策、助力道路交通的安全性和运行效率提升、推动道路交通安全工作高质量发展等方面，具有一定的积极意义。