低秩Toeplitz 张量的高精度随机填充算法

温瑞萍 李文韦

(太原师范学院数学与统计学院,晋中,030619)

1 引言

由于张量在多模态结构信息表中具有优势,所以对张量的研究成为近些年来的热点问题.一个已经引起学界高度关注的现象是: 在张量数据的采集、存储、传输与处理等环节,常常会发生数据的丢失或腐蚀,因此张量数据的填充与恢复问题的研究就尤为重要.低秩张量填充问题作为低秩矩阵填充问题的推广,主要是根据已知的部分张量数据信息来填充其未知或缺失的数据.张量填充方法已经广泛应用于图像处理[1]、数据挖掘[2]、信号处理[3]及机器学习[4]等领域.低秩张量填充的数学模型一般为:

类似于矩阵填充的秩极小化模型,问题(1.1)属于非凸优化模型,是NP 难问题.如果待填充张量C的秩已知或容易估计,一些学者提出了类似于求解矩阵填充秩极小化模型的解法,但填充效果不甚理想.因而,在实际处理中,通常用逼近张量T的一个最紧凸包‖T‖*来代替rank(T),将问题(1.1)转化为下列凸优化模型,即张量填充的核范数极小化数学模型:

其中‖·‖*表示相应张量的核范数.

求解(1.2)通常的作法是将张量按照不同的模展开成矩阵,对矩阵进行填充操作后再折叠复原回张量形式.针对矩阵填充的核范数极小化问题求解,常见的经典算法有: Toh 等学者提出的加速近端梯度(APG)算法[5];Cai 等提出的奇异值阈值(SVT)算法[6];Lin 等提出的增广拉格朗日乘子(ALM)算法等[7].因为张量的分解方式有CP 分解、Tucker 分解、张量链分解、张量环分解和t-SVD 分解等[8],所以张量填充问题的求解要比矩阵填充问题的求解复杂得多.根据各种分解,许多学者提出了求解问题(1.2)的有效方法.比如,Kolda 等提出了高阶SVD 算法[9].Gandy 等提出了采用ADM 的框架求解低秩稀疏张量恢复问题[10].Liu 等基于Tucker 分解提出了三种张量填充方法[11]: 利用松弛技术,采用块坐标下降(BCD)方法求全局最优解的简单低秩张量填充算法(SiLRTC);将原非光滑问题转化为光滑问题,进而求解张量迹范数极小化问题的快速低秩张量填充算法(FaLRTC);在SiLRTC 算法的基础上应用交替方向乘子方法的高精度低秩张量填充算法(HaLRTC).

由于待填充矩阵往往具有特殊结构,Toeplitz 矩阵填充问题近年来受到许多学者的关注.比如,王川龙等提出了Toeplitz 矩阵填充的均值算法[12]、修正的增广拉格朗日乘子算法[13]、保结构算法[14]、子空间算法[15]等.温瑞萍等提出了求解Toeplitz 矩阵填充问题的逐步结构化增广拉格朗日乘子算法[16]、l步结构化增广拉格朗日乘子算法[17]、均值修正增广拉格朗日乘子算法[18]及尾端修正增广拉格朗日乘子算法[19].同样地,在张量填充的某些应用问题中,虽然待填充数据表的规模很大,但是填充问题本身往往具有对称,Hankel 及Toeplitz 等特殊结构,因而,结构化张量的填充和恢复在实际问题中的应用是很有意义且非常必要的.诸如,Badeac 等针对Hankel 张量、对称张量、Toeplitz 张量填充问题分别提出了奇异值分解快速算法[20];聂家旺等学者讨论了Hankel 张量分解和秩,证明了Hankel 张量的CP 秩、对称秩及Vandermonde 秩的一致性[21];王川龙等提出了一种快速且具有较高精度的Hankel 张量填充算法[22].

本文采用HaLRTC 算法[11]求解Toeplitz 张量填充问题,即当(1.2)中的待填充张量C恰好具有Toeplitz 结构时的情形.由于HaLRTC 算法在N次迭代的每一步均包括了需要较大计算花费的奇异值分解(SVD),本研究主要从以下两个方面改进它以降低其每次迭代中计算奇异值分解的代价: 一方面是利用具有特殊结构的Toeplitz 张量的快速奇异值分解方法,缩减奇异值分解的时间;另一方面是应用随机化思想,将在每一步迭代需按全部模展开Toeplitz 张量的操作改进为按第n模随机展开一次,减少奇异值分解的次数,从而达到提高算法效率的目的.最后通过数值实验验证改进算法的有效性.

2 预备知识

定义2.1(奇异值分解(SVD),[23])如果秩为r的矩阵A∈Rm×n的全部非零奇异值依次为σ1≥σ2≥···≥σr ＞0,则A的奇异值分解定义为:

其中U=[u1,u2,...,ur]∈Rm×r和V=[v1,v2,...,vr]∈Rn×r分别为矩阵A的前r个左、右奇异向量构成的列正交矩阵.

的矩阵称为一个n×n的Toeplitz 矩阵.

显然,T由其第一行和第一列决定,共有t-n+1,t-n+2,...,tn-1至多2n-1 个互异元素,它们分布于T的2n-1 条对角线上.若用l表示Toeplitz 矩阵对角线的指标,则有l ∈{-n+1,-n+2,...,n-1}.相应地,Toeplitz 矩阵填充问题的元素采样指标集Ω⊂{-n+1,-n+2,...,n-1}.用diag(T,l)表示Toeplitz 矩阵T的第l条对角线元素构成的向量,则

定义2.4(Toeplitz 均值结构化算子,[12])对于任意矩阵X=(xij)∈Rn×n,Toeplitz 均值结构化算子T定义如下:

其中,

可见,T(X)是由矩阵X派生的Toeplitz 矩阵,即任意矩阵都可以通过结构化算子T(·)转化为一个Toeplitz 矩阵.

则称X为Toeplitz 张量.

类似于矩阵的情形,将任意张量X进行Toeplitz 结构化的运算表示为Γ(X)=T.

3 Toeplitz 张量的填充算法

本节将文献[11]给出的高精度低秩张量填充算法(算法3.1)进行修改,应用于求解模型(1.2)中的待填充张量C恰好具有Toeplitz 结构的低秩Toeplitz 张量填充问题(算法3.2).

算法3.1 高精度低秩张量填充算法(High-accuracy Low Rank Tensor Completion Algorithm,HaLRTC)[11]

初始化:给定下标集合Ω,参数ϵ,ρ0,t,X0=PΩ(C),Yi,0=0,k:=0;

第1 步:计算

end for;

第2 步:计算

第3 步:若‖Xk+1-Xk‖F/‖Xk‖F ＜ϵ,则停止迭代,否则,转第4 步;

第4 步:计算Yi,k+1=Yi,k-ρk(Mi,k+1-Xk+1),ρk+1=tρk,k:=k+1,转第1 步.

算法3.2 高精度低秩张量随机填充算法(High-accuracy Low Rank Tensor Random Completion Algorithm,HaLRTRC)

初始化:给定下标集合Ω,参数ϵ,ρ0,t,X0=PΩ(C),Yi,0=0,k:=0;

第1 步:随机生成一整数i=randperm(N,1),并计算

第2 步:令Ti,k+1=Γ(Mi,k+1);

第3 步:计算

第4 步:若‖Xi,k+1-Xi,k‖F/‖Xi,k‖F ＜ϵ,则停止迭代,否则,转 第4 步;

第5 步:计算Yi,k+1=Yi,k-ρk(Ti,k+1-Xi,k+1),ρk+1=tρk,k=k+1,转 第1 步.

算法3.1 与算法3.2 的主要区别在于算法3.2 利用张量结构的同时应用了随机思想.将算法3.1 的每步迭代中张量按每个n模展开修改为算法3.2 中的张量随机地仅按某一k模展开一次.虽然算法的迭代步数和计算复杂度有所增加,但是避免了算法3.1 每步迭代中N次展开后带来的奇异值分解计算量,进而体现出算法3.2 在计算时间上具有优势.结构化张量不仅在数据传输和算法中能够减少存储空间,而且在算法中每次迭代均可保持Toeplitz 结构.这一方面提高了迭代矩阵的精度,另一方面可以用快速算法进行结构化矩阵的奇异值分解.

4 收敛性分析

引理4.1由算法3.2 产生的序列{Yi,k+1}是有界的.

由算法3.2 的第5 步可得

此外,

再由算法3.2 的第2 步可知

再由文献[7] 中引理1 和引理4 可得Yi,k+1=Yi,k -ρk(Ti,k+1-Xi,k+1)∈∂‖Ti,k+1‖*.令Ti,k+1=UΣVT.再由文献[6]可知

因此,

所以序列{Yi,k+1}是有界的.

令(T *,X*)为问题(1.2)的最优解,Y*是文献[7]中的对偶问题的最优解.我们首先证明

所以(4.1)式成立.

类似于文献[7]中定理2 的证明即可得T *是(1.2)的最优解.

根据文献[20],可得下列平凡的结论.

定理4.2设M∈Γ(M)是Toeplitz 张量.则对于任意的Toeplitz 张量Y,有

定理4.3设Ti,k+1是在算法3.2 中由Mi,k+1所生成的Toeplitz 张量.则有

其中T *是问题(1.2)的最优解.

证明由于

5 数值实验

本节通过数值实验验证算法3.1 与算法3.2 的有效性.实验包括两个部分: 分别利用T-HaLRTC与T-HaLRTRC 算法求解Toeplitz 张量填充问题及分别利用MT-HaLTRC 与MT-HaLRTRC 算法求解Toeplitz 均值张量填充问题.所有数值实验均在戴尔(DELL)PowerEdge R740xd 高性能2U 机架式并行计算服务器上,MATLAB(R2019b)环境下运行实现.从算法的迭代步数、CUP 总的计算时间(单位: 秒(s))及精度三个方面进行比较.

在实验中,p表示采样率,参数αi=,ρ0=10-7,其余参数均采用文献[11] 的建议.另外,利用随机方法生成秩不同且维数分别为50×50×50,100×100×100,150×150×150,200×200×200,250×250×250 和300×300×300 且秩为(10,10,10)的Toeplitz 张量和Toeplitz均值张量.

5.1 Toeplitz 张量

两种算法在采样率分别为0.6,0.5,0.4,0.3,0.2 时的实验结果分别见表1 至表5.下文中X*表示输出的Toeplitz 张量,C为原始的Toeplitz 张量;加速比SP 和相对误差RSE 的计算式如下:

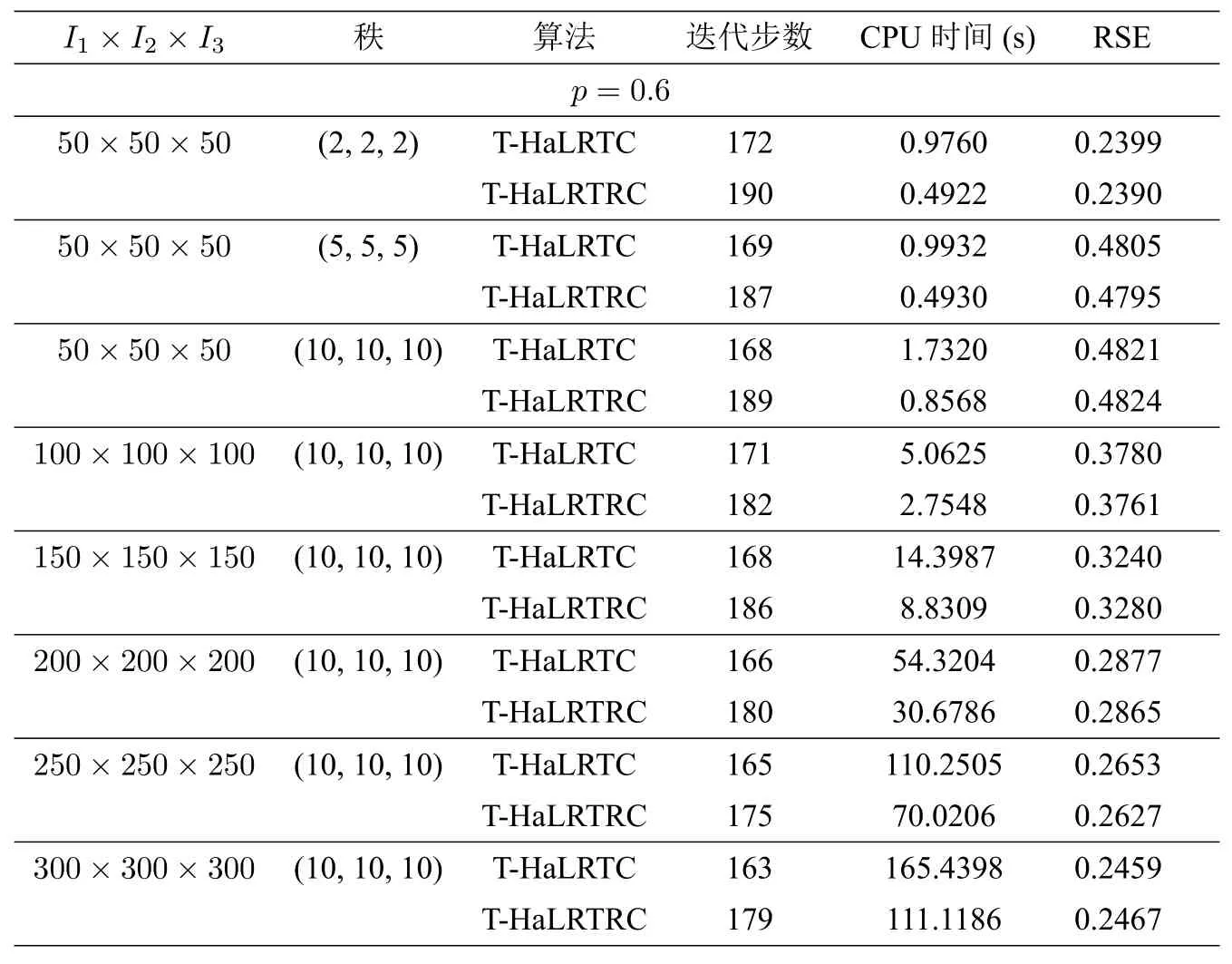
表1 当p=0.6 时,算法T-HaLRTC 和T-HaLRTRC 的比较

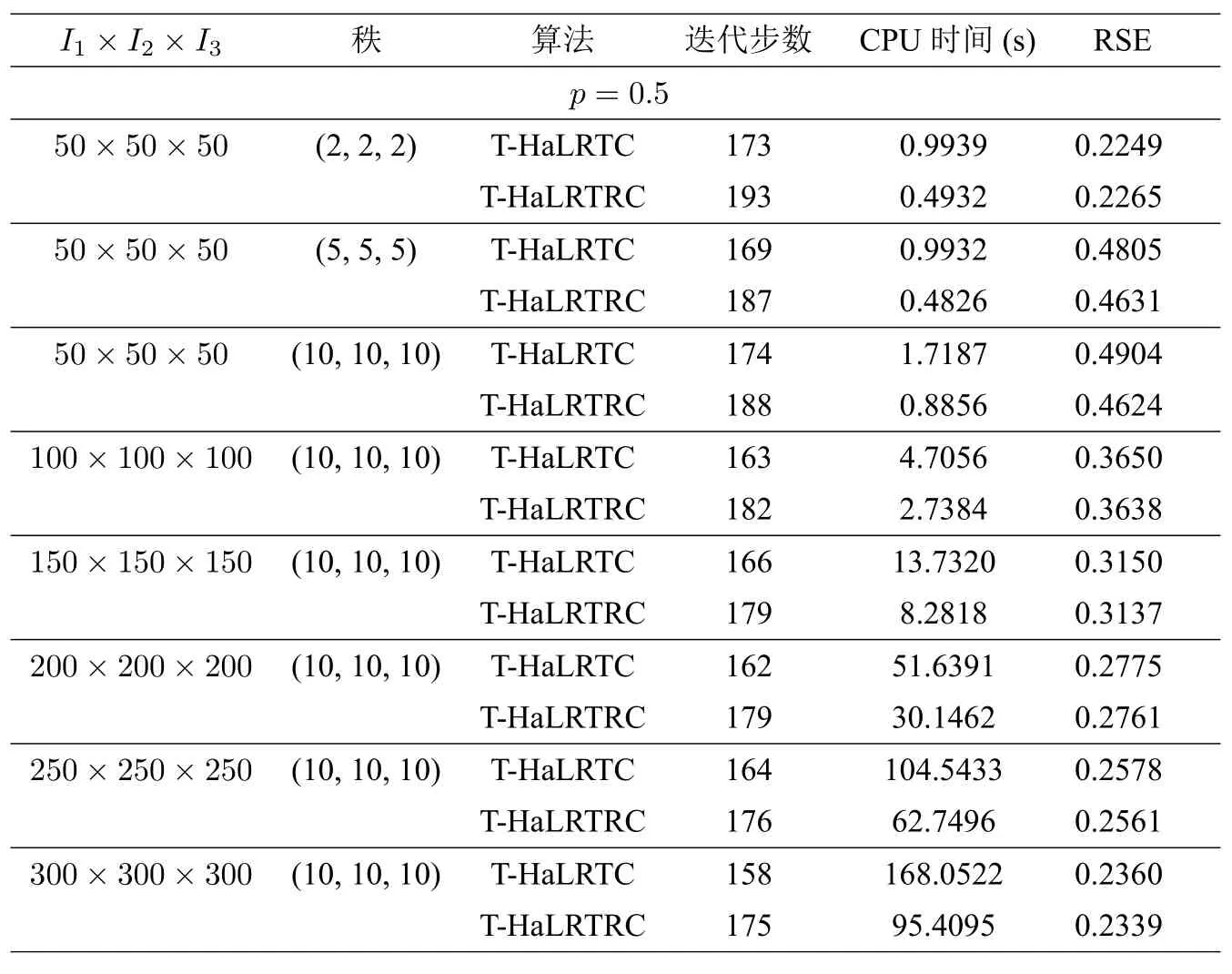
表2 当p=0.5 时,算法T-HaLRTC 和T-HaLRTRC 的比较

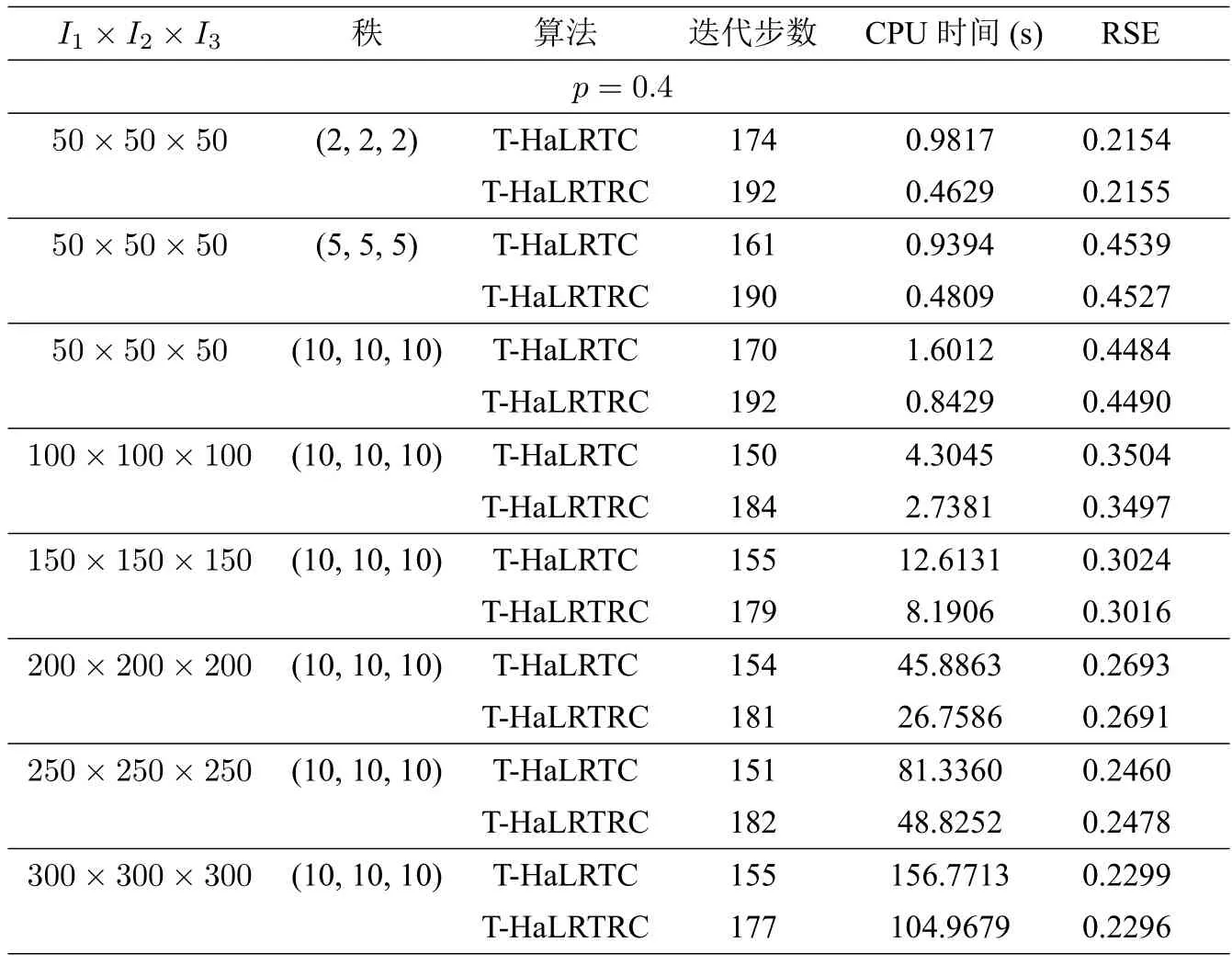
表3 当p=0.4 时,算法T-HaLRTC 和T-HaLRTRC 的比较

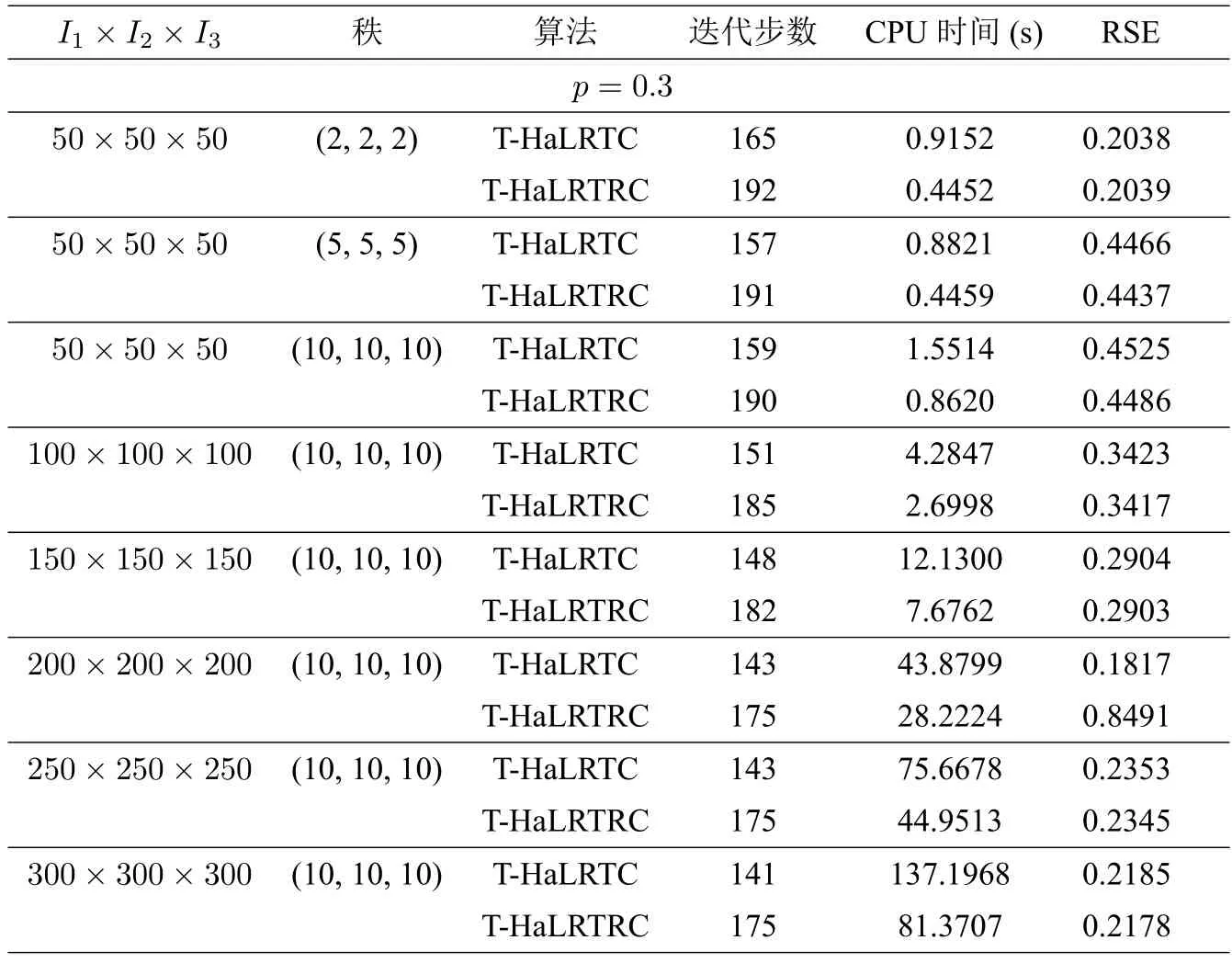
表4 当p=0.3 时,算法T-HaLRTC 和T-HaLRTRC 的比较

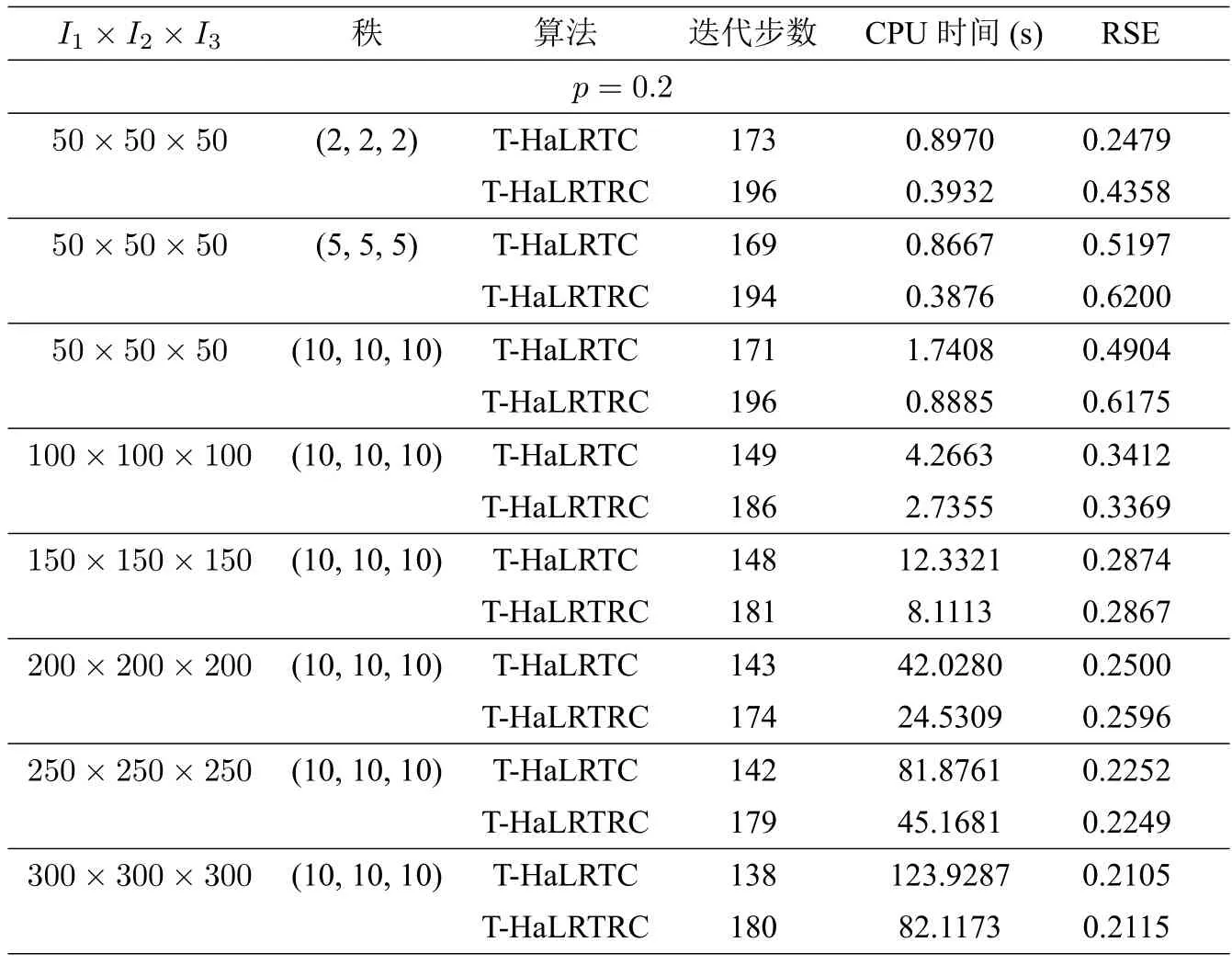
表5 当p=0.2 时,算法T-HaLRTC 和T-HaLRTRC 的比较

包括[11] 在内的文献中的数值实验,通常只针对max{I1,I2,I3} 小于或等于100 的张量数据进行数值测试,而本文的数值实验规模达到了I1=I2=I3=300.由表1 至表5 可知,在采样率p ∈{0.2,0.3,0.4,0.5,0.6}时,T-HaLRTC 算法与算法3.2 均收敛,两个算法都满足了规定的停止准则.虽然新算法3.2 的迭代步数总是大于T-HaLRTC 算法的迭代步数,但是由于嵌入Toeplitz 结构化操作,使得精度提高,而且加入随机思想减少了奇异值分解的计算量,从而总的运行时间显著地缩短,新算法3.2 比T-HaLRTC 算法花费更少.特别是当张量的采样率较小而秩比较大的时候,算法3.2 更彰显优势,其加速比高达约50%.

此外,两个算法的计算时间比较图(图1)更加直观地体现了新算法的有效性,其中图1 (a),(b),(c),(d)分别显示在不同采样率下,T-HaLRTC 算法与T-HaLRTRC 算法在不同维数且秩为(10,10,10)时对应的CPU 耗时.从图1 可知,T-HaLRTRC 算法的CPU 时间显著少于T-HaLRTC 算法的CPU时间,表明T-HaLRTRC 算法比T-HaLRTC 算法在总计算代价方面更具有优势.

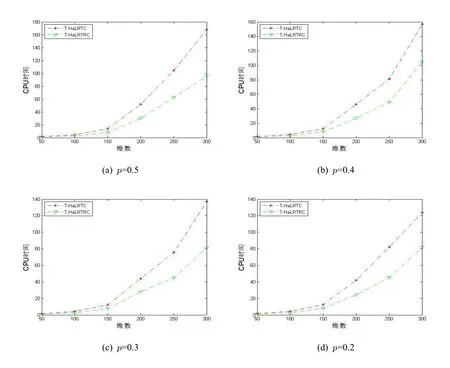
图1 不同采样率下T-HaLRTC 算法与T-HaLRTRC 算法时间的比较

5.2 Toeplitz 均值张量

本小节针对Toeplitz 均值张量,在采样率分别为0.5,0.4,0.3,0.2 时对两种算法进行比较,实验结果见表6 至表9.本小节针对Toeplitz 均值张量也进行了大量的数值实验.同5.1 节的情形,实验规模达到了I1=I2=I3=300.

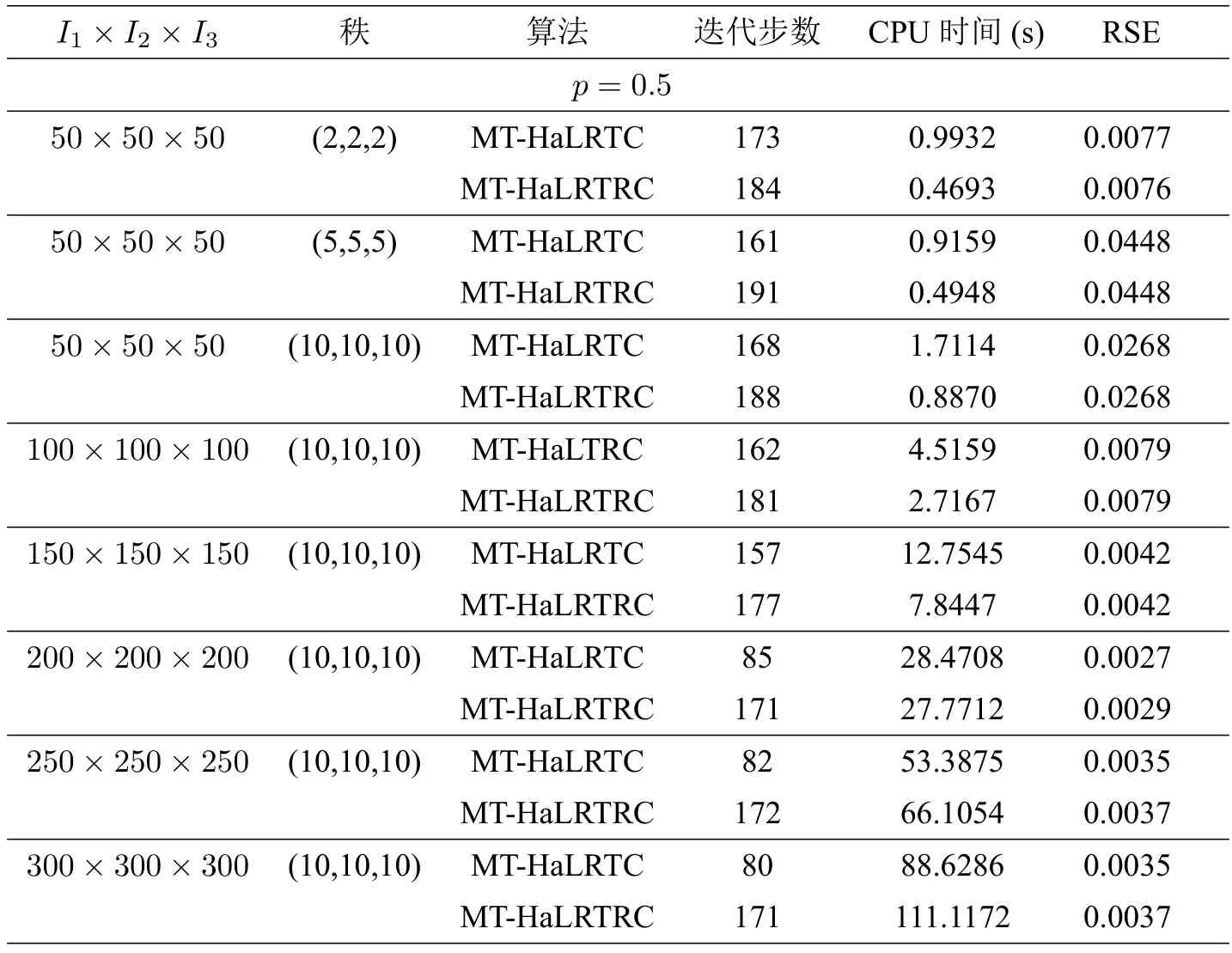
表6 当p=0.5 时,算法MT-HaLRTC 和MT-HaLRTRC 的比较

表7 当p=0.4 时,算法MT-HaLRTC 和MT-HaLRTRC 的比较

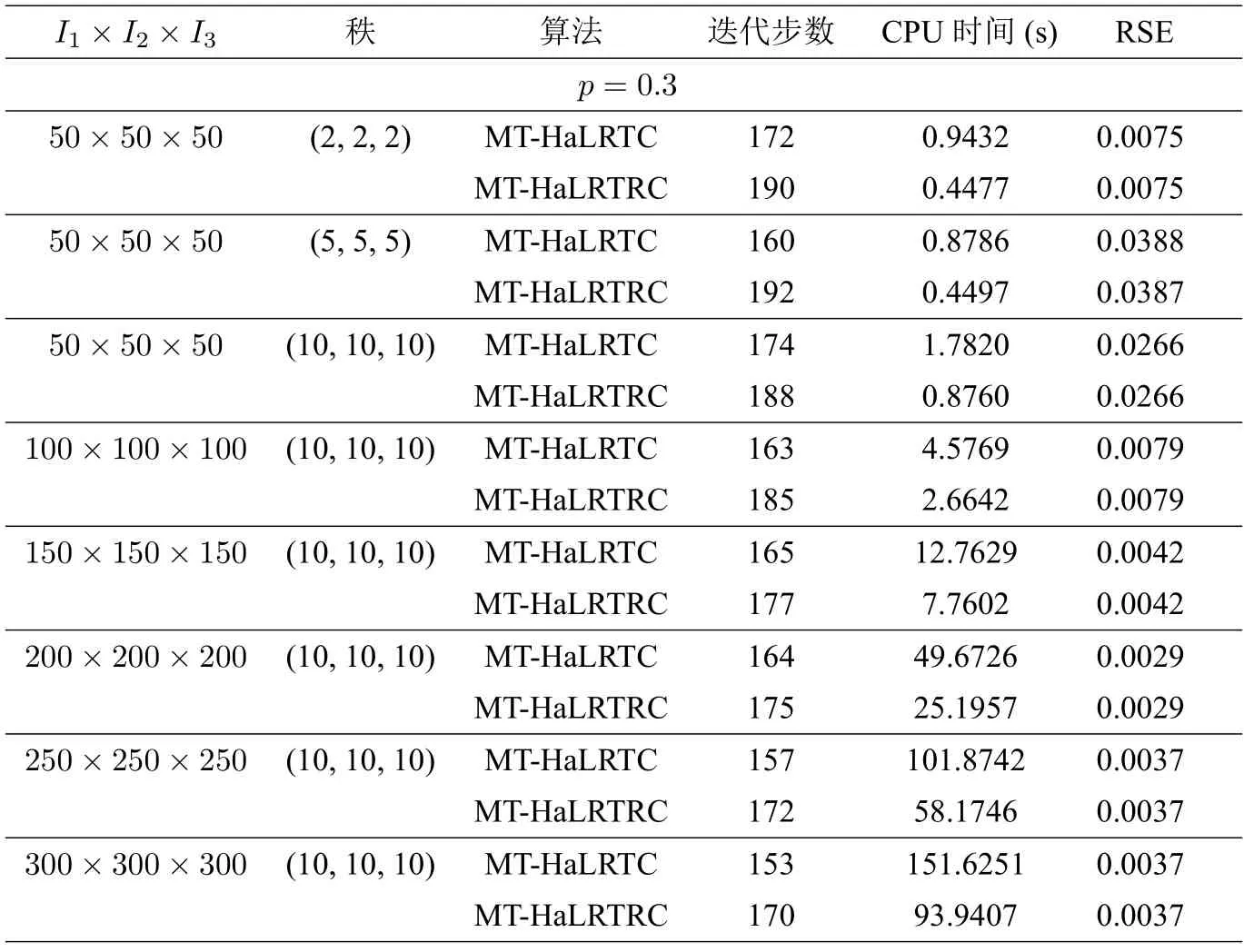
表8 当p=0.3 时,算法MT-HaLRTC 和MT-HaLRTRC 的比较

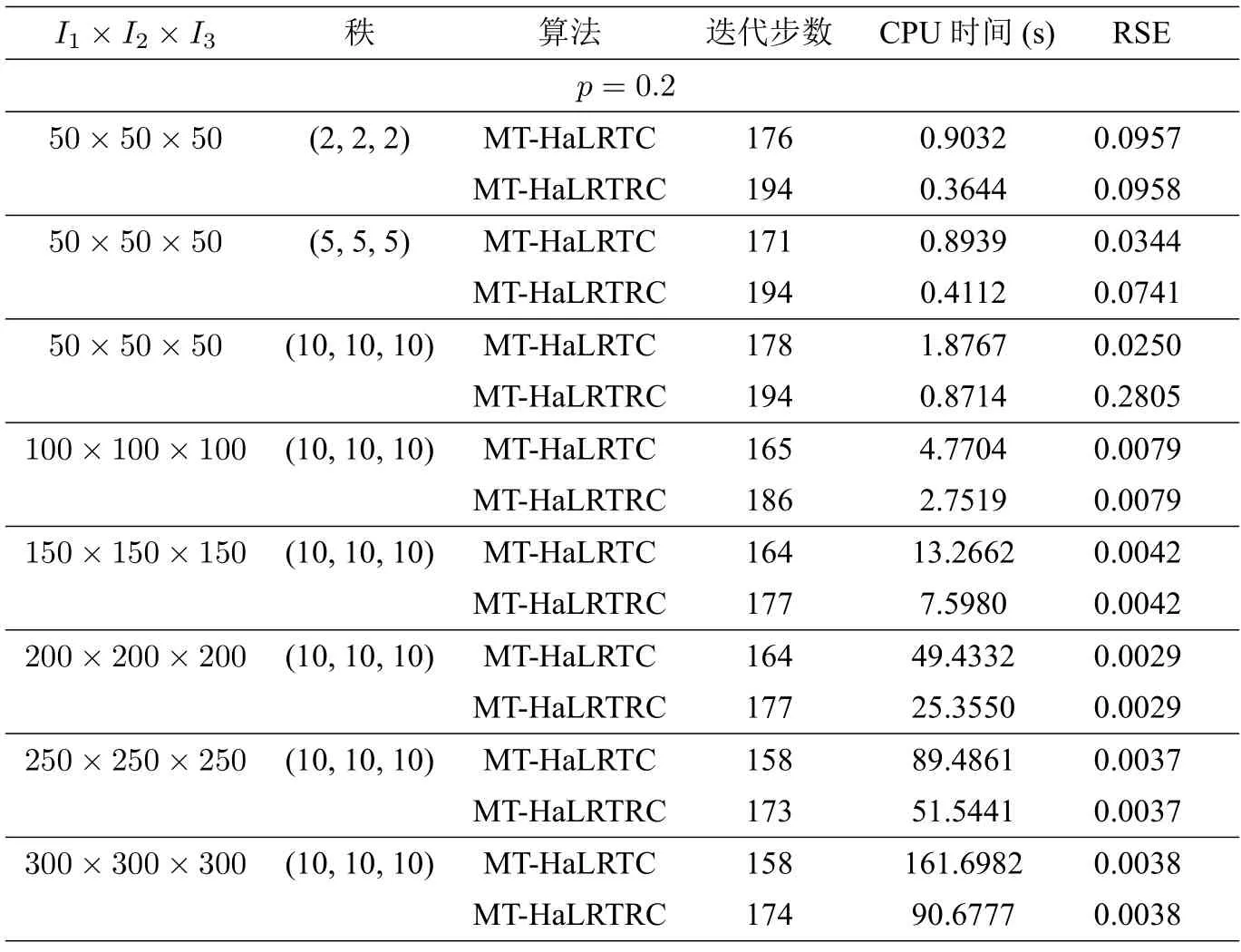
表9 当p=0.2 时,算法MT-HaLRTC 和MT-HaLRTRC 的比较

从表6 至表9 可以看出,在采样率p ∈{0.2,0.3,0.4,0.5}时,MT-HaLRTC 算法与本文的新算法3.2 均收敛,均达到了规定的停止准则.这表明两种数值算法都具有较好的稳定性.虽然增加了随机思想的算法3.2 的迭代步数总是大于MT-HaLRTC 算法的迭代步数,但是在引入随机思想的同时嵌入了Toeplitz 结构化操作,这不仅使得精度提高,而且降低了计算量,从而总的运行时间明显缩短,特别是当张量的采样率较小(这意味着原始的已知数据很少) 而秩比较大的时候,优势更加显著,其加速比高达50%.

图2 直观地体现了新算法的有效性,其中,(a),(b),(c),(d) 分别显示了在不同采样率下,MT-HaLRTC 算法与MT-HaLRTRC 算法在不同规模且秩为(10,10,10) 时对应的CPU 耗时.图2 表明MT-HaLRTRC 算法比MT-HaLRTC 算法在总计算花费方面更具有优势.

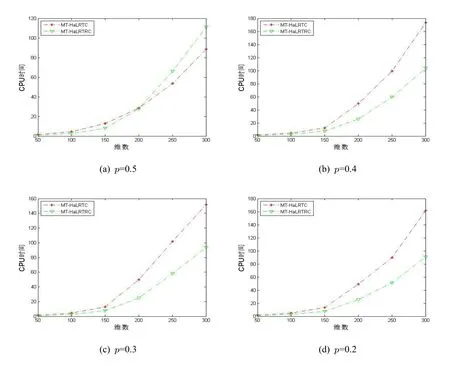
图2 不同采样率下MT-HaLRTC 算法与MT-HaLRTRC 算法时间的比较

6 总结

本文通过在高精度填充算法中引入随机思想给出了一种新算法并应用于求解低秩Toeplitz 张量与低秩Toeplitz 均值张量填充问题.新算法按预期达到了停止准则.文中给出了算法的收敛性分析,并且通过大量的数值实验验证了新算法的有效性.