基于遗传算法求解TSP问题

文/靳博文

TSP问题是一个备受研究者们关注的NP难题，遗传算法作为应用较为普遍的智能优化算法，是求解TSP问题的有效方法。本论文通过改变种群数量、交叉概率、变异概率、城市数量等参数，对比运行结果后分析得出这些参数设置的最优区间，为遗传算法解决TSP问题提供参考。

1.概述

在数学领域中，TSP问题被学者们视作是一个典型的组合优化问题[1]。该问题在生活中非常常见，很多发生在我们身边问题就是TSP问题模型在现实生活中的应用[2-4]。因此，研究TSP问题不仅具有很大的理论意义，也具有相当高的实际价值。当城市数量较少时，TSP问题很容易得到解决，然而在现实的问题中，“城市数量”往往很多，这使得该问题的解决难度大大增加。目前，在求解大规模TSP问题时，通常使用智能优化算法。本文主要聚焦遗传算法，分析不同参数设置对求解TSP问题的影响。

2.遗传算法

遗传算法起源于人类对生物系统的观察，用计算机来模拟生物遗传进化的规律进行迭代，是由Michigan大学的约翰·霍兰德(J·Holland)教授于1975年首先提出来的。按照自然界适者生存的法则，种群越优秀的个体越有更高的概率遗传自己的基因。每个个体的染色体通过选择、交叉和变异等过程产生新的更优的染色体，从而使得种群得到优化，这也意味着得到的解越来越优，种群通过这样的规则进行迭代优化，直到最终得到目标问题的最优解。遗传算法是一种全局搜索算法，当遗传算法对构建模型进行求解时，根据实际问题的初始解进行编码形成基因串，基因串即染色体经过选择、交叉、变异后形成新的染色体，新形成的染色体比之前的染色体更接近最优解。再经过不断的迭代，一直得到最优解，遗传算法的主要步骤是编码解码、确定初始种群、确定适应度函数、选择、交叉和变异。

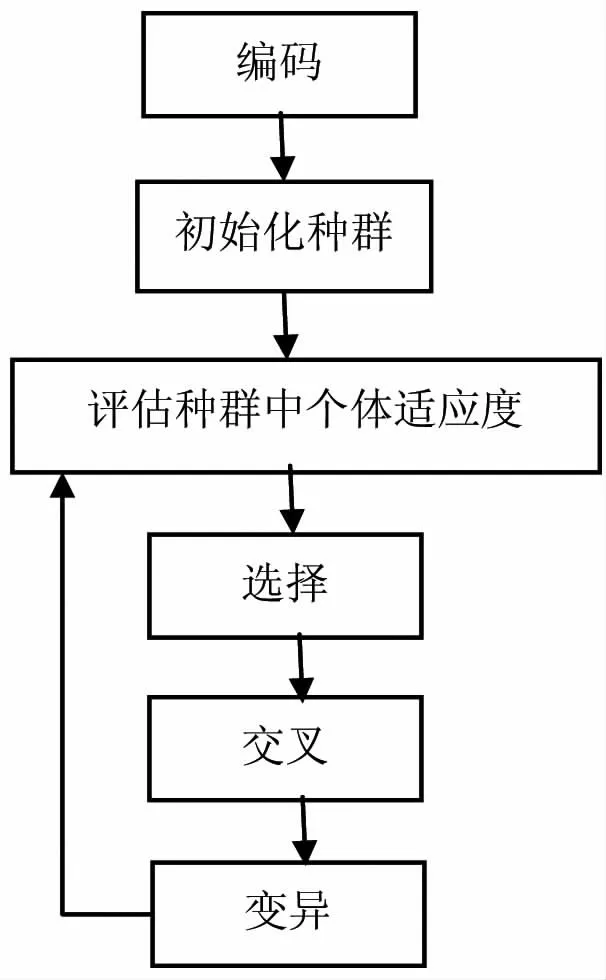
图1 遗传算法流程

3.算例仿真

为了研究只改变种群参数、交叉概率、变异概率、城市数量时，遗传算法的不同表现，做算例仿真如下。在城市数为25，迭代次数为2000，种群个数为100，交叉概率为0.8，变异概率为0.05条件下，结果如下图所示。结果图从左到右，从上到下依次为城市位置分布、初始种群分布、最终路线图、最小种群路径随迭代次数的变化图。按照上面的方法，本着控制变量的实验原则，分别运行以上述实验为基准其他参数不变，种群数量、交叉概率、变异概率、城市数量由大到小的算例仿真，并对运行结果进行比较。

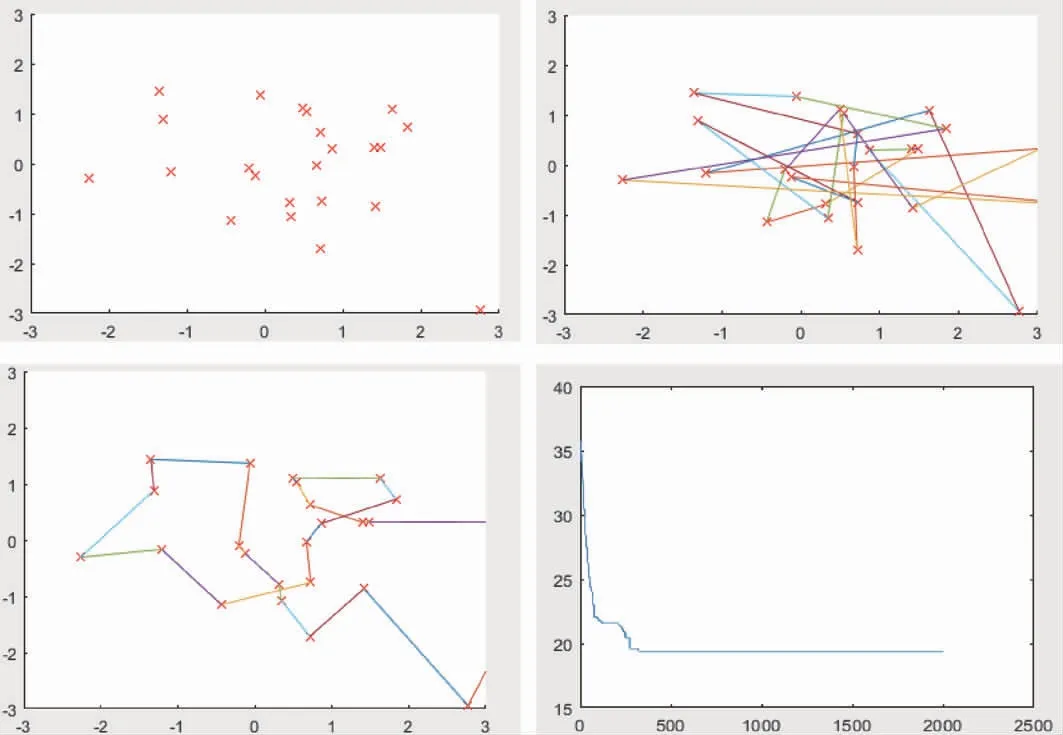
图2 运行结果图

4.结论

通过上述算例分析，可得出结论如下：（1）在种群数量改变时，随着种群数量的增加，路径总长度达到收敛的迭代次数，即达到最优解的迭代次数和最短距离，即最优解的值，变化趋势均是先下降后上升。这也意味着种群数量大小与收敛速度相关，当种群数量过大时，收敛速度会相应减缓。（2）在交叉概率改变时，随着交叉概率的增大，达到最优解的迭代次数和最优解的值变动较为频繁。（3）在变异概率改变时，随着变异概率的增大，达到最优解的迭代次数变化趋势为先增加后减少；最优解的值则随着变异概率的增加而不断增加。（4）在城市数量改变时，随着城市数量增加达到最优解的迭代次数不断增加，并且逐步趋近2000次；最优解的值也相应增加。当城市数量过大时，遗传算法在求解TSP问题方面处于劣势。