基于在线梯度下降的Mini Batch K-Prototypes算法

贾子琪, 万世昌, 张腾飞, 吉康毅, 常雪瑞

(南阳理工学院计算机与软件学院 河南 南阳 473004)

0 引言

无监督学习是机器学习领域中的一个重要分支,目标是通过发掘数据之间的内在关系来揭示数据的潜在结构和模式,包含聚类、降维、特征学习等方法。K-Prototypes算法是无监督学习经典聚类算法之一,是处理数值型数据的k-means算法与处理分类型数据的k-modes算法的融合和拓展,能够处理混合型数据。由于其简单易行、易于解释的特点,应用非常广泛。K-Prototypes算法是基于划分的聚类算法,通过相异度计算方法计算样本与簇中心的相异度进而将样本划分到所属簇中。K-Prototypes算法通过迭代的方法求簇内成本值的最小值,从而求得每个簇的中心。在每次迭代中,簇中心总是朝着成本值更小的方向优化,使成本值在这个过程中收敛到局部最小值。

K-Prototypes算法同时也存在一些不足,处理大型数据集时运行时间急剧增加;仅能收敛于局部最小值。针对K-Prototypes算法存在的不足,Ben HajKacem等将MapReduce模型与K-Prototypes算法并行化处理以使算法能够处理大型数据集[1];Byoungwook Kim等提出新的样本划分方式,并以此提出快速K-Prototypes算法(Fast K-Prototypes)[2];针对K-Prototypes算法仅能收敛于局部最小值的问题,DUC-TRUONG PHAM等人提出将蜜蜂算法(BA)与K-Prototypes相融合,使求解过程可以探索更多的空间以得到效果更好的收敛结果[3]。

近年来,大数据越来越受到人们的关注,如何让大型数据集发挥作用产生价值成为人们期盼的目标。但是诸如K-Prototypes等聚类算法应对大型数据集时却因为运行时间急剧增加的问题而不能取得良好的效果。文献[2]通过分解距离计算过程来达到减少计算时间的效果,但是每次迭代仍需要计算所有对象与每个簇中心的相异度差异,加速效果有限;文献[1]将聚类算法应用到新的操作系统上,并未改进算法程序,改进效果有待提升。所以合理改进K-Prototypes算法以提高运行效率十分重要。

为解决上述问题,论文根据在线梯度下降算法(Online Stochastic Fradient Descent Algorithm,简称OSFD),对K-Prototypes算法的迭代过程进行优化,以减少算法每次迭代所需的计算量从而降低算法的时间复杂度,提升算法运行效率,且不影响算法的收敛性和有效性。

1 相关工作

K-Ptotypes算法融合了k-means算法处理数值型数据集与k-modes算法处理分类型数据集的方法,使算法能够处理现实世界中更常见的混合型数据信息[4-5]。

给定一组包含n个对象的有限对象集合X={X1,X2,…,Xn}。其中Xi={x1,x2,…,xm}每个对象由m个特征构成,且特征中mr个为数值型特征,mc个为分类型特征,满足mr+mc=m。

定义C={C1,C2,…,Ck}为k个簇中心点的集合。其中Ci表示第i个簇的中心点,Ci={c1,c2,…,cm}且k≥2,∀i,j∈(1,k)(Ci∩Cj=φ)。K-Ptotypes算法的目标函数为

(1)

K-Prototypes算法每次迭代都需要花费大量时间来计算所有样本与每个簇中心的相异度以将其划分到簇中,这导致K-Prototypes算法在处理大型数据集时运行时间急剧增加。

2 基于在线梯度下降的Mini Batch K-Prototypes算法(GDMB K-Prototypes)

根据在线梯度下降算法对K-Prototypes算法的迭代过程进行优化,提出基于在线梯度下降的Mini Batch K-Prototypes算法(简称GDMB K-Prototypes)。GDMB K-Prototypes算法可以在不影响算法的收敛性和有效性的前提下,减少算法每次迭代所需的计算量,进而降低算法的时间复杂度,提升算法运行效率。

2.1 在线梯度下降算法(OSFD)

定义Z为变量ρ的概率空间,Sn为训练集,H为假设空间。定义损失函数V的计算公式为H×Z→R+。OSFD算法的目的是在迭代过程中求得函数I(fK)的最小值,I(fK)函数定义为

(2)

批量学习算法是将训集映射到假设空间中的函数,可表示为

fn=A(Sn)∈H

(3)

同时批量学习算法是一种递归函数,存在定义

f0=0

(4)

fn+1=A(fn,zn)

(5)

在线梯度下降算法是在线学习算法在梯度下降中的拓展,由于每次训练只针对当前样本,从而有效降低了梯度下降算法的运行成本[6]。

2.2 GDMB K-Prototypes算法

与K-Prototypes算法类似,k-means算法也是一种基于划分的聚类算法。二者每次迭代都需要花费大量时间在相异度计算上,根据相异度计算结果将所有样本划分到距离其最近的簇中心所在的簇中。这样做的弊端是在处理大型数据集时运行时间急剧增加。

D Sculley[7]基于在线梯度下降算法提出一种针对K-Means的改进算法Mini Batch K-Means算法。Mini Batch K-Means算法能够将算法运算时间降低几个数量级,适用于对延迟、可扩展性和稀疏性有较高要求的场景[8-9]。Mini Batch K-Means算法流程如表1所示。

表1 Mini Batch K-Means算法流程

受Mini Batch K-Means算法的启发,综合在线梯度下降算法与K-Prototypes算法提出基于在线梯度下降的Mini Batch K-Prototypes算法。得到每次迭代均进行小批量优化且能够处理混合型数据的GDMB K-Prototypes算法。其步骤描述如表2所示。

表2 GDMB K-Prototypes算法步骤

3 实验结果及分析

3.1 数据集描述和实验设置

为验证提出的GDMB K-Prototypes算法的有效性,使用UCI真实数据集与人工数据集Dataset1、Dataset2进行实验验证。论文选用的UCI真实数据集包括adult、Car Evaluation、connect-4和abalone。Adult数据集从1994年世界人口普查数据中摘选而来,对象数量48842个,包含受教育状况、工作状况等8个分类型数据和年龄、收入等6个数值型数据。Car Evaluation数据集对象数量1728个,从安全性能、可容纳人数等6个分类型数据评估一款汽车的优良程度。connect-4数据集通过记录connect-4游戏对局的期盼状态与对应的胜负探究两者之间的关系,对象数量67557个,由42个分类型数据描述当前棋盘状态。abalone数据集对象数量4177个,使用身体长度、宽度、重量等7个数值型数据和1个分类型数据特征来判断鲍鱼年龄。

为探究算法在不同数据规模下运行速度的变化规律,论文使用2组人工数据集进行比对实验。使用Scikit-Learn库的make_blobs函数生成簇数为3、对象数量为30000个、每个样本由2个数值型数据描述的聚类数据集。以100%、10%、1%、0.1%的比例从该数据集中等距离抽样得到与原数据集具有相同簇数量、特征数的4个人工数据集Dataset1-1、Dataset1-2、Dataset1-3、Dataset1-4,对象数量分别为30000个、3000个、300个、30个。以同样的方法生成簇数量为3、对象数量为30000个、每个样本由2个数值型数据、2个分类型数据描述的聚类数据集,等距抽样得到4个数据集Dataset2-1、Dataset2-2、Dataset2-3、Dataset2-4,对象数量分别为30000个、3000个、300个、30个。实验选用的UCI真实数据集和人工数据集的具体信息如表3所示。

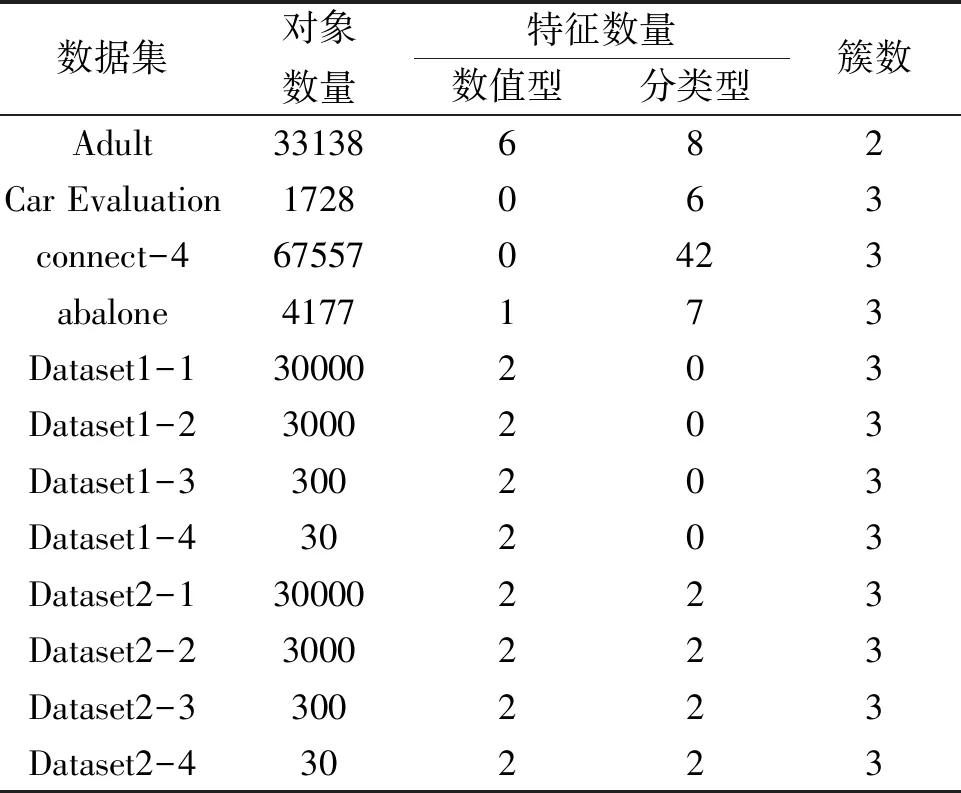
表3 实验所选数据集信息展示

算法使用Python语言实现,所有实验均使用64位Windows10家庭版操作系统。处理器为11th Gen Intel(R) Core(TM) i9-11900K @ 3.50 GHz。为确保实验的可靠性,所有实验结果均是50次重复实验取平均值。

针对改进算法运行效率的评价,论文采用直观的运行时间(T)作为评价指标。针对聚类结果精度的评价,采用聚类纯度(Purity)作为实验评价指标。聚类纯度指标是通过计算每个簇正确分类样本的数量和与总对象数量的比值来体现聚类结果的精度,Purity值越大,表示聚类结果中被正确划到对应簇中的样本比例越高,也即聚类结果精度越高。Purity值计算方法如公式(6)所示。

fn+1=A(fn,zn)

(6)

其中,n表示数据集中对象的个数,ni表示真实分类的第i个类簇中被正确分配的对象个数,cni表示聚类结果中第i个类簇的分配对象个数,pni表示真实分类中第i个类簇的对象个数。

3.2 实验结果分析

为保证对比实验的有效性,论文对一些变量因子进行控制。在对比实验中,对于随机选取初始簇中心的K-Prototypes算法、GDMB K-Prototypes算法,给出正确的目标聚类数。运行20次随机初始簇中心选择程序以确定初始簇中心,在每次试验中,每种方法都使用相同的随机初始簇中心。通过计算20次实验结果的平均值作为最终实验结果。对于K-Prototypes算法、GDMB K-Prototypes算法的权重值γ,通过γ=分类特征个数/数值特征个数给出。论文在conect-4和adult数据集的测试过程中,在保证实验结果不产生明显差异的前提下,将比例b的最小取值边界设为0.0001。

3.2.1 时间复杂度分析

K-Prototypes算法时间复杂度为O(nkt),n为对象数量,k为初始簇中心的数量,t为迭代次数。GDMB K-Prototypes算法时间复杂度为O(bnkt),n、k和t参数的含义与K-Prototypes算法相同,b为抽取样本与总样本的比例,且比例b与对象数量成反比。

3.2.2 真实数据集实验结果分析

由表4可知,改进后的GDMB K-Prototypes算法,在对象数量更大的adlut和connect-4数据集上每次迭代速度更快、迭代次数更多,因此纯度值较K-Prototypes算法更高。在对象数量较少的Car Evaluation和abalone数据集上,由于每次抽样的对象数量过少、不能准确代表簇中心的样本分布,导致聚类效果较K-Prototypes稍有下降,聚类纯度值略微降低。

表4 GDMB K-Prototypes和K-Prototypes算法在4个真实数据集上的聚类纯度与聚类时间

由表4可知,GDMB K-Prototypes算法在adult、connect-4、abalone数据集上的运行时间分别是K-Prototypes算法的6.58%、23.8%和11.43%,表明提出算法在处理对象数量更大的数据集时能显著提升算法效率,降低运行时间。Car Evaluation数据集的对象数量较少、导致K-Prototypes算法运行时间很短,优化空间不大,但GDMB K-Prototypes算法运行时间依然是前者的57.44%。

3.2.3 人工数据集实验结果分析

为探究提出算法在处理不同对象数量数据集时的表现,设计了人工数据集实验。数据集Dataset1-1、Dataset1-2、Dataset1-3、Dataset1-4拥有相同簇数、簇中心、样本特征下,以对象数量为变量,探究算法纯度值与运行时间的变化规律。数据集Dataset2的性质同理。

由表5可知,在对象数量为30、300和3000个时GDMB K-Prototypes算法的聚类纯度值与K-Prototypes算法相比持平或略有下降,总体差值在3%以内。当对象数量为30000个时GDMB K-Prototypes算法的聚类纯度值比K-Prototypes略高,这一现象是否与对象数量增长有关有待进一步实验验证。

表5 GDMB K-Prototypes和K-Prototypes算法在人工数据集上的聚类纯度与聚类时间

由表5可知,当对象数量为30、300、3000和30000个时,GDMB K-Prototypes算法运行时间分别是K-Prototypes算法运行时间的81.08%、80.56%、66.83%和55.61%。实验结果表明数据集的对象数量越大,GDMB K-Prototypes算法抽样更新簇中心的速度优势越能体现,算法优化效率更高、运行时间更快。

4 结论

实验表明,论文提出的GDMB K-Prototypes算法对真实数据集中对象数量较大的adlut和connect-4数据集聚类纯度较K-Prototypes算法更高,对对象数量较小的Car Evaluation,abalone数据集聚类纯度值较K-Prototypes算法略有下降,但降幅在1%以内。而GDMB K-Prototypes算法处理4个真实数据集运行时间较K-Prototypes算法均有大幅度减少,平均减少了75.19%左右。表明GDMB K-Prototypes算法较K-Prototypes算法在不同数据集上部分聚类效果的下降都在允许范围内,部分数据集效果更好,但整体运行速度有大幅提高、运行时间大幅降低。

论文在人工数据集实验中初步探究了各算法运行结果的聚类纯度、运行时间与对象数量的关系。在人工数据集实验中GDMB K-Prototypes算法与K-Prototypes算法的纯度值相差不大,均在3%以内。而当对象数量逐渐增大时GDMB K-Prototypes算法运行速度较K-Prototypes算法逐渐提升,在对象数量为30000个时,GDMB K-Prototypes算法运行时间是后者的55.61%。表明对象数量越大时GDMB K-Prototypes算法改进迭代计算方式的优势就越能体现出来,聚类速度更快、效率更高。