基于多源数据整合的大学生多级别心理压力智能预测方法

杜文玲

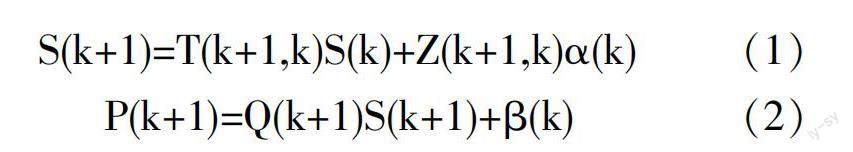
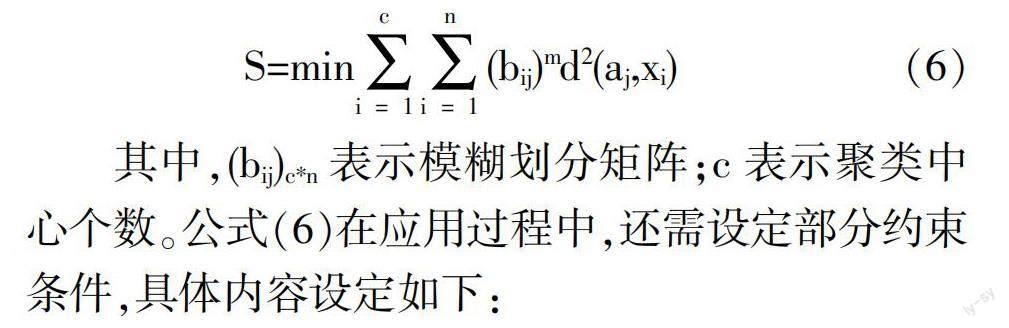
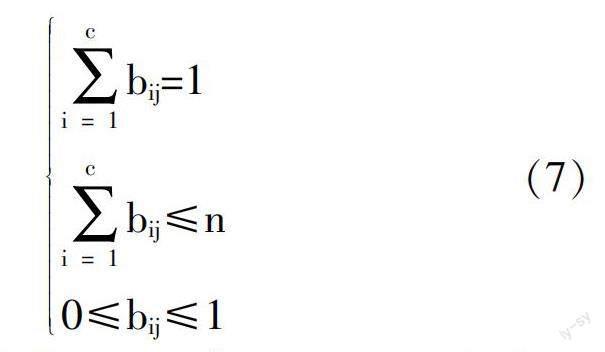
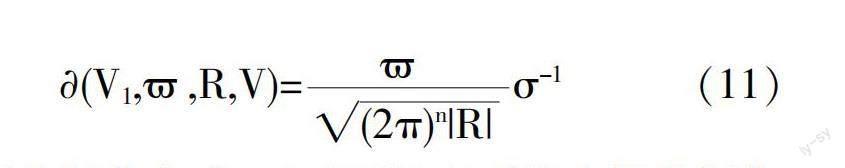
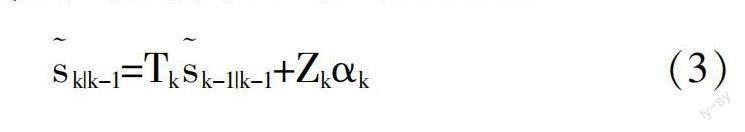
摘 要：针对大学生多级别心理压力智能预测过程中数据的来源较为复杂，导致预测结果可信度较低的问题，提出基于多源数据整合的大学生多级别心理压力智能预测方法。采用卡尔曼滤波法完成数据滤波处理，并应用C均值聚类方法完成数据预处理。使用密度函数计算相关数据结构特征值，引入参数估计算法得到最终可应用于心理压力预测的数据样本，实现数据信息结构整合。计算信息增益率确定数据质量，并应用此数据构建新型大学生多级别心理压力智能预测模型。结果表明，此方法可对数据进行高质量处理，并得到可靠性较高的心理压力预测结果，为大学生心理辅导工作提供帮助。

关键词：Min-Max方法；多源数据整合；心理压力预测；C均值聚类方法；卡尔曼滤波法

中图分类号：TP391；B844.2  文献标识码：A  文章编号：1673-260X（2023）09-0074-04

高校大学生作为未来社会的高层人才，他们是具有高修养以及高素质的群体，同时也是承受较高心理压力的群体[1，2]。由于近年来工作压力与学习压力日益增加，社会对大学生心理承受能力的要求不断提升，大学生心理健康也受到社会各界人士的关注。在对大量在校大学生进行心理分析后发现，20%左右的学生存在不同程度上的心理问题或是心理障碍。大学生的心理障碍问题不仅影响其自身的发展，还会影响社会的和谐性。立足于社会角度，大学生作为国家发展的宝贵人才资源，作为重要的社会发展力量，其心理健康发展需要得到密切的关注。

随着社会的不断发展，教育水平的日益提升，大学生出现了多种不同层级的心理问题，为对其展开更具有针对性的治疗，在过去的研究中部分专家提出了大学生多级别心理压力智能预测方法，但此部分方法在应用的过程中多存在不足，无法为大学生心理辅导提供帮助[3-5]。针对此情况，本次研究中应用多源数据整合技术对采集到的大学生心理素质数据进行整合，并提出更为先进的基于多源数据整合的大学生多级别心理压力智能预测方法，希望此方法可在当前方法的基础上获取可信度更高的心理压力预测结果，为大学生心理疏导提供帮助。

1 大学生心理数据集成预处理

在大学生心理压力预测过程中，需要获取大量的心理测试或行为数据，此部分数据质量与特征选择均对预测模型结果的真实性具有直接影响，决定预测方法预测质量的上限，因此需要对此部分数据进行集成处理。

本次数据处理主要针对异常值与噪声数据进行处理，对于异常值不能采用常规的剔除处理将数据删除，需要首先确定其是否为真异常值。如其为真异常值，再对其进行删除或平均值替换等方法进行处理。异常值处理完成后，对数据中的噪声值进行处理。对比多种数据处理方法后，采用卡尔曼滤波法[6，7]完成数据滤波处理。假设采集到的原始数据为：

其中，S（k）表示k时刻下的数据状态向量；P（k）表示数据观测向量；？琢（k）表示数据处理系统的输入向量；T（k+1，k）表示时刻变动后的数据状态转移矩阵；Z（k+1，k）表示时刻变动后的数据处理系统状态控制矩阵；Q（k+1）表示时刻变动后的预测输出矩阵。此次研究中，将公式（1）视作数据状态方程；公式（2）视作数据测量方程。根据卡尔曼滤波要求，将两公式融合，得到数据中的噪声协方差：

其中，表示数据处理环节状态向量；？琢表示输入向量；Z表示滤波环节控制矩阵；U表示状态转移矩阵；W表示误差协方差矩阵。整合上述公式，得到卡尔曼滤波增益，将此数据带入公式（4）中，得到可应用于心理数据的卡尔曼滤波器，应用此滤波器剔除原始数据中的噪声数据，并设定其他数据处理环节，对其进行后续处理。

由于大学生心理素质数据组成较为复杂且数据来源较多，不同类型、不同性质的数据集成在一起后，为保证数据质量，需对其进行集成整合，以此保证数据质量。对比多种方法后，本次研究采用Min-Max方法[8]对数据进行初步处理，此方法可在一定程度上可有效降低数据规模，减少数据分布差异，提升预测结果的可靠性。根据Min-Max方法的相关要求，将数据初步处理公式设定如下：

其中，a表示采集到的原始数据；max表示此类数据最大值；min表示以此类数据最小值。通过此部分公式，对数据进行初步处理，并将其导入到指定数据库中。而后，使用C均值聚类方法[9]对原始数据进行简单的聚类处理。假设处理后的数据集合为C={c1，c2，…，cn}，此集合为有限数据集合，集合中的数据均为d维向量，将此部分数据整合为模糊划分矩阵形式，并在其中设定聚类中心点，得到数据聚类目标函数：

其中，（bij）c*n表示模糊划分矩阵；c表示聚类中心个数。公式（6）在应用过程中，还需设定部分约束条件，具体内容设定如下：

其中，m表示模糊加权系数；bij表示数据隶属度；aj表示数据集合聚类核心；d表示不同数据核心的距离。在完成数据分类工作后，将数据按照不同类型保存好，为后续的心理健康分析提供数据支持。

2 整合大学生心理数据信息结构

在完成心理压力预测数据的初次数据挖掘后，假设数据库中的多源数据集合为F={Fk|k=1，2，…，m}，数据度量集合为G={Gk|k=1，2，…，m}。在此假设下，数据度量集合可表示多源数据集合的信息结构集合，通过其可确定多源数据集合的内核特征点。本次研究为了更好地完成数据处理工作，使用密度函数计算相关数据结构特征值，引入参数估计算法得到最终可应用于心理壓力预测的数据样本。使用e表示来自不同数据结构集合？字，？酌之前的差异特征。对于数据样本{？酌kl|l=1，2，…}则有：

其中，knl表示第k个信息源的第n个采样点在数据存储空间中的取值结果，在预设条件下，一定存在相应的密度函数，此密度函数可在一定程度上表示不同信息单位的度量值，并由此计算出不同类型源头数据的上近似边界以及下近似边界。

上述计算完成后，使用高低模型导入已经获取到的密度函数，此时高斯函数模型可连续表示为：

其中，V1表示数据存储空间中的矢量；R表示协方差矩阵；？滓表示密度函数均值。针对任意量不同源头数据集合，其密度函数均可应用上述公式计算。根据以上公式，得到多源数据整合密度函数，则有：

应用此部分公式，可对预处理后的全部数据集进行整理，并得到相应的对应的数据结构信息，整理此部分信息，完成大学生多源心理数据的整合工作。

3 构建大学生多级别心理压力智能预测模型

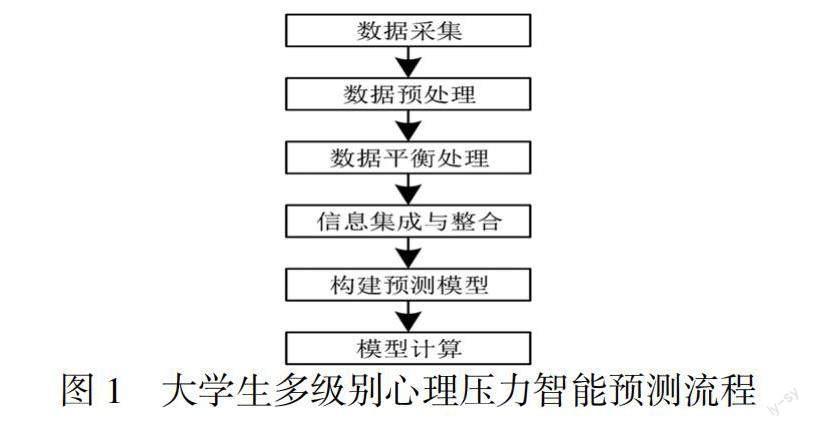
整理上文设定内容，结合以往研究结果，构建大学生多级别心理压力智能预测模型，此模型操作流程具体设定如图1所示。

按照图1设定流程，本次研究将决策树划分为系统树、主树以及子树，通过三层决策树对大学生心理数据进行预测，并得到最终的大学生多级别心理压力预测。整理上述内容，将其有序连接，至此，基于多源数据整合的大学生多级别心理压力智能预测方法设计完成。

4 实验论证分析

4.1 实验准备

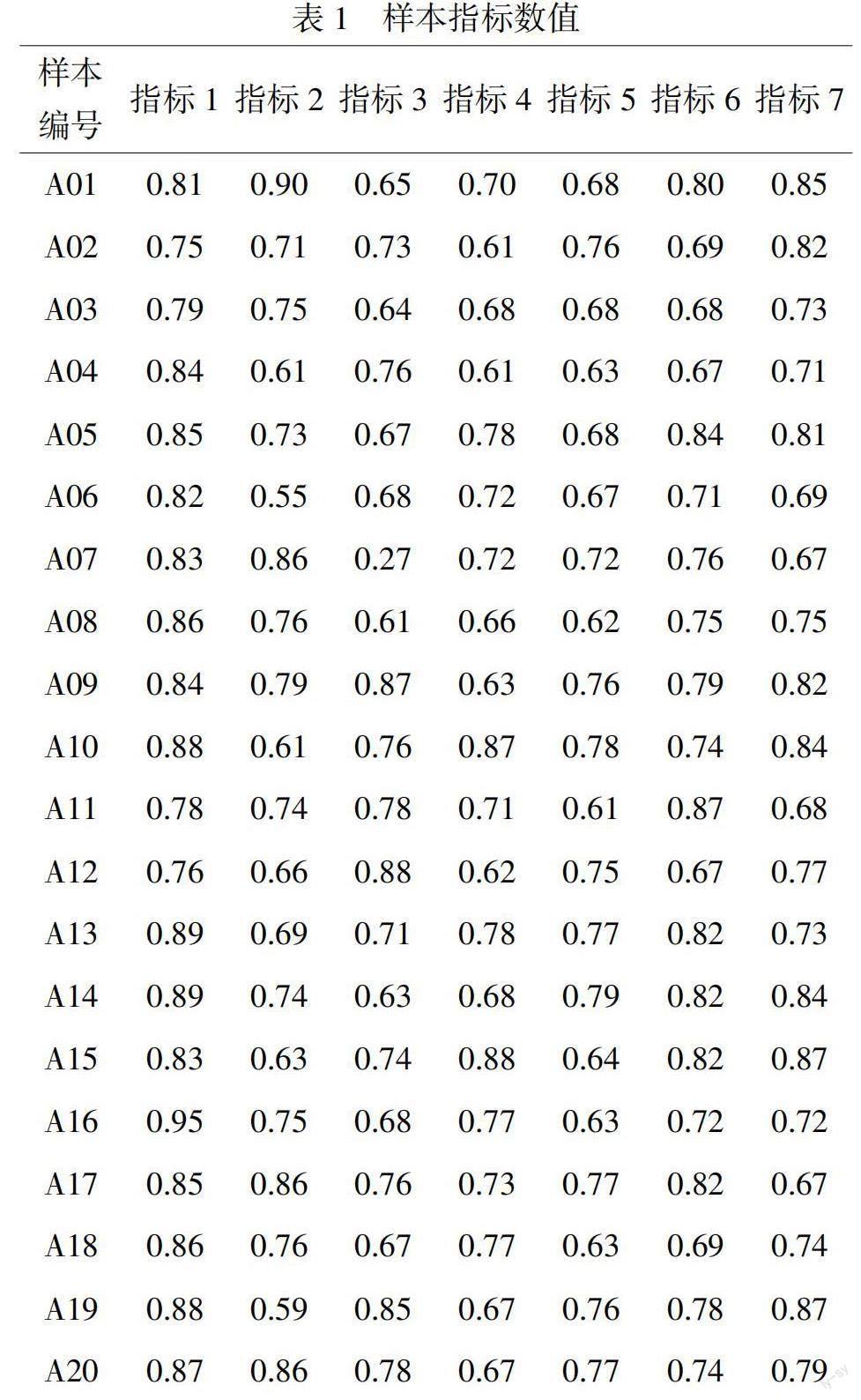
本次实验在对大量心理测试案例进行分析后续，将本次研究中需要采集的大学生心理多级别压力预测数据划分为个人智力、情绪健康、意志健全、人格完整、自我评价正确、人力管理良好、社会关系正常7个方面。为保证本次实验具有较为可信的实验结果，选择某高校的部分学生作为实验志愿者，获取20位学生的原始心理健康指数，构建原始数据集，具体内容如表1所示。

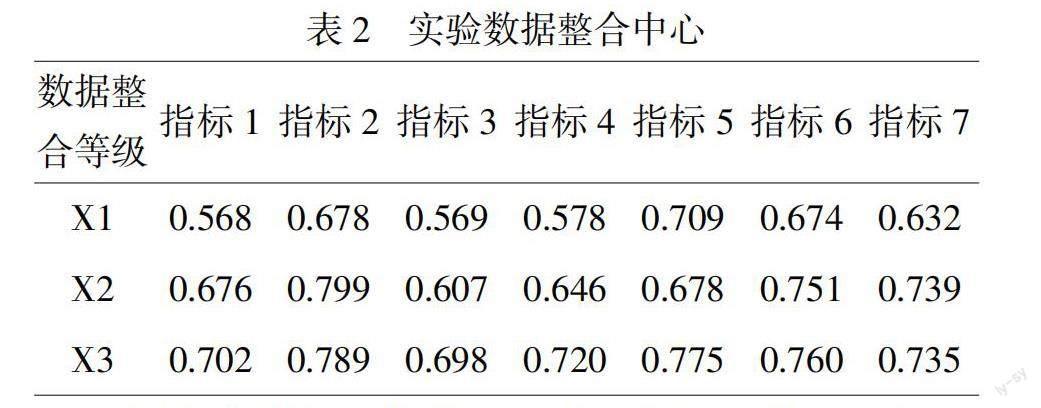
对表1中数据进行多次迭代运算，得到以上7种指标的数据整合中心，如表2所示。

综合分析上述数据后，将原始样本的心理压力划分为3个层级，具体层级划分结果如下：

I级：A05、A06、A07、A11、A12、A15、A20

Ⅱ级：A03、A04、A08、A010、A16、A17、A18、A01、A02

III级：A09、A13、A14、A19

将上述数据作为此次实验的数据基础，并使用文中方法、基础方法以及人工智能方法对实验样本心理压力进行等级预测，确定不同方法的预测能力与应用效果。

4.2 数据整合精度实验结果分析

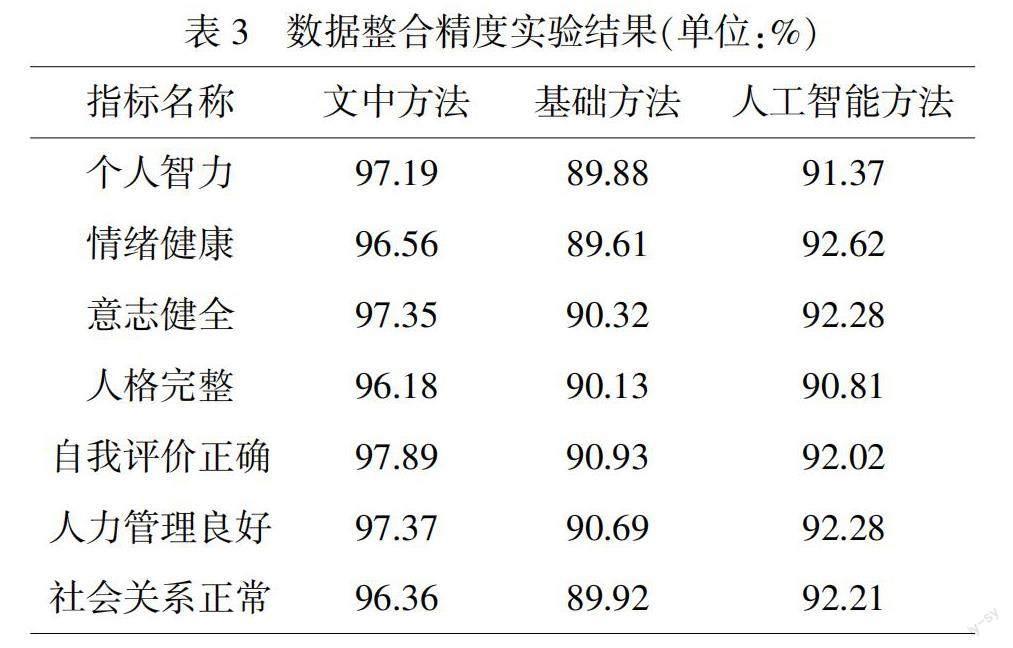
使用不同方法对获取到的原始数据进行整理，并分析不同方法应用，不同指标整合精准度，具体实验结果如表3所示。

分析表3中数据可以看出三种方法使用后，所得数据整合结果具有较大的差异。文中方法使用后，各个指标数据的整合精度得到明显的提升，此方法整合后的数据整体质量较高。基础方法可对部分数据进行高质量整合，无法对整体数据进行整合，使用此部分数据所得预测结果可靠性较差。人工智能技术在一定程度上缓解了基础方法的不足，但其应用效果无法与文中方法相比，因此在日后的研究中还需对其进行优化，以此提升此方法的数据处理能力。

4.3 大学生心理多层级压力预测准确性实验结果分析

应用不用方法的预测过程，所得预测结果如下所示：

文中方法预测结果：

I级：A05、A06、A07、A11、A12、A15、A20

Ⅱ级：A03、A04、A08、A010、A16、A17、A18、A01

III级：A09、A13、A14、A19、A02

基础方法：

I级：A05、A06、A07、A11、A12、A15、A20

Ⅱ级：A08、A010、A16、A17、A18、A02

III级：A09、A13、A14、A19、A03、A04、A01

人工智能方法：

I级：A05、A06、A07、A11、A12、A15、A20

Ⅱ级：A03、A04、A08、A010、A16、A17、A18、A01、A02、A14、A19

III级：A09、A13

分析上述内容可以看出，三种方法的预测结果与预设的心理压力分级结果存在不同，但文中方法对预设方法较为接近。为了更好地对上述结果进行分析，使用以下公式确定不同方法的预测准确率：

其中，i表示正确预测结果；？灼all表示全部预测结果。应用此公式可以发现，文中方法的预测准确率为97.50%；基础方法的预测准确率为89.0%；人工智能方法的预测准确率为92.3%。由此部分数据可以确定，文中方法的预测结果具有较高的可信度。综合上述实验结果可知，文中方法的应用效果优于其他两种方法，其具有较高的数据处理能力。

5 结束语

针对大学生多级别心理压力预测过程中，数据量较大、类别较为复杂，且预测方法数据处理能力不佳，导致预测结果可靠性较差的问题，提出应用多源数据整合技术的新型预测方法。此方法经实验证实，其应用效果优于当前可应用预测方法。但本次研究数据样本较少，所得结果不具备普遍性，在日后的研究中还需增加数据样本，对此方法进行大规模测定，以保证其符合当前心理测试要求。

——————————

参考文献：

〔1〕王样，胡雨含，周楚雯，等.基于KANO模型和PCSI指數的大学生心理健康服务设计研究[J].包装工程，2023，44（06）：84-93.

〔2〕徐伟华，黄旭东，蔡可.基于粒计算的多源信息融合方法综述[J].数据采集与处理，2023，38（02）：245-261.

〔3〕林艳飞，龙媛，张航，等.基于XGBoost的多种生理信号评估心理压力等级方法[J].北京理工大学学报，2022，42（08）：871-880.

〔4〕家晓余，张宇驰，邱江.思维模式对大学生情绪健康的影响：压力知觉和心理韧性的链式中介效应[J].西南大学学报（社会科学版），2022，48（04）：202-209.

〔5〕朱逢乐，严霜，孙霖，等.基于深度学习多源数据融合的生菜表型参数估算方法[J].农业工程学报，2022，38（09）：195-204.

〔6〕张书钦，白光耀，李红，等.多源数据融合的物联网安全知识推理方法[J].计算机研究与发展，2022， 59（12）：2735-2749.

〔7〕王东方，孙梦，欧阳萱，等.简版社区心理体验评估测评大学生的效度和信度[J].中国心理卫生杂志，2022，36（02）：172-178.

〔8〕黄伍，龙文浩，刘铸，等.多维度智能心理测评系统[J].计算机应用，2021，41（S2）：192-197.

〔9〕王姝，任玉，关展旭，等.基于差异信息量的多源数据融合方法[J].东北大学学报（自然科学版），2021， 42（09）：1246-1253.