基于小波分析的小电流接地系统单相接地故障选线的研究

国网宜昌供电公司 周轩锋

综合当前研究现状来看，在小电流接地系统的发展中，单相接地配电网故障选线自动化技术得到了广泛应用，虽然一些专家学者对此展开了深入的探讨与分析，但是总的来说，当前并未研发出更加安全可靠、适用于各种紧急情况的故障选线技术解决方法。所以，为了适应时代的发展趋势，对于高性能的配电网故障选线自动化技术也提出了更高要求。小波变换本身具有较强的对小电流暂态信号进行分析和处理的数据分析能力，能够准确提取其中的暂态分量和信号在线路中的实际应用信息，为小电流故障处理和选线的实现提供了支持。本文主要研究小波变换在小电流单相接地系统故障处理和选线过程中的实际应用。

1 小电流接地系统单相接地故障分析

1.1 小电流单相接地故障的稳态特征分析

我国电力系统的中性点经常采用不接地、经消弧线圈接地两种方式，因此本文主要介绍这两种接地方式。

1.1.1 中性点不接地系统单相接地故障分析

假设系统模型为三条出线的无限电源，三条出线具有不同的长度，在L1线的C相中，产生了单相金属接地故障的问题。单相接地故障电容电流在进行分析时，所提出的假设包括[1]：系统在运行过程中，所选用的即为三相对称系统的形式，三相相称是电压对称；每条线路三相对地电容相等，并且采用集中电容的方法，对分布式电容进行替代；对各条线路所产生的三相对地电导予以忽略。

根据非故障线路L2可以得出，因为C相电压表示为0，其相对电容电流也表示为0，随着相电压的加大，A相与B相对地电容电流也hi随之增加。与之相对应的对地电容基波电流的计算公式具体如下：，如上述公式所示，在线路L2中，A、B、C这三相所对应的对地电容几波电流，分别表示的是。当A相与B相法神故障之后，所产生的对地电压分别对应的是。电网角频率则可表示为w。C02表示的即为各相产生的对地电容。

通过对非故障线路L2进行研究后发现，基波零序电流的计算公式如下所示：，公式中，中性点的位移电压表示为，与发生故障之前的相电压是相同的。其中，关于基波零序线路电流流动方向的变化，则是从母线直流到其他线路，大小为线路L2三相对地电容电流的相量和。同理，对于非正常故障的该母线L3而言，流动方向则是从母线路直流到其他线路，大小大约为L3三相对地电容电流的相量和。

对于全部分系统的各条故障电源线路以及L1而言，其和非系统故障电源线路以及L2、L3的根本功能区别主要地方在于：故障点流回非故障相的对地电容电流。三个相对地电容的基波电流分别为：、、，此时故障线路L1的基波零序电流为：。

总的来说，在该系统中，单相金属性接地系统故障的特点可以总结为以下几项：在发生故障之后，所产生的非故障相对地的电压则可表示为0，电压升高为线路故障前的电压或线路相对地电压，相当于发生故障之前的倍；供电系统三相线路负荷的电压仍然对称，不过会影响对负荷的供电；控制系统两个中性点的直流电压由正常电路故障前的0V点电压逐渐变化为正常电路故障前的相对点电压；在非故障线路中，关于基波零序电流方向，则是从母线流向线路，幅值为三条相对接地线零序相电流的相量和；在故障线路中，关于基波零序相电流由路流向母线，所产生的幅值则可表示为非故障线路形成的零序电流得出的相量和。

1.1.2 中性点经消弧线圈接地系统单相接地故障分析提出一个假设，系统模型等同于中性点不接地系统的模型，二者的区别体现在线路上的中性点经过消弧之后，可以实现线圈接地。为了方便地对比及准确分析引起问题的原因使其简单化，仍然可以提出这一假设，在系统线路L1中，中性点与相线圈之间出现了故障问题，也就是单相线圈金属性接地的故障现象。相比于中性点不接地来说，非接地故障线路的许多方面均与之相同，包括对地电容电流与基波零序电流等方面的分布状况[2]。非故障线路的零序电流方向、大小与非故障线路的基波零序电流一样。综上所述，该类故障所具有的特征可总结为以下几点：在发生故障之后，后线路所产生的电压相对地面表示为0，和线路的电压相对地增加的电压故障前的线或线相对地电压，这是时代的相对地电压增加之前的倍；供电系统三相线路负荷的电压仍然对称，不过会影响对负荷的供电；系统的中性电压由0V变为故障之前的相电压。

1.2 小电流接地系统单相接地故障的暂态特征分析

通过对中性点经消弧线圈接地系统进行研究后发现，当出现金属性接地故障问题的情况下，对系统的暂态电流进行分析时，具体方法如图1所示[3]。

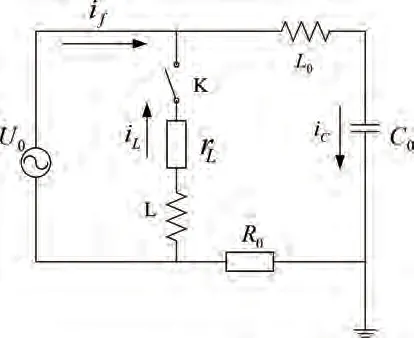
图1 暂态过程的等效电路

根据图1可得出，零序回路的电源表示为U0；消弧线圈产生的有功损耗电阻则可表示为rL：L表示消弧线的电感分量；电网所具有的三相对地电容可以表示为C；L0为零序电路中电源与电路的等效电感；在零序电路中，电阻的和表示为R0。为了方便进行分析与研究，提出一个假设，系统在运行时出现了金属性接地故障的问题。在得出各元件参数后，利用该模型展开深入地分析，将会得出更加精准的结果。受到其他因素的影响，经过分析后得出，暂态接地电流是最大的，同时也具有最为严重的问题。微分方程组具体如下所述：

在上述公式中，流过电容产生的暂态电容电流可以表示为ic，iL为流过电感的暂态电感电流，Um为零序电源的电压幅值，所得出的结果与故障前相电压的幅值是相同的。

根据上述公式，则可得出以下几项参数的计算结果，包括暂态电容电流ic暂态电感电流iL以及暂态接地电流id，具体如下所示：、、，式中：ICm和ILm分别为瞬态电容电流幅值和瞬态感应电流幅值式中，其中ICm=UmωC，ILm=Um/（ωL）；δ表示的是自由振荡分量所产生的衰减因子，在电容回路中，产生的时间常数表示为rc；在电感回路中，这一时间常数表示为rL：角频率；其中的为回路的自振角频率。

2 两种接地方式的仿真模型

在以下仿真模型中，是基于10kV小电流单相接地故障系统产生的。其中系统频率为50Hz，仿真时间为0～0.1s，其他参数见表1。

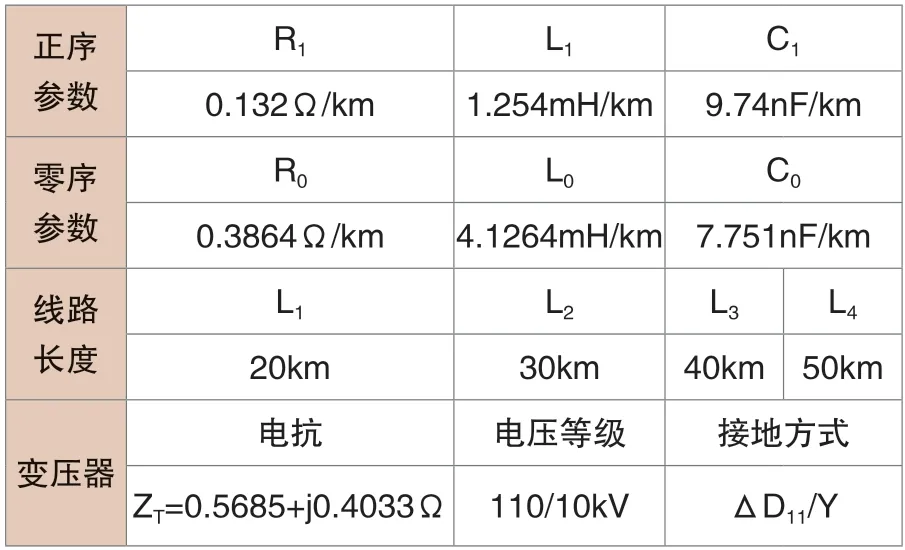
表1 参数表

2.1 中性点不接地系统故障选线仿真

系统正常时的三相电压和三相电流的幅值稳定，相位角也相同。接下来我们假设某条线路故障，再来用MARLAB进行仿真。在Simulink中于时间0.01s设置一个故障，故障离母线距离为3km，在0.08s时移除故障，可以获得其过程中电流、电压。

根据图2和图3的波形可以看到，在0.001s后故障点被植入，A相电流的幅值明显变大，电压却变为了零。而B、C相的电压幅值也有所改变，变为原来的倍。在0.08s故障点被移除，三相电压电流恢复又正常。这也与上文的结论相符合。在相同的状态下，能够得出不同线路的各项波形图。

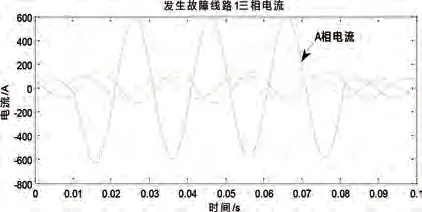
图2 线路1的三相电流

图3 线路1故障点三相电压

可以从图4中看到，通过对线路1的波形进行研究后发现，与其他三条线路具有相反的波形方向，相比之下也具有更大的幅值。从图5中可以得知，线路无故障时零序电压为0。这样就可以通过比较知道线路1为故障线路。

图4 线路1发生单相接地故障时各线路的零序电流

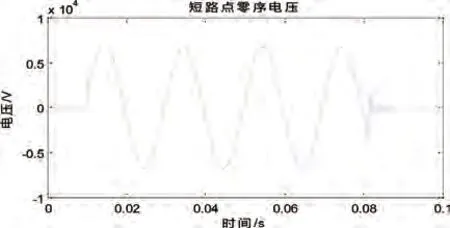
图5 故障后零序电压

2.2 中性点经消弧线圈接地系统故障选线仿真

使系统在运动过程中，采用中性点经消弧线圈接地的方式，同样用Simulink在时间为0.01s时设置一个故障，故障离母线距离为3km，在0.08s时移除故障，可以得到四条线路的零序电流、零序电压的波形图。

根据图6，与中性点不接地方式相同，可以看出线路1波形的方向与线路2、3、4是相反的。但是也能看出零序电流的幅值变小了。再比较零序电压，基本没有变化。

图6 经消弧线圈接地系统故障时零序电流和零序电压