基于参数自寻优变分模态分解的信号降噪方法
何成兵, 车其祥, 徐振华, 于庆彬, 董玉亮, 程睿翔
(1.华北电力大学 能源动力与机械工程学院,北京 102206;2.国网福建省电力公司电力科学研究院,福州 350007;3.国网山东省电力公司电力科学研究院,济南 250000)
滚动轴承在各类旋转机械设备中应用广泛,同时也是设备中最易损坏部件之一。统计数据表明,在使用滚动轴承的旋转机械中,约30%的机械故障是由滚动轴承引起的。滚动轴承振动信号具有冲击性、非线性、非平稳的特性,信号微弱、调制性强,而且由于旋转机械设备运行工况复杂,背景噪声污染严重,导致滚动轴承故障信号常常淹没于噪声之中[1]。因此,对滚动轴承故障信号进行降噪处理,获得有效故障特征,对于后续的故障信号分析与故障诊断具有重要的意义。
目前常用的降噪方法有小波变换(wavelet transform, WT)、经验模态分解(empirical mode decomposition, EMD)、集合经验模态分解(ensemble empirical mode decomposition, EEMD)以及变分模态分解(variational mode decomposition, VMD)等。WT在信号降噪处理时的缺点是小波基函数和小波阈值函数的选择不具有唯一性,受主观性影响较大,很难保证降噪效果最优。为克服WT的缺点,曹玲玲等[2]结合快速谱峭度和带通滤波以及Hilbert包络分析,提出了一种新的改进小波阈值函数进行信号降噪;Malla等[3]利用复Morlet小波分析,得到滚动轴承故障的相位图和振幅图,有效提取出了轴承故障特征。
EMD方法在信号分解过程中存在模态混叠、端点效应及产生虚假分量等缺陷,使得信号中特征频率与噪声的分离程度不足[4]。EEMD对EMD进行了优化改进,李思琦等[5]利用EEMD对信号进行分解,提出了一种基于EEMD与卷积神经网络相结合的滚动轴承故障诊断方法;Yin等[6]利用改进EEMD将原始信号中隐藏的固有噪声分离,提出了一种基于改进EEMD和自适应阈值去噪的滚动轴承弱故障特征提取新方法。EEMD可以在一定程度上抑制模态混叠现象,但也存在计算量大、频谱剖分效果不理想的缺点。
VMD是一种新的非递归信号分解方法,它克服了EMD等算法存在的模态混叠和频率效应等缺点,具有很好的噪声鲁棒性和降噪效果,得到了广泛应有。Wang等[7]采用VMD进行碰摩信号的等效滤波特性分析,并与EWT、EMD和EEMD方法进行了比较,证明VMD在提取瞬态冲击方面更有效;朵慕社等[8-10]提出一种基于改进VMD降噪和卷积神经网络的轴承故障智能诊断方法,其VMD分解层数通过排列熵阈值法确定,结合峭度准则和互相关准则,进行IMF分量选取与信号重构,取得了较为理想的降噪效果。
在利用VMD进行信号降噪处理时,需提前设定模态数K和二次惩罚因子α等参数,由于K和α的取值对降噪效果有很大的影响,它需要自适应获得最佳值,而不是人为主观设定。目前主要采用以下三种途径来获得K和α的优化参数[11]:一是根据先验知识或中心频率观察法选取,如Qiao等[12]对原始信号进行VMD分解时,根据每个IMF分量的中心频率确定K值,这种方法适应性较差,且不能保证VMD分解精度;二是通过评价指标来选取,如Zhang等[13]通过能量和相关系数确定K值,这种方法选取的K值并不适用于所有的信号;三是采用元启发式算法进行参数自适应寻优,如人工鱼群算法(artificial fish swarm, AFS)[14]、灰狼算法(grey wolf, GW)[15]、蚱蜢算法(grasshopper optimization, GO)[16]、鲸鱼算法(whale optimization, WO)[17]、蝙蝠算法(bat optimization, BO)[18]和粒子群算法(particle swarm optimization, PSO)[19]等,这些优化算法可搜寻到优化参数,但一般需要大量的迭代计算,同时,由于各实际应有领域的信号与噪声特点不同,这些算法在应用于具体领域时,如何设定恰当的适应度函数、如何提高算法搜索能力以及避免陷入局部最优解,是急需解决的问题。
针对上述问题,本文提出了一种基于参数自寻优变分模态分解的信号降噪方法。首先提出了一种改进粒子群算法(improved particle swarm optimization, IPSO),以实现VMD最优模态数K和二次惩罚因子α的自适应寻优,该算法结合滚动轴承故障信号特点,建立了模态复合熵新指标,并以之作为适应度函数,同时设计了惯性权重值随搜索进程先大后小的计算公式、边界粒子以及粒子群优化处理原则,既提高了IPSO算法搜索能力,又避免了算法早熟收敛、陷入局部最优解;然后基于最优K和α,对原始信号进行VMD分解,获得K个IMF分量;利用相关系数筛选法,进行IMF分量的有效模态和含噪模态识别,并利用小波阈值去噪方法对含噪模态进行去噪处理;最后将有效模态与去噪后的含噪模态进行重构,实现信号降噪。数值仿真和试验数据分析表明本文所提方法降噪效果明显,有利于滚动轴承故障特征的提取。
1 相关理论基础
1.1 VMD算法
VMD将一个时域信号f(t)分解为K个具有调频-调幅特性和稀疏特性的本征模态函数uk(t)
uk(t)=Ak(t)cos(φk(t))
(1)
各IMF中心频率为ωk(t),为使每个模态的估计带宽之和最小,建立如下约束变分模型
(2)
为求取式(2)最优解,引入扩展Lagrange函数,将约束性变分问题变换为非约束性变分问题,其表达式为
(3)
式中,α为二次惩罚因子,用于保证信号的重构精度,α值越大,各模态分量的频率带宽就越小。
利用交替方向乘子算法求取式(3)的鞍点,即求取约束变分模型的最优解,其中模态分量uk及中心频率ωk分别为
(4)
(5)
VMD算法实现过程如下:
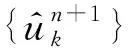
(6)
步骤4 重复步骤2、步骤3,直到满足式(7)所示的迭代停止条件,结束循环,得到K个变分模态分量。
(7)
式中,ε为求解精度。
1.2 PSO算法
PSO算法模拟鸟群的捕食行为,将每只鸟视为粒子,作为基本运算单位,其优化问题的实质是通过粒子的运动方向和速度确定最优解在空间中的位置。其基本原理为:设搜索域为D维,共有m个粒子构成群体,第i个粒子位置表示为向量xi=(xi1,xi2,…,xiD),飞行速度表示为向量vi=(vi1,vi2,…,viD),xi位置变化就是解的轨迹,用适应度函数Q(xi)来权衡粒子位置的好坏。第i个粒子所经历的个体最优位置记为pi=(pi1,pi2,…,piD) ,搜索域中整个粒子群全局最优位置记为pg=(pg1,pg2,…,pgD)。各粒子的速度和位置通过下式更新
vid(k+1)=ωvid(k)+c1r1(pid(k)-xid(k))+
c2r2(pgd(k)-xid(k))
(8)
xid(k+1)=xid(k)+vid(k+1)
(9)
式中:k为粒子群迭代次数;i=[1,m]为粒子数;d=[1,D]为空间维数;r1和r2为相互独立的0~1之间的随机数;c1和c2分别为粒子向个体和全局最优位置方向的学习因子;vid(k)和xid(k)分别为第i个粒子在d维空间内k次迭代的速度和位置;pid(k)和pgd(k)分别为第i个粒子在d维空间内k次迭代的个体和全局最优位置;ω为惯性权重。
PSO算法实现过程如下:
步骤1 算法初始化,设定粒子群的维度D、群体规模m、最大迭代次数Np、粒子位置范围、速度范围。
步骤2 计算每个粒子的适应度函数值,确定粒子个体最优位置pi=(pi1,pi2,…,piD)和粒子群全局最优位置pg=(pg1,pg2,…,pgD)。
步骤3 根据式(8)、式(9)更新调整粒子的速度和位置。
步骤4 迭代终止条件一般选为最大迭代次数Np或粒子群最优位置小于设定的最小阈值,判断是否满足迭代终止条件,不满足则转到步骤2,满足则结束。
1.3 小波阈值去噪算法
小波阈值去噪是建立在小波变换基础上的算法,其基本原理为:对含噪信号进行小波变换,根据信号具有真实信号通常为低频、噪声信号多为高频的特点,对各频带小波系数与小波阈值进行比较,甄别出有效信号与噪声信号,并通过小波重构得到去噪信号。
小波阈值去噪算法实现过程如下:
步骤1 设定小波分解层数,选定小波基函数,构造小波阈值函数。
步骤2 使用选定的小波基函数对含噪信号进行Mallat算法处理,得到分解层数对应的小波高频系数和低频系数;
步骤3 将小波系数与小波阈值进行比较,如果小波系数大于小波阈值,对应数据为有效信号,则该小波系数保留;反之,为噪声信号,该小波系数舍弃。
步骤4 对保留的小波系数重构,得到去噪信号。
2 改进粒子群算法(IPSO)
本文提出了一种改进粒子群算法(improved particle swarm optimization,IPSO)进行VMD参数自适应寻优,以确定VMD最优的K和α。该算法的特点在于:从滚动轴承故障信号特点出发,提出了模态复合熵新指标,并以之作为适应度函数;设计了惯性权重值随搜索进程先大后小的计算公式、边界粒子以及粒子群优化处理原则,提高了IPSO算法搜索能力,也避免了算法早熟收敛、陷入局部最优解。
IPSO算法流程如图1所示,具体实现过程如下:
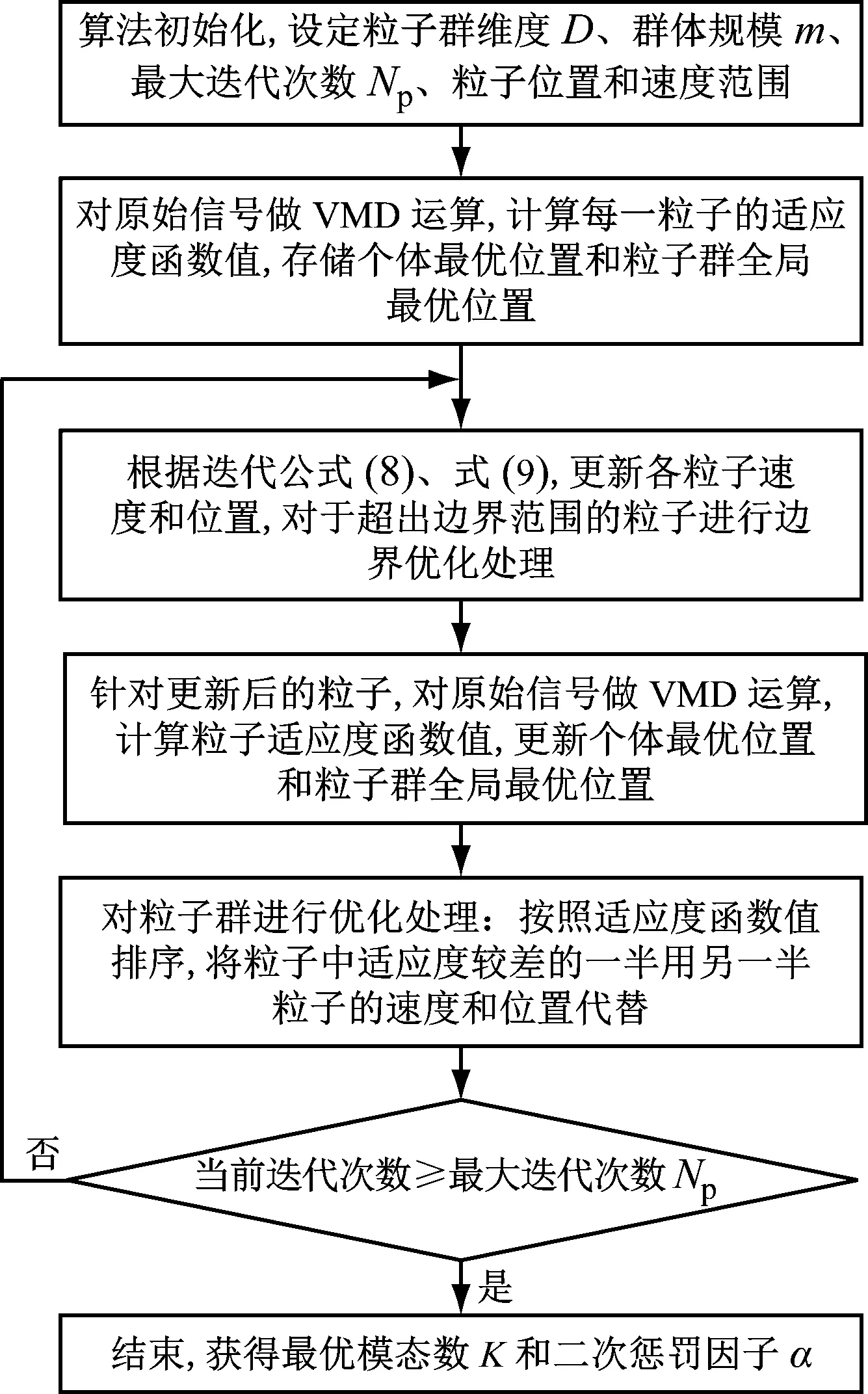
图1 IPSO流程图Fig.1 The flow diagram of IPSO
步骤1 算法初始化。设定粒子群维度数D为 2,对应VMD的模态数K和二次惩罚因子α;在2维可行域中随机选取m个粒子,对粒子位置、飞行速度随机初始化;第i个粒子在2维空间的位置表示为向量xi=(xi1,xi2),飞行速度表示为向量vi=(vi1,vi2)。
步骤2 针对某一粒子的2维位置组合,对原始信号做VMD运算,得到K个模态分量{uk},计算每一粒子的适应度函数值Q(uki(1)),对各粒子进行评价,选取适应度函数值最小者为最优,存储对应粒子的个体最优位置pi=(pi1,pi2) 以及整个粒子群全局最优位置pg=(pg1,pg2)。
通过对{uk}分析发现:如果{uk}中包含噪声越多,则信号复杂性越高,对应的模态复合熵越大,反之,则模态复合熵越小。因此,以{uk}的模态复合熵Ec作为适应度函数Q(uk),且以模态复合熵最小作为适应值,适应度函数如式(10)所示
Q(uk)=Ec=β1·Eenergy+β2·Eenvelope
(10)
式中:Eenergy为模态能量熵;Eenvelope为模态包络熵;β1,β2为二者的权重系数,β1+β2=1,对于如滚动轴承故障这样具有明显冲击特征的信号,取β1<β2,否则取β1≥β2。
模态能量熵Eenergy的计算式如下
(11)
模态包络熵Eenvelope的计算式如下
(12)
式中,H为信号uk的Hilbert变换。
步骤3 根据迭代公式(8)更新各粒子速度,根据式(9)更新各粒子位置。
式(8)中惯性权重ω对算法搜索结果影响较大,其取值大则种群粒子搜索能力强,可探索较大的区域,取值小则可精细搜索目标,局部搜索能力强。为提高算法搜索能力,同时避免陷入局部最优解,采用ω权重值随搜索进程先大后小的原则动态设定
(13)
式中:ωmax,ωmin为惯性权重的最大值和最小值,取ωmax=0.9,ωmin=0.4;t为粒子迭代次数;Np为最大迭代次数;Dec为衰减因子,其值为小于1的正数。
粒子位置更新后,有可能出现粒子的某一维度超出设定范围的情况,此时粒子容易在边界附近聚集,导致算法早熟收敛。因此,对超出边界范围的粒子进行边界优化处理:将该维度的位置值设置为边界值;该维度的速度乘以0~1之间的随机数,并将其方向设为反方向,以此缓解因粒子在边界聚集而引起的算法早熟收敛。计算公式如下
(14)
式中:xid,vid是第i个粒子第d维的位置和速度;xmaxd,xmind是粒子第d维的上限和下限值。
步骤4 针对位置更新后的粒子,对原始信号做VMD运算,计算每一粒子新的适应度函数值Q(uki(k+1)),并更新粒子个体最优位置pi(k+1)及粒子群全局最优位置pg(k+1)。粒子i的个体最优位置更新公式如下
pi(k+1)=
(15)
粒子群全局最优位置更新公式如下
(16)
步骤5 为提升算法性能,提高算法收敛速度,对粒子群进行优化处理:按照适应度函数值对所有粒子进行排序,并将粒子中适应度较差的一半用另一半粒子的速度和位置代替,但不改变原有粒子的个体最优位置pi(k+1)和粒子群全局最优位置pg(k+1)。
步骤6 判断当前迭代次数是否达到最大迭代次数Np,如果未达到,返回步骤3进行下一次迭代;如果已达到,则迭代终止,输出最优粒子2维位置,即获得最优模态数K和二次惩罚因子α。
3 本文所提降噪方法流程
本文提出的基于参数自寻优变分模态分解与小波阈值处理的信号降噪方法流程如图2所示,具体实现步骤为:
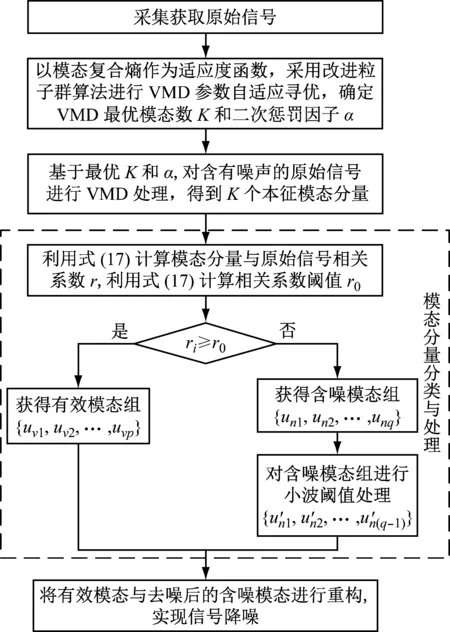
图2 本文降噪方法流程图Fig.2 The flow diagram of signal denoising method in this paper
步骤1:采集获取原始信号x(t);
步骤2:以模态复合熵作为适应度函数,采用IPSO算法进行VMD参数自适应寻优,确定VMD最优模态数K和二次惩罚因子α;
步骤3:基于最优模态数K和二次惩罚因子α,对含有噪声的原始信号进行VMD处理,得到K个本征模态分量{uk};
步骤4:利用相关系数筛选法,进行模态分量{uk}的有效模态和含噪模态分类,利用小波阈值去噪方法对含噪模态进行去噪处理。具体流程如下:
(1) 利用式(17)计算各模态分量{uk}与原始信号x(t)之间的相关系数r,相关系数越大,表示两信号之间的关联性越强
(17)
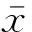
利用下式计算相关系数阈值r0
(18)
式中,rmax为各模态分量相关系数最大值。
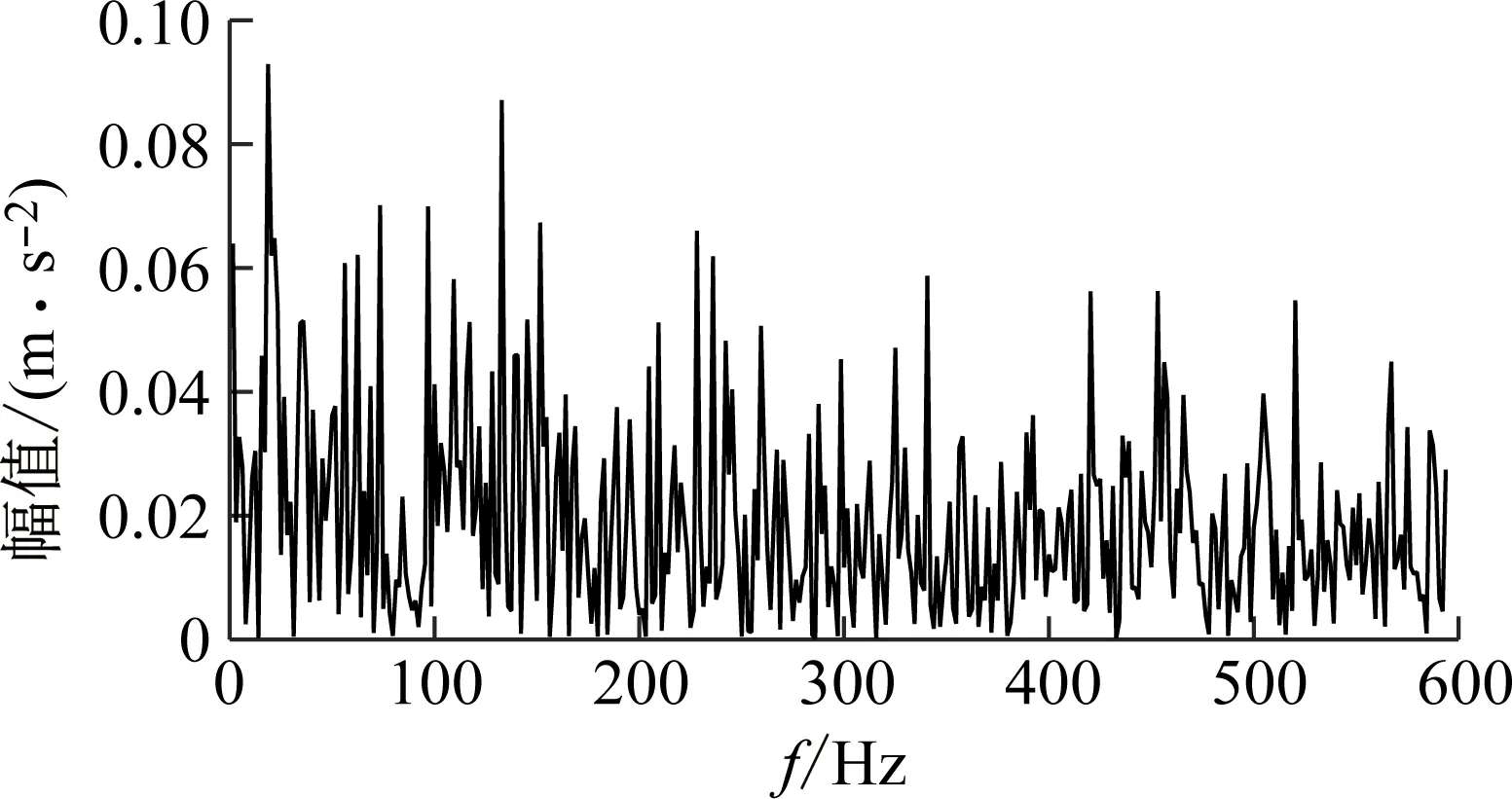
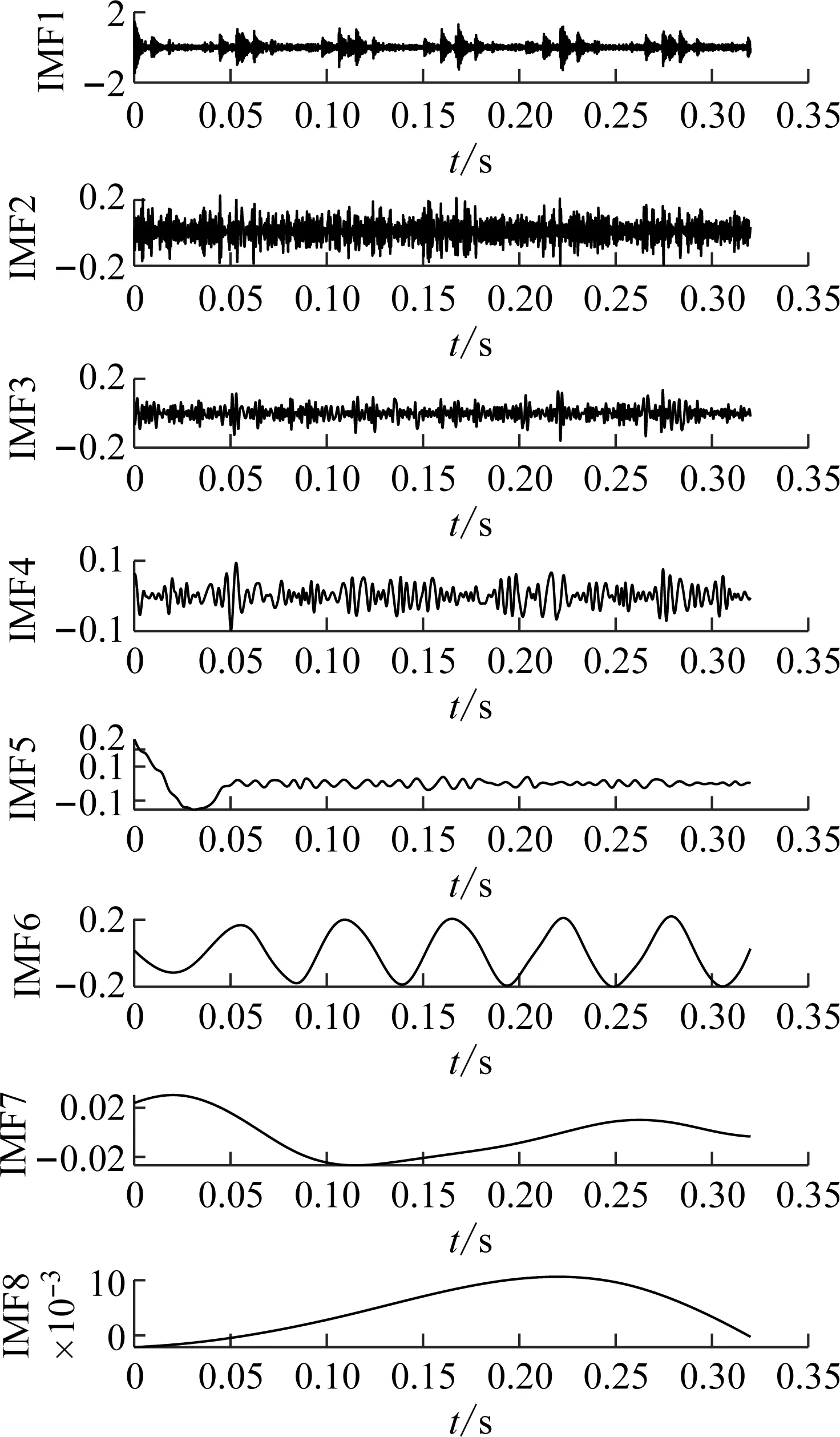
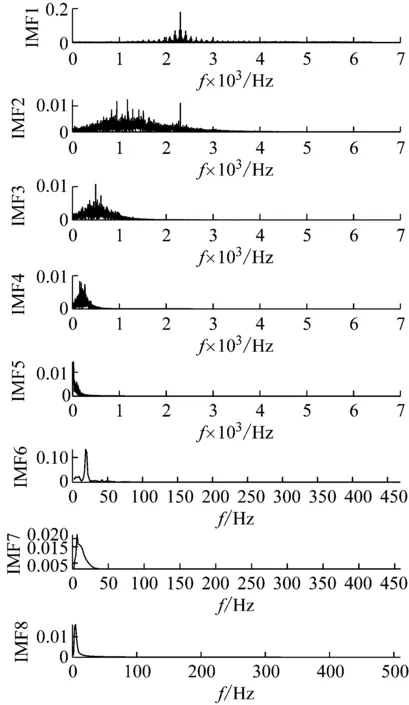
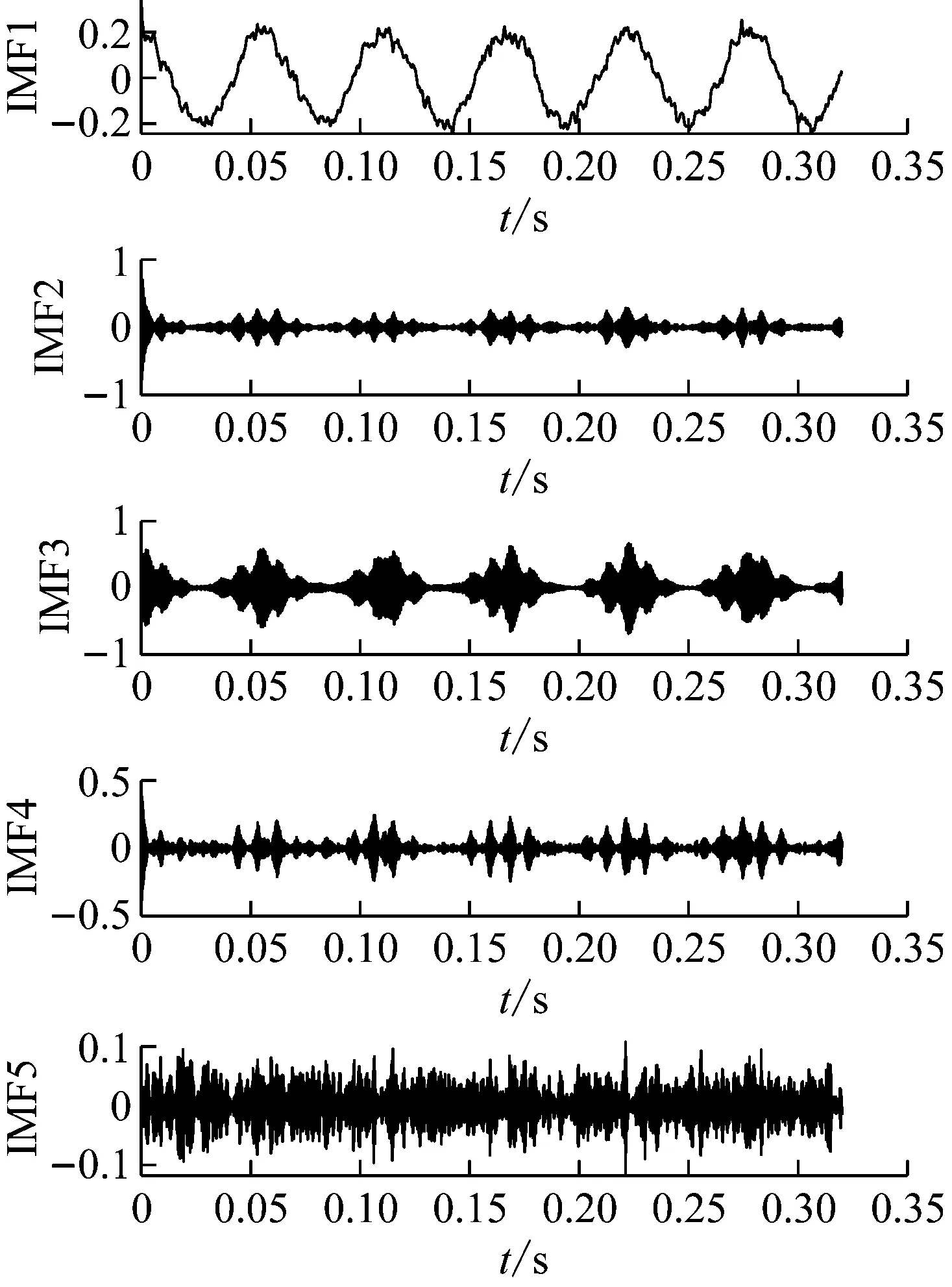
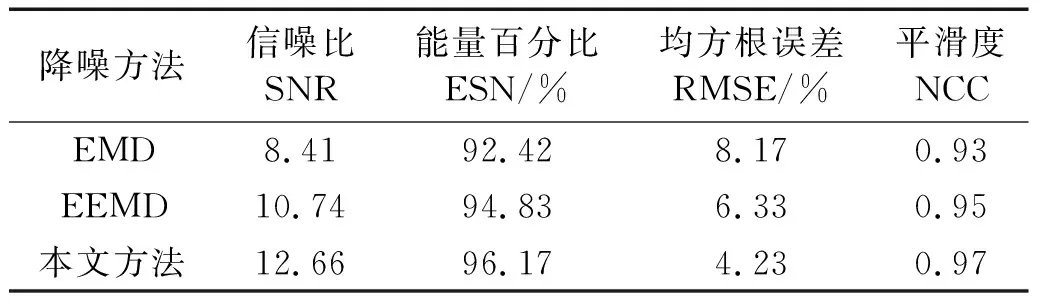
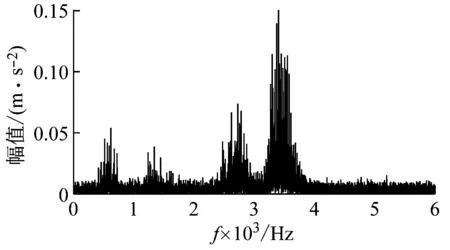
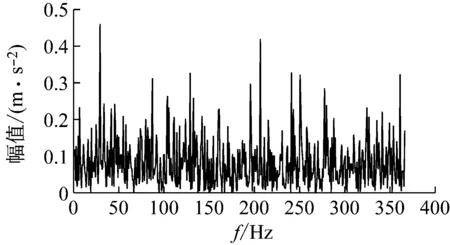
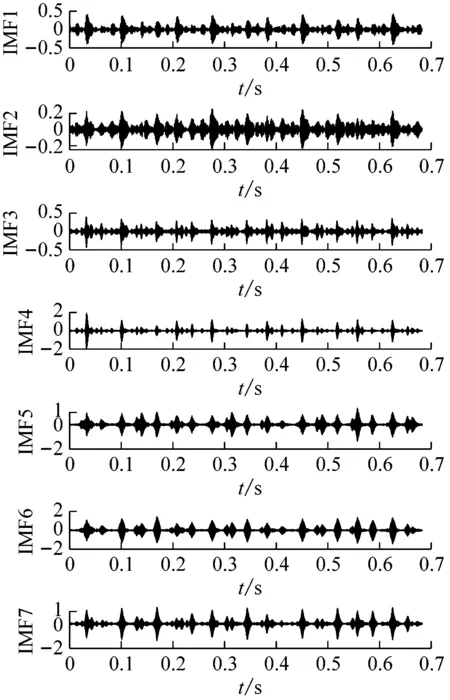
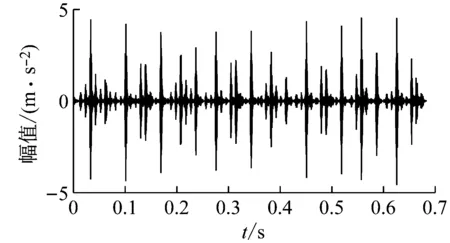
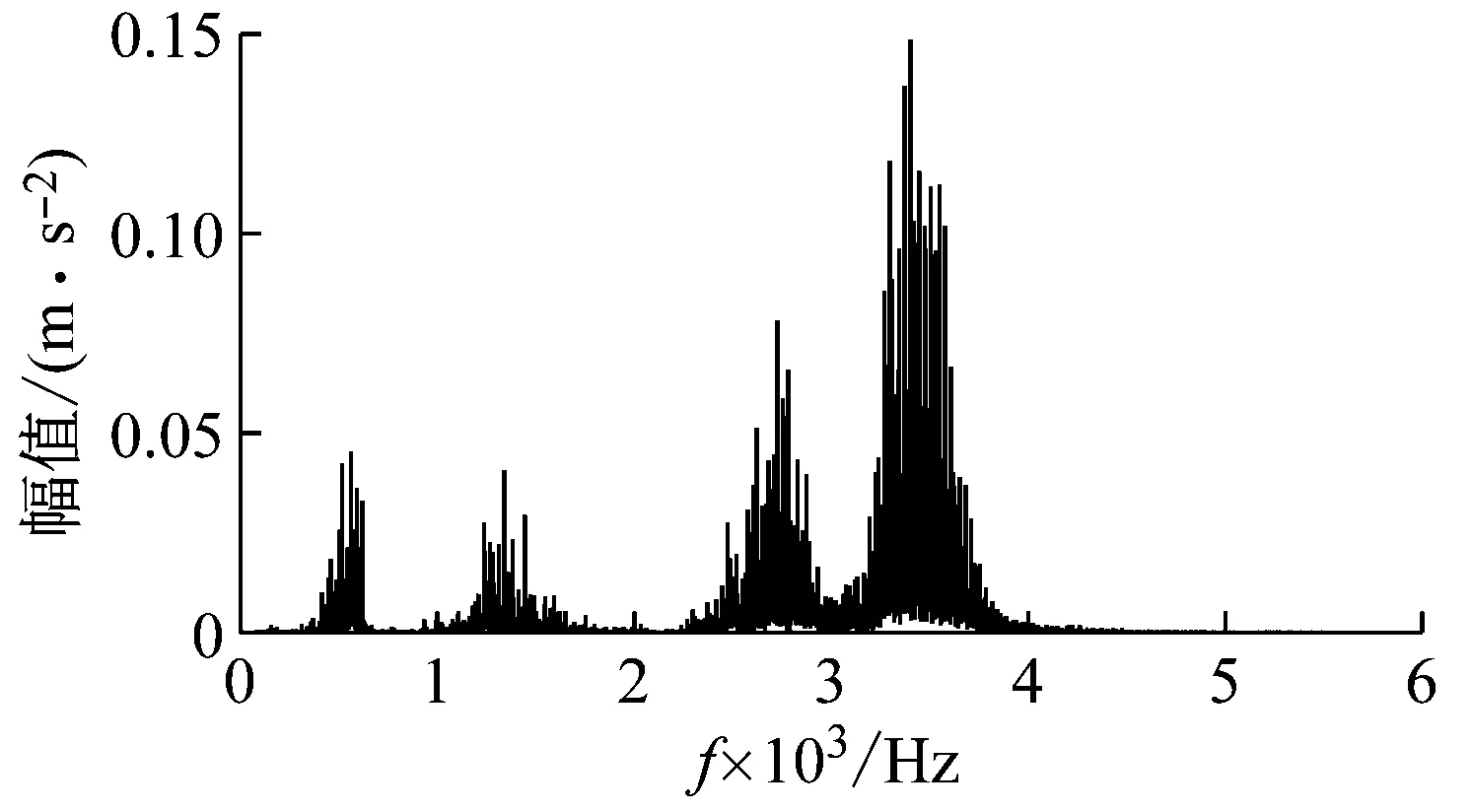
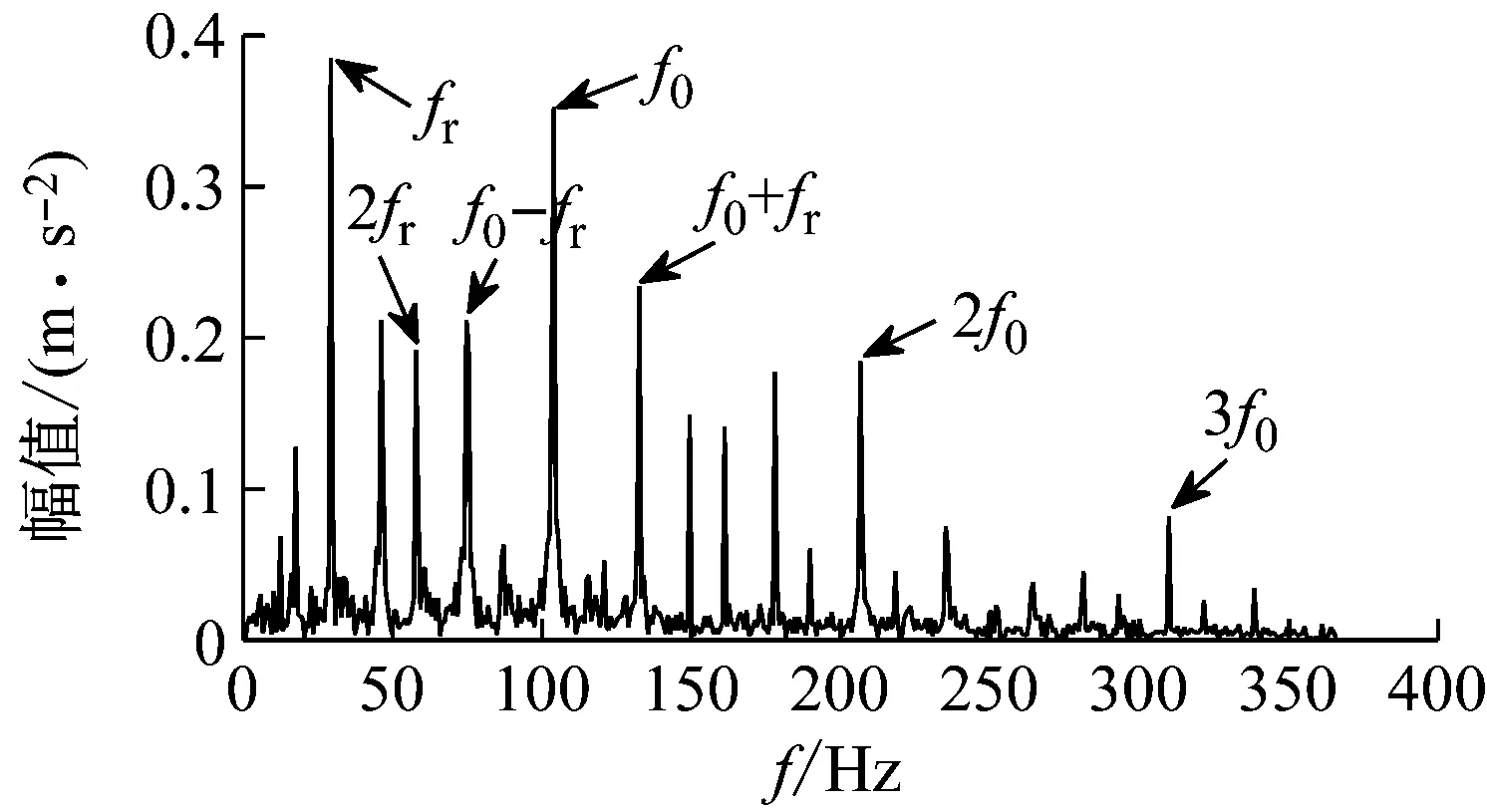
(2) 各模态分量相关系数ri分别与阈值r0进行比较,如果ri≥r0,对应的模态分量归于有效模态组{uv1,uv2,…,uvp};如果ri (3) 当含噪模态组{un1,un2,…,unq}只有1个模态分量时,直接去掉该模态分量;有两个及以上模态分量时,因相关系数最小的模态分量unq与原始信号关联性最弱,通常为噪声干扰信号,将其先去除,含噪模态组变为{un1,un2,…,un(q-1)},针对该含噪模态组按1.3节方法进行小波阈值去噪处理,其中,设定小波基函数为db8、小波分解层数为5层、小波阈值公式如下 (19) 式中:N为信号长度;σ为信号噪声方差,其计算式为 σ=median(|Wj,k|)/0.674 5 (20) 式中,Wj,k为信号分解后得到的小波系数。 (21) 本文采用的信号降噪结果评价指标包括:信噪比SNR、能量百分比ESN、均方根误差RMSE以及波形相似系数NCC。 信噪比SNR计算式如下 (22) 式中:x(t)为含噪信号;x′(t)为降噪后信号;N为数据点数。SNR值越大表示降噪效果越好。 能量百分比ESN计算式如下 (23) 式中:E′为降噪后信号能量;E为含噪信号能量,ESN值越大表示降噪效果越好。 均方根误差RMSE计算式如下 (24) RMSE值越小表示降噪效果越好。 波形相似系数NCC计算式如下 (25) NCC值越大表示降噪效果越好。 基于滚动轴承外圈故障机理与信号特征,构建了式(26)所示仿真信号[20] (26) 式中:x(t)为轴承外圈故障含噪信号;y(t)为不含噪信号;x1(t)为共振干扰脉冲信号,设fr为轴转频,取fr=18 Hz,则相应的干扰脉冲间隔周期T1=1/fr=0.056 s;x2(t)为外圈故障脉冲信号,设f0为外圈故障频率,取f0=107 Hz,则相应的故障脉冲间隔周期T2=1/f0=0.009 3 s;s(t)为谐波信号,其幅值取B0=0.4 m/s2;n(t)为高斯白噪声信号;Ai为调频信号,其频率为fr,幅值取B1=0.6 m/s2;C为衰减系数,取C=800;fn为系统固有频率,取fn=2 300 Hz。仿真信号采样频率设为12 000 Hz,采样点数为16 384个。 图3为不含噪仿真信号y(t)的时域波形、幅值谱和包络谱图,图4为含噪仿真信号x(t)的时域波形、幅值谱和包络谱图。由图3可知,不含噪声仿真信号外圈故障特征明显,尤其是包络图上,轴转频fr(18 Hz)、2倍频2fr(36 Hz)、3倍频3fr(54 Hz),外圈故障频率f0(107 Hz)、2倍频2f0(214 Hz)、3倍频3f0(321 Hz)、4倍频4f0(428 Hz),以及以故障特征频率f0为中心、以转频fr为边带的各种调制频率成分f0+fr(125 Hz)、f0-fr(89 Hz)、2f0+fr(232 Hz)、2f0-fr(196 Hz)等清晰可见,易于故障判定。由图4可知,由于叠加了较强的高斯噪声,外圈故障特征几乎被淹没,体现在图4(c)的包络谱图上,几乎无法提取出外圈故障特征频率。 (a) 时域波形曲线 (b) FFT频谱图 (c) 包络谱图图3 不含噪仿真信号y(t)Fig.3 Simulated signal y(t) without noise (a) 时域波形曲线 (b) FFT频谱图 (c) 包络谱图图4 含噪仿真信号x(t)Fig.4 Simulated signal x(t) with noise 针对含噪仿真信号x(t)分别进行EMD和本文方法的降噪处理。图5(a)为EMD分解得到的每个IMF分量时域波形,图5(b)为每个IMF分量对应的FFT频谱图。由图5可见,EMD分解结果中存在较为严重的模态混叠现象,各模态分量的频段分离效果较差,以IMF2为例,系统固有频率fn及其边频带和其他中低频率成分混叠在一起,不能有效提取有用信息;IMF2~IMF5,相邻的IMF之间均产生了模态混叠,每个IMF均包含了低频成分。与此同时,EMD分解过程中产生了虚假分量,如IMF3和IMF4中对应的频率成分并不存在。 (a) IMF时域波形曲线 (b) IMF频谱图图5 含噪仿真信号EMD分解Fig.5 EMD decomposition of simulation signal with noisy 利用本文提出的方法,首先进行基于IPSO算法的K和α参数寻优,K和α的寻优范围设置为[3,10]和[200,6 000],获得的最优参数值K=5,α=2 182;基于该最优参数进行VMD分解,得到的各IMF分量时域波形如图6(a)所示,各IMF分量对应的FFT频谱如图6(b)所示。由图6可见,本文方法可有效去除模态混叠现象,含噪信号经分解后实现了信号频域及各个IMF分量的自适应剖分,每个IMF都围绕在某一中心频率处,轴转频成分被分解到IMF1,系统固有频率fn被分解到IMF3,而系统固有频率fn边频带则被分解到IMF2和IMF4上,噪声成分被分解到IMF5中;同时该方法也避免了虚假模态的产生。由此可见,相较于EMD算法,本文方法具有更好的分解效果与噪声鲁棒性。 (a) IMF时域波形曲线 (b) IMF频谱图图6 含噪仿真信号VMD分解Fig.6 VMD decomposition of simulation signal with noisy 分别针对EMD和本文方法分解得到的各IMF分量与含噪仿真信号x(t)进行互相关计算,得到的互相关系数r如表1所示。 表1 各IMF分量与x(t)的互相关系数riTab.1 Cross correlation coefficient ri between each IMF component and x(t) 根据式(18)确定相关系数阈值r0,然后对表1中满足系数阈值条件的IMF 进行信号重构。经计算,EMD分解的各模态函数分量r0=0.16,本文方法分解的各模态函数分量r0=0.17。因此,结合表1,EMD分析结果中选取IMF1、IMF6,其他各模态函数分量舍弃,以此重构信号;本文方法分析结果中将IMF1、IMF2、IMF3、IMF4归为有效模态组,IMF5归为含噪模态组,由于含噪模态组只有1个分量,不用进行小波阈值处理,直接舍弃,以有效模态组4个分量重构信号。最终得到2组降噪后信号,分别示于图7和图8。图7(a)是EMD降噪信号时域波形,图8(a)是本文方法降噪信号时域波形,与图3(a)不含噪仿真信号y(t)的时域波形相比,可定性看出EMD降噪后仍存在一定程度上的噪声干扰,本文方法降噪信号波形比EMD降噪更接近不含噪仿真信号。图7(b)和图8(b)是两组降噪后信号的包络谱图,与图3(c)不含噪仿真信号y(t)的包络图均极为接近,故障频率f0及其各种调制频率等特征频率清晰可见。 (a) 时域波形曲线 (b) 包络谱图图7 EMD方法降噪结果Fig.7 Noise reduction results of EMD method (a) 时域波形曲线 (b) 包络谱图图8 本文方法降噪结果Fig.8 Noise reduction results of this paper method 应用式(22)~式(25),针对降噪后信号进行降噪指标计算,结果如表2所示(表中还列出了EEMD评价结果)。可以观察到本文方法降噪结果信噪比更高、能量百分比更大、均方根误差更小、平滑度更接近1,各项评价指标全面好于EMD和EEMD方法,说明本文方法降噪效果明显优于EMD和EEMD降噪方法。 表2 降噪评价指标结果Tab.2 Evaluation index results of noise reduction 采用美国凯斯西储大学的滚动轴承故障试验数据验证本文降噪方法的有效性,试验系统如图9所示。 图9 滚动轴承试验台Fig.9 Rolling bearing test bench 实验台驱动端轴承型号为6205-2RS JEM SKF深沟球轴承,技术参数和规格信息如表3所示。 表3 滚动轴承技术参数和规格信息Tab.3 Technical parameters and specifications of rolling bearing 采用电火加工技术分别在轴承内、外圈布置单点故障,选择驱动端轴承外圈故障数据,故障直径为0.533 4 mm,深度为0.279 4 mm。该外圈故障对应电机转速为1 721 r/min(即转频fr为28.68 Hz),采样频率为12 000 Hz,采样点数为16 384。结合表3中轴承各参数,通过下式计算得到轴承外圈故障频率f0为102.81 Hz。 (27) 试验采集到的原始故障信号相关信息如图10所示,其中图10(a)是其时域波形曲线,图10(b)是其FFT分析幅值谱图,图10(c)是其包络谱图。由图可知,故障时域波形冲击特征较为明显,但也存在大量噪声;幅值谱图上谱线主要分布在4个频段区域:高频区(中心频率约3 400 Hz)、次高频区(中心频率约2 800 Hz)、中频区(中心频率约1 300 Hz)和低频区(中心频率约600 Hz),信号能量主要集中在高频和次高频区,低频区的能量较小,而轴承的外圈故障特征频率几乎无法提取;包络图上能观察到轴转频和故障特征频率,但由于噪声干扰,图上干扰谱线较多,故障特征频率的调制频带等故障相关频率成分均很难观察到。 (a) 时域波形曲线 (b) FFT频谱图 (c) 包络谱图图10 试验原始信号图形Fig.10 Experimental original signal graph 利用本文方法,通过IPSO算法获得VMD最优参数值K=7,α=2 684,进一步对原始故障信号进行VMD分解,得到的各IMF分量时域波形如图11(a)所示,对应的FFT幅值谱如图11(b)所示。将各IMF分量与原始信号进行互相关计算,得到的互相关系数如表4所示。 表4 各IMF分量与原始信号的互相关系数Tab.4 Cross correlation coefficient between each IMF component and original signal (a) IMF时域波形曲线 (b) IMF频谱图图11 试验原始信号VMD分解Fig.11 VMD decomposition of test original signal 结合图11和表4可以看出含噪信号经VMD分解后实现了信号频域及各个IMF分量的自适应剖分,每个IMF都围绕在4个频段区域的某一中心频率处,低频段区被分解到IMF1和IMF2,二者有一定的频率重叠,其互相关系数值也较小,中频段区被分解到IMF3,次高频段区被分解到IMF4,高频段区由于能量占比最大,它被分别分解到IMF5、IMF6和IMF7,其互相关系数值也最大。 由式(18)可确定相关系数阈值r0=0.18,结合表4,将IMF4、IMF5、IMF6、IMF7归为有效模态组,IMF1、IMF2、IMF3归为含噪模态组,其中IMF2相关系数最小,直接舍弃,对含噪模态组的IMF1和IMF3进行小波阈值处理,并与有效模态组的4个IMF分量一起重构信号,得到降噪信号,其时域波形、FFT幅值谱、包络谱示于图12。与试验原始信号图10相比,降噪后时域波形冲击特征更明显,幅值谱能量分布基本不变,噪声干扰更少,谱线更清晰;降噪效果在包络谱图12(c)上体现最明显,其谱图较为干净,干扰成分较少,可清晰发现轴转频fr(约29 Hz)、2倍转频2fr(58 Hz)成分,也可发现明显的约103 Hz故障区域,对应轴承外圈故障频率f0,同时存在故障频率的2倍频2f0(206 Hz)、3倍频3f0(309 Hz)成分,以及以故障特征频率f0为中心以转频fr为边带的调制频率成分f0+fr(132 Hz)和f0-fr(74 Hz),这与外圈故障特征频率被转频所调制的特性相符。说明本文方法有很好的降噪效果,据此提取的故障特征可用于轴承外圈故障的判定。 (a) 时域波形曲线 (b) FFT频谱图 (c) 包络谱图图12 降噪后信号图形Fig.12 Signal graph after noise reduction 本文针对滚动轴承强背景噪声故障信号,提出了一种基于参数自寻优变分模态分解的信号降噪方法。为实现VMD模态数K和二次惩罚因子α的自适应寻优,提出了一种改进粒子群算法(IPSO),通过构建适合滚动轴承故障信号特点的适应度函数、惯性权重公式、边界粒子以及粒子群优化处理方法,提高了VMD参数自寻优搜索能力;基于最优K和α,对含噪信号进行VMD分解,利用相关系数筛选法,对K个IMF分量进行有效模态和含噪模态识别,对后者进行小波阈值去噪,并与前者一起进行信号重构,实现信号降噪。从数值仿真和试验数据角度,将本文所提方法与EMD和EEMD降噪方法进行对比分析,从信噪比、能量百分比、均方根误差以及波形相似系数4个评价指标,定量说明本文方法在滚动轴承故障信号降噪中具有更好的降噪效果,是一种有效的降噪方法。
4 仿真信号降噪分析
4.1 降噪评价指标
4.2 仿真信号构建
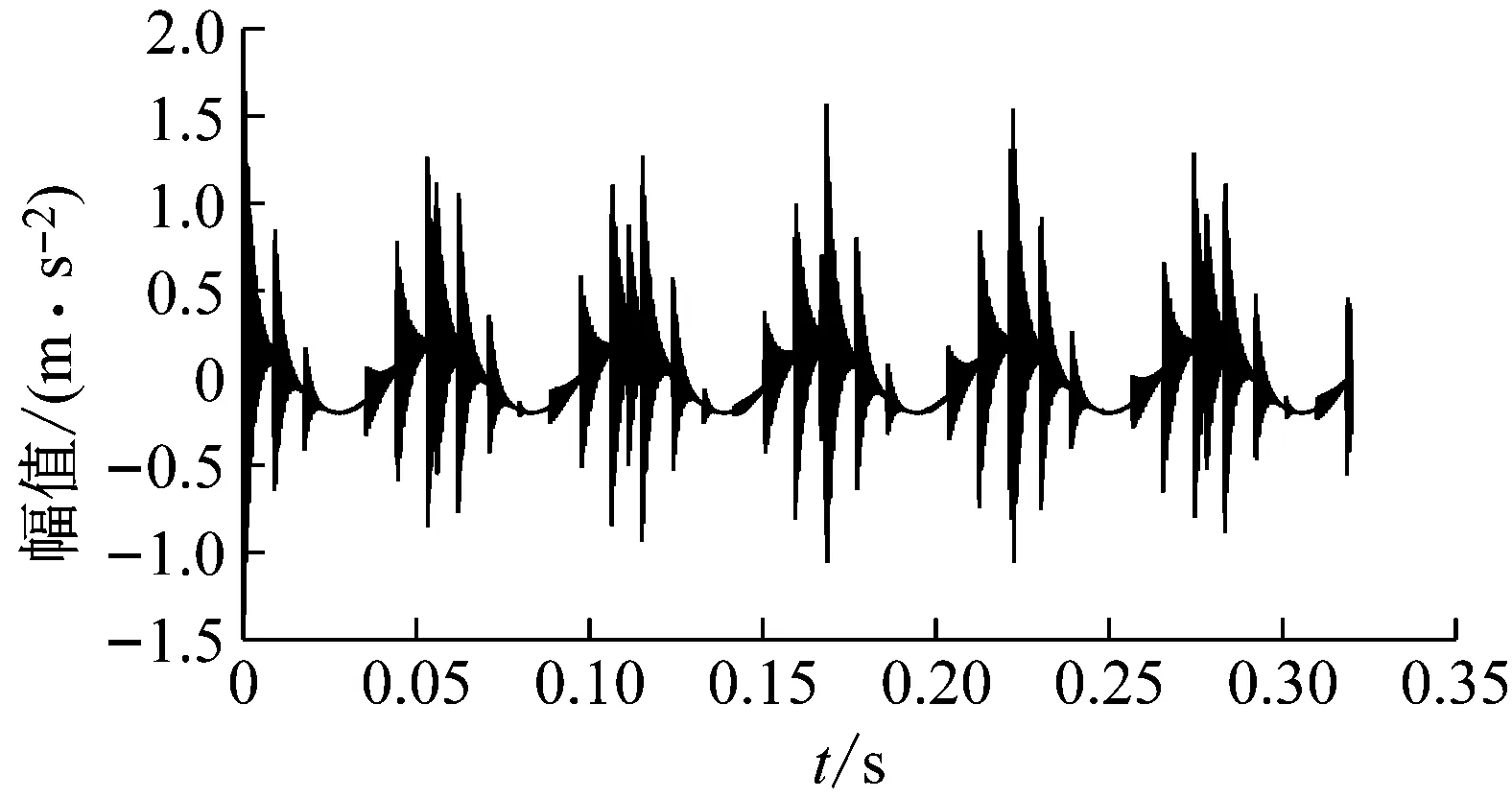

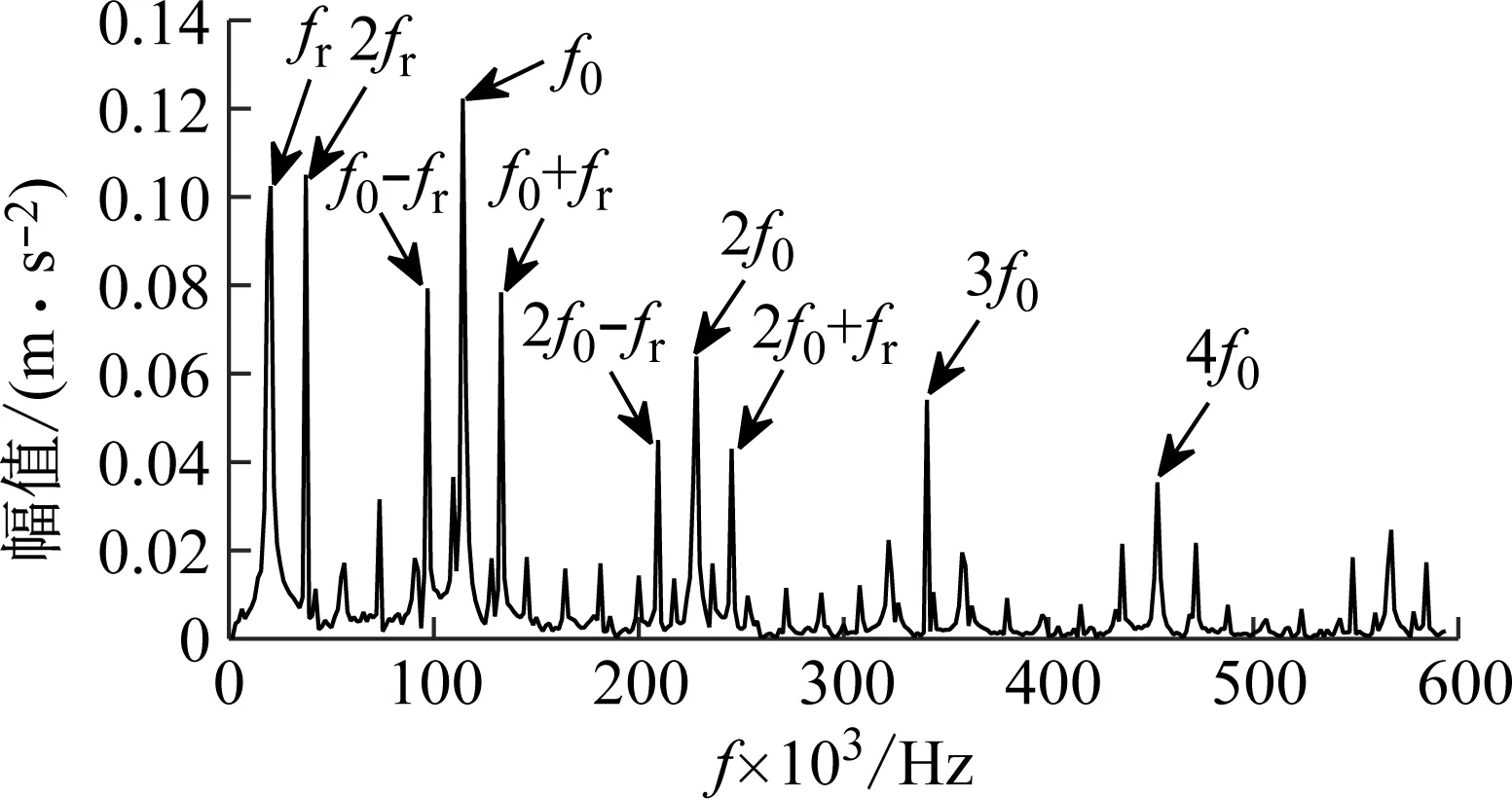
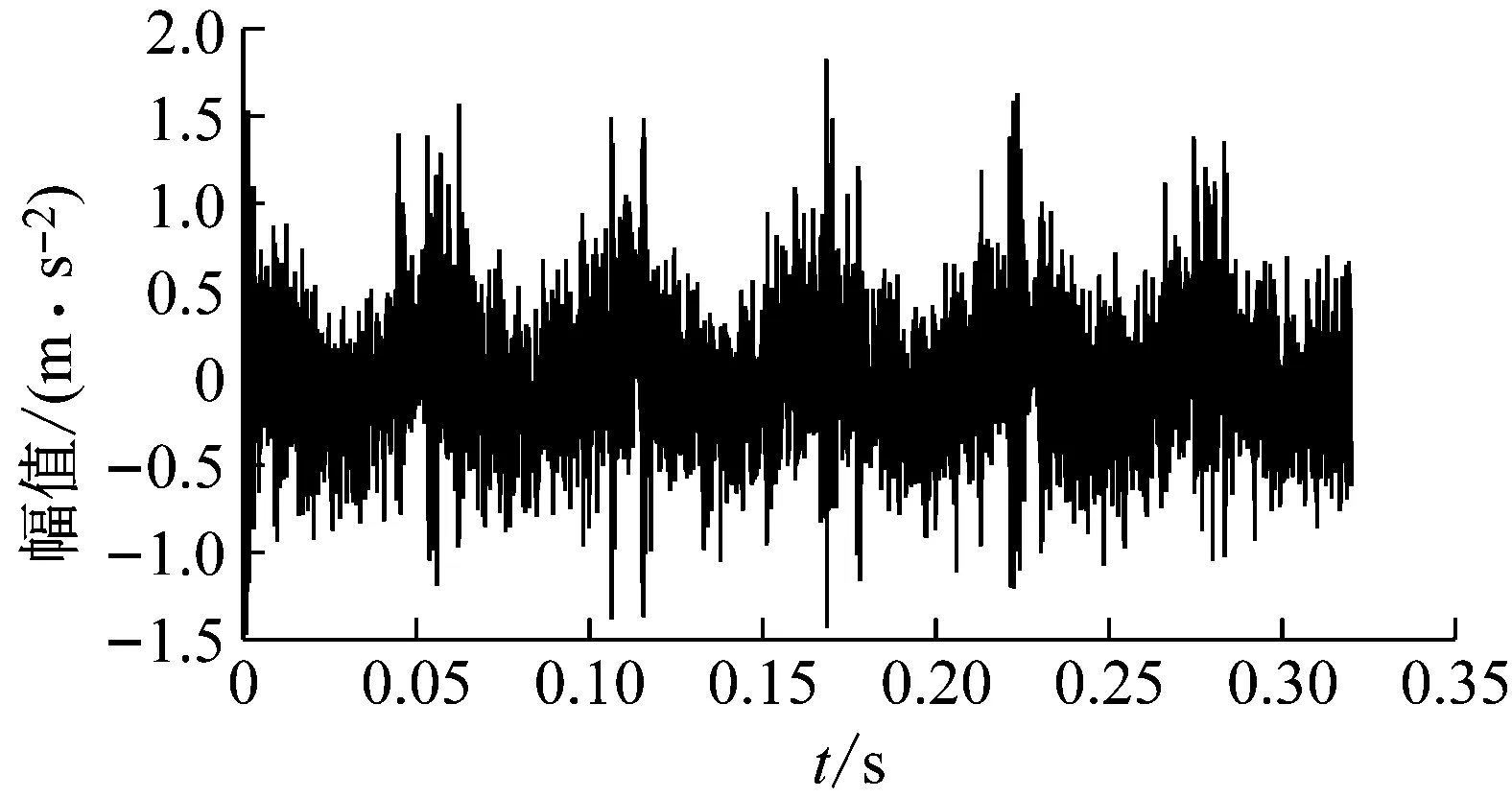
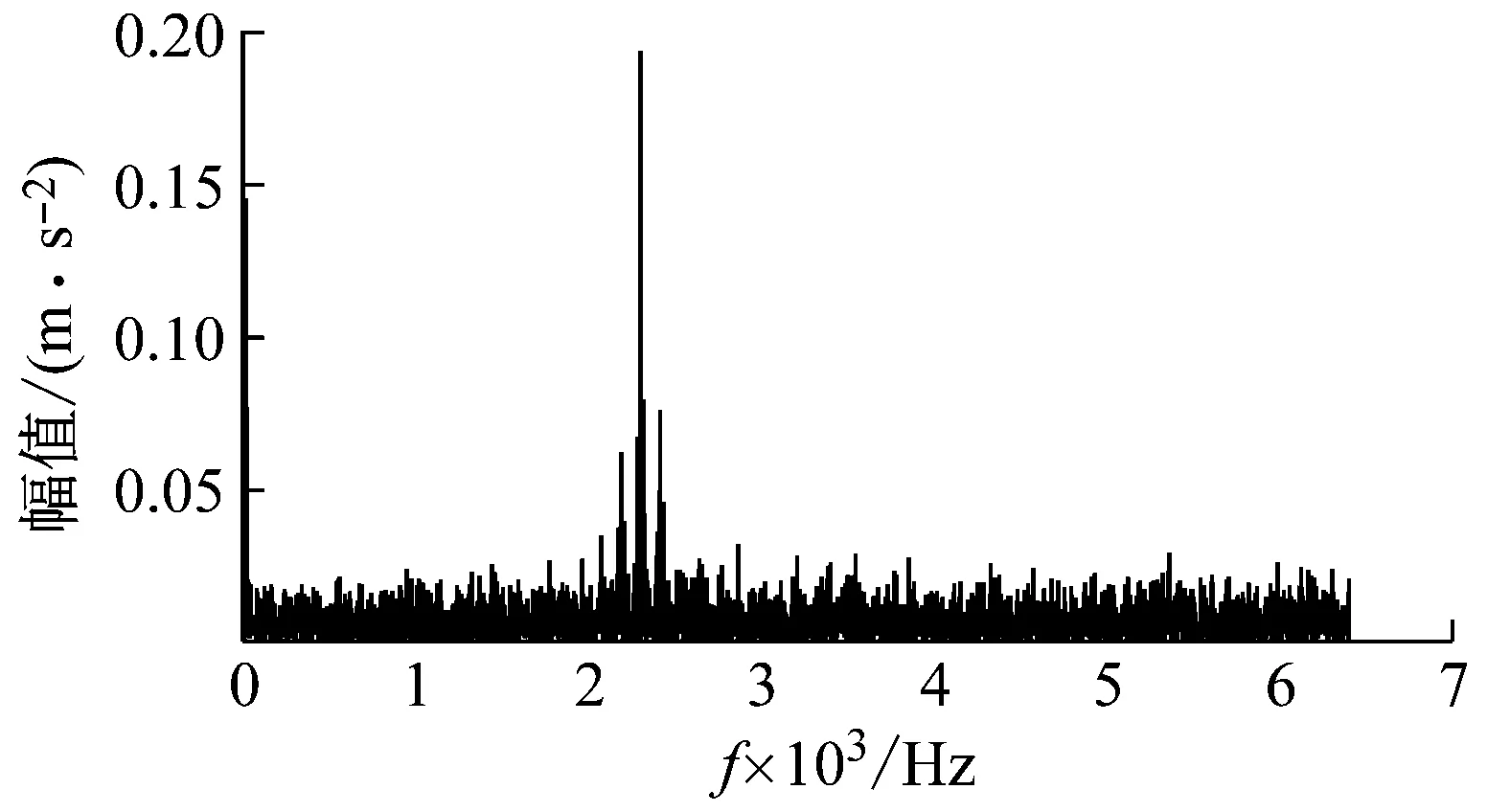
4.3 仿真信号分析


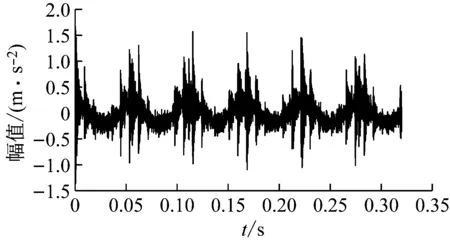

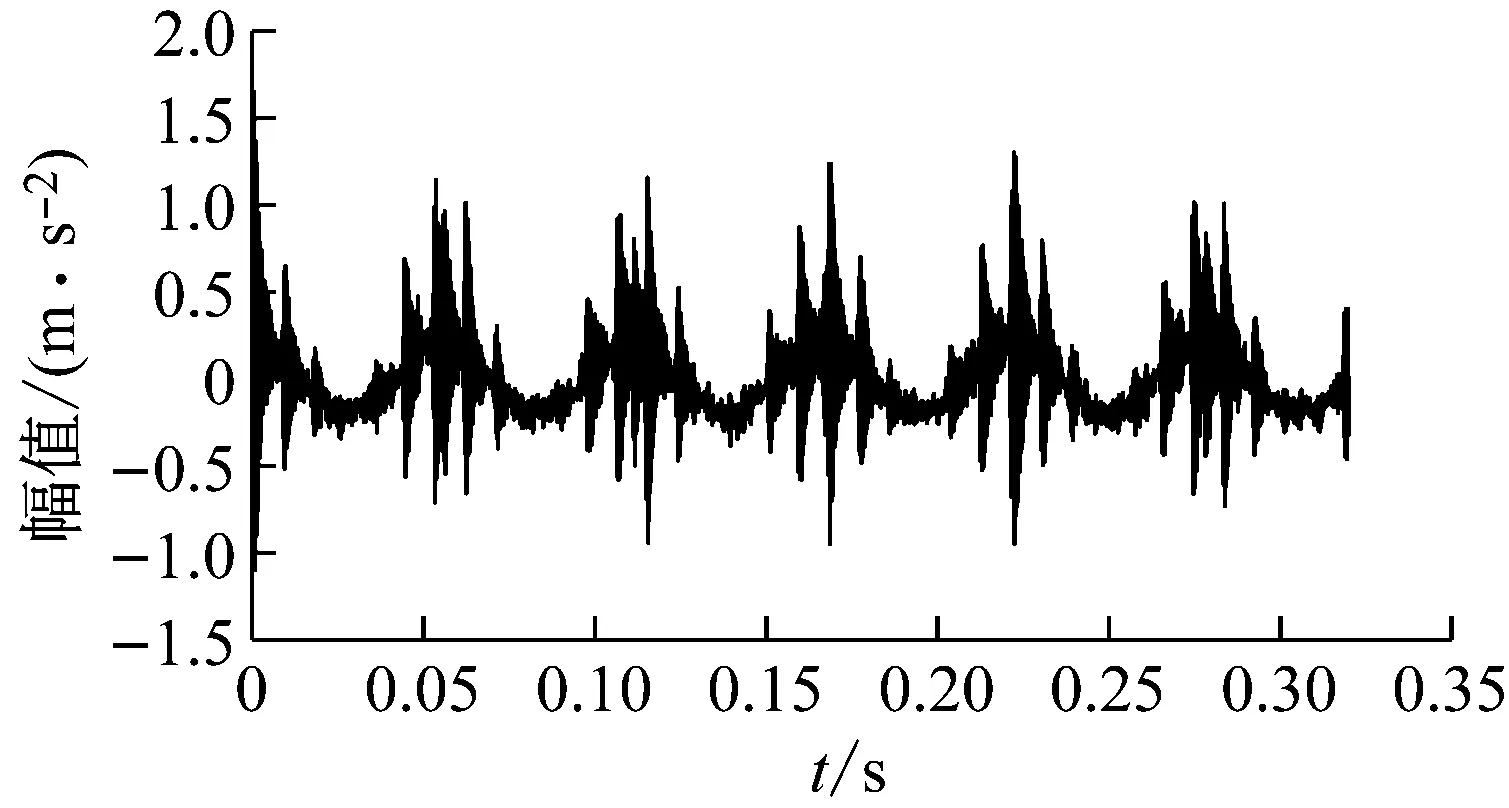
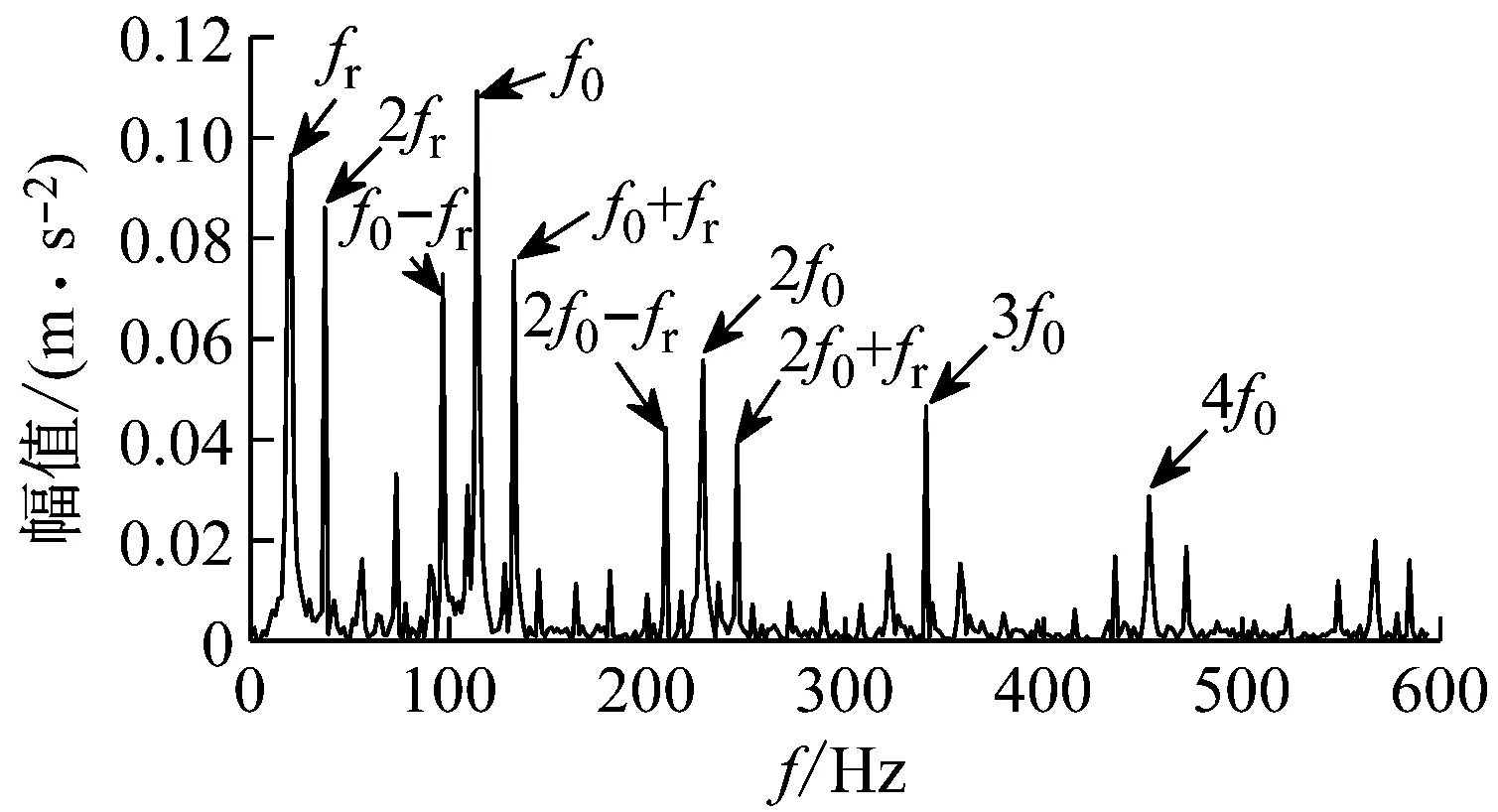
5 试验信号降噪分析





6 结 论

