光电专业光子气体黑体辐射理论的教学实践
陈培锋,王铭海
(华中科技大学 光学与电子信息学院,湖北 武汉 430074)
黑体辐射理论是理解光源特性、光电探测系统、发光和激光等技术的理论基础,所以在光电专业教学中具有重要意义. 但是关于黑体辐射的教学却分散在大学物理[1]、光电探测[2]、激光原理[3]等多门课程中. 在这些课程中的教学主要是直接给出黑体辐射的普朗克公式,一般不加推导. 随着固体发光材料的发展,关于固体物理的教学逐渐显得重要,因此近年来在光电专业逐渐开始开设“热力学统计物理”和“固体物理”课程. 在热力学统计物理课程中,黑体辐射主要是通过平衡热辐射的光子气体理论[7]进行介绍. 通过多年的实践,笔者认为在光子气体理论教学中,将光电专业相关理论加以系统介绍,对于光电专业学生系统理解本专业关于物质相互作用的基础是很重要的. 本文的介绍围绕光子气体理论的教学程序和实践经验,其中的一些实践经验与论文[4]可以相互印证.
1 黑体辐射与基尔霍夫定律
热辐射、黑体辐射的基本概念在大学物理[1]中已经系统介绍,这里只需要简单回顾. 对于光电专业学生进一步从光源的发光概念引出黑体辐射是有必要的. 实践表明,通过介绍基尔霍夫定律引出黑体辐射的重要性,是光电专业教学比较好的切入点[4]. 而基尔霍夫定律分析的是物体热辐射的能力,所以也是光电专业学生学习光电探测技术的基础,这样切入可以很好体现光电专业基础课的特点.
首先物体的辐出度和单色辐出度[2]可表示为[5]
R(T)=ε(T)Rb(T),Rλ(T)=ελ(T)Rλb(T)
(1)
其中ε(T)和ελ(T)为物体的发射率和单色发射率,而Rb(T)和Rλb(T)是黑体的辐出度和单色辐出度.由此可见,实际物体的辐射能力是通过与黑体比较表征的,由此可见黑体辐射理论对光电专业的基础作用.
其次,基尔霍夫在1859年总结出了一个普遍的规律(基尔霍夫定律):任何物体在同一温度T下辐出度R(T)和吸收率α(T)成正比,比值等于同温度下黑体的辐出度Rb(T);任何物体在同一温度T下单色辐出度Rλ(T)和吸收率αλ(T)成正比,比值等于同温度下黑体的单色辐出度Rλb(T),只和频率ν、温度T有关,与物质本身性质无关.

(2)
比较式(1)、(2),可见
ελ(T)=αλ(T)
(3)
这表明,物体的发射率等于同温度下物体的吸收率.对于光电探测领域的学生,建立起一个物体“具有高的吸收率同时必然具有高的发射率”这个基本观念很重要的.因为基尔霍夫定律正是热力学平衡态的理论结果,所以在讲解光子气体统计课程时进行介绍是非常合适的.
2 普朗克关于空腔中平衡辐射的最初探索以及瑞利-金斯公式的引出
一般介绍瑞利-金斯公式时,会直接给出空腔中电磁模式数的结果[6],然后类比能量均分原理假设每个电磁模式的平均能量为kT,最后给出瑞利-金斯公式.
实际上根据历史发展进程,先介绍普朗克关于平衡热辐射的谐振子理论,更有利于学生理解,并且更容易使学生建立起辐射与腔壁物质辐射的关系.因为腔壁中的谐振子的能量本身就是统计物理已经解决的问题,这比硬性地引入电磁辐射的平均能量更合理.

(4)
其中ρ为空腔中辐射能量密度,U为腔壁谐振子平均能量,ν为振子频率,c为光速.普朗克认为既然空腔平衡辐射与腔壁的物质无关,那么假设空腔是由谐振子组成的是成立的.在这个基础上由运动方程出发,根据谐振子的电磁辐射和吸收的规律,当谐振子与空腔辐射达到热平衡时推出了上式.
式(4)的重要性在于,实际考虑到了腔壁与热辐射之间的热平衡,并且只要确定了腔壁谐振子在温度T时的平均能量U, 就可以得到空腔平衡辐射的能量分布规律.正如文献中指出[8,9],如果普朗克采用当时已为人们熟知的、经典统计学中的能量均分定理, 即U=kT,那他就于1899年5月得到了一年之后由瑞利得到的瑞利公式.
教学实践中表明,如果不介绍普朗克的这个工作,那么讲到瑞利公式的时候,只能如文献[10]认为的那样,将腔壁的谐振子模糊处理为空腔辐射中的模式.由于8πν2/c3确实等于单位体积空腔中的谐振模式数,所以作这样的模糊处理学生一般不会提出疑问.但这是不严谨的,因为无法体现出空腔中平衡热辐射的来源,也无法表现出空腔辐射与腔壁的热平衡条件,同时后续的谐振腔量子化也非常勉强.同时如果模糊腔壁谐振子与空腔辐射之间的区别,那就意味着普朗克最先提出了辐射场的量子化假设,这与爱因斯坦在1905年提出辐射量子化相矛盾.正是因为这种种原因,以腔壁谐振子为基础,通过式(4)讲解瑞利公式和普朗克量子化是应该被提倡的.
在式(4)的基础上进一步讲解瑞利公式就很简单了.根据经典物理的能量均分原理,处于温度T平衡态的谐振子的平均能量为kT,代入式(4)即得单位体积空腔中能量密度为
(5)
这就是大家都熟悉的瑞利-金斯公式[7].由此引出经典物理的困难.由于上述从式(4)引入的过程建立在严格的经典物理基础上,所以这种困难存在是不可克服的,如果在推导过程中引入了模糊的处理,学生就会感到疑惑.
3 关于普朗克公式和量子化
关于普朗克采用数学上的内插法获得普朗克公式的过程,以及随后的分立能级的提出,这在目前的教学体系中是比较成熟的,很多文献都专门讨论了教学的方法[4,6].
笔者认为,引入普朗克之前的工作式(4),教学中会更加严谨.因为如果明确普朗克考虑的是腔壁谐振子的平均能量,则根据定域子的统计特性,腔壁谐振子自然应该满足玻耳兹曼统计.这样普朗克通过量子化能级的玻耳兹曼统计分布获得的谐振子平均能量就有了严格的依据.如果不引入腔壁谐振子的概念,将其模糊处理为辐射谐振模式,学生会对其应满足的统计规律产生疑问.因为我们后面是通过光子的玻色统计引入了谐振模式的能量,学生会对为什么两种统计获得相同的结果产生怀疑.
关于普朗克公式及其量子化过程的教学虽然成熟,但正确地引入腔壁谐振子的概念,仍然会极大地提升学生的学习体验,对于学生严谨科学态度的养成是非常有益的.
4 光子气体理论
关于空腔中平衡热辐射的理论核心,采用光子气体理论是最为简洁的,特别适合于学生长期的记忆和推导.同时光子气体作为玻色子的概念引入,对于学生后续课程中认识激光器中大量光子占据相同的光子态,以及这些具有相同光子态的光子的“具有相同的特性”会有更深刻的认识,对具有相同光子态的光子组成的激光的特性也具有更深刻的认识.关于其讲授,笔者实践中认为采用《热力学统计物理》[7]的讲授方法学生是很容易接受的.
笔者实践中认识到,在教学过程中应该特别强调空腔热辐射实际上仍然与黑体辐射是有区别的.按照黑体的定义,空腔小孔辐射才是黑体辐射的模型,因此黑体辐射与空腔热平衡辐射之间的区别需要明确.
光子的自旋态数为2,则在体积为V的空腔中,在p→p+dp动量范围内的光子态数为
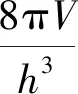
(6)
考虑到ε=cp=ћω可得在圆频率ω→ω+dω范围内光子的量子态数为

(7)
光子满足光子数不守恒的玻色分布,在圆频率ω→ω+dω范围内的平均光子数为
(8)
在圆频率ω→ω+dω范围内每个光子具有ћω的能量,因此可得平衡热辐射场能量为
(9)
这就是空腔中平衡热辐射场的普朗克公式[7].
而黑体辐射则可以用光子碰壁的概念直接根据碰壁数[7]或泻流[5]的概念引出.单位时间内打到单位面积壁上圆频率在ω~ω+dω区间的光子数为
(10)
单位时间穿出器壁上单位面积圆频率在ω~ω+dω区间内的能量为
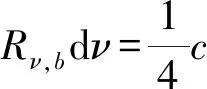
(11)
这对应着正确的黑体辐出度公式[1]:
(12)
许多教材混淆了式(11)、(12)与(9),虽不至于引起大的误解,但对专业的学生还是需要严格求证的.
5 爱因斯坦的辐射理论[3]
光子气体理论虽然直接可以推出空腔平衡热辐射的公式,过程简洁易掌握.但是严格意义上说,由于光子间不存在相互作用,所以这个理论无法解释平衡热辐射的平衡过程.只有引入腔壁的辐射和吸收,光子气体通过与腔壁达到热平衡,才能够解释光子气体的平衡过程.这样似乎又回到了本文最开始普朗克考虑的问题.但是现代的原子理论已经不再是普朗克当时的状态,因此爱因斯坦在1916年提出了受激辐射的概念.只有提供爱因斯坦的受激辐射理论的教学才能够真正将关于空腔热平衡辐射的理论比较完整地讲授.而受激辐射理论对于光电专业的学生是非常重要的,借这个教学机会将其介绍给学生也具有重要的意义.
要弥补上述光子气体理论推导过程中的缺陷,需要将空腔的壁同时考虑进去.光子气体是通过与空腔壁的相互作用达到热平衡的.即使是达到热平衡,空腔中的光子不断被壁吸收,但同时壁也会不断地辐射光子,当单位时间里壁吸收的光子与辐射的光子达到平衡时,空腔中的辐射场就是平衡热辐射场.最早考虑这个问题的是爱因斯坦,爱因斯坦通过这样的模型在1917年提出原子受激辐射概念.
考虑谐振频率为ν的平衡辐射场ρν与空腔壁原子的相互作用.为简化起见,只考虑原子的2个谐振能级E2和E1,并有E2-E1=hν
(13)
单位体积内处于2能级原子数分别用n2和n1表示.
波尔提出了原子的自发辐射跃迁和受激吸收跃迁过程.考虑到腔壁原子为定域子,应满足玻耳兹曼分布,而空腔中的平衡热辐射分布式(9)与玻耳兹曼分布存在明显不同,爱因斯坦提出,辐射场ρν与物质原子的相互作用还应包含受激辐射跃迁过程,据此可以进一步定义3个跃迁过程的速率[3].
处于高能级E2的一个原子自发地向El跃迁,并发射一个能量为hν的光子,称为自发跃迁过程.自发跃迁过程用自发跃迁概率A21描述.Δt时间内自发辐射跃迁的原子数正比于n2:
(Δn21)sp=A21n2Δt
(14)
A21定义为单位时间内n2个高能态原子中发生自发跃迁的原子数与n2的比值.如果空腔壁原子和辐射场相互作用只包含上述自发跃迁过程,是不能维持空腔内辐射场的稳定的.因此,必然还存在—种原子在辐射场作用下的受激跃迁过程.
处于低能态E1的一个原子,在频率为ν的辐射场作用(激励)下,受激地向E2能态跃迁并吸收一个能量为hν的光子,这种过程称为受激吸收跃迁.最朴素的想法显然是假设受激吸收跃迁几率W12与腔内辐射密度ρν成正比,因此Δt时间内受激吸收辐射跃迁的原子数正比于n1:
(Δn12)st=B12ρνn1Δt
(15)
比例系数B12称为受激吸收跃迁爱因斯坦系数,它只与原子性质有关.
爱因斯坦提出存在受激吸收跃迁的反过程——受激辐射跃迁.Δt时间内受激辐射跃迁的原子数正比于n2:
(Δn21)st=B21ρνn2Δt
(16)
比例系数B21称为受激辐射跃迁爱因斯坦系数,它只与原子性质有关.
根据上述相互作用物理模型分析空腔黑体的热平衡过程,可以导出爱因斯坦3系数A21、B12、B21之间的关系.
首先,在平衡态下,腔内的辐射场ρν遵守Planck的热平衡黑体辐射分布:
(17)
其次,空腔壁原子数按能级分布应服从热平衡状态下定域子的玻耳兹曼分布:
(18)
式中g2和g1分别是能级E2和E1的简并度.
最后,在腔内的辐射场ρν与腔壁物质原子达到共同平衡时,n2和n1应保持不变,即自发辐射和受激辐射引起的能级E2上粒子数n2的减少应等于受激吸收引起的粒子数n2的增加,即
(Δn12)st=(Δn21)st+(Δn21)sp
或
n2A21+n2B21ρν=n1B12ρν
(19)
联立上面3个平衡条件,得
(20)
要使上式恒等,需要
B12g1=B21g2
(21)
(22)
式(21)、(22)所代表的光子与物质能级的相互作用关系是普适的关系式,是激光原理[3]等课程的核心基础.
6 关于受激辐射的说明
6.1 受激辐射的存在性证明
假设不存在受激辐射,式(19)变为
n2A21=n1B12ρν
(23)
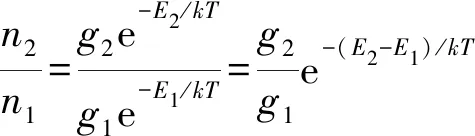
(24)
(25)
无法得到普朗克公式.
这个分布正好对应维恩分布[6,7],在忽略受激辐射过程的条件下,无法得到普朗克分布,因此受激辐射是必须存在的,只有这样才能解释普朗克分布.
6.2 受激辐射的特性
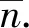
(26)
按照爱因斯坦理论,发射光波的另一条途径是受激辐射.但是,爱因斯坦受激发射理论发表后的很多年后人们才发现其真正的应用意义.
造成这种状况的原因是当物质处于热平衡态时,能级上的粒子数(或称粒子集居数或布居数)服从MB分布,为简单起见令g2=g1,因此有

(27)
由于E2>E1,所以n2 平衡态的理论已经如此深地占据了人们的思想,以至科学家宁可提出负吸收的概念解释光的放大,也没有想到光的放大实际是具有应用意义的.人们对非平衡态认识的局限性,使得受激辐射的理论只在理论物理学家建立光的散射、折射、色散和吸 收的量子理论时派上了用场,也由于对相干辐射源的需要当时也没有那么迫切,几乎没有人想到负吸收可以用在相干放大电磁波的工作器件上. 现在我们知道,在一定条件下,物质的光吸收可以转化为光放大,其条件为n2>n1,这一条件称为集居数反转. 当然这样必须打破热平衡状态,只有通过外界向物质不断供给能量(称为泵浦过程),集居数反转才能实现. 这已经成为激光发射的基础. 本文作者多年在光电专业讲授激光原理和光电技术课程,在此基础上通过开设光电专业统计物理课程,认识到其对于光电专业的重要性. 笔者根据自身的实践,认识到将辐射的黑体辐射对于光源辐射的基础作用和受激辐射概念等内容,系统地通过与光子气体理论结合的方法讲授给学生,可以保证光电专业学生对光与物质相互作用的理论有系统的理解;同时也通过实践体会到在讲授过程中需要注意一些细节的把握,这些细节对于学生严谨科学态度的养成是非常重要的.7 总结与思考

