Caputo导数的一种高精度算法及其在扩散现象中的应用
吴娟,张华,罗卫华
(1. 湖南文理学院信息与现代教育技术中心,湖南常德,415000;2. 湖南文理学院数理学院,湖南常德,415000)
近年以来,分数阶导数作为一个新的数学工具,已经在诸多科学研究领域得到了广泛的应用,特别是在高度复杂的介质当中,对相应的扩散行为作数值模拟时,分数阶导数能够提供更好的效果,相关结果可见文献[1-4]。
作为分数阶导数的一个重要成员,Caputo 导数算子
在时间分数阶领域已经得到了广泛的应用研究,这里 Γ(·)为Gamma 函数。而此类算子由于积分算子具有弱奇异性和非局部性,对其做数值离散是一个难题,这也是近年以来许多学者的重点研究对象。其中,高广花等在文献[5]中利用线性和二次的Lagrange 插值函数对式(1)进行离散,得到的数值方法具有局部的3-β阶精度,类似结果可见文献[6-9]。
本文利用二次Lagrange 插值函数构建式(1)的一种数值离散方法,给出所对应的数值递归公式,理论分析显示该方法可以达到全局的3-β阶数值精度,且能保证良好的数值稳定性。作为实际应用,本文将该类数值方法应用于时间分数阶扩散方程的数值求解中,并用数值算例加以验证。
1 数值离散
在区间 [t1,t3]采用过t1,t2,t3的二次Lagrange 插值函数,经过计算和化简可得t=t2处的离散格式为
其中A1,1=-2ρβ[1/(2-β)-1],A1,2=ρβ[1/(2-β)-1/2],δ1=ρβ[1/(2-β)-3/2],ρβ=1/(τβΓ(2-β))。
类似地,可以得到在t=t3处的离散格式为
其中A2,1=-22-βρβ[2/(2-β)-1],A2,2=2-βρβ[4/(2-β)-1],δ2=2-βρβ[4/(2-β)-3]。
对于区间 [t1,tk],(k=4,5,…,N+1):
(1)当k=2p时,将式(1)重写为对于项,采用过t1,t2,t3的二次Lagrange 插值; 对于项,采用过t2j,t2j+1,t2j+2的二次Lagrange 插值。经过计算和化简可得
(2)当k=2p+ 1时,将式(1)重写为对于项,采用过t1,t2,t3的二次Lagrange 插值; 对于项,采用过t2j+1,t2j+2,t2j+3的二次Lagrange 插值。经过计算和化简可得
综上所述,Caputo 导数算子(1)在所有网格点处的近似值可以由式(2)~(5)逐个求出。此外,关于数值格式(2)~(5)的可解性和逼近精度,有如下结论。
定理1对于任意的右端函数f(t)和初始值u1=u(t1),线性方程组
有唯一的解(u2,u3,…,uN+1)T。
证明首先,从式(2)、(3)可得二元线性方程组此方程组的系数矩阵的行列式为从而,结合右端项f(2t),f(t3)和初始值1u,由该方程组可以唯一求出解23T(u,u)。
其次,注意到cj,s≠0,dj,s≠0,(j=4,5,…,N+1,s=1,2,3),由式(4)、(5)可知: 当4≤k=2p≤N+1时,uk可以由式算出。当4k=2p+≤1≤N+1时,ku可以由式算出。
因此,对于任意右端函数f(t)和初始值u1=u(t1),线性方程组(6)有唯一解。定理证毕。
定理2对于任意的β∈(0,1),u(t)∈C3[0,T],数值格式(2)~(5)的误差总满足
证明由Lagrange 插值的误差理论知,对任意光滑函数u(t)和子区间[tk,tk+2],k=1,2,…,N-1,有u(t)-L[tk,tk+2](u(t))=u'''(ξk)(t-tk)(t-tk+1)(t-tk+2)/6,t∈[tk,tk+2],ξk∈(tk,tk+2)。
对于R(u(t2)),因为而由于
对于R(u(tk)),4≤k=2p≤N+1,将误差重写为并且利用分部积分法,可得
对于R(u(tk)),3≤k=2p+1≤N+1,可将误差重写为类似于k=2p的情形,可得。定理证毕。
2 数值算法在时间分数阶扩散方程中的应用
作为应用,本节利用上述数值离散格式(2)~(5)来求解如下时间分数阶扩散方程。
该方程是工程领域中模拟高度复杂介质下的流体扩散所涉及的一个数学模型,时间分数阶导数的介入,可以有效缓解整数阶导数算子所产生的重尾效应。对于模型(8)的数值模拟已经得到了一些计算数学研究者的广泛关注,其中文献[6,10-11]均取得了一些良好效果。
对于模型(8),时间方向用数值格式(2)~(5),空间方向用经典的紧差分格式进行数值求解。在下面的表1、2 当中,N表示时间方向的网格数,空间方向取定网格步长为1/128。为了体现收敛阶,取通用的误差计算公式这里E(N)表示网格数为N所对应的误差。
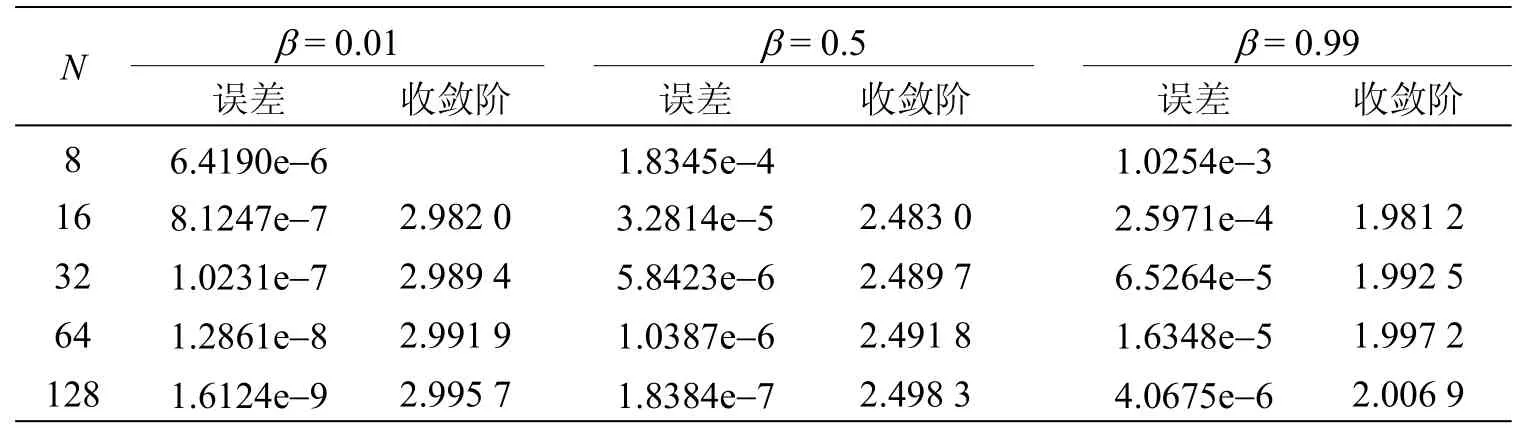
表1 例1 的数值结果
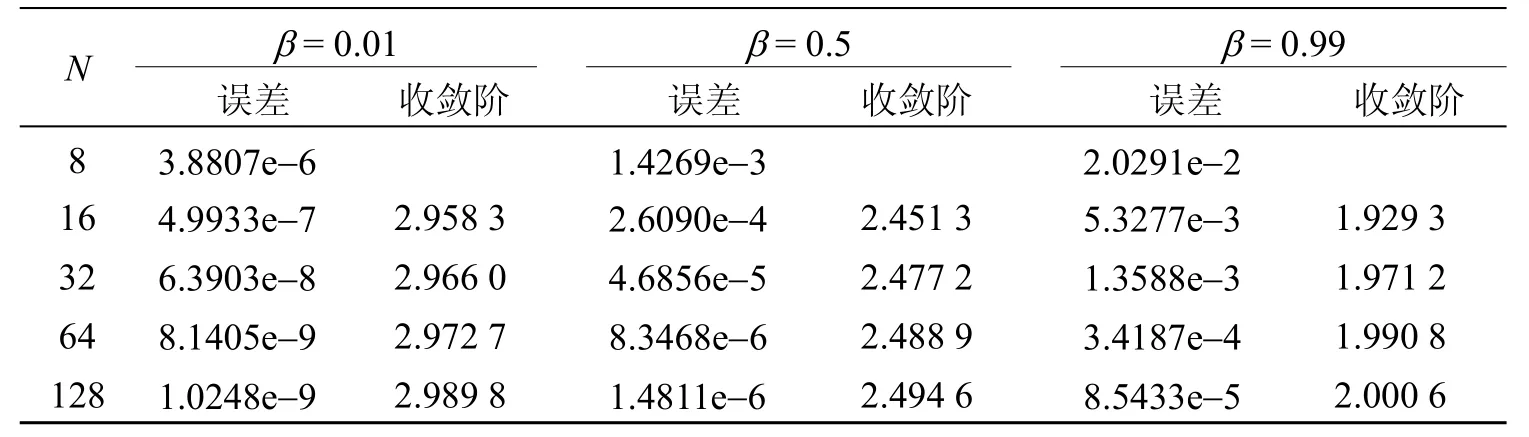
表2 例2 的数值结果
例1
例2
由表1、2 中的实验结果可知,数值格式(2)~(5)的收敛阶均达到了O(τ3-β),与定理2 中的理论结果相吻合。
3 结论
本文利用二次Lagrange 插值函数构造了Caputo 分数阶导数算子的一种数值离散方法,该方法的全局数值精度为O(τ3-β)。为了调查其实际使用效果,此数值方法被应用到了数值求解时间分数阶扩散方程当中,发现其数值效果与理论分析保持一致性。鉴于数值格式(2)~(5)的高精度性质,在其他类型的时间分数阶方程的数值模拟当中,该方法具有很好的应用潜力。

