基于模糊逻辑的电力系统动态稳定性分析
虞 婧 缪林鑫 李奕婵
(国网上海市电力公司经济技术研究院)
0 引言
同步发电机在电力系统中的稳定性会因转角的非周期性偏差或转速偏差的振荡而丧失。由于阻尼力矩的不足,这种振荡会维持和增长。电力系统稳定器产生一个正阻尼转矩,用于提高电力系统阻尼、解决低频振荡问题,是提高电力系统动态稳定性的重要措施之一。输入变量可以是转速、频率、功率等单变量,也可以是这些单变量的综合,简称PSS。大多数类型的PSS 是基于常参数线性模型的经典线性控制理论,但电力系统是非线性的,而低频振荡在电力系统中广泛存在,因此在许多文献中研究对这些器件调谐参数的优化技术。PSS 通过向系统输入新的状态变量来引入波动性,因此,本文使用比例、积分、微分相结合的PID 控制器,利用粒子群优化算法(PSO)在处理连续问题上的优势对PID 控制器进行智能优化。为实现快速响应,将模糊逻辑应用到PSO 中。
在单机无穷大系统中,采用基于模糊逻辑的粒子群算法优化PID 控制器代替传统的电力系统稳定器(PSS),通过粒子群优化和模糊逻辑对PID 控制器参数进行优化[1-3]。为了提高单机无穷大系统的动态稳定性能,以转子的转速变化量和加速度作为模糊逻辑粒子群优化PID 控制器的输入,对系统在不同扰动下的动态稳定性能进行了研究。将模糊逻辑粒子群优化PID 控制器的性能与基于教学优化、模糊教学优化、粒子群算法优化的PID 控制器以及常规电力系统稳定器PSS 的最优参数进行比较,结果表明,与其他控制器相比,模糊逻辑粒子群优化PID 控制器具有较小的期望偏差和较快的阻尼摆动来抑制低频振荡。
1 算法分析
比例、积分、微分相结合的PID 控制器由于其简单性和鲁棒性而得到了广泛的应用。通过控制理论和技术的发展,当今传统的PID 控制技术已经完全成熟,它具有算法简单、安装明显、设置舒适、应用专业性强等特点[4-5]。该控制器控制参数相互独立,参数的选定比较简单,通常固定不用经常改变。
在其他文献中,有学者提出了风力发电小频率震荡的联络线潮流控制。还有学者提出通过优化调速器PID 参数可以抑制可再生能源接入下电力系统的低频振荡。还有学者讨论了风电场在电网一体化过程中对改善频率控制的贡献。
模糊控制(FC)是一种智能控制方法,它首先将经验编成模糊规则,然后将来自传感器的实时信号模糊化,将模糊化后的信号输入,完成模糊推理,将推理后得到的输出量加到执行器上。关联输入和输出语言变量的隶属函数一般是在一个共同空间上预定义的。当不能清楚地识别明确的控制目标,或者控制目标是一个非常复杂的系统,难以得到其精确的数学模型时,模糊控制可以作为一种强有力的工具应用在电力系统中。
电力系统的结构是非线性的,在系统运行中如果发生任何突然的变化,电力系统就会失去其稳定性。电力系统的参数是随时间变化的,但是传统的电力系统稳定器的参数不会实时变化。因此本文采用基于模糊逻辑的粒子群算法优化PID 控制器。单机无穷大系统如图1 所示。为了提高系统的稳定性,将单机无穷大系统的转速变量Δω和加速度变量作为模糊逻辑粒子群优化PID 控制器的输入值。单机无穷大系统的线性模型主要用于研究电力系统的动态稳定性能,包括发电机转角与转速变化之间的机电转矩关系。
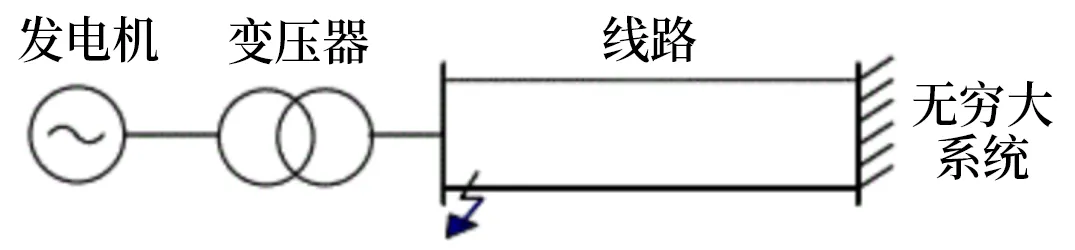
图1 单机无穷大系统
1.1 设备数学模型
用一阶传递函数可以给出风力发电机组(WTG)的基本模型如下:
式中,Kwtg为增益常数;Twtg为时间常数。
光伏机组(PV)是一种利用太阳能产生电能的电气设备。随着系统成本的降低,光伏技术有潜力成为未来电力供应的关键可再生能源之一。对于低频域分析,建立了光伏系统的传递函数模型如下:
式中,Tpv为PV 的时间常数。
1.2 控制理论模型
PID 二次控制器用于将互联区域之间的潮流保持在预定值,也用于控制同步发电机提供二次响应,二次响应总是发生在一次响应之后,并存在一定时间延迟。它被用于反馈传递路径以反应所测试系统保持稳定性的理想性能。
第i区域的PID 控制器的传递函数如下:
式中,Kpi,Kii,Kdi分别为比例素数,积分素数和导数素数;ui,ACEi为i区域的受控输出和跟踪误差信号。
粒子群优化(PSO)算法是假设在搜索区域中,有N个粒子,每个粒子代表一个解,对每个粒子搜索到最优解,目标函数的最优解则是群体搜索到最优解。在搜索区域的研究中,以Xi=(Xi1,...,Xim)来表示所代表的群体位置。用Vi=(Vi1,...,Vim)表示维度向量的群速度。第ith个粒子给出的最佳位置按粒子群前一个位置的Pi=(Pi1,...,Pim)和PG位置指数计算,然后PG成为全局最佳位置计算,粒子速度和新位置将用以下公式计算:
式中,C1和C2为加速因子的正常数;r为区间[0,1]中的随机值;参数W为提高粒子群算法整体性能的惯性因子。
1.3 采用粒子群优化算法(PSO)对PID 控制器整定
最终目标是优化PID 控制器并计算目标函数的最小值。目标函数可以最小化稳态误差Ess、超调Mp、上升时间tr和稳定时间ts,如下所示:
过程如下:
1)定义了粒子群算法的参数:迭代次数、群体规模、加速因子、惯性因子、位置矩阵Pi和速度矩阵Vi,以及KP、KI和KD的约束条件;
2)初始化每个粒子的值;
3)比较新旧粒子的位置,然后更新Pbest的最佳位置;
4)继续通过所有粒子搜索最佳Pbest,并将最佳位置表示为Gbest;
5)更新Vin和Pin;
6)更新PID 控制器参数。
1.4 自适应模糊PID 控制器原理
采用基于模糊逻辑的智能化PID 控制器是应对电力系统突发工况变化的实时快速动态响应方法。根据模糊逻辑粒子群优化PID 控制器设计原则,模糊控制器有两个输入,转速变化量Δω和加速度Δ,采用模糊化、模糊推理和去模糊控制器输出。参数GΔω和GΔω是驱动Δω和Δω进入模糊域的标度值,其中GKP、GKI、GKD是通过模糊方法计算出的驱动控制量进入控制对象域的值,作为Ku因子的区域Δω分别是[-Δωmax,Δωmax]和[-Δmax,Δmax],输出的区域是[-umax,umax]。式(6)中n和m是模糊域的最大输出值;l1,l2,l3是Ku的最大计算模糊值。
2 模糊规则设计
模糊规则是模糊控制器的核心,这个角色的目标是优化模糊逻辑粒子群优化PID 控制器的实时参数,模糊规则依赖于专家或工程师设计。传统的PID 控制器参数与特征曲线有关,PID 参数调整规则设置如下:
1)当PID 的输入Δω较大时,应减小输出期望偏差,尽快实现稳定,以提高系统的动态响应。因此必须选择较大的KP,并注意避免较大的Δω速率差饱和,采用较小的KD来避免较大的输出期望偏差,因此应采用KI=0。
2)在中等变化量的前提下,必须使GKP、GKI和GKD最小化,并取合适的值。
3)在系统是稳定的情况下,就意味着Δω和Δω很小,所以必须增加GKP和GKI,以提高系统的动态性能,进而避免稳态误差,所以GKD效应是非常必要的,一般而言,Δω可以放大GKD,也可以缩小GKD,与前面的调优步骤相关。
3 仿真及分析
本文采用三区域互联电力系统对随机负荷扰动进行研究。风力发电机组对电力系统动态稳定性存在影响,模糊逻辑算法可以将其影响考虑进测算过程中。在另一区域采用同样的三区互联系统作为测试系统,将风电机组接入系统中进行对比试验。对于所施加的负载扰动,分为测试有WTG 和无WTG 优化PID 控制器的动态性能。系统的动态响应如图2 所示。结果表明,带WTG 的PID 控制器在阻尼振荡、超调量和下调量方面性能稳定。仿真结果表明,WTG 可以作为频率的主要控制器。

图2 电力系统模型的动态响应分布
该控制器应用于单机无穷大系统,来提高电力系统动态稳定性能。以同步发电机转子的速度偏差Δω和加速度Δω为输入,代替传统的电力系统稳定器PSS。基于模糊逻辑的粒子群算法优化PID 控制器,每个输入设置多个模糊逻辑集。控制规则如下:x1=Ai1,x2=Ai2...xn=Ain,则y=Bi,该控制器输出到同步发电机励磁机来改变正阻尼值。采用粒子群优化算法的PID 控制器,根据最佳PID 参数和适应度函数得到图3 所示的算法的收敛特性。

图3 粒子群优化算法的PID 控制器收敛性
可以看到,基于粒子群优化算法的PID 控制器在到达一定迭代次数以后,目标函数的收敛性较好。
为了比较所提出的方法之间的潜在优点,将模糊逻辑粒子群优化PID 控制器的性能与基于教学优化、模糊教学优化、粒子群算法优化的PID 控制器以及常规电力系统稳定器PSS 的最优参数进行比较,在Matlab 软件中实现仿真。模拟研究对应于相同运行条件下,分别改变设备的运行状况进行仿真模拟,仿真如图4 所示。
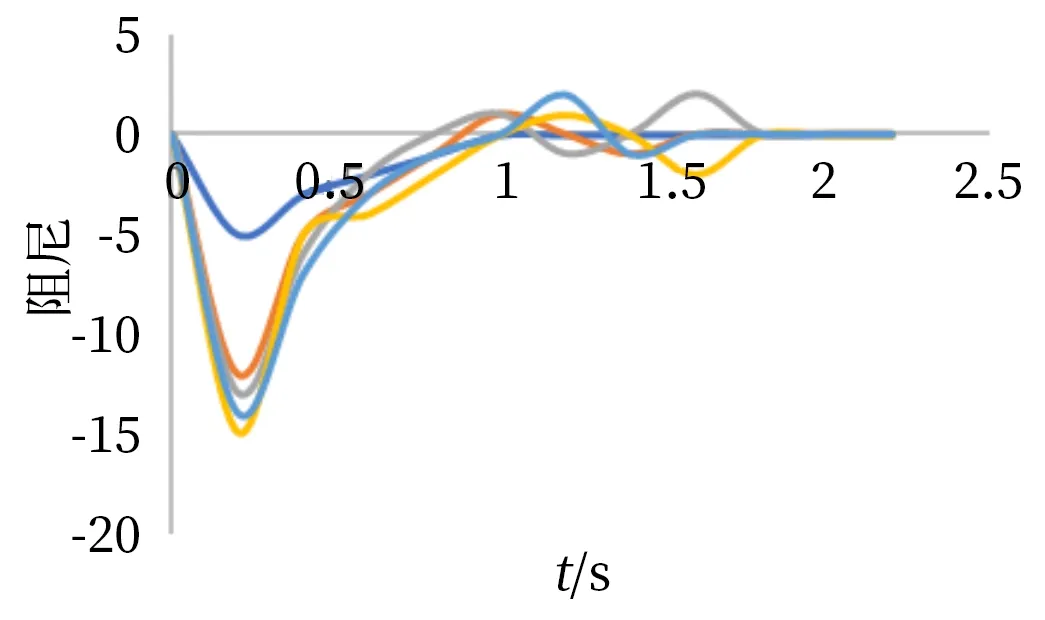
图4 不同控制器阻尼摆动曲线
仿真结果可以显示系统的动态响应效果,结果表明,与其他控制器相比,模糊逻辑粒子群优化PID 控制器具有较小的期望偏差和较快的阻尼摆动来抑制低频振荡。
4 结束语
电力系统的稳定性可能由于同步转矩的不足而受影响,也可能由于外部扰动引起的振荡而使阻尼转矩振荡不足而受限。本文采用粒子群优化模糊PID 控制器来提高单机无穷大系统的动态稳定性。采用粒子群优化算法和模糊控制器对PID 控制器参数进行优化设计,以转子的转速偏差Δω和加速度Δω作为模糊粒子群算法PID 控制器的输入值,对系统进行不同扰动下的检测。系统的动态性能表明,与其他控制器相比,模糊逻辑粒子群优化PID 控制器具有更好的性能。在今后的工作中,将尝试采用自适应TS 模糊控制器设计自适应PID 控制器,本文的研究为提高电力系统动态性能提供了参考依据。

