压力作用下KNbO3相变行为的分子动力学研究
张旭龙 曹玉莹 周 龙 马 治
(宁夏大学物理学院,宁夏 银川 750021)
0 引言
铁电材料由于具有优异的介电性、压电性、热释电性、铁电性且具有光电效应与声光效应,受到了广泛关注,并在铁电存储器、红外探测器及光学传感器等方面具有十分重要的应用。近年来,由于铁电材料存在极化强度与温度和电场的有效耦合,发现铁电材料在相变温度附近具有很大的电卡效应,铁电材料被认为是下一代固态制冷器件的理想选择。为了发展对环境友好且更加廉价高效的冷却技术,大量的电卡制冷器件应用研究已经被报道[1-2]。由于极化强度与应变梯度之间的耦合作用,发现铁电材料具有优良的挠曲电效应,并被广泛地应用于挠曲电能量采集器、挠曲电致动器、挠曲电传感器等电子器件上[3-5]。
铁电材料具有的一个重要特征就是相变点。在温度诱发极化相变中,将铁电相向顺电相转变的相变点也称为居里点。在居里点以下,材料为铁电体,展现出优异的铁电性,在居里点以上,材料为顺电体,不具有铁电性,极化强度为零。同时,由于铁电体的许多物理性质,如比热容[6]、极化强度[7]、介电常数[8]等,其在居里点附近会发生突变,在居里温度点所测量的值较大,偏离在其他温度下测量到的值。近年来,研究人员通过试验测量与理论计算积极探索铁电材料在高温或者高压下物理性质发生改变的规律,深入研究了许多铁电材料在温度或者压力作用下的相变行为。在铁电材料中,钙钛矿型铁电体是研究范围最广、研究热度最高的一类铁电材料,研究表明在高温或者高压下,钙钛矿型铁电体的对称性升高,结构变得更加规则,引起铁电体的自发极化减小,导致铁电性能降低,铁电材料最终变为顺电材料。
KNbO3作为典型的钙钛矿型铁电体,其在温度作用下的相变行为受到了广泛关注。Sepliarsky等[7]使用分子动力学模拟研究表明,其相变温度依次为225 K、475 K 和675 K。Hashimoto 等[8]使用分子动力学模拟研究表明其相变温度依次为325 K、525 K 和700 K。Golovina 等[9]通过试验研究表明其相变温度依次为263 K、498 K 和708 K。关于KNbO3在压力作用下的相变行为研究较少。另外,试验基本都是通过分析晶格参数来获得KNbO3的相变压力,很少通过分析其极化性能来获得相变压力。因此,本研究使用分子动力学方法对KNbO3铁电体在压力作用下的相变行为开展研究,通过分析铁电材料极化强度与晶格参数随压力的演变行为获得KNbO3铁电体的相变压力。同时,还研究了相变压力的尺寸效应和电场对相变压力的影响,这为铁电材料相变压力的调控起着较好的指导作用。
1 研究方法
分子动力学模拟被认为是研究许多离子系统结构和特性的有力工具,已经被广泛用来开展材料性能的研究。本研究基于Mitchell 和Fincham 提出的绝热核壳模型[10],使用LAMMPS 软件包对KNbO3开展分子动力学研究。在分子动力学研究中,绝热核壳模型不仅可以考虑离子极化,也可以考虑电子极化,所以它被广泛用于模拟BaTiO3、SrTiO3、PbTiO3、KNbO3、LiNbO3、KTaO3、Bi4Ti3O12等一系列钙钛矿型铁电材料。在核壳模型中,每一个原子都由一个带正电的核和一个带负电的壳组成,核和壳都带有部分电荷,核与壳的电荷之和就是每个原子的总离子电荷,核和壳的位置是以完全动态的方式确定的,其中核的质量占单个原子质量的90%,壳的质量占单个原子质量的10%[11]。
在KNbO3铁电体的模拟过程中,使用的相互作用势参数取自Sepliarsky 和Phillpot 等人开发的势函数[7],该势函数主要由两部分组成。第一部分是不同原子的壳与壳之间的相互作用,是通过Buckingham势描述的,见式(1)。
式中:r表示两个不同原子之间的距离;A、ρ和C是势函数的参数。第二部分是同一原子的核与壳之间的相互作用,是通过core-shell 势来描述的,见式(2)。
式中:r表示同一原子核壳之间的距离;k2和k4是势函数的参数。KNbO3铁电体使用的势函数见表1。

表1 KNbO3铁电体的势函数参数[12]
2 结果与分析
2.1 压力作用下的相变行为研究
为了研究KNbO3在压力作用下的相变行为,模拟中使用了三斜相(R3m)结构,构建了尺寸为10×10×10 的超胞(4.09 nm×4.09 nm×4.09 nm),总原子数为10 000。模拟设定时间步长为0.4 fs,使用周期性边界条件,在温度为250 K 的条件下,600 000步内将压力从0.000 1 GPa 升高到10 GPa。研究了KNbO3在三个方向上的极化强度及晶格参数随压力的演变行为,研究结果如图1所示。
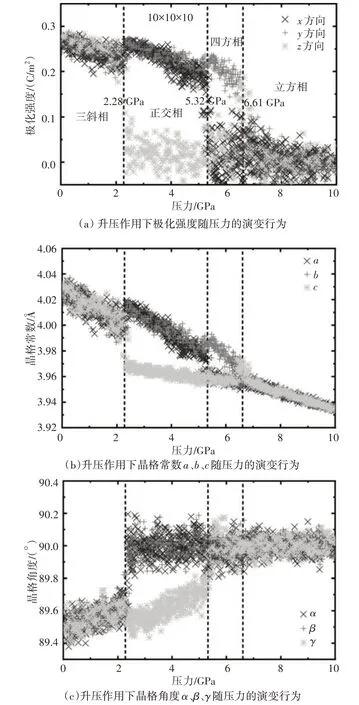
图1 升压作用下KNbO3的相变行为
如图1(a)所示,在压力作用下,KNbO3依次经历了铁电三斜相(R)→铁电正交相(O)→铁电四方相(T)→顺电立方相(C)的相变过程。在低压条件下,极化强度Px=Py=Pz≈0.28 C∕m2,KNbO3展现出的是铁电三斜相(R)。当压力升高到2.28 GPa 时,极化强度Px=Py≈0.28 C∕m2,Pz≈0 C∕m2,KNbO3表现出铁电三斜相(R)向铁电正交相(O)转变的相变行为。当压力升高到5.32 GPa 时,极化强度Py≈0.28 C∕m2,Px=Pz≈0 C∕m2,KNbO3表现出铁电正交相(O)向铁电四方相(T)转变的相变行为。当压力升高到6.61 GPa时,Px=Py=Pz≈0 C∕m2,KNbO3表现出铁电四方相(T)向顺电立方相(C)转变的相变行为。KNbO3铁电三斜相(R)的晶格常数a、b、c分别为4.09 Å、4.09 Å、4.09 Å,晶格角度α、β、γ分别为89.797°、89.797°、89.797°,顺电立方相(T)的晶格常数a、b、c分别为4.057 Å、4.057 Å、4.057 Å,晶格角度α、β、γ分别为90°、90°、90°。晶格常数a、b、c和晶格角度α、β、γ随压力的演变行为如图1(b)和图1(c)所示,研究表明在压力为0.000 1 GPa时,晶格常数和晶格角度的模拟结果与对应结构的参数比较吻合,在KNbO3晶格常数和晶格角度随压力的演变行为中仍然可以获得KNbO3的相变压力,依次为2.28 GPa、5.32 GPa和6.61 GPa。
另外,研究了KNbO3在压力作用下发生相变行为展现出的滞后现象。仍然使用上述研究中构建的模型,模拟条件保持不变,在600 000步内将压力从10 GPa降低到0.000 1 GPa,KNbO3在三个方向上的极化强度随压力的演变行为如图2所示。
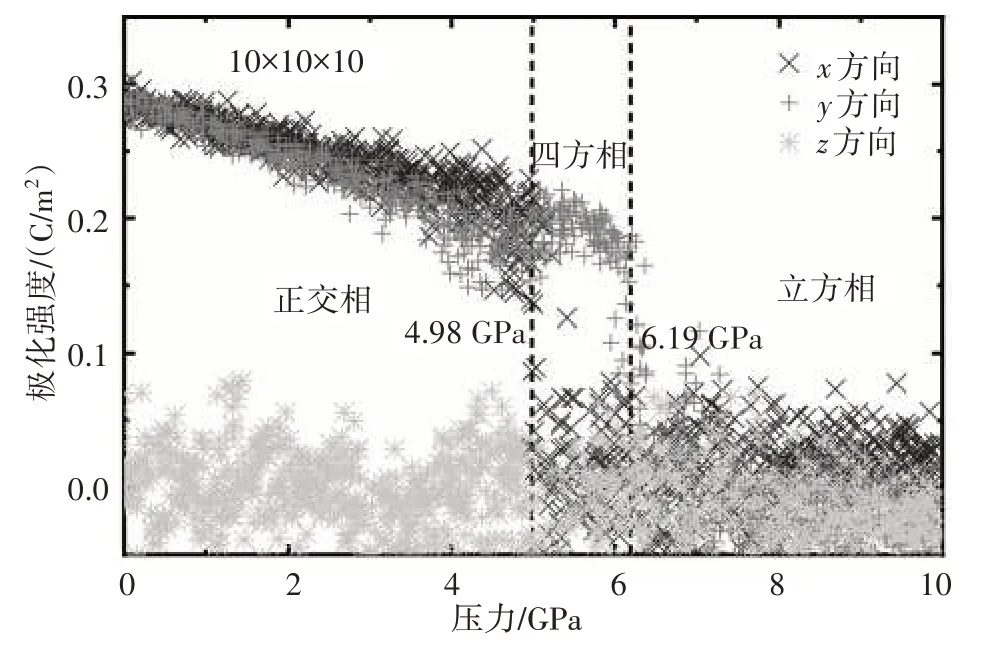
图2 降压作用下KNbO3的相变行为
如图2所示,研究发现在降压作用下,KNbO3依次经历了顺电立方相(C)→铁电四方相(T)→铁电正交相(O)的相变过程,其相变压力依次为6.19 GPa、4.98 GPa,相较于升压作用下获得的相变压力6.61 GPa、5.32 GPa 和2.28 GPa,在压力作用下相变行为仍然表现出滞后现象。其中将4.98~5.32 GPa 之间的区域称为铁电正交相(O)和铁电四方相(T)的两相共存区,将6.19~6.61 GPa 之间的区域称为铁电四方相(T)和顺电立方相(C)的两相共存区。
其他研究人员通过试验测量获得的相变压力见表2,将本研究模拟获得的相变压力与其他研究人员的试验结果进行比较。Shen 等[13]通过拉曼散射测量得出KNbO3的三个相变压力依次为2 GPa、6 GPa 和9 GPa。Chervin 等[14]在温度为300 K 的条件下研究了KNbO3的相变行为,研究表明KNbO3从铁电正交相(O)到铁电四方相(T)的相变行为发生在4~5 GPa,铁电四方相(T)到顺电立方相(C)的相变行为发生在9 GPa。Shamim 和Ishidate[15]通过拉曼散射研究了KNbO3的相变行为,表明KNbO3从铁电正交相(O)到铁电四方相(T)及进一步到顺电立方相(C)的相变行为依次发生在7 GPa、8 GPa。KNbO3相变压力的模拟结果与其他研究人员的试验结果之间存在一定的差异,产生这些差异的原因可能主要是测量条件及模拟过程中一些参数的设置不同,如温度、升压速率等。另外,尺寸效应也是影响相变压力的一个主要因素[16-17]。
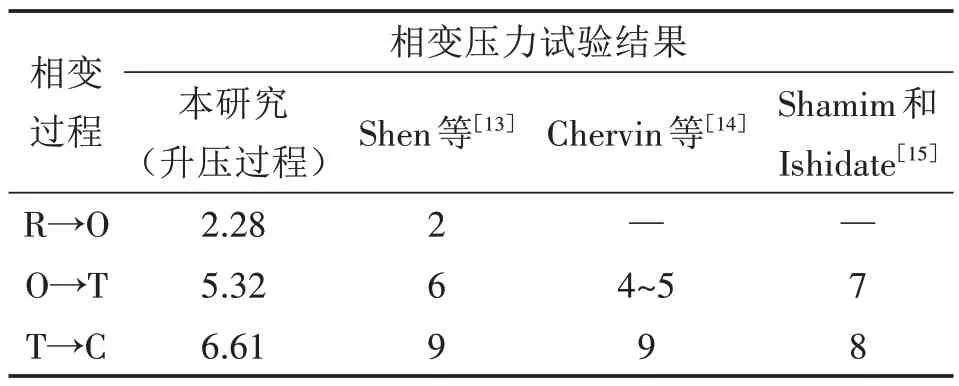
表2 KNbO3相变压力比较单位:GPa
2.2 相变压力的尺寸效应
为了进一步分析样品尺寸大小对KNbO3相变压力的影响,在模拟中仍然使用了三斜相(R3m)结构,构建了尺寸依次为8×8×8(3.272 nm×3.272 nm×3.272 nm)、10×10×10(4.09 nm×4.09 nm×4.09 nm)、12×12×12(4.908 nm×4.908 nm×4.908 nm)、14×14×14(5.726 nm×5.726 nm×5.726 nm)、16×16×16(6.544 nm×6.544 nm×6.544 nm)和18×18×18(7.362 nm × 7.362 nm × 7.362 nm)的超胞,总原子数依次为5 120、10 000、17 280、27 440、40 960 和58 320,分别研究了不同模型在压力作用下的相变行为。模拟中仍然设定时间步长为0.4 fs,使用周期性边界条件,温度为250 K 的条件下,在600 000 步内将压力从0.000 1 GPa 升高到10 GPa。所有尺寸下样品的研究结果如图3所示。
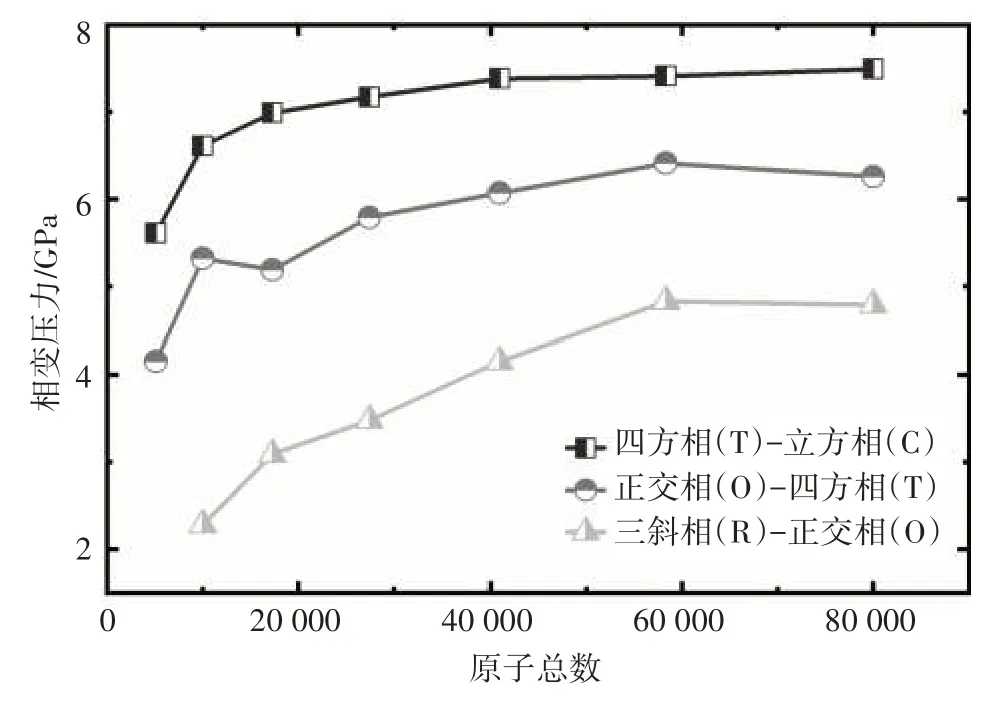
图3 相变压力的尺寸效应
不同尺寸KNbO3的相变压力点如图3 所示,研究表明KNbO3的相变压力具有非常显著的尺寸效应。当体系的原子总数小于30 000时,三个相变压力点随着原子数目的增多变化很大;当体系的原子总数超过30 000 时,铁电正交相(O)向铁电四方相(T)和铁电四方相(T)向顺电立方相(C)转变的相变压力保持稳定;而只有当体系的原子总数超过60 000 时,铁电三斜相(R)向铁电正交相(O)转变的相变压力才会保持稳定。因此,只有当KNbO3体系的原子总数超过60 000时,才能获得稳定的相变压力。另外,研究表明,当KNbO3的原子总数大于10 000 时,从铁电三斜相(R)到铁电正交相(O)的相变压力在2.28~4.83 GPa之间,从铁电正交相(O)到铁电四方相(T)的相变压力在5.32~6.41 GPa 之间,这与Shen等[13]的试验结果比较接近。从铁电四方相(T)到顺电立方相(C)的相变压力在6.61~7.41 GPa之间,这与Shamim 和Ishidate[15]的试验结果比较接近。
2.3 电场对相变压力的影响
进一步研究了电场的大小和方向对相变压力的影响,在模拟中仍然使用了三斜相(R3m)结构,构建了尺寸为10×10×10(4.09 nm×4.09 nm×4.09 nm)的超胞,总原子数为10 000。模拟中设定时间步长为0.4 fs,使用周期性边界条件,在温度为250 K 的条件下,在600 000 步内将压力从0.000 1 GPa 升高到10 GPa。同时分别在[001]、[110]和[111]方向上施加恒定电场,对应的电场分别设置为[0,0,E]、[E,E,0]和[E,E,E]的形式,研究了电场大小和方向对相变压力的影响,研究结果如图4所示。
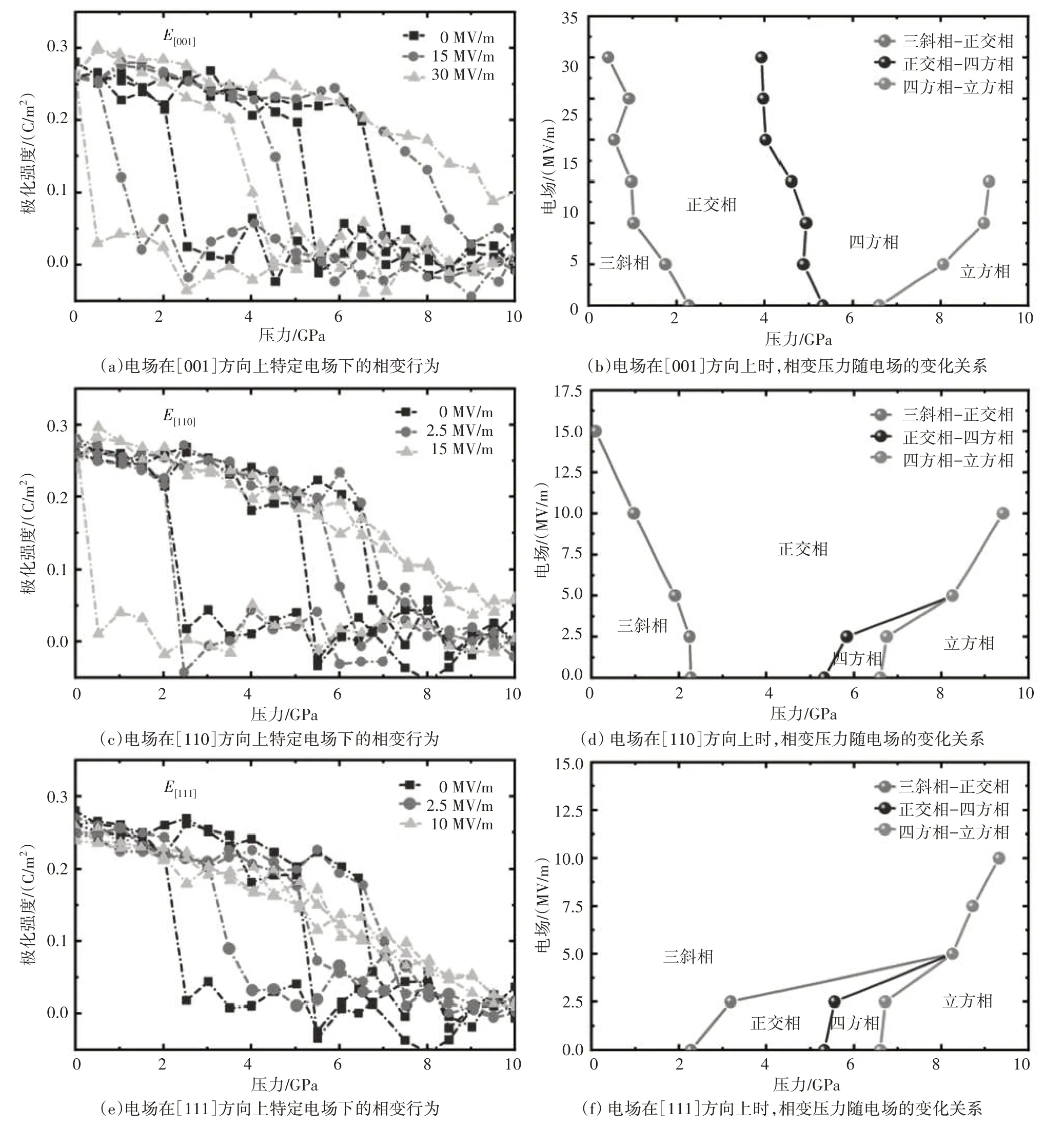
图4 电场—压力相图
KNbO3在特定电场下的相变行为如图4(a)、4(c)、4(e)所示,研究表明在不同电场下,相变压力会向更高或更低的压力偏移。为了清楚地描述相变压力随电场的变化情况,在[001]、[110]和[111]方向上施加电场时,相变压力随电场大小变化的关系如图4(b)、4(d)、4(f)所示。如图4(b)所示,当在[001]方向上施加电场,电场大小从0 MV∕m 升高到30 MV∕m时,铁电三斜相(R)向铁电正交相(O)转变的相变压力和铁电正交相(O)向铁电四方相(T)转变的相变压力都随着电场的增大而减小,铁电三斜相(R)和铁电正交相(O)消失的最强电场远高于在模拟过程中施加的最高电场,最后只有铁电四方相(T)存在。如图4(d)所示,当在[110]方向上施加电场,电场大小从0 MV∕m 升高到15 MV∕m 时,铁电三斜相(R)向铁电正交相(O)转变的相变压力随着电场的增大而减小;当电场大小为15 MV∕m 时,铁电三斜相(R)消失,铁电正交相(O)到铁电四方相(T)转变的相变压力随着电场的增大而增大;当电场大小为5 MV∕m 时,铁电四方相(T)消失,这个现象在电场—压力相图中可以被预测到,最后只有铁电正交相(O)存在。如图4(f)所示,当在[111]方向上施加电场,电场大小从0 MV∕m升高到10 MV∕m时,铁电三斜相(R)向铁电正交相(O)转变的相变压力和铁电正交相(O)向铁电四方相(T)转变的相变压力都随着电场的增大而增大。当电场增加到5 MV∕m 时,铁电正交相(O)与铁电四方相(T)都消失,这个现象在电场—压力相图中也可以被预测到,最后只有铁电三斜相(R)存在。
3 结语
本研究利用分子动力学模拟来研究KNbO3在压力作用下的相变行为。通过分析极化强度和晶格参数随压力的演变行为获得KNbO3的相变压力依次为2.28 GPa、5.32 GPa、6.61 GPa;同时发现KNbO3在压力作用下的相变行为也存在滞后现象。研究表明,铁电正交相(O)和铁电四方相(T)的两相共存区的压力区间为4.98~5.32 GPa,铁电四方相(T)和顺电立方相(C)的两相共存区的压力区间为6.19~6.61 GPa。研究了KNbO3相变压力的尺寸效应,只有当原子数超过60 000 时,才能获得宏观上稳定的相变压力。分析了电场对相变压力的影响,电场的大小和方向对相变压力都有显著的影响,在电场的作用下,相变压力会向更高或者更低的压力点偏移,这为调控KNbO3的结构和性能提供了有意义的指导。

