基于群组结构算法的贵州省粮食产量影响因素分析

李东升 邱宇婷 潘春燕

（1.黔南民族师范学院数学与统计学院，贵州 都匀 558000；2.湖南师范大学附属湘才学校，贵州 都匀 558000）

0 引言

贵州省作为我国农业大省，粮食产量一直是该省经济发展的重要指标之一。贵州省的地理环境和气候条件具有特殊性，影响粮食产量的因素也比较复杂，要进行深入分析和研究。在此背景下，基于群组结构算法成为一种有效的方法，能更好地预测出影响贵州省粮食产量的因素。

群组结构算法是一种基于数据的分析方法，通过将数据划分为不同群组，可揭示数据间的内在联系和规律。在对粮食产量影响因素的研究中，可对相关数据进行分类，如自然因素、社会因素、科技因素等［1-10］，利用群组结构算法对其进行分析，找出数据间的关系和影响因素。通过这种方法能更好地了解贵州省粮食产量的变化趋势，并预测出可能的影响因素，从而为贵州省农业生产提供科学依据和决策支持。

本研究将探讨群组结构算法在贵州省粮食产量影响因素分析中的应用，为贵州省农业生产提供有益的参考和借鉴，同时为群组结构算法在农业领域中的应用提供实践经验。

1 算法原理

考虑自变量具有n×p维的线性回归模型，自变量可分为J个不重叠的组结构，具体组结构模型见式（1）。

式中：y为n×1 的向量；Xj为n×dj的矩阵；dj为自变量的j个组；回归系数βj=（βj1，…，βjdj）为dj×1 的向量，表示第j组的回归系数；ε为随机误差向量。

组结构中的惩罚函数是通过约束模型的整组参数βj来获得最小化损失函数的，得到模型参数的估计值，并选择重要的组变量。目标函数一般形式见式（2）。

式中：L（β|y,X）为损失函数，不同模型的损失函数是不同的，本研究选取的损失函数为L（β|y,X）=||y-Xβ||2；Pλ（|β|）为参数的惩罚函数，通常单个变量的惩罚函数为Lq范数，即为调整参数，选择合适的λ值，可得到最优解。

1.1 L2 Group MCP

2011 年，Ma 等［11］提出L2Group MCP（grMCP），其惩罚估计见式（3）。

1.2 CMCP

2009 年，Breheny 等［12］提出composite MCP（CMCP），其惩罚估计见式（3）。

1.3 Lasso

1996 年，Tibshirani［13］提出Least Absolute Shrinkage and Selection Operator（Lasso），其惩罚估计函数见式（5）。

式中：λ为调整参数，其决定了对参数估计的压缩力度，令当λλ0时，Lasso 会将原始最小二乘法估计向零压缩，部分系数可能会刚好压缩到0；当时，通过Lasso方法选择的变量个数将近似等于全模型中变量个数的一半。

2 实证分析

粮食安全事关国家安全和发展大局，不能有丝毫的忽视和放松，而粮食产量受到多个因素的影响，如自然因素、科技因素、社会因素等。为探究影响贵州省粮食产量的主要因素，使用上述方法来探寻影响粮食产量的因素，并基于2000—2021 年贵州省与粮食产量相关的数据（数据来自贵州省统计局），以粮食产量为因变量，从自然因素、科技因素、社会因素中选取16 个指标来研究贵州省粮食产量的影响因素，具体指标见表1。

表1 变量符号定义

其中，自然因素包括有效灌溉面积、粮食作物播种面积和农作物受灾面积，科技因素包括农业机械总动力、化肥施用量、农用薄膜使用量和农药使用量，社会因素包括农业生产支出、复种指数、耕地产出率、农村全社会用电量、农村劳动力、农业生产资料价格指数、农村常住人口数、农村居民人均消费性支出和农业生产用水量。

为探究影响粮食产量的因素，本研究采用群组Lasso（Group Lasso，grLasso）、群组MCP（Group MCP，grMCP）、复合MCP（cMCP）、群组SCAD（Group SCAD，grSCAD）、Lasso、MCP 和SCAD 等分别建模，并使用模型拟合优度R2对模型进行评价。R2值越接近1，表明模型的拟合优度越好。

在建模前，使用R 语言MissForest 包中的miss-Forest 函数对数据缺失值进行补充，missForest 函数是一种性价比较高的缺失值补充方法，能同时对连续变量和离散变量进行填补。在将缺失值填补完整后，为检验数据规范化是否会影响数据建模效果，先不对数据进行归一化处理，直接对其进行建模，具体归回系数和模型的拟合优度R2见表2。

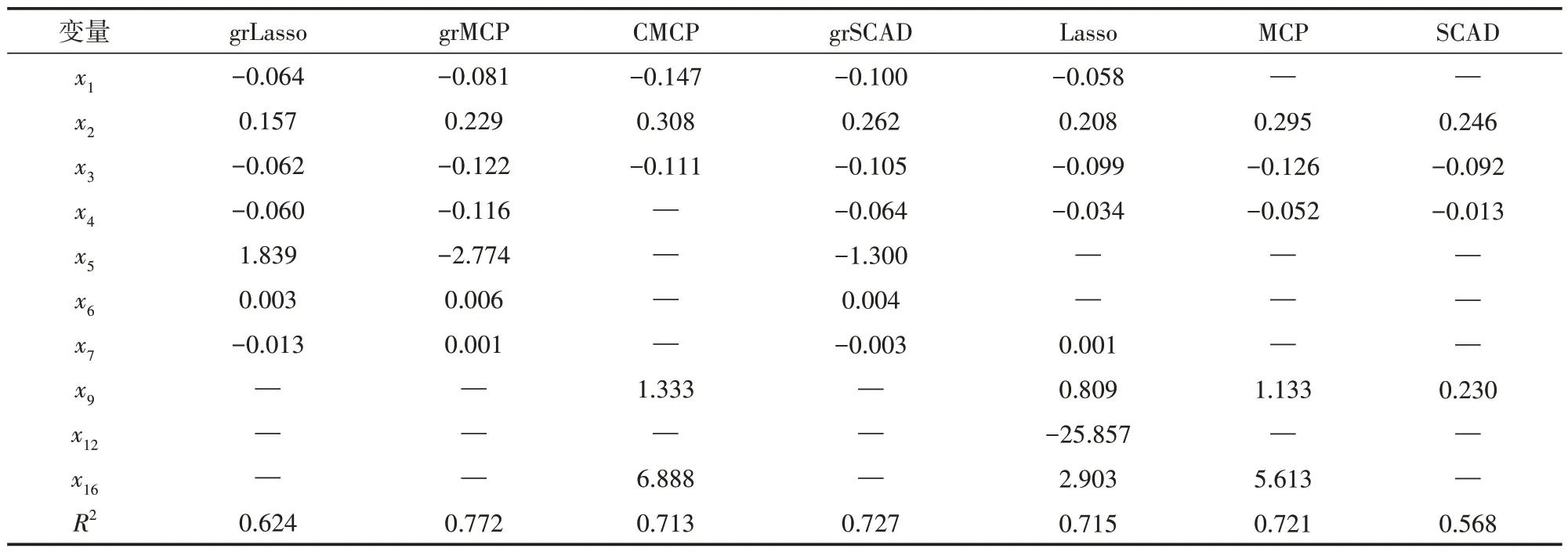
表2 未归一化处理的多种模型回归系数及模型拟合优度结果

由表2 可知，从16 个指标中选出10 个指标作为影响粮食产量的因素，由不同模型的拟合优度R2值可知，采用grMCP 法构建的模型是最优的，该模型的拟合优度为0.772。由该模型可知，影响粮食产量的主要因素包括有效灌溉面积（x1）、粮食作物播种面积（x2）、农作物受灾面积（x3）、农业机械总动力（x4）、化肥施用量（x5）、农用薄膜使用量（x6）和农药使用量（x7）。

由于指标的量纲不统一，要对数据进行归一化处理，具体结果见表3。

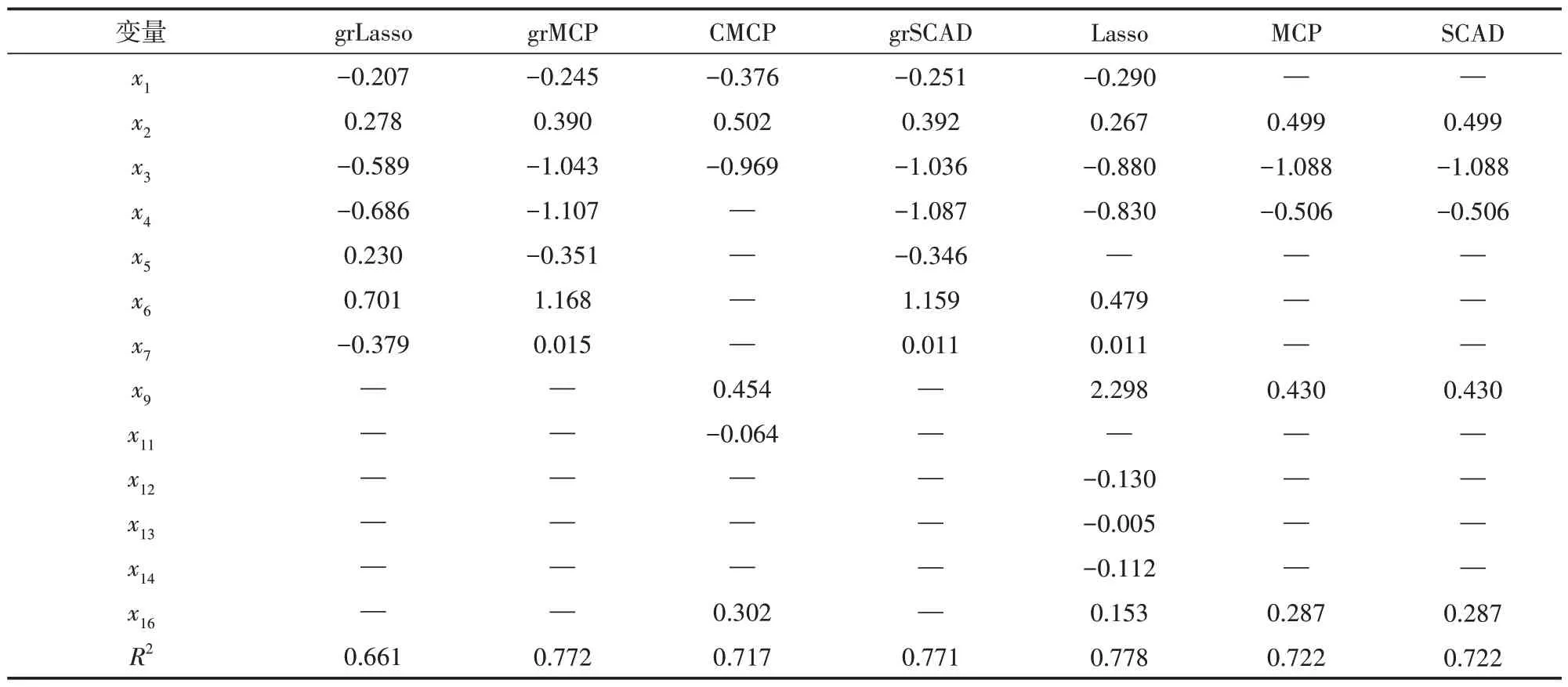
表3 归一化处理的多种模型回归系数及模型拟合优度结果

由表3 可知，从16 个指标中选取13 个指标作为粮食产量的影响因素。由不同模型的拟合优度R2可知，对数据进行归一化处理后，所有模型的拟合优度R2都出现小幅度上涨，表明对数据进行归一化处理是必要的。相比其他方法，使用Lasso 法和grMCP 法构建的模型是最优的，二者的拟合优度分别为0.778 和0.772。由Lasso 模型可知，影响粮食产量的因素分别为有效灌溉面积（x1）、粮食作物播种面积（x2）、农作物受灾面积（x3）、农业机械总动力（x4）、农用薄膜使用量（x6）、农药使用量（x7）、复种指数（x9）、农村劳动力（x12）、农业生产资料价格指数（x13）、农村常住人口数（x14）和农业生产用水量（x16）；由grMCP 模型可知，影响粮食产量的因素分别为有效灌溉面积（x1）、粮食作物播种面积（x2）、农作物受灾面积（x3）、农业机械总动力（x4）、化肥施用量（x5）、农用薄膜使用量（x6）和农药使用量（x7）。从所有模型来看，粮食作物播种面积（x2）和农作物受灾面积（x3）为影响粮食产量的主要因素。

3 结语

在实际生产中，变量为群组结构，如粮食产量主要受自然因素、科技因素和社会因素的影响，而这3 个维度的因素又包含16 个指标。在这种情况下，使用单变量选择方法会忽略分组信息，从而导致变量选择效果大大降低。因此，本研究采用群组MCP（grMCP）、复合MCP（cMCP）和Lasso 等方法，对影响贵州省粮食产量的因素进行建模分析。通过对7 种方法的对比可知，有效灌溉面积（x1）、粮食作物播种面积（x2）、农作物受灾面积（x3）、农业机械总动力（x4）、农用薄膜使用量（x6）和农药使用量（x7）等因素是影响贵州省粮食产量的主要因素。