唐山紫荆学校隔震结构分析与设计
刘 华, 史炎升, 卢清刚, 苗启松, 王俊亮
(北京市建筑设计研究院有限公司,北京 100045)
0 引言
随着国家经济的发展和对建筑物抗震要求的逐步提高,隔震作为一种能从根源上“隔离”地震的工程技术,以其简明的力学原理和显著的减震效果而得到了广泛发展应用,如北京大兴机场航站楼[1]、海口美兰机场航站楼[2]等。
唐山紫荆学校位于河北省唐山市,属于高烈度地区的学校建筑,采用隔震技术,设计完成于2021年8月,处于《建筑隔震设计标准》(GB/T 51408—2021)[3](简称隔标)发布但尚未实施阶段,工程以《建筑抗震设计规范》(GB 50011—2010)(2016年版)[4](简称抗规)为主要设计依据。本文以唐山紫荆学校实际工程项目为例,针对两本设计规范形成的三种设计方法进行了对比分析。
许多学者对于隔震设计中的计算方法、参数取值、体系对比等方面做了大量研究,如修明慧等[5]提出了隔标中的直接分析方法;孙海宁[6]对比了RC框架和剪力墙结构分别按抗规和隔标设计的差异;刘立德等[7]研究了RC框架-核心筒体系基于抗规和隔标的设计方法对比,周颖等[8]研究了基于位移-速度-加速度三联反应谱的隔震结构整体设计法。而在工程设计过程中存在的楼梯穿隔震层、局部大跨度结构隔震等细节问题目前还罕有论述。本文将以设计要点的形式,对一些关键问题进行总结归纳。
1 工程概况
本工程为唐山紫荆学校I段教学楼,地上采用钢筋混凝土框架-剪力墙体系。根据《唐山市防震减灾条例》[9]规定,教学楼抗震设防烈度由8度(0.2g)提高至9度(0.4g),场地类别Ⅱ类,设计地震分组第二组,场地特征周期Tg=0.40s,多遇地震水平影响系数最大值0.32。建筑地上4层,总高度21.6m,平面最小宽度129m,高宽比0.17<4.0。结构模型如图1所示。

图1 结构模型
1.1 设计条件
采用基础隔震技术进行计算分析,隔震支座选用天然橡胶支座和铅芯橡胶支座,本工程所用隔震支座参数见表1。采用ETABS19软件进行结构分析。本工程隔震层分别落在人防地下室顶、普通地下室顶和无地下室部分基础顶,隔震支座布置条件复杂,结构整体剖面如图2所示。
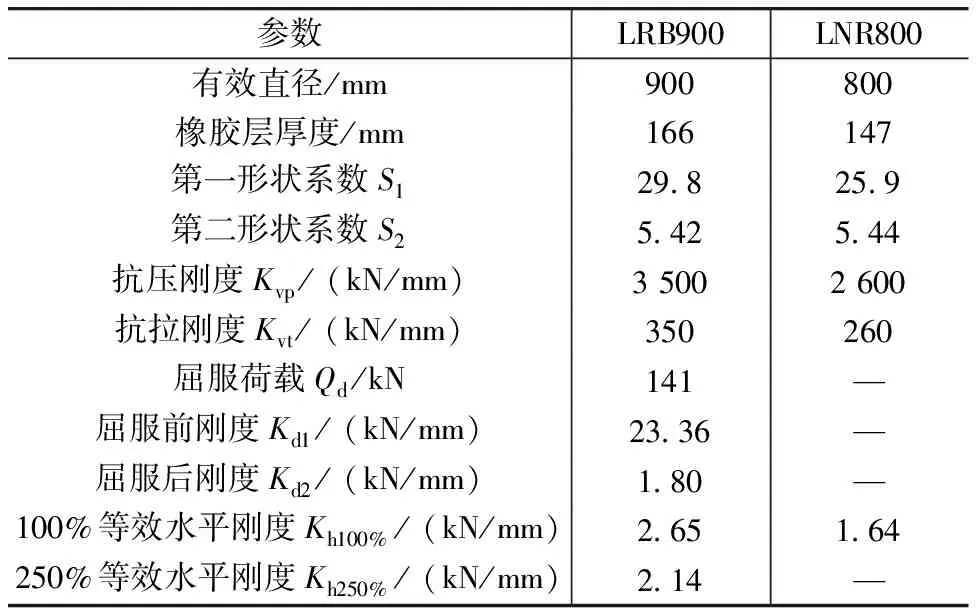
表1 隔震支座参数
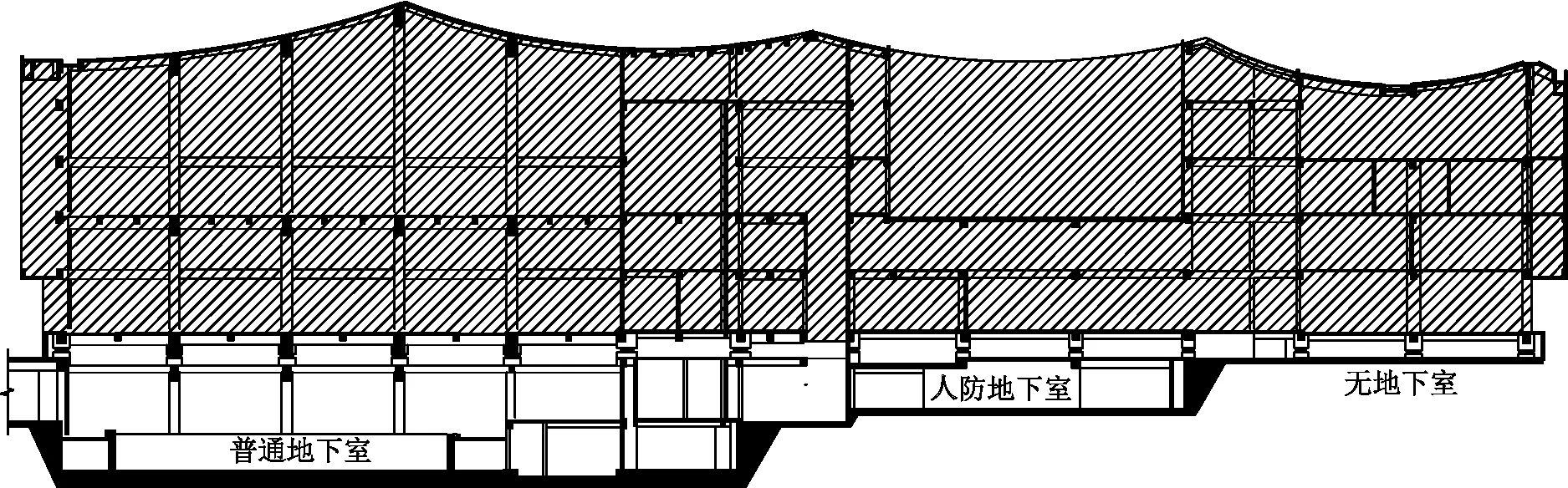
图2 结构剖面图
为了使隔震层具有足够的抗扭刚度,铅芯橡胶支座LRB沿建筑物外围布置,建筑内部布置普通橡胶支座LNR,如图3所示。经过计算,支座面压均满足抗规和隔标要求。
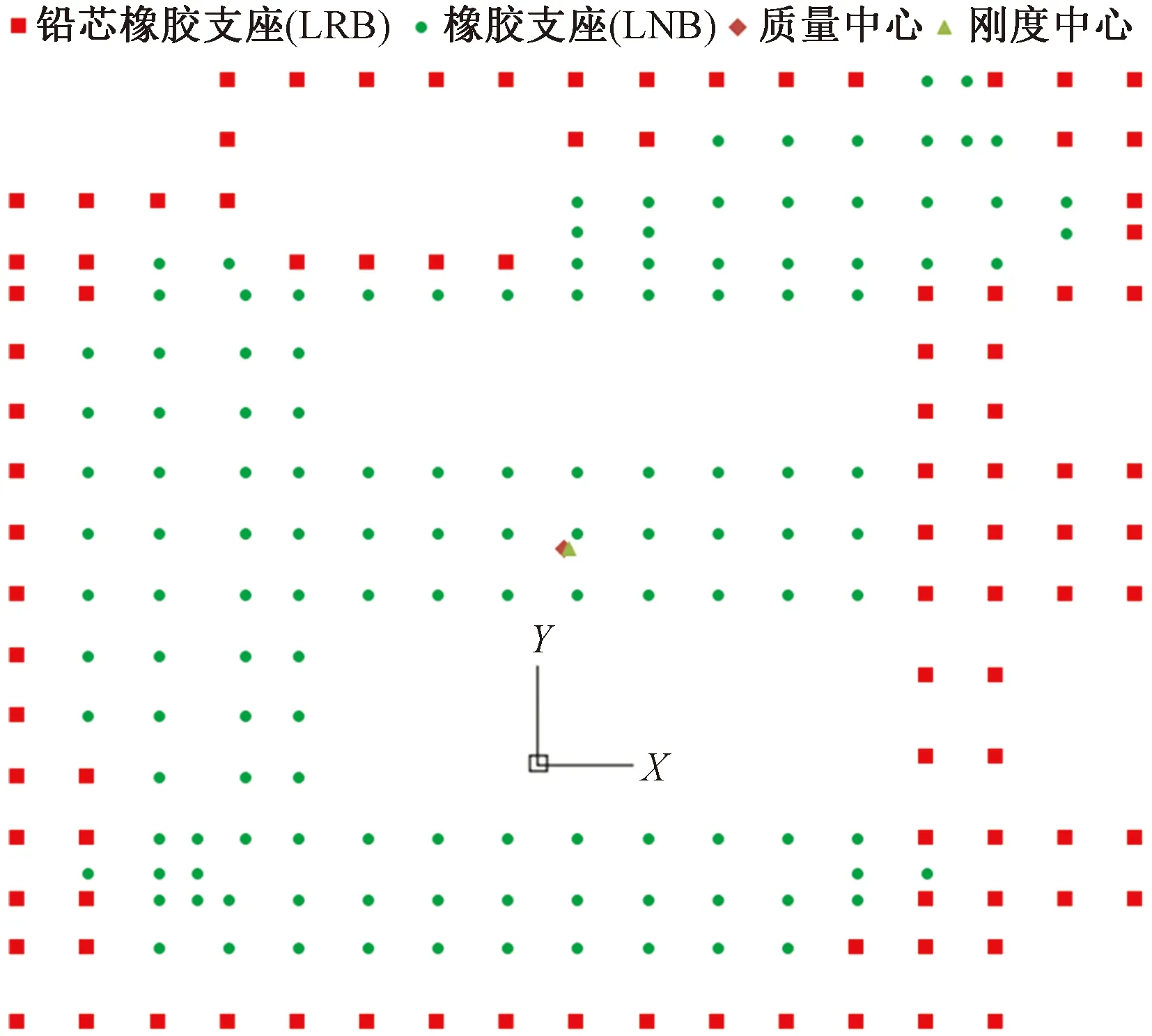
图3 隔震支座布置图
根据抗规要求,隔震结构采用减震系数法进行设计,采用时程分析法计算非隔震模型与隔震模型的各层最大剪力比,得到整体减震系数为0.299,满足降一度要求。用于设计的柱底铰接非隔震模型按照8度(0.2g)多遇地震输入地震作用。根据隔标要求,当采用振型分解反应谱法时,应将下部结构、隔震层及上部结构进行整体分析。在基础顶和地下室柱顶设置隔震支座,用于计算和设计的带隔震支座的整体隔震模型按照9度(0.4g)设防地震输入地震作用。
在实际工程中,形成了一种介于抗规和隔标之间的设计方法,采用带隔震支座的整体隔震模型计算分析,地震作用按照9度(0.4g)多遇地震输入地震作用。三种设计方法的特点如表2所示。
1.2 模型准备
对于常规的非隔震结构,自振周期为结构固有的动力特性,当按弹性设计时,多遇、设防、罕遇地震下的结构周期均为定值。但是对于隔震结构,由于隔震橡胶支座的非线性行为,在不同地震下的变形、刚度会有区别。
抗规中隔震支座的刚度按照设防地震100%、罕遇地震250%剪切应变的等效刚度取值。对于抗规两段式减震系数设计方法考虑支座剪切性能偏差调整系数,此等效刚度可以保证一定的安全度。但是对于隔标要求的整体计算模型,结构在设防地震下,隔震支座不一定能达到100%剪切变形,由此造成的刚度和阻尼比误差,将对结构整体动力特性造成较大影响,难以准确计算地震作用。因此,在整体计算模型中应采取迭代方式[10]确定不同地震烈度下的隔震支座等效刚度、等效阻尼比和自振周期。迭代流程如图4所示。主要关键步骤为:1)假定初始隔震层位移,计算支座水平等效刚度;2)假定隔震支座阻尼比,形成隔震层阻尼比;3)迭代计算实际隔震层位移和模型阻尼比;4)迭代误差小于一定范围则认为等效刚度和等效阻尼比符合实际受力情况。

图4 支座参数迭代流程
本工程用于抗规和隔标的整体分析法两种计算模型,分别按照9度多遇和设防地震进行支座等效线性化参数迭代,得到模型动力特性及支座参数如表3所示。
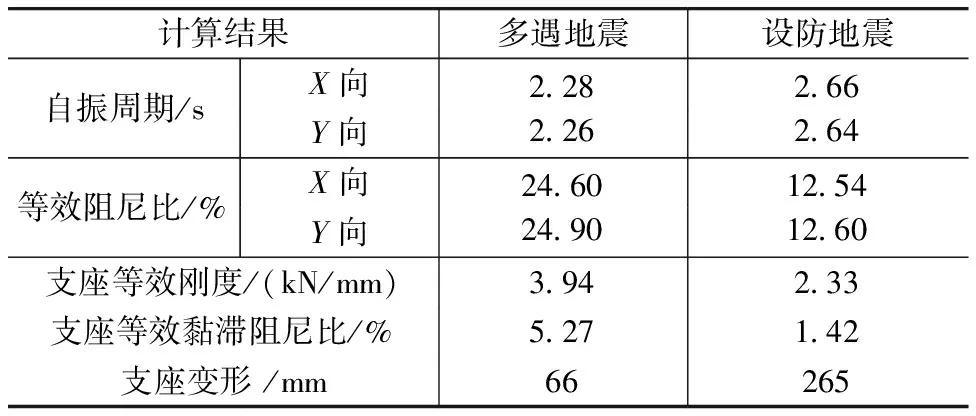
表3 整体分析模型参数
可见对于整体分析的隔震模型,不同地震烈度下的模型参数会有较大差别,采用振型分解反应谱(QC)法计算地震作用时,周期、阻尼比的差异对于地震影响系数的取值会有极大影响。本工程按带支座整体模型等效线性化迭代计算后显示,多遇地震下支座实际剪切应变为39%,设防地震下支座实际剪切应变为159%,与抗规假设的100%剪切应变均有较大差异。因此对于整体分析模型,进行等效线性化迭代十分必要。
采用抗规减震系数设计方法的计算模型为不带隔震支座的柱底铰接模型,模型参数相对简明,此处不再赘述。
1.3 结果对比分析
(1)三种设计方法采用的计算模型动力特性参数如表4所示。与非隔震模型相比,小震隔震模型周期延长约3.12倍,中震隔震模型周期延长约3.64倍。对于减震系数法的非隔震模型可直接采用CQC法进行求解,而对于隔标整体模型,由于隔震支座非比例高阻尼的存在,需采用复振型分解反应谱(CCQC)法进行求解。
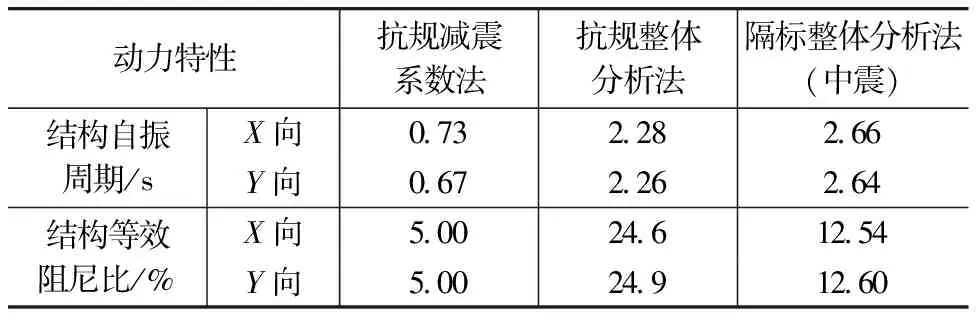
表4 动力特性对比
(2)本工程平面刚度、质量分布均匀,X、Y向结构指标接近。以X向为例,提取三种计算方法得到的X向地震楼层剪力对比,如表5所示。
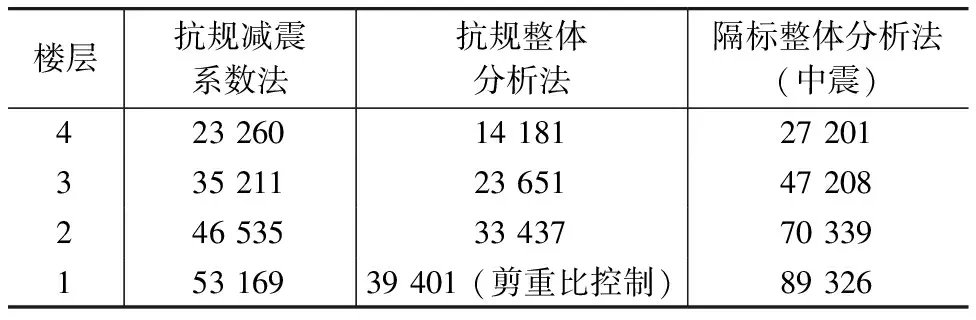
表5 X向地震楼层剪力对比/kN
采用抗规整体分析法计算的楼层剪力值最小,基底剪力约为减震系数法的74%,且由最小剪重比控制,说明采用该设计方法时,减震效果已超过1度,单从基底剪力角度分析,减震效果约为1度半,即从9度(0.4g)降至7度(0.15g)。由于采用设防地震计算并设计,采用隔标计算的基底剪力约为减震系数法的1.6倍,对于上部结构的影响大致为7度(0.1g)设防地震水平。值得注意的是,采用隔标计算得到的隔震层以上地震剪力衰减迅速(图5),说明采用该方法计算的各楼层地震作用沿高度分布更接近于矩形,而不是抗震结构的倒三角形,符合隔震结构地震作用分布规律[7]。
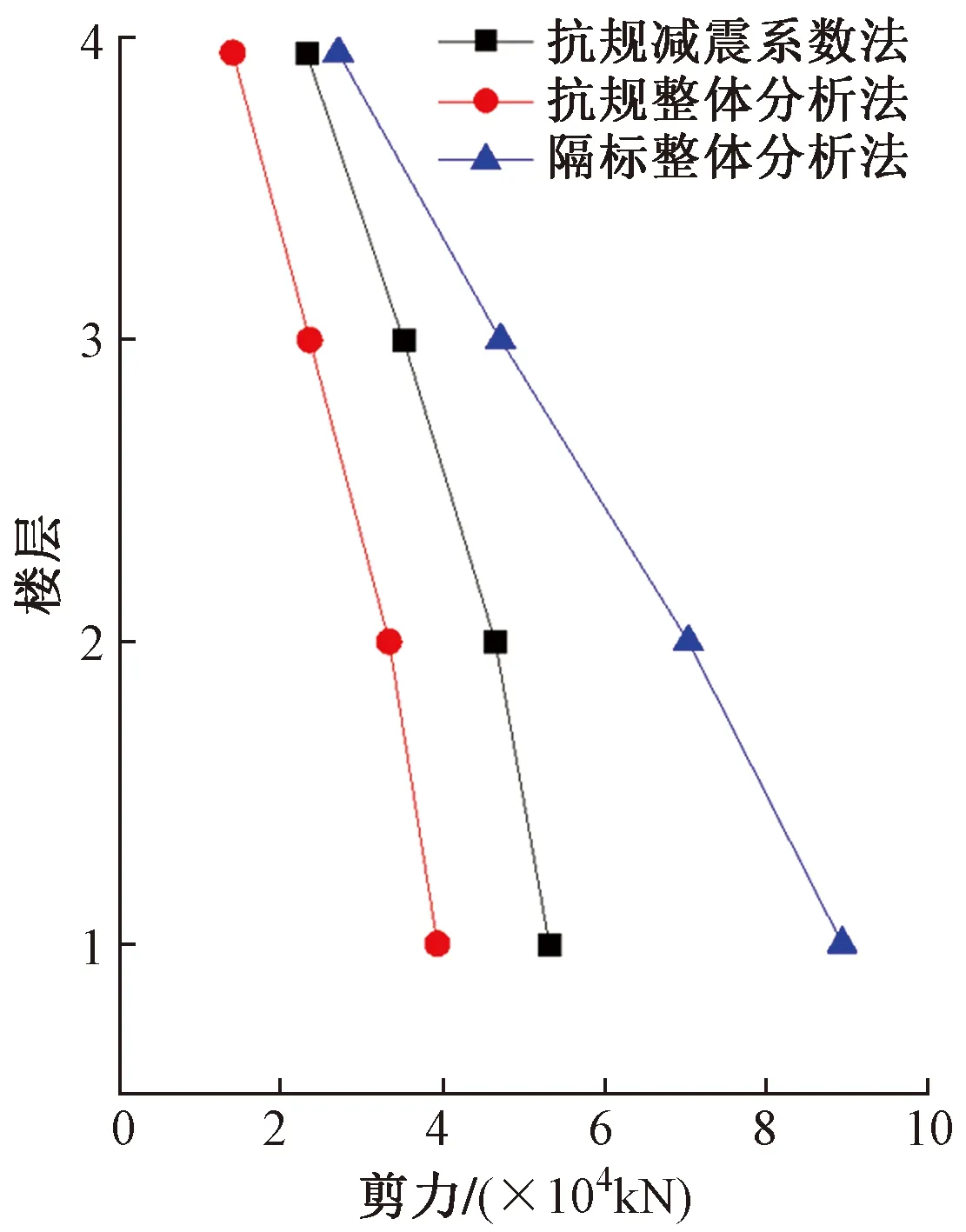
图5 X向地震楼层剪力分布
(3)本工程按三种计算方法得到的层间位移角数据如表6、图6所示。按抗规多遇地震和隔标设防地震设计的框架-剪力墙结构层间位移角限值分别为1/800和1/500。
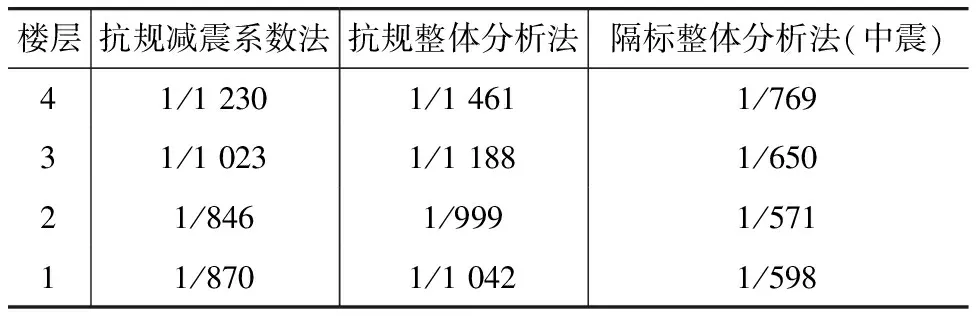
表6 X向地震层间位移角对比
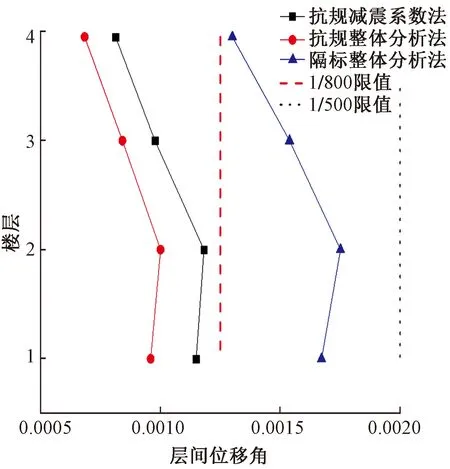
图6 X向地震层间位移角分布
(4)本工程采用隔震支座最小直径为800mm,橡胶层总厚度最小值为147mm,因此最大位移限值为Max(0.55D,3Tr)=440mm,D为隔震支座有效直径,Tr为隔震支座橡胶层厚度。隔震沟按照最大位移的1.2倍设置,宽度取550mm。抗规减震系数法采用大震时程分析的方式验算支座最大位移,其中时程分析采用7组地震波(2组人工波+5组天然波)的平均最大变形为428mm,如图7所示。而整体分析法则采用复振型分解反应谱法进行验算,罕遇地震CCQC位移最大值为433mm,与时程结果吻合较好。
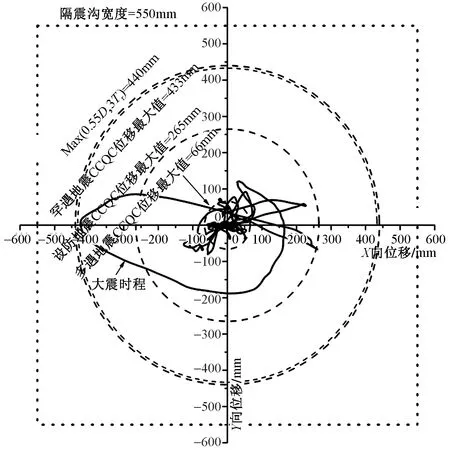
图7 支座位移示意图
(5)使用相同布置的结构模型,进行不同方法设计时,结构的经济性差异主要由各种设计方法导致的内力变化和设计标准引起。采用抗规的减震系数法和整体分析法均按小震弹性设计,而采用隔标进行设计时,构件分为关键构件和普通构件,并分别采用中震弹性和中震不屈服的性能目标进行设计(表7)。本工程关键构件为隔震层托墙转换梁,普通构件为框架梁、柱和剪力墙。
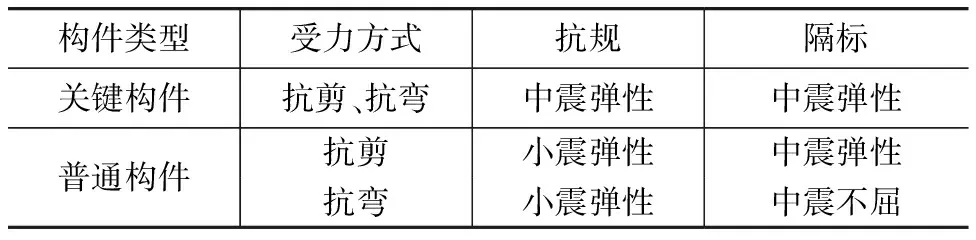
表7 不同设计方法的性能目标
按照不同设计方法,考虑各种不利荷载组合进行配筋设计,得到各类构件配筋面积对比情况,提取转换梁最大下铁配筋、框架柱最大单侧配筋、框架梁最大上铁配筋、剪力墙最大单侧水平筋,见图8。由图8可知,以用钢量从高到低排序:隔标>抗规减震系数法>抗规整体分析法;相比抗规,按照隔标设计时,关键构件的配筋增量较大,普通构件的配筋增量较小;按照抗规设计时,采用整体分析法比减震系数法用钢量略低;相比抗规,普通构件按照隔标设计时,底层用钢量增量较大,顶层用钢量与抗规持平或略低。与楼层地震剪力的衰减规律一致。
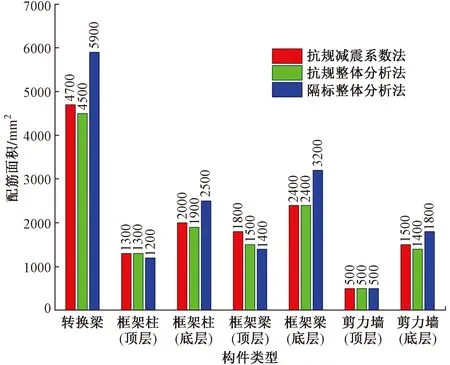
图8 各类构件配筋面积对比
综合考虑三种计算方法下各种构件的配筋总量,并假定三种计算方法的板配筋量相同,以抗规减震系数法的用钢量为基准,抗规整体分析法用钢量约降低3%,隔标整体分析法用钢量约增加8%。
2 设计要点
2.1 楼、电梯穿隔震层构造
本工程地上结构为框架-剪力墙体系,利用楼梯间、电梯间设置围合的混凝土筒体满足结构刚度要求。但也对楼梯、电梯穿越隔震层造成了不便。对于单独设置的楼梯或电梯,采取转换梁的方式处理,在隔震层顶板设置转换梁承托地上剪力墙,地下部分单独设置框架楼梯间或框架电梯间,如图9所示。
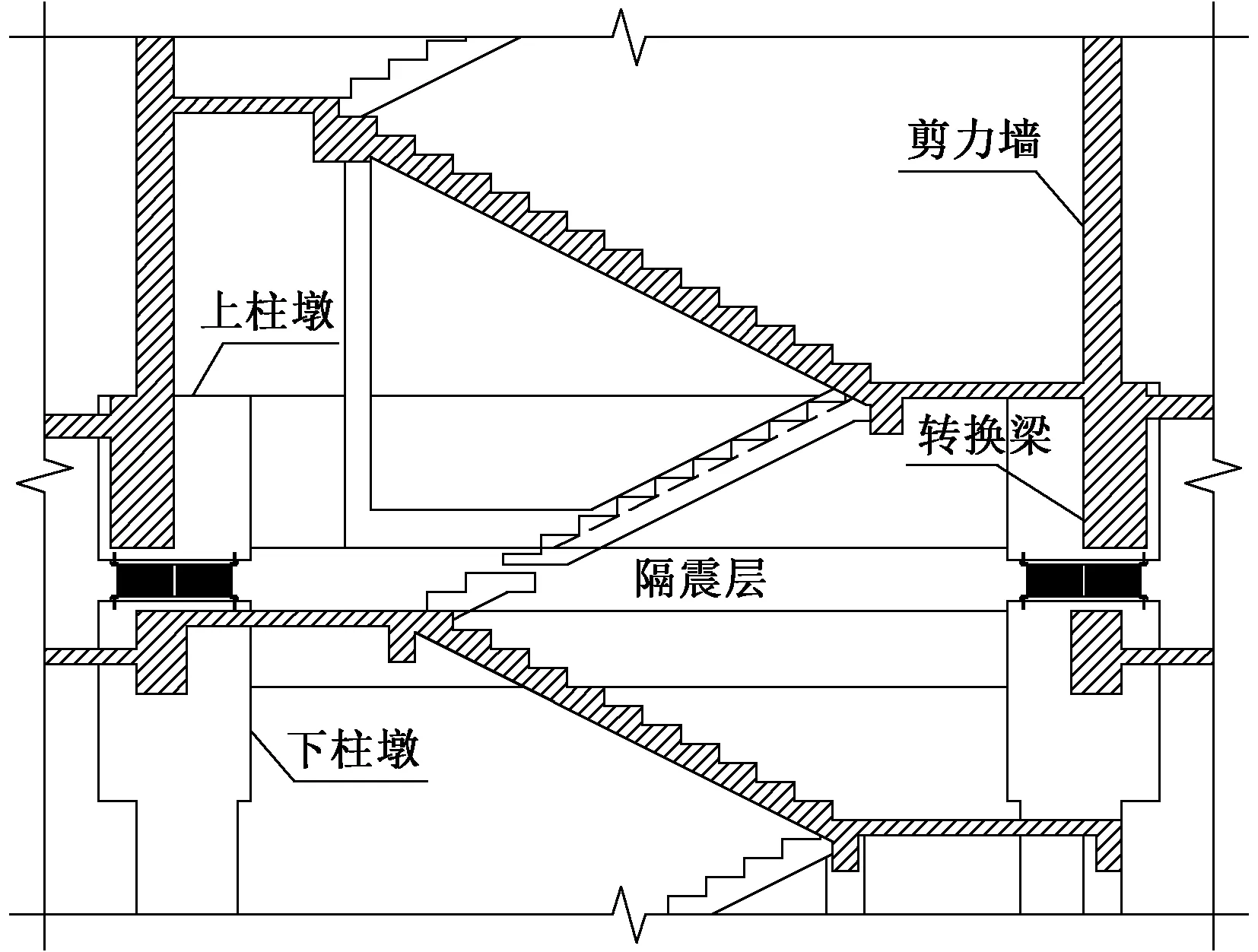
图9 单独楼梯穿隔震层
对于楼梯和电梯相邻设置时,若采用隔震层顶转换的方式,转换梁宽度会影响楼梯净宽或电梯间的位置。本工程采用托挂结合的方式进行处理,楼梯间剪力墙下沉至地下室,由基础底板的隔震支座承托,电梯筒重量较轻,采用钢结构悬挂处理,电梯筒框架依附于楼梯剪力墙侧,与地上隔震结构连为一体,并通过隔震沟与地下非隔震结构脱离,如图10所示。此构造使隔震层出现错层,需控制错层位置在罕遇地震作用下,层间位移角不大于1/1 000,保证隔震装置共同工作。此类错层隔震构造目前在PKPM或YJK中模拟困难,一般采用简化的非错层模型模拟,并在ETABS中进行校核验算。
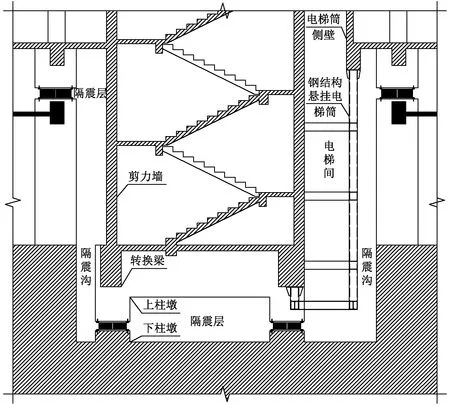
图10 楼梯与电梯托挂结合穿隔震层
2.2 大跨度隔震层
采用抗规减震系数法设计时,由于隔震支座刚度相对于混凝土柱小的多,为了使模型受力状态更接近实际,将隔震上支墩下端简化为铰接约束。但是,由于隔震上支墩一般截面尺寸较大,长度较短,导致其线刚度较大,采用柱底铰接模型计算时,重力荷载在梁端产生的负弯矩,大部分被上支墩按刚度分配了,而其他相连的梁、柱分配的弯矩较小。采用整体计算模型分析时,上支墩刚度与隔震支座刚度串联,形成一个较小的水平刚度,重力荷载作用下,与支墩相连的梁、柱将分配到更大的弯矩。因此采用柱底铰接模型会低估重力荷载作用下,与隔震上支墩相连梁、柱的弯矩。
对于隔震层常规跨度(8m左右)的框架,主要由地震作用控制内力,以上问题并不突出,计算显示对梁下铁配筋并无显著影响。然而,对于隔震层存在的大跨度(18m左右)结构,重力荷载的效应影响显著。图11为本工程隔震层局部大跨度框架在重力荷载作用下分别按柱底铰接模型和考虑支座真实刚度的整体计算模型计算的弯矩分布图,可以看出,相比反映真实刚度的整体模型,柱底铰接模型中大跨梁跨中正弯矩被低估了约1.36倍,隔震层以上柱底弯矩被低估约1.6倍。
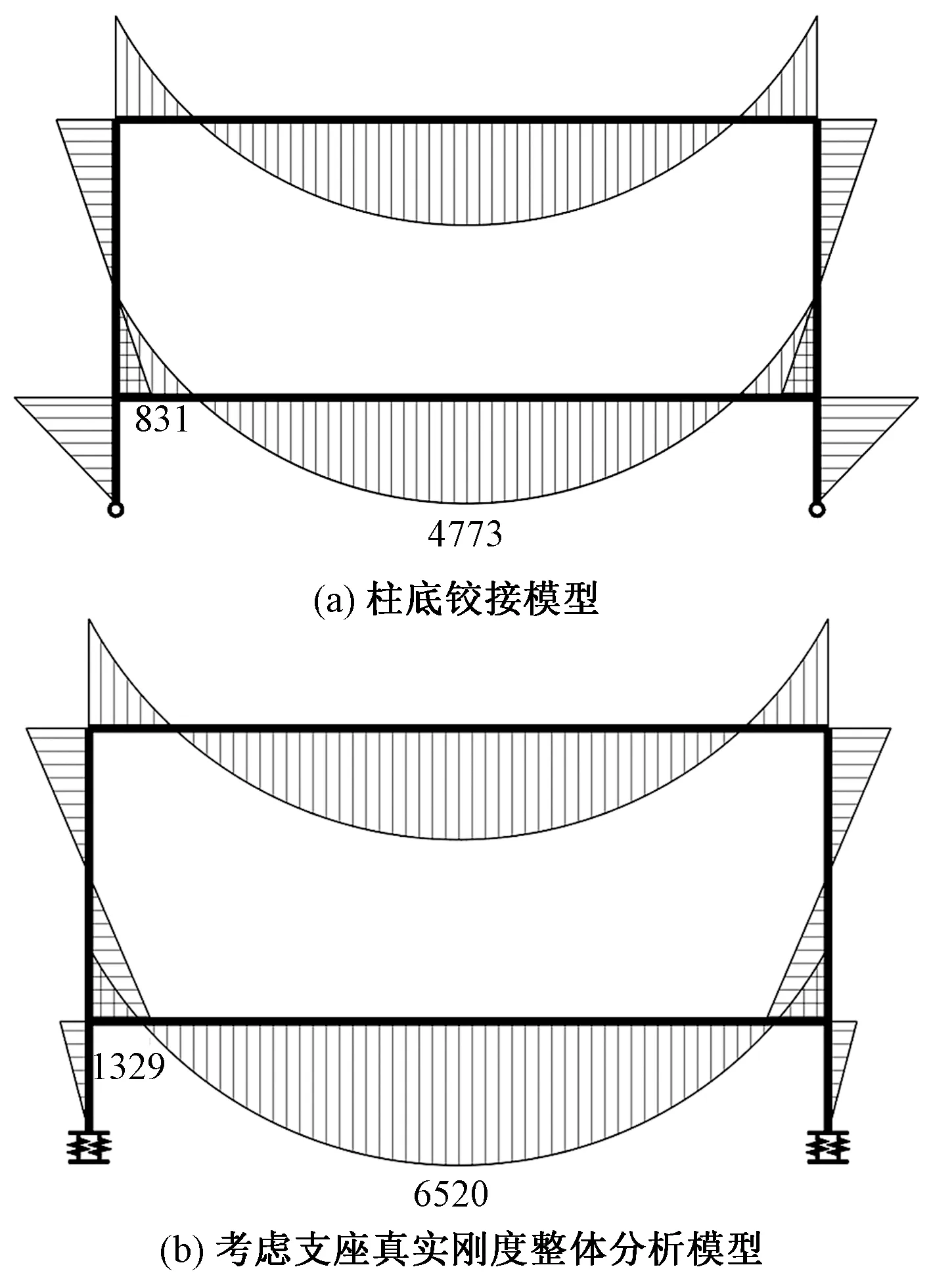
图11 重力荷载作用下弯矩分布图/(kN·m)
因此,与隔震支墩直接相连的大跨度结构,应采用考虑支座真实刚度的整体计算模型进行校核计算。
3 结论
本文通过对比同一工程项目采用不同隔震设计方法产生的指标差异,梳理了三种设计方法的特点及经济性情况,同时,针对楼电梯穿隔震层、大跨度隔震层设计的关键问题进行了论述,形成以下结论:
(1)与抗规减震系数法中直接指定隔震支座刚度,并通过剪切性能偏差调整系数来兼容一定的误差不同,采用隔标整体分析法或抗规整体分析法时,需按实际情况输入支座的参数信息,并通过等效线性化迭代,得到结构在不同地震作用下的动力特性。
(2)与抗规减震系数法相比,隔标整体分析法用钢量略有提升,主要体现在底层构件和关键构件上。抗规整体分析法用钢量最低,隔震效果达到约1度半,可能存在高估隔震效果的可能,需结合工程实际情况谨慎论证后采用。
(3)采用柱底铰接模型会严重低估隔震层大跨度框架梁的跨中弯矩,采用抗规减震系数法设计时应单独复核大跨梁下铁配筋。建议抗规减震系数法应用于常规跨度隔震结构,大跨度隔震结构应采用整体分析法。

