精心预设 关注生成——谈一堂数学好课的建构

⦿ 山东省聊城第一中学 王建明

时间紧、任务重是高中数学教学的重要特征.为了抢时间、赶进度,一线教师课前都会精心筹备,力争应用好宝贵的课堂时间,上好每节课.那么,什么样的课才是好课呢?是讲更多的知识、做更多的题吗?答案自然是否定的,单一的知识讲授已不适合现代教学.当今社会需要具有自主学习能力和独创精神的新型人才,为此教师在教学中需要改变传统的“以师为主”的教学模式,注重学生独立思考和自主学习能力的发展.总之,在教学中应凸显学生的主体地位,切勿为了求急、求快而“越俎代庖”.

在教学中,教师要为“好课”做一个合理的定位,这样才能朝着这一目标开展教学活动,进而形成一个更为科学、高效的教学体系,促进学生全面发展.笔者以“基本不等式及其证明”为例,谈谈自己对“好课”的认识,供借鉴.

1 结合学生认知,设计教学预设

众所周知,课堂的主角是学生,在教学中只有充分调动学生的积极性才能使课堂呈现勃勃生机,为此教师在组织教学活动时应“以生为主”.为调动学生参与的积极性,教师就要去了解学生、研究学生、理解学生,这也是开展“以生为主”教学活动的前提和保障.只有认真地了解学生,才能设计出符合学生认知、适合学生发展的分层的、合理的教学目标,进而让每个学生都能够有所提升;只有研究学生,才能发现学生的闪光点,进而通过合理放大让学生收获学习信心,培养学生健康心理;只有真正理解学生,才能尊重学生,进而深入到学生中去建立一个平等、和谐的课堂环境.

以“基本不等式”为例,在本节课教学前,笔者通过深入钻研教材、了解学生,发现若想学好本节内容,需要学生具备一定的猜想能力和总结归纳能力.虽然学生这方面的能力较为薄弱,但本节内容较为简单,若教师能够正确引导,完成本节内容的探究应该毫不费力.同时,学生之前已经较好地完成了不等式性质的探究,为本节课的学习打下了坚实的基础,加之大多学生对数学学习有着一定的兴趣,这也为学生更好地参与课堂奠定了基础.基于此,在本课教学中,笔者放手让学生探究,进而培养学生独立思考的好习惯.当然,本节课的内容较为抽象,证明时也会遇到一些障碍.例如,基本不等式的猜想及其证明;基本不等式的应用条件;如何应用基本不等式来证明与之相关的不等式;如何建立基本不等式模型;等等.面对可能出现的问题,提前做好预设,进而通过恰当的引导帮助学生疏通障碍,厘清问题的来龙去脉,让学生可以灵活应用基本不等式等相关知识解决更多的实际问题.

针对上面可能出现的障碍,笔者在课前精心预设问题,旨在帮助学生突破困难,收获信心.

设计意图:通过开放性问题的创设为学生提供更广阔的思维空间,引导学生经历猜想、证明、归纳等过程,便于学生对不等式证明形成一个更为系统和全面的认识.

问题2阅读课本,谈谈你对基本不等式不同证明方法的认识.

设计意图:引导学生关注基本不等式不同证明方法间的区别和联系,便于学生在日后证明中可以结合题目特征选择最优的解决方案.同时,在此过程中着重引导学生学会阅读、观察、分析和总结,进而提升学生自主学习能力.

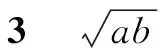
设计意图:引导学生结合图形来理解基本不等式的几何意义,找到另外一种证明方法,进而强化学生的数形结合意识.

问题4下列的不等关系是否正确?

设计意图:借助练习检验学生对基本不等式应用的掌握情况.

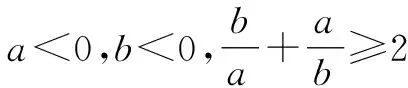
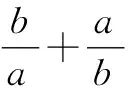
设计意图:借助变式引导学生关注基本不等式的适用条件,避免因忽视条件而产生滥用公式的情况.

这样,结合学生特点,从教学重难点出发,精心预设问题,以期在问题的引导下学生能够通过阅读、探究、交流等活动来突破重难点,顺利完成学习目标.

2 根据课堂生成,调整教学预设

课堂是动态生成的,无论教师如何精心筹备,在教学中都有可能发生“意外”,看一节课是否称得上“好课”就要看教师如何处理这些“意外”.教师理解学生,尊重学生,为学生创设宽松的学习环境,其目的就是让学生全身心地参与到教学活动中来,积极思考,自由表达,进而使知识、能力、情感得到全面发展;然若在教学中忽视这些“意外”,那么势必会影响学生参与的积极性,限制学生思维的发展,不利于学生学习能力的提升.为此,在教学中教师应根据“意外”及时调整教学预设.教师要合理开发和利用“意外”,使之转化为激发学生思考、实践的动力源,让学生的学习更主动、更积极,课堂更高效.

问题6如图1,以长为a+b的线段为直径画半圆,在直径AB上取点C,使得AC=a,BC=b,过点C作垂直于直径AB的半弦CD.看看你有什么发现?

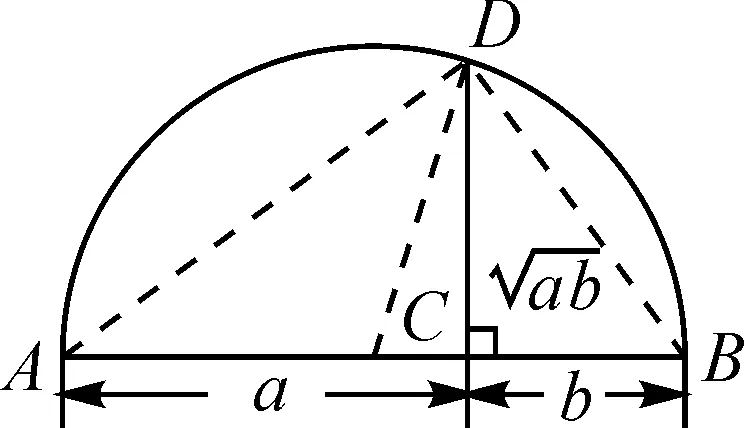
图1

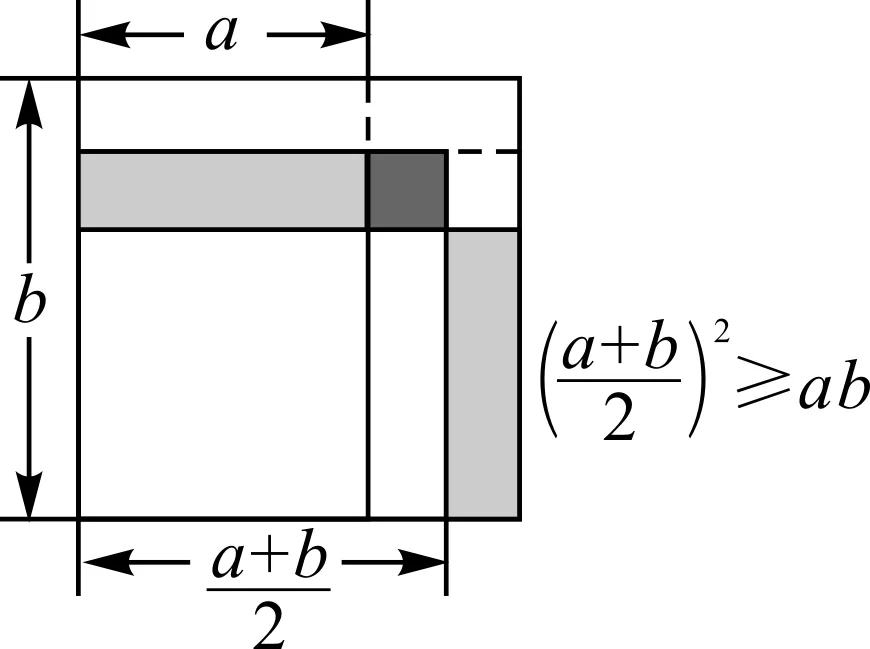
图2

3 注重学习方法,关注合作学习

“教”与“学”是协调发展、和谐统一、相互促进的,其本质是一种互动合作.在教学中应多开展合作学习,通过学生互动交流,彼此启发、互补,进而丰富知识、提升技能,促进学习能力提升.在本节课教学活动中,合作学习主要体现在以下几个方面:

首先,引导学生进行自主学习.师生合作利用比较法证明基本不等式后,引导学生通过自主学习的方式探究利用综合法和比较法证明基本不等式.为了提升自主学习效果,使学习更具目的性,笔者提出如下两个问题:(1)对比两种证明方法,谈谈它们有哪些特点,有哪些区别与联系?(2)你更喜欢用哪种方法来证明呢?这样通过问题诱发学生关注不同证明方法的本质区别,有利于后期的合理应用及自主学习能力的提升.

其次,培养学生问题意识.问题是合作的基石,有问题才能更好地沟通,在教学中应鼓励学生提出问题.例如,在本节教学活动中,通过变式问题,引导学生关注a,b的正负,进而揭示不等式成立的条件.

最后,关注合作学习.在学习过程中出现思维障碍是在所难免的,如何突破障碍就成了课堂教学的焦点.不同的学生其思维方式不同,遇到的困难也会有所不同.对于一些困难不大的问题,可以放手让学生进行合作探究,集思广益,在交流与合作中互相促进,共同成长.例如,在探究基本不等式几何意义的过程中,当学生构造图形出现障碍时,笔者及时进行了引导,待思路打开后学生又进行了不同的尝试.给予学生足够的时间和空间进行建构,不仅凸显了学生的主体地位,而且激发了学生的探究热情,取得了较好的效果.

总之,评价一节“好课”不能简单地看学生学会了多少知识,教师讲了多少道题,也不能简单地看课堂氛围是否活跃,而是要从学习态度、学习习惯、创新能力、合作意识等多方面进行综合考量,重视学生综合能力的提升.教学中要打破“唯分论”的束缚,关注学生数学学习兴趣的培养和自主学习能力的提升,继而培养学生的终身学习意识.