极化恒等式妙解向量数量积最值问题

⦿ 哈尔滨师范大学 李思琦

1 极化恒等式

1.1 代数形式

极化恒等式的代数形式为

推导过程:

(a+b)2=a2+2a·b+b2,

①

(a-b)2=a2-2a·b+b2,

②

①-②,得(a+b)2-(a-b)2=4a·b.

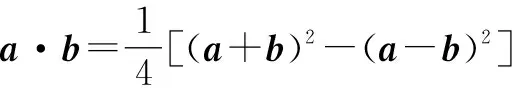
1.2 几何意义

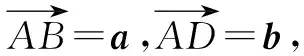
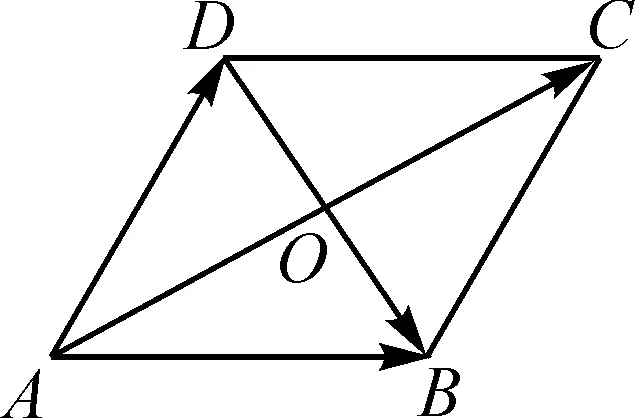
图1

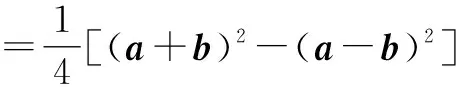
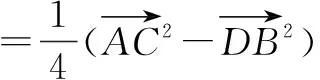
=AO2-OB2.

这样,我们就可以把一组不共线的向量数量积问题转化为以这两个向量为邻边的平行四边形两条对角线平方差的四分之一;在三角形中,可以将其转化为三角形中线长与底边长一半的平方差.

2 极化恒等式的应用

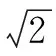
解法一:坐标法.

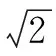
故选:B.

解法二:极化恒等式法.

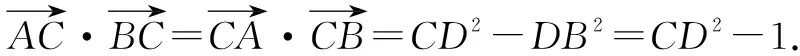
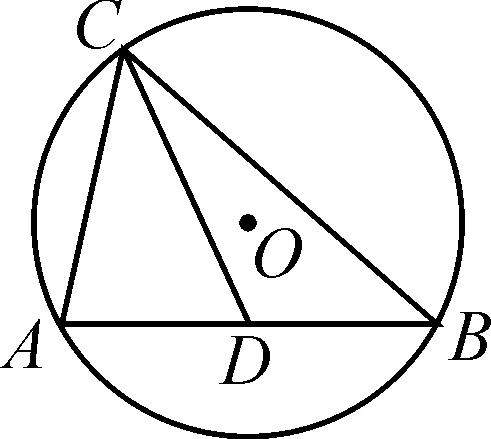
图2

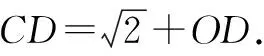
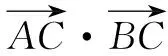
评析:根据向量的坐标运算将向量数量积的最值问题转化为三角函数的最值问题,运算量较大.本题可先将问题转化为同起点两向量的数量积求最值,化动为定,落点于初中几何问题,大大减少运算量.

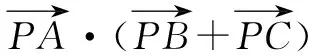
解法一:坐标法.

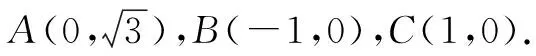
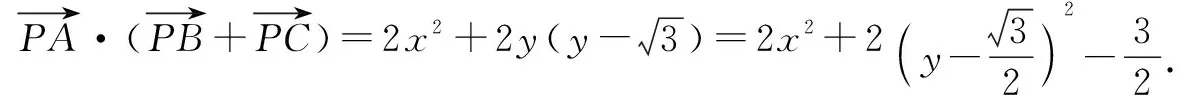
解法二:极化恒等式法.

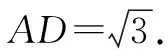
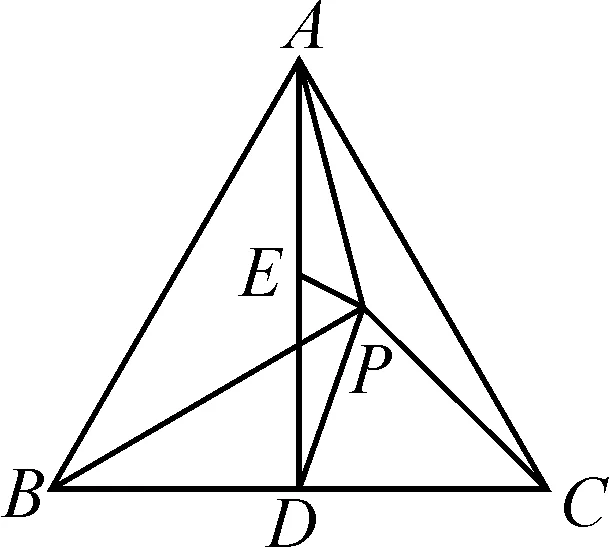
图3

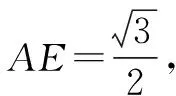
评析:三角形与向量的综合题属于高考经典题,解决此类问题的通法是坐标法,直接、易想,但有时计算量较大.本题用坐标法实现向量与代数的转化,最终将问题转化为求二元二次函数的最值问题.而利用极化恒等式可以完美地把它转化为简单的几何问题.

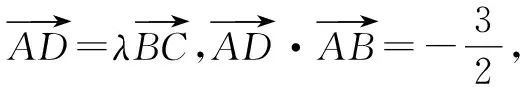
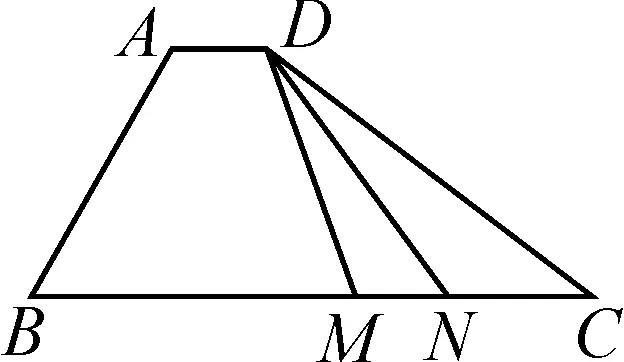
图4

解法一:基底法.

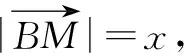
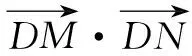
解法二:极化恒等式法.

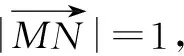
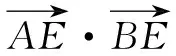
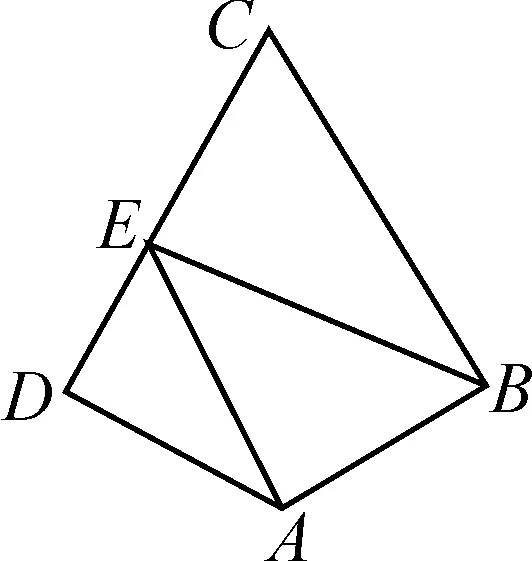
图5

解法一:基底法.

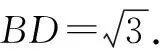
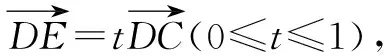
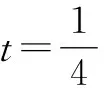
解法二:极化恒等式法.

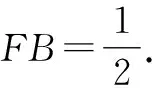
因为F为定点,E为边CD上的动点,所以EF的最小值为过点F作CD的垂线段FG的长.

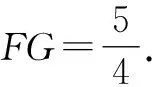
评析:例3和例4分别为高考试卷中填空题和选择题的压轴题,难度较大.对于数量积的最值问题,多数人在解题时会选择利用坐标法或者基底法分解向量,二者本质上都是将问题转化成函数求最值,过程繁冗且计算量较大,容易出错.

例3、例4的解法对比,充分体现了极化恒等式在解决平面向量数量积最值问题的精妙之处,在一些题目复杂难解、计算量大的情况下,有化繁为简、出奇制胜的作用.

坐标法和基底法作为解决向量数量积最值问题的常规方法虽然易想,但有时过于循规蹈矩导致运算复杂,解题效率不高.而极化恒等式是解决同起点向量数量积问题的强有力手段,完美展现向量与几何之间的转换,快速简化问题.这充分体现了小题小做、小题巧做的思想,为读者提供一种新的解题思路.

解题之道,贵在审时度势,因题择宜.在实际求解向量数量积最值问题时,要根据题目条件和问题表征,从数与形两个角度分析问题,选择行之有效的解题方法和策略.