创新设计,巧妙破解,探究拓展——2021年高考数学上海卷第11题的探究

⦿ 江苏省宿迁中学 徐士权

直线与抛物线的位置关系问题,一直是高考数学试卷中的一类常见考点,设置巧妙,形式各样,变化多端.2021年高考数学上海卷第11题就是以抛物线为问题背景,通过直线与抛物线的位置关系所产生的具体三角形的三边长,创新设置问题,新颖别致,是一道令人眼前一亮的创新题,值得好好研究、挖掘.

1 真题呈现

高考真题(2021年高考数学上海卷第11题)已知抛物线C:y2=2px(p>0),若第一象限内的点A,B在抛物线C上,焦点为F,且|AF|=2,|BF|=4,|AB|=3,则直线AB的斜率为______.

2 真题剖析

该题以抛物线为问题背景,结合抛物线的焦点,以及抛物线上的两点所构造的边长确定的三角形为载体,进而确定抛物线上的两点所对应的直线的斜率.

具体破解时,可以通过直线的斜率公式,结合点差法的应用来处理;也可以通过解析几何的平面几何化,利用斜率的定义,数形结合来直观处理;还可以利用题目中已知的弦长,结合弦长公式代入来求解.无论采用何种方法破解,都离不开抛物线的定义及其应用,借助抛物线定义的转化,或代数运算,或数形结合,或公式应用等,都可以很好地达到目的.

3 真题破解

方法1:点差法.

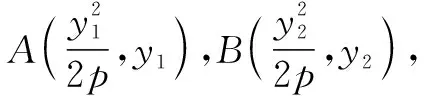
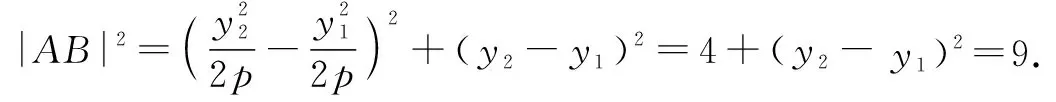
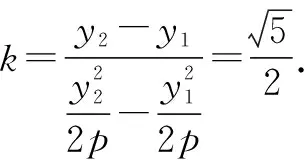
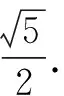
点评:设出两点的坐标,结合抛物线的定义与两点间的距离公式确定参数之间的关系,利用点差法及直线的斜率公式即可求解.利用抛物线定义可以有效转化焦半径问题,实现焦半径与相应点的坐标之间的联系,在处理一些长度问题中经常用到.点差法是处理直线斜率问题比较常用的方法.

方法2:平面几何法.

解析:如图1所示,过点A,B分别作抛物线C的准线的垂线,垂足分别为P,Q,作AM⊥BQ,垂足为M.

图1

根据抛物线的定义,可知|AP|=|MQ|=|AF|=2,|BQ|=|BF|=4,则|BM|=2.

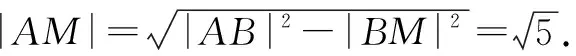
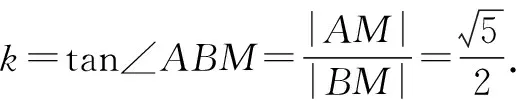
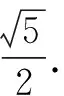
点评:结合抛物线的定义,建立对应的平面几何图形,在直角三角形中,利用勾股定理,以及三角函数来求解对应直线的斜率.利用平面几何法处理解析几何问题,更加直观形象,关键是建立平面几何中点、线、角与对应解析几何中元素的关系,合理应用,巧妙转化.

方法3:弦长公式法1.

解析:设A(x1,y1),B(x2,y2),其中x2>x1>0.

设直线AB的斜率为k,且k>0.

点评:利用弦长公式法求解,简单快捷.借助弦长公式的应用建立相应的关系式,代入相关的数值即可巧妙求解.

方法4:弦长公式法2.

设直线AB的斜率为k,且k>0.

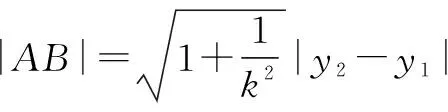
4 变式拓展

探究1:保留题目背景,交换题目部分条件与结论之间的位置——已知抛物线上两点所对应直线的斜率,进而确定这两点间的距离问题.这样变式处理,考查的知识点基本不变,难度比原问题有所下降.

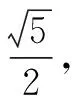
解析:设A(x1,y1),B(x2,y2),其中x2>x1>0.

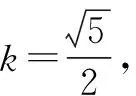
点评:直接根据题目条件,在利用抛物线定义进行转化的基础上,确定两点对应横坐标的差值,再直接利用弦长公式求解对应的弦长即可达到目的.设置更加直接,处理起来更加方便快捷.

探究2:保留题目背景与部分条件,改变原来两点均在第一象限的位置关系,转化为其中一点在第一象限,另一点在第四象限,同时改变这两点间的距离,得到变式2,考点一致,难度相当.

变式2已知抛物线C:y2=2px(p>0),焦点为F,若第一象限内的点A与第四象限内的点B均在抛物线C上,且|AF|=2,|BF|=4,|AB|=5,则直线AB的斜率为______.

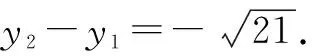
点评:同样,除了利用抛物线的定义进行转化,借助平面几何知识来处理,也可以利用弦长公式求解.具体解答过程可以参照真题的破解方法,这里不多加叙述.当然,改变两点在不同象限内的情况,还可以得到相应的变式问题.

5 教学启示

(1)回归抛物线的本质,抛物线的定义先行

抛物线的定义反映了抛物线自身的本质特征,揭示了相关曲线存在的几何性质与特征规律.在实际破解相关问题中,合理回归、巧妙应用抛物线定义,实现“抛物线上的点到焦点的距离”与“该点到准线的距离”二者之间的合理变形与转化,实现“两点距离”或“点线距离”之间的合理过渡、变形、转化,是破解抛物线问题最常用的一个基本技巧方法.

(2)抓住平面几何特征,破解解析几何问题

解析几何问题本质上离不开平面几何的图形特征,具有平面几何的本质特征.在具体破解问题时,合理引导学生通过数形结合对图形特征、线段数量关系、边角位置关系等加以直观认识,从而转化为相应的问题(三角函数、解三角形、平面向量或平面几何等)进行处理.在解题教学中要有意识地引导和培养学生,利用独特的思维去探索数学,欣赏数学的美.

在实际数学解题教学过程中,不能只停留在解题的表面上,应适当强化解题研究,挖掘问题本质,摒弃题海战术,讲究教学艺术,这样才能真正全面提升学生的解题能力、综合能力、创新能力与应用能力等.