“数”与“形”巧妙融合,“动”与“静”综合应用——一道立体几何题的探究

⦿ 苏州市第三中学校 张 瑜

向量是衔接代数属性与几何图形的一个重要纽带,合理沟通“数”(代数)与“形”(几何)之间的联系,是数形结合的典范之一.而巧妙将向量知识融入到立体几何中,动静直观,数形结合,是数学知识交汇、数学思维融合、数学能力综合等方面表现突出的一个创新点,倍受命题者青睐.

1 问题呈现

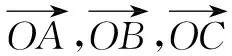
本题以空间向量为问题背景,结合空间向量的长度关系与位置关系,以及数量积的绝对值的不等关系进行创设,有“动”的展示、“静”的确定,动静结合,数形直观,综合考查学生在动态变化情境中的直观想象、空间想象能力等,以及对空间向量投影的理解,进而选择相应的技巧与方法来分析与解决问题.

作为空间向量的综合应用问题,可以从代数运算“数”的视角切入,结合坐标思维来处理;也可以从几何图形“形”的视角切入,结合数量积的几何意义或空间图形的几何特征等来处理.由于视角多变,方法多样,因此在处理过程中需要耐心、细心,以及空间想象能力与数学运算能力的综合显现.

2 问题破解

2.1 思维视角一:代数思维

方法1:坐标+不等式性质法.

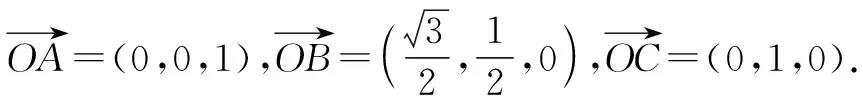
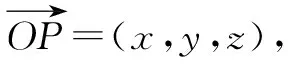
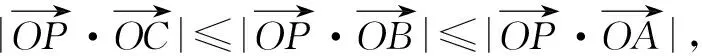
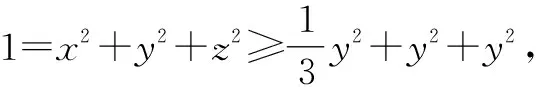
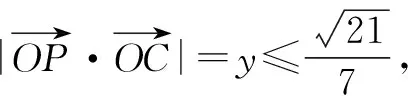
解后反思:根据题设,合理构建空间直角坐标系,确定对应点与向量的坐标,通过向量的数量积公式建立对应的不等式,通过不等式的性质进行消参,进而确定对应的最值.合理构建空间直角坐标系,可以优化数学运算与解题过程,对问题的解决起关键作用.

方法2:坐标+三角换元法.

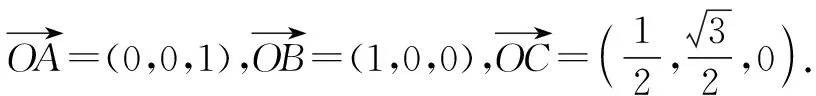
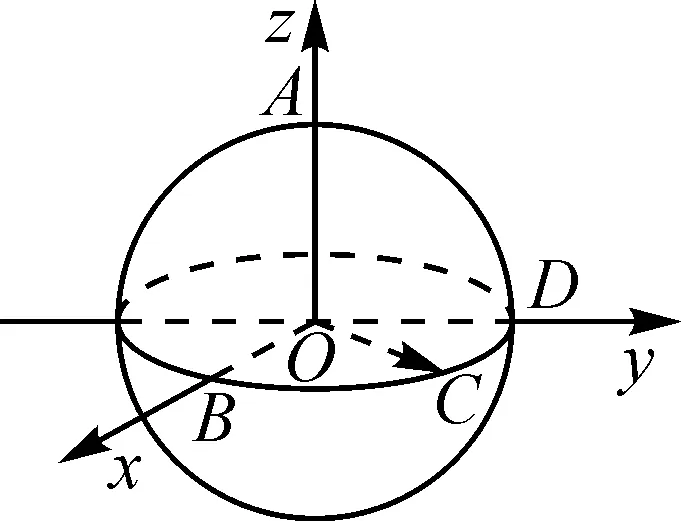
图1

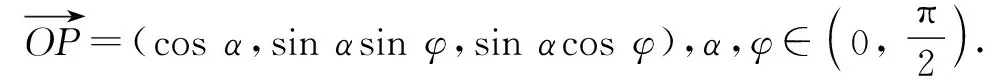
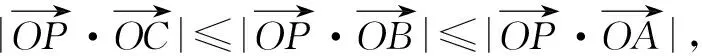
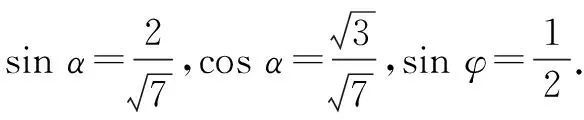
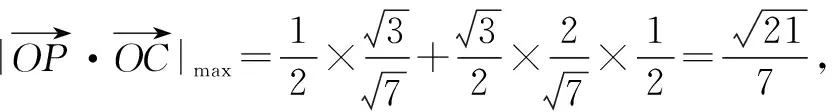
解后反思:三角换元法可以从另一个视角来确定一些相关的最值问题,解决起来更加直接有效.

方法3:空间方程法.

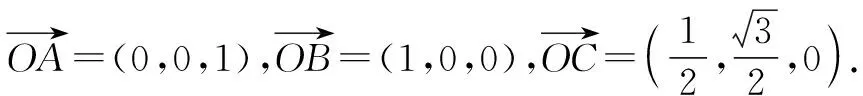
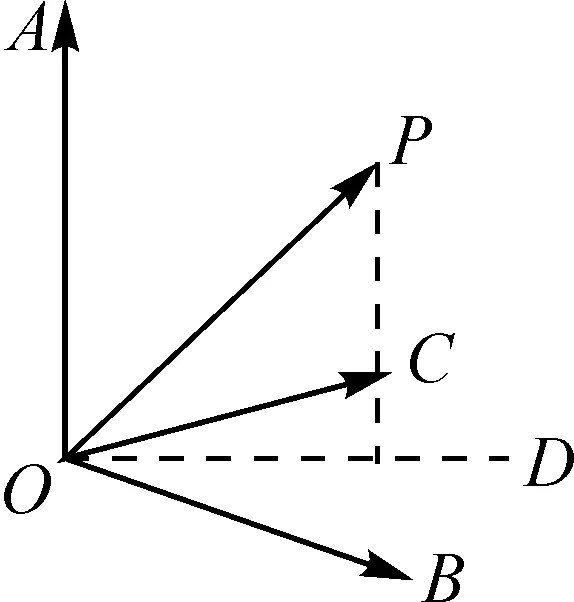
图2

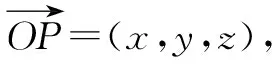
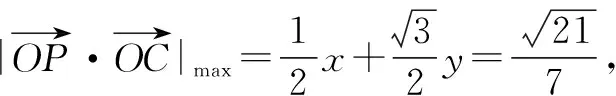
解后反思:利用向量数量积的几何意义确定动点所处的空间中平面位置以及对应的平面方程,结合多条件同时成立来确定对应的参数值,进而得以确定对应的最值.空间中相关平面的确定与方程的构建,是解决问题的一大创新与亮点.

2.2 思维视角二:几何思维

方法4:数量积的几何意义法.

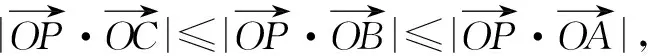
①

由向量数量积的几何意义,可知当且仅当OP⊥平面ABC时,①式等号成立.

不妨设点O到平面ABC的距离为h.

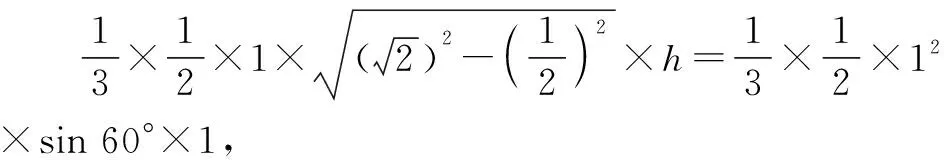
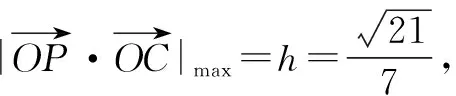
解后反思:利用等体积法,结合三棱锥体积公式的转化,确定等号成立时点O到平面ABC的距离,即可确定对应的最值.抓住最值成立时的条件,逆推思维,有时是解决小题(选择题或填空题)的一种非常有效技巧与方法.

方法5:三余弦定理法.

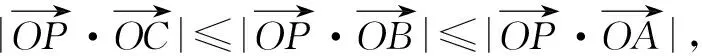
|cos∠POC|≤|cos∠POB|≤|cos∠POA|.

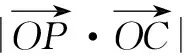
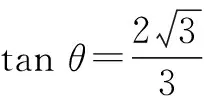
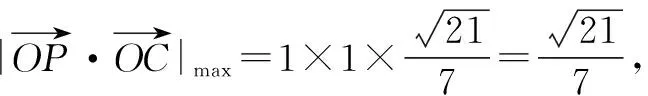
解后反思:回归空间图形的本质,抓住空间的三余弦定理来联系,直观分析,有时也是解决与角有关的问题的一个很好的切入点.

3 变式拓展

探究:保留题目的创新情境与问题背景,合理改变向量的模长以及夹角等相关信息,进行巧妙的改编与应用,得到对应的变式问题.

以上变式问题利用坐标的构建与不等式性质的综合应用来分析与处理,也可以借助其他相关的方法来解决,这里不多加以展开与应用.

4 教学启示

4.1 向量特性,综合应用

《中国高考评价体系说明》要求考查学生灵活运用所学知识分析与解决问题的能力.

向量贯穿高中数学的多个分支,也是衔接不同数学知识模块最便捷有效的桥梁.向量不仅具有代数运算所对应的“数”的本质属性而且具备几何图形所对应的“形”的结构特征,表达方式多样,考查形式多元,思维视角多变,更具灵活性与综合性.

4.2 一题多解,开拓思维

借助一题多解,特别是常规思维与“通性通法”等的应用,可以巧妙开阔思路,发散思维,使得学生学会多层面、多角度分析和解决问题,真正达到对数学原理、基础知识与“通性通法”的认识.同时,数学思维和数学能力等方面都能得到更好的拓宽和加强,达到举一反三、触类旁通的目的.