两道椭圆与圆综合问题的拓展探究

⦿ 甘肃省秦安县第二中学 罗文军

圆和椭圆都是高中数学解析几何部分的重要知识,也是高考考查的重点内容.椭圆与圆综合起来命制的解析几何定值、定点和取值范围问题,可以很好地考查数形结合思想、函数与方程思想和分类讨论思想,以及着力考查数学运算、逻辑推理和直观想象的数学核心素养,因此倍受命题专家的青睐.以下运用类比和特殊到一般的研究方法,对两道椭圆和圆的综合问题进行拓展探究,以期对教师命制模考试题提供参考.

1 试题呈现

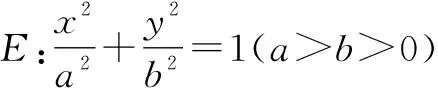
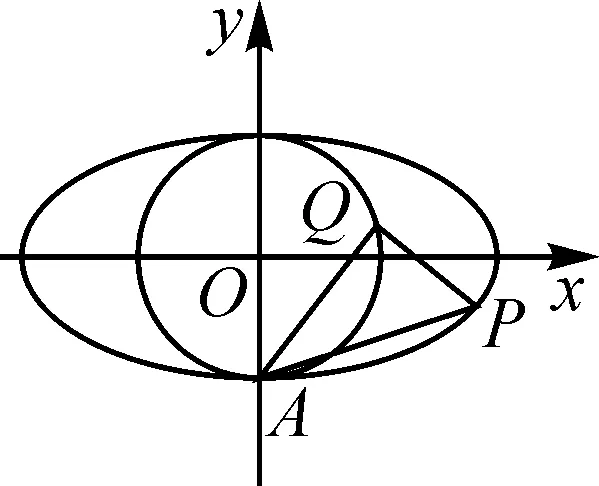
图1

(1)求椭圆E的方程.

(2)A为椭圆E的下顶点,直线AP,AQ的斜率分别记为k1,k2,且k2=4k1,求证:

①△APQ为直角三角形;

②直线PQ过定点,并求出此定点的坐标.

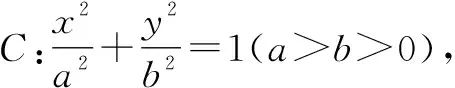
(1)求椭圆C的标准方程;

(2)当点M在圆上运动时,试探究△FPQ周长的取值范围.

2 试题拓展

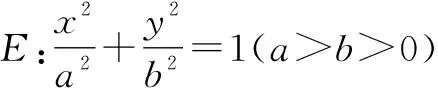
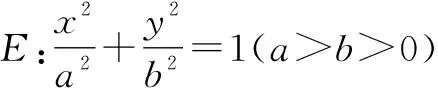
图2

(1)∠AQP=90°;

(2)直线PQ过定点(0,b).

证明:(1)直线AP的方程为y=k1x-b(k1≠0).

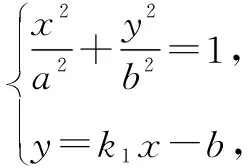
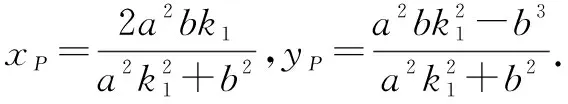
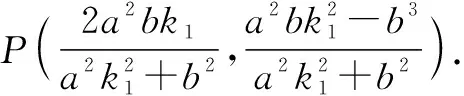
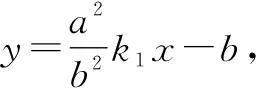
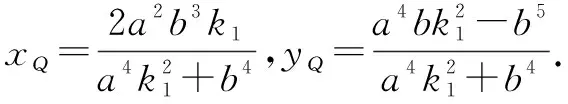
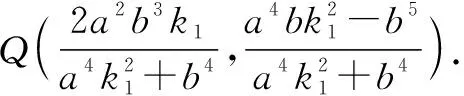
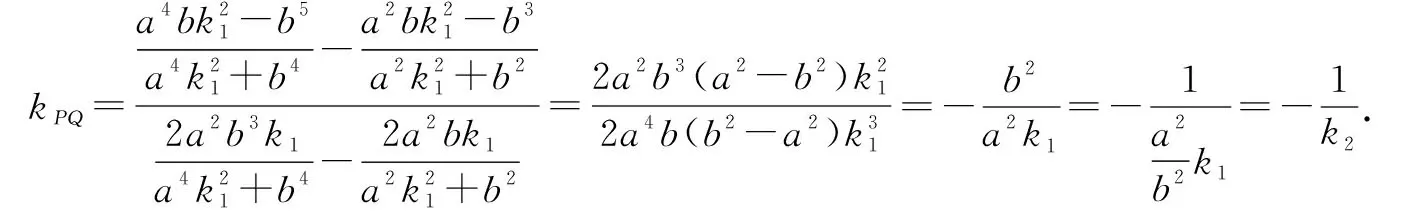
所以kPQ·k2=-1,即PQ⊥AQ.

故∠AQP=90°.

(2)由(1),可得直线PQ的方程为

①

在上述方程①中,令x=0,可得

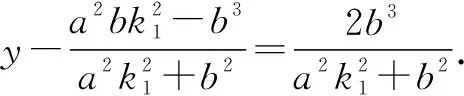
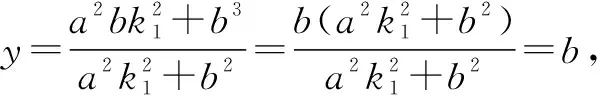
同理可证得下面命题2～4.

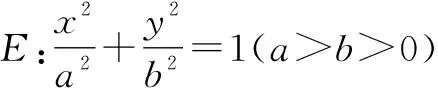
(1)∠AQP=90°;

(2)直线PQ过定点(0,-b).

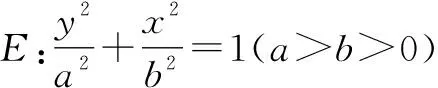
(1)∠APQ=90°;

(2)直线PQ过定点(0,-a).

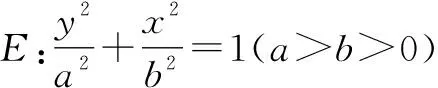
(1)∠APQ=90°;

(2)直线PQ过定点(0,a).

通过对试题2进行拓展探究,可得椭圆及其“姊妹圆”相关性质的命题5.

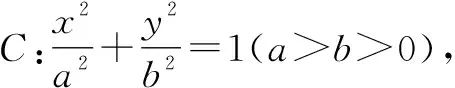
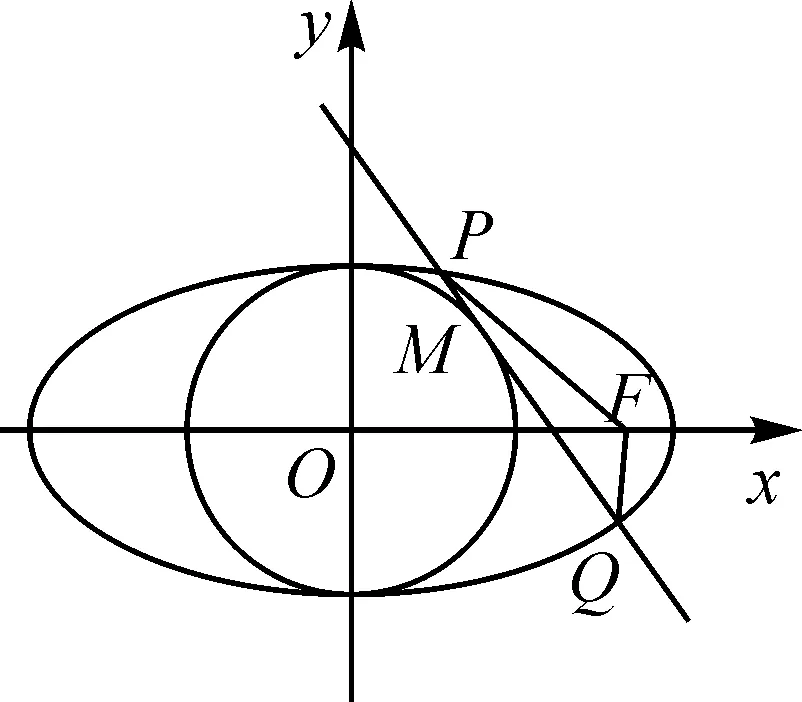
图3

证明略.

3 结束语

著名数学教育家波利亚说过:“发现问题比解决问题更重要.”这句话告诉我们,要学好高中数学,就要认真审视习题,通过对习题的观察,探索习题中蕴含的规律.本文中的解题,没有仅停留在题目的解出上,而是通过观察题设条件中式子的结构特征,运用类比推理和演绎推理的研究方法,顺势对试题进行拓展探究,得到了关于椭圆及其“姊妹圆”性质的五个命题,揭示了这类问题的题根,为高中生数学探究能力的培养提供了素材,为打造高品质高中数学习题课提供了案例.