提升思维能力 优化解题思路

⦿ 江苏省如皋市第一中学 夏 娟

笛卡儿曾说过:“我解决的每一个问题都会成为用以解决其他问题的法则.”下面笔者以一道解析几何题抛砖引玉,说明如何帮助学生强化问题意识,积累解题经验,提升思维能力,优化解题思路,把握数学本质.

1 试题呈现

2 解法研究

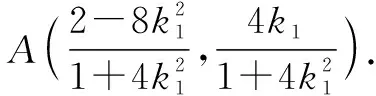
点评:整个过程思路流畅,但运算繁冗复杂,稍有不慎,前功尽弃.学生容易想到思路方法,但不易获得最终结果,往往半途而废者较多.数学运算作为高中数学六大核心素养之一,教师在教学过程中,不能怕浪费时间,而应有意训练培养.

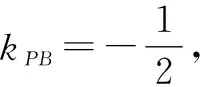
点评:特殊不能代替一般,此类方法在选填题中可作为首选,往往能达到事半功倍之效,但解答题还需结合视角1中获得的A,B两点的坐标来证明一般情况下也成立.

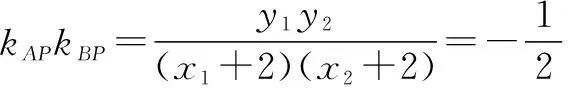
点评:围绕所求目标,选择直线最佳表示形式联立方程组,紧扣题中所给条件,利用韦达定理整体代入,找到参数m与k的关系.

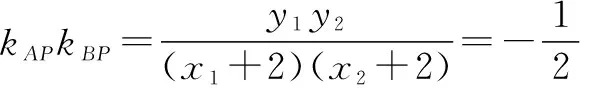
点评:此法有效避开了直线斜率是否存在的讨论,优化了整个计算过程,较之视角3的解法,解题过程更加简洁明了.

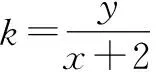
点评:本题的解法灵活多变,从不同视角、不同高度入手均可得到解题的思路.其中,视角1运算繁琐,视角2要证明一般性,视角3要讨论斜率存在与否,视角4不易想到“反”表示直线,视角5斜率形式难配凑.五个视角,五种解法,各有千秋.

在学习中体验数形结合、分类讨论、化归转化(特殊到一般)多种数学思想的交替使用,合理选择直线的表示形式.学生在学习过程中要独立思考、尝试解答,重视思维训练,强化有效运算,通过相互交流、展示解法、提炼总结,认清各种方法的优劣,掌握解决此类问题的通解通法.

3 变式探究

本题若仅限于解法的研究,则有点浅尝辄止.波利亚曾说过:“观察可能导致发现,观察将揭示某种规律、模式、定理.”进一步观察探究例题,可得到一系列变式训练来巩固研究成果.数学学习是理性思维,需要在已知条件和所求目标之间搭建解决问题的桥梁,而数学思想方法提供了解决问题的具体路径.在教学中要鼓励学生从不同的角度进行探索求知,并将所学数学知识和思想方法有效地串联起来,分析和解决问题.

3.1 由一点引直线变为由两点引直线

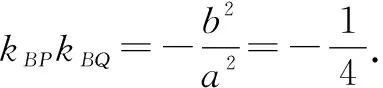
3.2 条件和结论互相置换

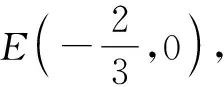
3.3 将由定点引直线改为过椭圆外一动点引直线

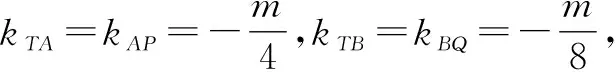
4 教学启示

原试题将直线和椭圆有机结合,题干简洁,构思巧妙,既考查了椭圆方程的基础知识,又考查了区分度极高的定点、定值问题,是解析几何中的常考题型.新课标强调“四基”,即学生通过数学课程的学习,能获得未来发展所需要的基础知识、技能、思想及基本生活经验.这就要求教师在教书育人过程中立足基础.类似第(1)问在训练中要做到又快又准,但同时又要适应高校选拔人才的需求,因而对一些重要题型要深挖其内涵与外延.高考题源于课本但又高于课本,绝大多数题目是由课本中的典型例题或习题演绎而来.解决问题时要求学生能抽丝剥茧,识得庐山真面目.随着“双减”政策的普遍实施,如何在有效的时间内使教学效益最大化,是当下教师应当思考并解决的问题.笔者常年耕耘高中教学一线,发现仍有少数教师热衷于“题海战术”,搞得学生疲乏劳累,苦不堪言.这种“高投入、高污染、低产出”的发展模式,对学生成长产生的破坏性影响往往是不可逆的.我们要着力提倡围绕典型例题进行教学设计和强化训练,总结阐述深刻的数学思想方法,在理解的基础上让学生思维活络起来,培养学生解决数学问题的敏锐直觉,学会分析与解决问题,而不是一味“刷题”.