变换视角,扭转乾坤
——参悟转化与化归思想

2023-10-16 01:13江苏省张家港市沙洲中学刘华珍

中学数学 2023年19期

⦿ 江苏省张家港市沙洲中学刘华珍

“抓基础知识,重化归转化”是学好中学数学的一把“金钥匙”,也是一个基本窍门.事实上,数学学习中的转化与化归思想比比皆是,方方面面,林林总总.在认知层面上有未知向已知的转化,在思维层面上有高维向低维的转化,在空间感观上有空间向平面的转化,等等,其中都有转化与化归思想的“影子”与体现.

1 一般与特殊的相互转化

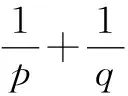
分析:根据题目条件,过焦点F作垂直于y轴的直线交抛物线于P,Q两点,可以快速确定线段PF与FQ的长度.

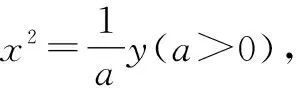
故选择答案:C.

点评:此题若利用直线与抛物线的位置关系来处理,过程比较复杂,运算量也比较大.而利用特殊化处理,简单快捷.特别是涉及此类定值或常值问题,往往可以化一般值为特殊值,从而更加简洁迅速得到所需要的答案.

2 正与反的相互转化

例2若二次函数f(x)=4x2-2(p-2)x-2p2-p+1在区间[-1,1]内至少存在一个值c,使得f(c)>0,则实数p的取值范围为______.

分析:根据题目条件,利用正与反的化归与转化,先求解不等式f(c)≤0恒成立时p的取值范围,再通过取补集来确定所求的实数p的取值范围.

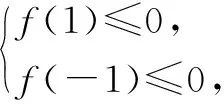
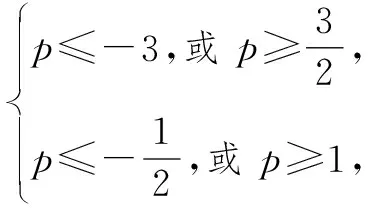
点评:此题的解析过程充分展示了正与反的转化,直接从所求结论入手往往情况较多且复杂,而取其结论的反面,一般所求情况比较单一或直接,这样处理就真正体现了“正难则反”的原则.利用“正难则反”原则处理问题时,经常通过取补集利用间接法,解决一些含有“至多”“至少”及否定性命题情形的相关问题.

3 常量与变量的相互转化

例3(2021年浙江省普通高中学业水平合格性考试数学仿真模拟卷)设函数y=(log2x)2+(t-2)·log2x-t+1,若t∈[-2,2]时,y恒取正值,则x的取值范围是______.

分析:根据题目条件,借助转化与化归思想改变常量与变量的关系,构建一次函数y=f(t)=(log2x-1)t+(log2x)2-2log2x+1,根据变量t∈[-2,2]时,y恒取正值,得到对应的不等式组,通过求解不等式(组)来确定变量x的取值范围.

解析:构建函数y=f(t)=(log2x-1)t+(log2x)2-2log2x+1,则知函数f(t)是关于参数t的一次函数.

当t∈[-2,2]时,由不等式f(t)>0恒成立,知f(-2)>0,且f(2)>0,代入可得

解得log2x<-1,或log2x>3.

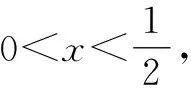
点评:此题若按常规法视x为主元来解,需要分类讨论,这样会很繁琐.而通过常量与变量的转化,将原问题巧妙转化为一次函数的相关问题,即可完美解决.特别是在处理多变元的数学综合问题时,经常借助题设中的常数(或参数)转变视角,合理化归,巧妙减元,实现“主”与“次”的转化.

4 相等与不等的相互转化

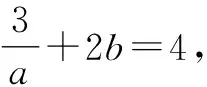
分析:通过双变元方程的消元处理,结合目标构建对应的方程,利用关于参数a的一元二次方程有正数解,通过判别式非负建立不等式,实现相等与不等之间的转化,进而求解对应的参数值的最值问题.

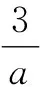
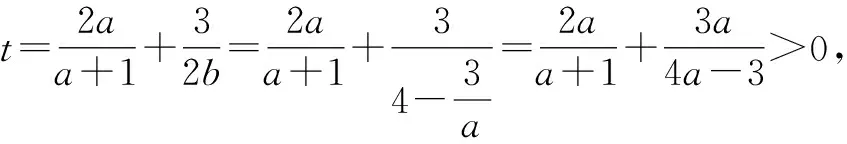
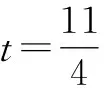
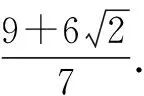
点评:例4结合题目“相等”关系的应用,通过相关数学知识构建“不等”关系,合理转化与化归.特别地,在解决一些函数与方程、基本不等式、导数等问题中,经常用到相等与不等的相互转化思维,巧妙合理建立二者的内在联系与转化纽带.

5 几何体之间的相互转化

例5如图1所示,已知多面体ABCDEFG中,AB,AC,AD两两互相垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,则该多面体的体积为______.

图1

分析:根据题目条件,直接求解该多面体的体积无法下手,而合理借助空间几何体的分割法或补形法,即可实现空间几何体的转化与化归.

解法1:(分割法)过点C作CH⊥DG于点H,连接EH,如图2,将不规律的多面体分割成一个直三棱柱DEH-ABC和一个斜三棱柱BEF-CHG.

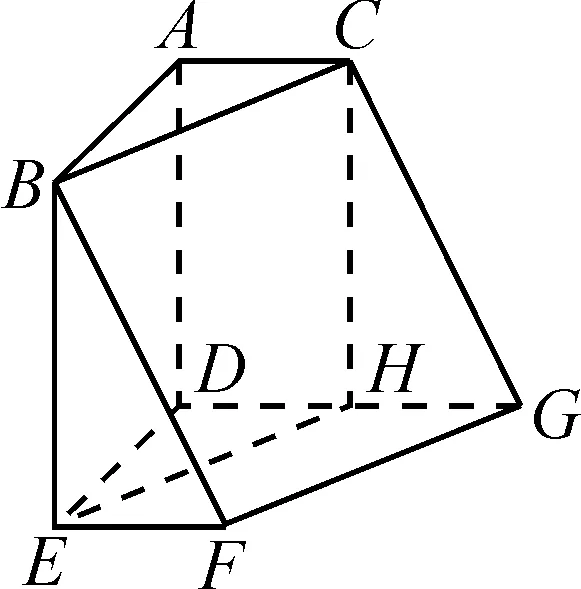
图2

所以V多面体ABCDEFG=2+2=4.

故填答案:4.

解法2:(补形法)如图3,进行补形处理,将原多面体放置于棱长为2的正方体中,结合图形的结构特征,可知所求多面体的体积恰好是该正方体体积的一半.

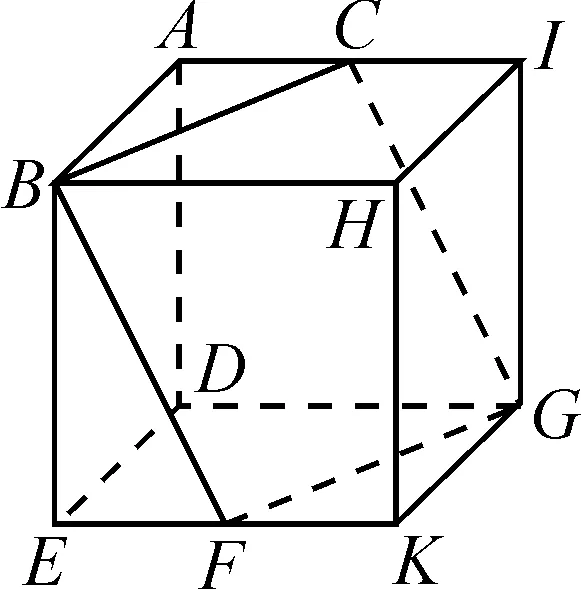
图3