2022年高考立体几何的命题考查与分析
⦿ 江西省赣州市赣县中等专业学校 蔡建华
笔者对2022年全国甲、乙卷,新高考卷以及自主命题的北京卷的立体几何试题进行分析,发现2022年高考中立体几何部分的试题更加关注场景设计与设问技巧,合理倡导回归教材、教学衔接与教学指导,为进一步落实数学核心素养与教学改革指明方向.
1 紧扣教材,引导教学回归
例1(2022年高考数学全国甲卷理科·15)从正方体的8个顶点中任选4个,则这4个点在同一个平面的概率为______.
分析:根据题意,由组合数公式计算“从正方体的8个顶点中任选4个”的取法种数,特别关注其中“4个点在同一个平面”的情况,由古典概型公式计算可得答案.
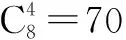
记A=“这4个点在同一个平面”,则A包含底面2种和侧面4种、对角面6种,一共12种情况.

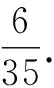
点评:试题以古典概型的求解来创新设置,而实际考查的是正方体的几何性质与图形结构特征,利用正方体中点、线、面等相关元素的位置关系进行直观分析,结合合理的计数问题来解决,实现知识的交汇,强化数学思维的开拓与应用.而问题考查的实质还是正方体、长方体、圆柱、球等这些基本空间几何体的结构特征以及对应的几何性质,要求学生对这些基本图形、基本性质、结构特征等“烂熟于心”,并会加以直观想象与实际应用.
2 依托基本图形,落实“四基”“四能”
例2(2022年高考数学新高考Ⅰ卷·9)(多选题)已知正方体ABCD-A1B1C1D1,则( ).
A.直线BC1与DA1所成的角为90°
B.直线BC1与CA1所成的角为90°
C.直线BC1与平面BB1D1D所成的角为45°
D.直线BC1与平面ABCD所成的角为45°
分析:根据题意,以基本的正方体为图形背景,通过正方体的几何性质,结合线线垂直、线面垂直的性质与判定等判断选项A,B;结合直线与平面所成角的概念与性质来分析并判断选项C,D.
解析:在正方体ABCD-A1B1C1D1中,因为BC1⊥B1C,BC1⊥A1B1,所以BC1⊥平面A1B1CD,于是BC1⊥DA1,BC1⊥CA1,故选项A,B正确.
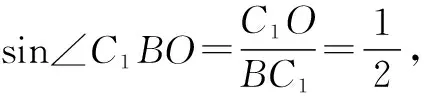
而直线BC1与平面ABCD所成的角为∠C1BC=45°,故选项D正确.
综上分析,故选择答案:ABD.
点评:试题命制意图在于依托正方体这一基本图形,借助异面直线所成的角、直线与平面所成的角等概念与性质的应用,考查基础知识与基本能力.此类依托基本图形的立体几何问题,借助基本概念与基础知识的考查与应用,注重通性通法,淡化特殊解题技巧,全面落实数学的“四基”与“四能”,也为高中数学教学与改革指明方向.
3 注重几何联系,凸显几何直观
例3(2022年高考数学北京卷·9)已知正三棱锥P-ABC的六条棱长均为6,S是△ABC及其内部的点构成的集合.设集合T={Q∈S|PQ≤5},则T表示的区域的面积为( ).
分析:根据题设条件,设点P在底面ABC内的投影为点O,根据正三角形的性质求得OA的长,并结合勾股定理求得OP的长,结合几何直观,进而知动点Q表示的区域是以O为圆心,1为半径的圆及其内部,从而得以分析与求解.
解析:如图1,设点P在底面ABC内的射影为点O.

图1
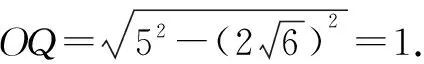
所以动点Q的轨迹是底面ABC内以O为圆心,半径为1的圆及其内部区域,则其对应的面积为πr2=π.
故选择答案:B.
点评:试题命制意图在于从一些基本、熟悉、关联或类比的创新情境中,借助数学的眼光,以数学视角来切入,构建对应的数学模型,寻找相应的研究对象与目标元素,发现数量或图形的性质、数量关系或图形关系等,探索解题的途径与方法.此题结合集合语言考查学生的空间想象能力及转化划归思想,引导教学要从立足学生核心素养出发,从基础“有图用图”上升到“无图想图”,突出立体几何的直观想象能力,以及立体几何中“观察、判断、计算、证明”的基本解题途径与基本步骤.
4 关注素养考查,强调能力立意
例4(2022年高考数学全国乙卷理科·9)已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O的球面上,则当该四棱锥的体积最大时,其高为( ).
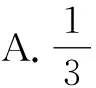
分析:根据题意分析,当四棱锥为正四棱锥时其体积最大.设出四棱锥底面边长,结合勾股定理的应用确定棱锥的高并得出棱锥体积的表达式,利用均值不等式来确定对应的最值,进而求解体积取最值时对应的参数值.
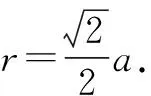
于是,该四棱锥的体积
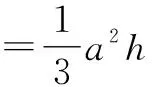
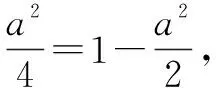
故选择答案:C.
点评:该题为球内四棱锥体积的最大值问题,考查直观想象与逻辑推理等核心素养,要求学生有较强的空间想象能力和分析问题的能力,将问题转化为三次函数的最值问题,可以利用均值不等式来处理,也可以通过函数的构建,利用导数来求解.
总体上来看,通过对全国甲、乙卷,新高考卷以及自主命题的北京卷等相关试卷的命题分析,发现2022年高考立体几何试题的命制继续遵循《中国高考评价体系》,贯彻高考改革与创新,立足“立德树人”,彰显其特殊的育人价值.2022年高考试题中立体几何部分的考查稳中有变,变中有新,更加突出空间想象能力与直观想象素养,同时关注逻辑推理与数学运算,更加关注数学素养与数学品质,以及数学关键能力等各方面的综合与考查.

