让思考成为数学运算的助推器

⦿ 福建省莆田第四中学 林 琴

随着新高考改革步伐的不断迈进,高考更加注重对学生各方面能力的考查与区分,突出核心素养的关键能力.其中,对学生数学运算能力的要求就提到了一个更高的层面,因而提高高中生数学运算能力是一个亟待解决的数学问题.鉴于此,下面结合实例来具体阐述如何处理数学运算问题,让思考成为数学运算的助推器.

1 法则应用的合理性

解决问题中的数学运算过程,就是一个数学法则应用的过程.厘清数学问题的实质与内涵,结合相关问题中所涉及到的概念、定义、公式、定理以及性质等本质,通过数学运算法则的应用,建立联系,直击要害,达到运算法则应用的合理性.

例1(2022年高考数学上海卷·11)若|a|=|b|=|c|=λ,且满足a·b=0,a·c=2,b·c=1,则λ=______.

分析:根据题设条件,确定平面向量的位置关系并构建相应的平面直角坐标系,合理应用平面向量中的相关运算法则,利用平面向量的坐标表示与设置,结合平面向量的模、数量积的坐标公式等构建相应的方程组,即可确定参数的值.

解析:由a·b=0,可得a⊥b.

构建平面直角坐标系,设向量a=(λ,0),b=(0,λ),c=(x,y),x,y∈R,则有x2+y2=λ2,其中λ>0.

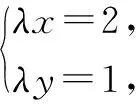
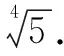
点评:在解决平面向量问题时,经常应用定义法、坐标法与几何法这几种常见的方法来解决.这里,在解决平面向量问题中,借助平面直角坐标系的构建,利用坐标法的代数运算来分析与处理平面向量中的相关问题,是一种更加合理的数学运算法则的应用.借助坐标法,化“形”为“数”,代数运算处理.

2 简便运算的灵活性

结合数学问题中涉及到的基本性质、整体思维、重要结论等,合理构建与问题对应的数学模型或数学关系等,简化运算,全面提升数学运算与数学思维的灵活性,明确运算目标,构建相应的联系,优化解题过程,提升解题效益.

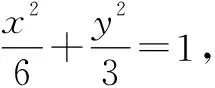
分析:根据题设条件,结合直线与x轴,y轴分别交于两点,利用直线截距式方程的设置,引入对应的参数与方程,结合直线方程的特征,可以快捷简便地确定直线与坐标轴的对应交点问题,方便问题的进一步分析与求解;进而结合椭圆的中点弦性质,为简便运算提供更加灵活与便利的条件.

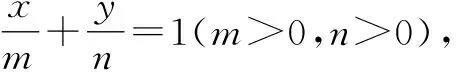
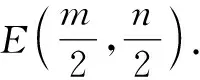
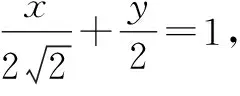
点评:根据题设条件设置合适的直线方程,是简单快捷处理直线与圆锥曲线位置关系问题中的一个重点,也是灵活运算的基础.而熟练掌握圆锥曲线中的一些“二级结论”(本题中用到圆锥曲线的中点弦性质),在破解小题时可以更加灵活便捷,优化数学运算,简化解题过程,提升解题效益,节约宝贵时间.

3 公式选择的有效性

在数学运算前需合理选择公式,同时要根据题目意图进行思考,以目标引领思维,特别涉及到有多种公式可供选择时(主要是三角函数问题、数列问题等),要洞察已知条件与所求结论之间的有效联系,合理数学思维与推理,进行有效性的公式选择,达到“一箭封喉”,真正提升数学运算的准确性.

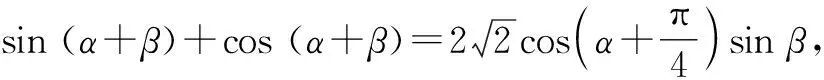
A.tan(α+β)=1 B.tan(α+β)=-1

C.tan(α-β)=1 D.tan(α-β)=-1

分析:根据题设条件,从众多的三角恒等变换公式中进行有效性的公式选择,结合三角函数关系式的结构特征,先利用两角和与差的三角函数公式加以展开,使得复杂角转化为简单角,再综合变形所得的三角函数关系式,“逆向”利用两角和与差的三角函数公式进行转化,最后进行三角函数式的变形与求值.

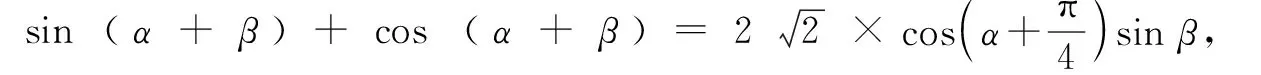
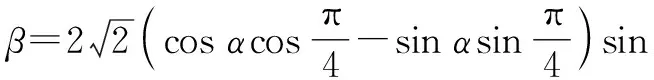
于是sinαcosβ-cosαsinβ=-cosαcosβ-sinαsinβ,即sin (α-β)=-cos (α-β).

所以tan(α-β)=-1.故选择答案:D.

点评:根据题设条件与结论中相应的三角函数关系式等信息,正确利用两角和与差的三角函数公式在复杂角与简单角之间进行“正向”与“逆向”变形处理,有效选取三角函数公式,以最有效、最简便的方式,构建题设条件与结论之间的联系,从而实现问题的分析与解决.

4 路径选取的高效性

数学运算的路径是多样性的,合理的积极思考,可以使得运算路径更加高效、更加直接,进而借助数学运算以及逻辑推理等的综合应用,提高数学运算的效率.

例4(2022年高考数学新高考Ⅱ卷·12)(多选题)对任意x,y,x2+y2-xy=1,则( ).

A.x+y≤1 B.x+y≥-2

C.x2+y2≤2 D.x2+y2≥1

分析:根据题设条件,将条件中的二元方程加以配方处理,转化为两代数式的平方和为1的形式,引入参数进行三角换元,进而选取高效的数学运算路径,结合对应的参数将x+y,x2+y2表示为三角函数关系式,进行恒等变形与处理,利用三角函数的图象与性质来确定对应的取值范围,进而结合选项来分析与判断.

解析:由x2+y2-xy=1,配方可得

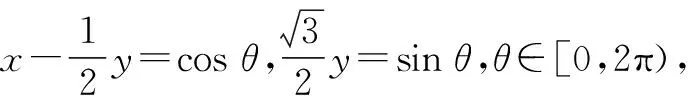
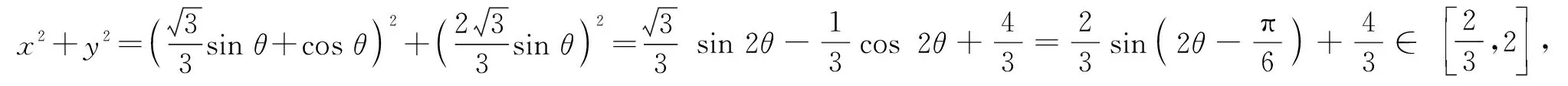
故选择答案:BC.

点评:在破解一些涉及代数式或参数的取值范围或最值,以及不等式成立等相关问题时,经常利用三角换元法,将目标代数式或参数转化为三角函数的形式,借助三角函数的图象与性质来处理,是解决此类问题中比较高效的一种数学运算路径的选取.

在数学教学与学习过程中,完善与提升数学运算能力是一个渐近与螺旋上升的过程.在此过程中,还要不断强化一些其他方面的能力,如敏锐的观察力、整体思维能力、化繁为简的转化能力以及解题全过程的统筹安排能力等,合理调配,不断优化,真正让思考融入到数学运算中去,不断通过思考优化数学运算,通过数学运算促进思考,形成良性循环.让数学运算根植于思考的土壤,借助思考的“翅膀”提升数学运算能力,寻找快乐源泉,让运算过程开出绚丽的思维之花.