发挥作业价值 实现教学相长

⦿ 江苏省通州高级中学 邵春燕

课后作业是教学效果最直接的反馈,是教师了解学生最直接的信息来源,是学生自我检测的重要手段,其在“教”与“学”中的作用是无法被取代的.对于学生,通过做作业可以进一步巩固知识,完成知识的内化,发现学习中存在的漏洞,从而及时进行修补;通过作业拓宽视野,提高分析能力;等等.对于教师,通过作业可以更好地了解学情,及时调整教学进度;通过对作业的分析和整理找到教学中的不足,及时调整教学策略,提高教学质量.然在教学中部分师生只关注作业在巩固知识中的作用,常采用“题海”战术进行强化训练,过多的练习占据了学生反思和总结的时间,这样的课业安排不仅增加了学生的课业负担,而且收益甚微,难以实现“减负增效”的目的.同时,批改作业也会占用教师较多的时间,导致教师不能更好地了解学生,“因材施教”这一教学目标也难以实现,为此,教师在作业的设计上要体现针对性、层次性,充分发挥作业的有效性[1].笔者就如何合理安排来发挥作业的积极作用,谈几点自己的认识,供参考!

1 控制好“度”,把握好“质”

在素质教育的推动下,教师精心设计教学过程,利用分层问题来调动学生参与的积极性,取得了较好的效果.然在课后作业设计上,为了体现“公平”,教师常搞“一刀切”.众所周知,个体差异的存在决定学生的接受能力是参差不齐的,故不同的学生在同样的时间内能完成的作业量也是不同的.因此,若盲目地搞“一刀切”,势必会出现“吃不饱”和“吃不了”的现象,最终使得“吃不饱”的学生难以提升,“吃不了”的学生丧失学习信心,作业的价值难以发挥,为此,教师在作业设计上必须控制好“度”,把握好“质”[2].

(1)“数量”分层

在解同一问题时,学优生的解题效率可能是学困生的几倍,若作业布置的“量”相同,学困生很难顺利完成作业,久而久之,部分学生就会放弃作业,甚至有些学生还会出现抄袭的现象,使课后作业失效.为了改变这一现象,可以让有困难的学生从作业中挑选一些题目认真完成,在“力所能及”的范围内完成作业,以此提升解题信心.当然,这样难免会使一些学生产生惰性心理.为了避免此类现象发生,教师要及时做好激励评价和正向引导,让学生在作业的完成上更加积极和主动,从而在保证质量的基础上实现数量的提升,进而促进解题能力的提升.

(2)“难度”分层

教师在设计课后作业时要充分结合学情,既要设计一些能让大多数学生“吃得了”的基础题,也要设计一些能让少数学生“吃得饱”的拔高题,这样既实现了巩固“双基”的目的,又让学生有所提高.通过“由浅入深”的设计来提高学生的思维水平,遵循“最近发展区”理论,让学生的学习能力梯度提升.

2 搜集整理,科学整合

作业的评讲不能用简单的对错来衡量,过于简单、机械的评讲难以让学生获得有价值的信息,因此,教师要善于收集、整理作业信息,经过分析和整合充分发挥作业的价值.同时,要注意错因的分析和归纳,在教学中有针对性地进行巩固训练,帮助学生走出误区,提升解题质量.

(1)搜集方法

受学生不同知识水平和不同思维方式的影响,在作业中常会出现“一题多解”的现象.对于那些浅显易懂的具有一定创新精神的解题方法,教师要做好记录,在适当的时机引入课堂,以此丰富解题思路,提升学生思维水平和解题效率.

这是复习乘法公式中的一道练习题,主要应用立方和公式求解,公式的内容学生已熟练掌握,但灵活运用水平还有待提高,为此,教师设计了这道题帮助学生巩固和强化公式的理解和应用.

预设解题方案:

由a+b+c=0,可得a+b=-c,b+c=-a,a+c=-b.

又a3+b3=(a+b)[(a+b)2-3ab]=-c(c2-3ab)=-c3+3abc,所以a3+b3+c3=3abc.

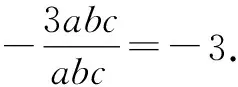
这是一种常规的方法,根据课堂复习内容容易联想应用立方和公式求解,故借助通分一步步挖掘已知和所求式子间的联系,从而通过转化将所求式子化简,最终求解.该方法较容易理解,也比较容易上手,故应用此方法解题的学生也较多,但在作业解答中也惊喜地发现了其他解决方案.

新方法:

由a+b+c=0,可得a+b=-c,b+c=-a,a+c=-b,所以

显然较预设解题方案相比,新方法更为简单,运算量更小.解题时之所以大多学生选择了预设解题方案,主要是因为学生在解题时基于课堂复习内容进行联想,故将其转化为立方和的形式,虽然达到了预期目标,但仔细分析不难发现学生的数学思维出现了局限性.因此,为了打破这种局限,教师要及时整理并记录,在作业评讲时充分利用好这些简单易懂、新颖独特的解题方法,培养学生思维的开放性和灵活性.

(2)搜集错误

作业解答中不仅会出现很多新想法和新思路,也会出现各种各样的错误,因此,教师不仅要做好解题方法的搜集,更要关注学生的错误.错误是学生对知识掌握情况的最直接反馈,若想让学生有所提升就需应用好这些错误资源,通过收集和整理易错题,及时帮助学生找到错因,并指导学生进行针对性的练习,从而有效避免错误再次发生,提高解题准确率.

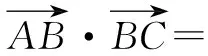
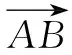
这样细心的整理和总结,便于教师更好地了解学情,为后期教学计划的制定及作业的布置提供重要依据,是不可或缺的教学资源.

3 激励评价,适度引导

课堂时间有限,教师很难面面俱到地照顾每个学生的想法,因此,要利用好作业,发挥其桥梁作用,为师生建立起有效沟通的平台,让教师可以更加直接地了解学生、指导学生,从而促进学生共同进步.同时,在批改作业时,尽量避免简单的“勾叉”批改法,可以写一些反馈意见,多一些鼓励评价,从而使作业批改更具人情味,更能激发学生学习信心[3].例如,面对独特的见解要给予鼓励,让学生收获成功的喜悦;面对错误,在鼓励的同时给予正确的引导,让学生既能及时订正,又不会丧失学习信心.总之,要善于发现学生的闪光点,让学生在成功的体验中收获学习的信心,进而促进学习成绩和学习能力梯度上升.

例3求函数y=-cos2x+4cosx-3的最值.

本题求解时部分学生给出了这样的步骤:

令t=cosx,则函数变为y=-t2+4t-3=-(t-2)2+1.故最大值为1,无最小值.

显然,利用换元法求最值,其整体解题思路没有问题,但换元时学生忽视了t的取值范围.事实上,本题中-1≤t≤1,故正确的答案为ymax=0,ymin=-8.

针对本题的作业评价,教师首先要肯定学生的解题思路,接下来提醒学生注意函数的定义域,有条件的情况下可以给出相似练习让学生进行巩固.这样,通过作业反馈既达到了激励的作用,又强化了学生对易错点的理解.相信这样的指导一定会让学生有所收获,有所提高.

总之,教师在作业设计时不要贪多、贪难,要切实从学生实际出发,通过精心设计、搜集信息、激励评价来提升学生作业质量,进而培养学生良好的作业习惯,促进学习能力不断提升.