提升高中学生数学运算能力的实践探究*

⦿ 广州市第五中学 邢 燕

1 高中数学教与学中常见的运算问题

1.1 学生学习各类运算方法时常见的问题

一些学生在数学学习中对运算不够重视,平时学习和练习中只强化思路训练,不重视运算训练,认为算错只是大意,只要注意就能避免,殊不知运算也是讲技巧和方法的,正确的运算方法可以帮助你算得又快又准,错误的运算会导致你总是掉坑.一些学生在数学学习中对运算不够认真,出现看错数、算错数、计算不严谨等现象,导致最终答案错误.这样的运算错误大部分学生是归为粗心,自认为这题我会,只是不小心算错而已,下次小心就可以了.但事实上,数学运算是数学学科的核心素养之一,数学的学习就是要培养学生认真细致的做事态度,避免“差之毫厘,谬以千里”.

1.2 教师教学各类运算方法时常见的问题

首先,有些教师在教学过程中比较重视概念、定义等知识点的教学,强调通过概念、定义掌握问题的本质,常忽略了概念、定义的掌握也需要练习来强化.而数学练习中大多需要运算,只有运算正确才能得到正确答案.其次,教师在教学中往往会重视提问的设计,分析解题思路,但会忽略解题过程中的运算方法和运算步骤的总结与归纳.最后,教师在教学中虽然强调了正确的运算过程,但忽略了对学生易错点的分析,导致学生总是会而不对,不能通过练习获得成就感,从而对数学产生厌倦心理,对数学学习失去兴趣.

2 提升高中学生数学运算能力的策略

2.1 理解概念,夯实运算根基

利用新授课帮助学生理解不同的运算有不同的法则,但又有相通的体系.高中阶段常用的数学运算有整式、分式、根式的运算,指对数的运算,复数、向量的运算,集合运算,三角恒等变形,立体几何体积、表面积、角和距离的运算,排列组合与概率统计的运算,导数与函数、数列的运算,等等.可以说,数学学习离不开运算,但运算前一定要深入理解知识的来龙去脉,熟练掌握概念、定理、公式.教师要引导学生将新学的概念与旧知识进行比较,以加深理解,并巩固复习.只有正确理解概念,在运算中才能注意到平方会增根、约分会漏解、对数函数要注意定义域等这些细节,才能在运算中保持恒等变换.所谓运算的基本知识和方法,就是明确每种运算所适用的对象和范围,理解这种运算的数形关系,熟悉其逆用、变式及推广.在教学中,教师要给出针对性的训练,以加深学生对概念的理解.例如,“三角函数恒等变换”中“二倍角公式”这一节的新课教学,推导出公式,简单直接运用后,就需要进行公式的逆用、变形训练.

例1求下列各式的值:

(4)cos 20°·cos 40°·cos 80°.

教师可根据基本概念、基本公式设计一些题目变式,以问题串形式给出,激发学生的思维和兴趣,鼓励他们解决复杂问题提升数学运算能力.这样可以加深学生对公式的理解记忆,熟悉公式的不同形式,更好地运用二倍角公式解决有关倍角、半角的问题,提高运算的正确率.

2.2 优化方法,明确运算方向

教师在教学中要展示不同的解题方法,让学生体会不同方法的运算差异.对运算过程中受挫的学生,教师应及时帮助他们发现和纠正错误,鼓励并指导他们反思总结,改进方法,明确运算方向.同时,为学生提供多样化的训练,包括不同难度和题型的题目,以帮助学生熟悉各种类型的数学运算,培养他们的运算能力.例如,求解圆锥曲线中的最值问题,不仅需要运算的基本功,还需要选择合适的方法,才能简化运算,正确求解.

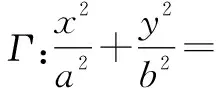
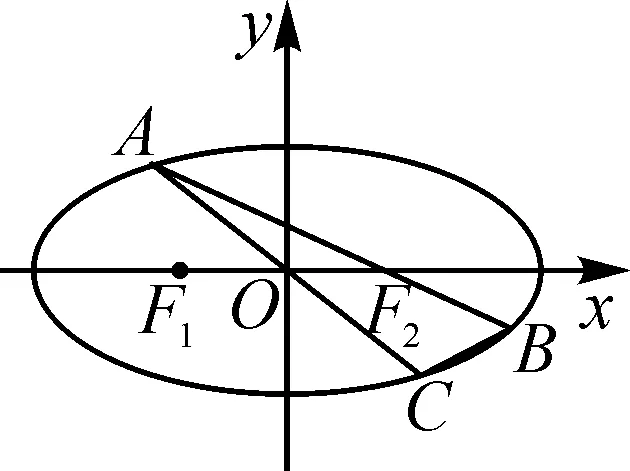
图1

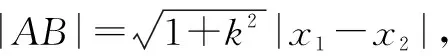
不同背景的题目往往几个方法都可以解决问题,但不同方法解决问题的难度是不同的,有些简单直接,有些则比较繁琐,这就需要优化解题策略,选择合适的运算方法.总之,在教学中要教会学生明确运算方向,选择合适的方法,促进运算能力的提高.

2.3 养成习惯,熟用运算方法

教学中可利用专项训练提高学生的运算能力,促使学生熟练掌握运算方法,养成习惯.专项训练也称为题组训练,该训练不是盲目的,而是有目的、有计划地进行各个运算专题的训练.明确的目标可以有效引导学生的学习,不做无用功,少走弯路,使学生在训练中学会运算的通性通法,达到触类旁通的效果.这种训练不能搞题海战术,需要教师精挑细选有变式、有梯度的同类题.认真研究高考真题,参考各地模拟题,可以直接归类练习,还可以变换数字、角度进行变式训练.通过对这类高质量题的反复练习,归纳总结,纠错反思,有效提高学习效率的同时,也提高了针对这类题的运算能力.学生在这样的专题训练中,可以熟练掌握一类题的运算方法,形成“肌肉记忆”,即养成习惯.在复习课中使用这种训练方法效率高,效果好.例如,在高三一轮复习中,讲解“直线与圆相切”这一节时,有关切线长的最值问题,可以给出以下例题和变式.

例3若P为直线y=x+1上一动点,过点P作圆C:(x-3)2+y2=1的切线PA,A为切点,求切线长的最小值.

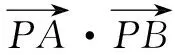
高考链接(2020年新课标Ⅰ卷·理)已知⊙M:x2+y2-2x-2y-2=0,直线l:2x+y+2=0,P为l上的动点.过点P作⊙M的切线PA,PB,切点为A,B,当|PM|·|AB|最小时,直线AB方程为______.

深度的变式和高考链接,使学生熟悉这类题目的题设和所求以及解决这类问题的通性通法,再遇到此类问题时能快速找到最简单的解题路径,从而提高学习效率,对学生的数学思维和数学运算能力都能起到综合提升的效果.

3 反思总结

两年的实践探究,我们发现提升数学运算能力对不同的学生而言有很大的差异,个体的主观能动性对效果影响极大,唯有持之以恒方有成效.教师需要把数学运算的培养贯穿教学的始终,在教学中可以运算作为纽带建构教学进程,引导学生通过运算发现规律,借助运算解决问题[1],发展学生的数学思维,促进高中学生运算思想和运算能力的形成.数学运算核心素养的形成,不仅需要教师的指引,更需要学生的积极参与,以形成自己的运算习惯和运算观.数学运算核心素养的培养是一个循序渐进的过程[2],需要一线教师长期不懈怠的探索和研究.因此,应把数学运算核心素养的培养渗透到每一节课的教学中,落到实处.