巧用导数定义求解一类含参问题*

⦿ 福建省同安第一中学 范丹妮

1 引言

函数与导数是高中数学的重要内容之一,对函数与导数的学习与研究,能培养学生数学抽象、逻辑推理、数学运算、直观想象等核心素养,同时也向学生渗透方程与函数、化归与转化、分类讨论、数形结合等重要的数学思想.纵观近几年的高考数学试题,压轴题通常是考查函数与导数,而且含有参数的题型更是热点[1],这类问题综合性强、难度高,学生不易掌握.目前,解决含有参数问题的常见方法主要有分类讨论法、分离参数法、数形结合法等[2].根据笔者平时教学工作中的观察发现,学生对于含参数问题的讨论常常找不到分类的标准,无从下手,或者是分类重复、缺漏,导致失分,故解这类题时学生往往更喜欢选择分离参数法,然而该法在解题中有时也会碰到一些问题.本文旨在通过典型例题的对比解析,以期为学生在遇到相关的含参问题时提供解题思路参考.

2 典例解析

例1已知函数f(x)=lnx+a(x-1)2(a∈R),当x≥1时,f(x)≥a(x2-1)-ex+e恒成立,求a的取值范围.

解法1:分离参数法.

当x≥1时,f(x)≥a(x2-1)-ex+e恒成立,即x≥1时,2a(x-1)≤lnx+ex-e恒成立.

①当x=1时,0≤0显然成立.

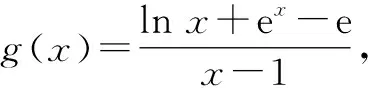
对g(x)求导,得

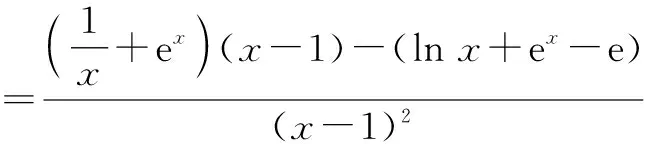
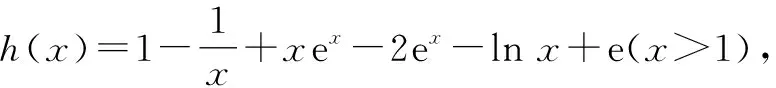
解法2:分类讨论法.

由题意得,当x≥1时,lnx+ex-2ax+2a-e≥0恒成立.

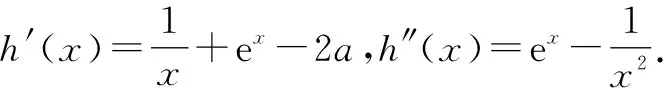
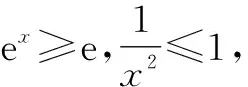
故h′(x)≥h′(1)=1+e-2a.

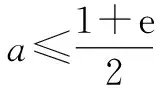
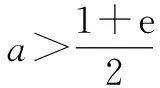
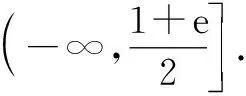
点评:该方法条理清晰,分类不重不漏,讨论有理有据,但实际情况是让学生给出这样的解答并不容易.对于高三第一轮复习中的学生来说,当一次求导不能解决问题,尚能想到二次求导,而该题的难点在于求导之后对参数的分类讨论.

解法3:导数定义法.

由解法1可知g(x)在(1,+∞)上单调递增.

点评:在解法1的基础上分离参数后,具有导数定义式特征的函数,如果最值点取不到,可以巧用导数的定义和几何意义求出极限值.

例2(2017年全国卷Ⅱ)已知f(x)=ax2-ax-xlnx,且f(x)≥0.求a的值.

解法1:分离参数法+导数定义法.

f(x)的定义域为(0,+∞).由题意,知f(x)=ax2-ax-xlnx≥0,即a(x-1)≥lnx.

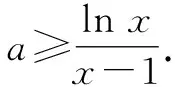
②当x=1时,0≥0显然成立.

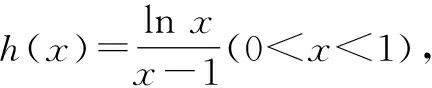
令g(x)=x-1-xlnx,则g′(x)=1-lnx-1=-lnx.当00,g(x)单调递增;当x>1时,g′(x)<0,g(x)单调递减.所以g(x)max=g(1)=0,故g(x)≤0恒成立,从而h(x)在(0,1)上单调递减.然而x=1时,h(x)的分母无意义.

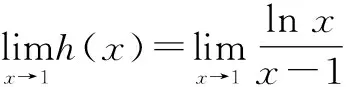
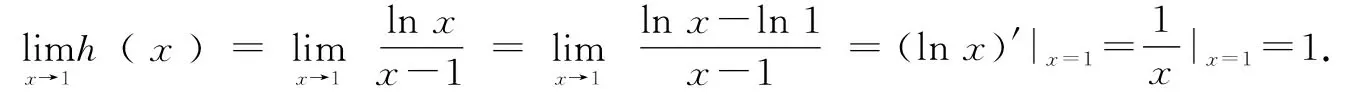
综上可知,a=1.

点评:导数的定义和几何意义在求解极限时具有独特的不可替代的作用,给原本看似走到绝境的解答迎来了柳暗花明.有些问题并非只能借助高等数学的洛必达法则.该解法巧妙地回归了课本导数的概念及其几何意义,避开了洛必达法则.实用性在于分离参数时若出现分母分子均为0的形式,我们又多了一条解决策略.

3 结语

学无止境,数学的世界更是充满了无限的奥妙,关于利用导数定义解决含参问题还有待深入研究.数学含参问题变化多端,需要灵活多变地采取应对策略,这就需要我们平时注重培养数学思维,以及剖析关键问题、灵活转化问题的能力,以便在遇到含参问题时能更高效地解题.