改进灰狼优化算法在特征栅格地图上的路径规划

音凌一，向凤红，毛剑琳

（昆明理工大学 信息工程与自动化学院，昆明 650500）

移动机器人路径规划是指：在给定的环境中，根据指定的评价标准规划出一条从起点到目标点的可行路径，并保证移动机器人在不会碰撞到障碍物的前提下，尽可能优化路径[1]。

随着移动机器人应用场景的不断拓展，对移动机器人路径规划的要求越来越高，越来越多的研究学者开始在路径规划的问题研究上，使用群智能算法。如蚁群算法（ACO）[2]、粒子群算法（PSO）[3]和萤火虫算法（FA）[4]等。

灰狼优化算法（Grey wolf optimizer，GWO）是2014 年由澳大利亚学者Mirjalili 等提出的一种群智能优化算法[5]。该算法是通过模拟灰狼种群的等级制度和捕猎行为，来实现优化搜索的目的，具有原理简单、参数少、易于实现和有较强的全局搜索能力等特点。已经被证明在函数优化方面，在求解精度和收敛性上要明显优于粒子群优化、引力搜索算法（GSA）[6]、差分进化算法（DE）[7]和遗传算法[8]的结果。目前灰狼优化算法已经在调度问题[9]、求解约束优化问题[10]、高维优化问题[11]和路径规划问题等方面得到成功的应用。但是，GWO 算法和其它的群智能算法相似，也存在着求解精度低，收敛速度慢和易陷入局部最优的问题。同时应用在路径规划上，出现了易陷入局部最优和效率低的问题。为克服这些问题，研究学者们提出了各种改进方法。

Long 等[12]提出一种基于对数函数的非线性衰减参数a，将参数a改进成先快后慢的非线性衰减，增加了算法局部搜索的时间，但这种非线性衰减方式，减少了全局搜索的时间；滕志军等[13]受到PSO算法的启发，将个体的历史最佳位置引入到灰狼的位置更新公式中，同时采用二次函数，将线性衰减参数a改进成先慢后快的非线性衰减；魏政磊等[14]利用α狼、β狼和δ狼的适应度值，基于与适应度值成正比的概率分布，改进了位置更新公式，但忽略了算法在求解最大值问题时，α狼的占比会变成最小的情况；刘二辉等[15]根据路径规划的具体问题，引入了路径微调算子和邻域变异算子，有效的提高了算法在路径规划问题上的性能，但这种改进的算法只针对路径规划问题，无法适用于解决其他问题；Zhang 等[16]根据灰狼之间的最大距离和平均距离，设置距离变化率，引入动态权重，改进了位置更新公式，并把改进后的算法成功的应用在三维路径规划问题上，但并没处理算法应用在路径规划上效率低的问题。赵江等[17]提出了特征栅格的概念，并通过仿真实验，证明特征栅格地图，可以有效的加快群智能算法在路径规划问题上的求解速度，但设置的特征栅格提取规则和邻接矩阵的建立都太过繁琐。

基于以上研究，本文提出了一种改进灰狼优化算法（Improved gray wolf,IGWO）在特征栅格地图上的路径规划方法。先对灰狼算法进行改进，引入调节因子来控制参数a的衰减，又引入动态权重和游走策略提高算法的性能；之后提出了判断特征栅格的新方法，加快了特征栅格地图的建立；同时为简化邻接矩阵的建立，提出了远距离栅格和可视步长。

1 灰狼优化算法的改进

灰狼是位于生物界食物链顶端的动物。一般是群居生活，种群内分为4 个等级：第一级是α狼，是领导整个种群的个体；第二级是β狼，主要是辅助α狼进行决策；第三级是δ狼，执行侦查和放哨等任务；第四级是ω狼，是最底层的灰狼，服从前三级狼的指挥。灰狼优化算法就是对灰狼种群按等级制度进行捕猎行为的数学模拟，其数学描述为

1）包围猎物

式中：t为当前的迭代次数；A和C为协同向量系数；XP（t）为猎物位置；X为灰狼的位置向量。

向量A和C的计算公式为：

式中：a为在迭代过程中从2 线性减少到0；r1和r2是[0,1]中的随机向量。

2）狩猎

式中：Xα、Xβ和Xδ分别为最优解、次优解和第三优解的位置；Dα、Dβ和Dδ分别为灰狼个体到α狼、β狼和δ狼的距离。

3）搜寻和攻击猎物

灰狼群体主要根据α狼、β狼和δ狼的信息来进行捕猎，在数学描述中主要根据A向量来控制灰狼是搜寻猎物还是攻击猎物。当|A|＜1 时，强迫灰狼攻击猎物；当|A|＞1 时，迫使灰狼远离猎物，扩大搜索范围，去寻找下一个猎物

1.1 可调节非线性收敛因子

由前述可知，在灰狼优化算法中调节算法全局搜索和局部搜索的平衡主要是由参数A决定的，从式（3）可以看出，参数A的变化由a决定。对于不同的实际情况，对算法是更倾向于全局搜索还是更倾向于局部搜索的要求是不同，如果只是将收敛因子a简单地改进成非线性衰减，不符合实际要求的。为了达到根据具体要求对a的衰减进行调节的目的，本文提出了一种基于调节因子n的可调节非线性收敛因子。根据算法应用情况的不同，调节n的大小，使a以不同的衰减方式进行衰减。

式中：t为当前迭代次数；tm为最大迭代次数。

图1 所示的是当t=1 000 时，不同取值n对a衰减的影响，可以明显看出当n的取值不同时，a的衰减方式也是不同的。当n取值越小时，a的值在迭代中会越早达到1，即A的值达到1 的时间也会越早，算法在局部搜索的时间会加长；当n取值越大时，a的值在迭代中会越迟达到1，即A的值达到1 的时间也会越迟，算法在全局搜索的时间会加长。同时不管n的取值是多少时，a都是非线性衰减。

图1 收敛因子对比图Fig.1 Convergence factor comparison

1.2 动态权重

标准灰狼算法中灰狼种群中，个体进行位置更新是根据α狼、β狼和δ狼的位置进行更新的，3 只狼起着一样的作用，并没有体现出α狼是最优狼的重要性，这种平均作用，会使算法的整体收敛速度变慢。为加快算法的整体收敛速度，本文提出一种基于适应度变化的动态权重，在迭代中加大优秀狼的作用，减少较差狼的作用。

式中：fα、fβ和fδ分别为α狼、β狼和δ狼的适应度值。

根据式（8）可改写为

1.3 游走策略

式（10）和式（11）通过动态权重，加大了迭代过程中优秀狼的作用，但这也减小了当α狼陷入局部最优时，算法逃离局部最优的能力。为了增强算法避免陷入局部最优的能力，提出了基于灰狼个体信息和最优信息的游走策略。

基于个体信息的游走，则

基于最优信息的游走，则

式中：i和j为种群中随机的两个不同的个体；rand 为（-1,1）之间的随机数；o 为种群中最优的个体。

1.4 改进算法的具体步骤

改进后算法的具体步骤如下：

步骤1 根据不同问题的需求，确定调节因子n的大小。

步骤2 初始化灰狼种群，设置种群大小N、最大迭代tmax。

步骤3 计算每个灰狼个体的适应度，确定α狼，β狼和δ狼。

步骤4 计算参数a、A及C。

步骤5 根据式（11）更新灰狼个体。

步骤8 是否达到最大迭代次数。是，输出最优个体和最优个体适应度值；否，进行步骤4。

2 改进特征栅格地图

2.1 特殊栅格的确定

文献[17]提出了特征栅格的概念，通过对栅格地图中特征栅格的提取，简化栅格地图，以达到加快搜索速度，优化搜索路径的目的。具体是通过蒙特卡罗模拟，总结出12 种可以组成任何障碍物的基本形状障碍栅格，在确定这12 种基本形状栅格的特征栅格位置。如果要确定地图中具体特征栅格的所在位置，首先确认栅格地图中障碍栅格是由哪几种基本形状组成后，之后才能确认特征栅格的所在位置，通过这种方法来确认特征栅格的位置，太过于繁琐。本文基于特殊栅格的概念提出了一种只用通过探索每个栅格周围9 邻域栅格的障碍物是否存在，来确认该栅格是否为特殊栅格的方法。

1）判断栅格是否是障碍栅格，设机器人a所在的位置为（i,j），即（i,j）不能是障碍栅格。

2）判断栅格是否在障碍物的顶角。（i+1,j+1）、（i+1,j-1）、（i-1,j+1）和（i-1,j-1）中，至少有一个栅格存在着障碍物，也就是图2 中黑色区域位置。

图2 特征栅格的判定Fig.2 Determination of characteristic grids

3）判断栅格的连通性是否完好。（i+1,j）、（i-1,j）、（i,j+1）和（i,j-1）中，至少有两个栅格中没有障碍物，也就是图2 中红色区域位置。

4）满足1）～3）条件的栅格即为特征栅格。

此方法只需要对栅格周围的9 邻域栅格进行简单的判断，就能准确快速的确认栅格是否为特征栅格。建立20×20 的栅格地图，利用本文提出的判断特征栅格的方法，对栅格地图中的栅格进行判断并提取，其中提取出的特征栅格用蓝色的“+”标记出来，如图3 所示。

图3 提取特征栅格Fig.3 Extraction of feature grids

2.2 远距离特征栅格

对于大多数的路径规划问题来说，最短的路径都是产生在起点与终点的连线附近。基于这种思想，本文设立了距离限制D，判断特征栅格与起点和终点连线线段的距离，去掉与起点和终点连线线段距离过远的特征栅格。

式中：（a1，b1）为起点坐标；（a2，b2）为终点坐标；（i，j）为特征栅格点的坐标。当a1=a2，即起点和终点在一条纵轴上，距离为|i-a1|。

具体的距离限制D的大小，要根据地图的实际情况设置。设置D的大小后，对所有特征栅格进行判断，满足dij＞D的特征栅格全部认为是远距离特征栅格。设置D=6，起点为（1,1），终点为（20,20），去除特征栅格中的远距离特征栅格，处理过后的特征栅格地图如图4a）所示；设置D=10，起点为（1,1），终点为（1,20），除去特征栅格中的远距离特征栅格，处理过后的特征栅格地图如图4b）所示。其中红色的“+”号是除去的远距离栅格，可以明显看出特征栅格减少了许多。

图4 远距离栅格的去除Fig.4 Removal of distant grids

2.3 设置可视步长

确定特征栅格后，因为特征栅格之间的连通性并不能保证，所以要对所有的特征栅格进行可视性判断。图4a）虽然对20×20 的栅格地图已经进行了特征栅格的提取和对远距离特征栅格的去除，但是保留下来的特征栅格仍然还有60 个，如果对所有的特征栅格点进行可视性判断，将要进行次。但是当两个特征栅格的相隔距离过长时，它们之间可视的概率也会降低，可视性判断大部分都是不可视的。为此设置可视步长L，用来减少特征栅格之间可视性判断的次数和提高建立邻接矩阵的速度。设特征栅格点的坐标为（i,j），即最远只会对（i+L,j+L）,（i+L,j-L）,（i-L,j+L）和（i-L,j+L）这4 个栅格点进行可视性判断。虽然这样构成的邻接矩阵还是60×60 的，但是减少了可视性判断的次数，同时也简化了邻接矩阵构成。

如图5 所示，设A点的坐标为（i，j），可视步长为L=2。对A点进行可视性的判断，即A点的可视范围最远（i+2,j+2）,（i+2,j-2）,（i-2,j+2）和（i-2,j-2），i为红色标记的栅格。

图5 可视性判断Fig.5 Visibility determination

1）两个特征栅格之间的连线不经过障碍物，如图中A栅格和B栅格的情况，判断特征栅格可视，路径L1可以行走。

2）两个特征栅格之间的连线不经过障碍物，但是与障碍物的顶点相切，因为是将机器人视为质点，且栅格都进行了膨胀处理，所以如图5 中A栅格和C栅格的情况，判断为特征栅格可视，路径L2可以行走。

3）两个特征栅格之间的连线经过障碍物，如图5中A栅格和D栅格的情况，判断特征栅格不可视，路径L3不可以行走。

4）两个特征栅格超出了可视范围，如图中A栅格和E栅格的情况，判断特征栅格不可视，路径L4不可行走。

通过以上4 点判断可以快速的确认特征栅格之间的可视性，建立所对应的邻接矩阵。

3 实验仿真

3.1 标准测试函数实验仿真

为证明改进算法的性能，本文使用单峰函数、多峰函数和固定多峰函数3 种具有不同特点的标准测试函数测试改进算法的有效性，表1 给出了具体的标准测试函数。此次仿真实验为避免单次仿真实验结果的偶然性，会进行50 次重复实验，计算仿真结果的标准差和平均值，用平均值来表示算法的精度，用标准差来表示算法稳定性。在与GWO 算法、PSOGWO 算法[13]和EGWO 算法[18]进行比较。在仿真中，IGWO1 算法和IGWO2 算法是采用本文所提出可调节收敛因子的方法进行改进的算法,只不过调节因子n的大小不同，IGWO3 算法是采用本文所提出的可调节收敛因子和动态权重的方法进行改进的算法。

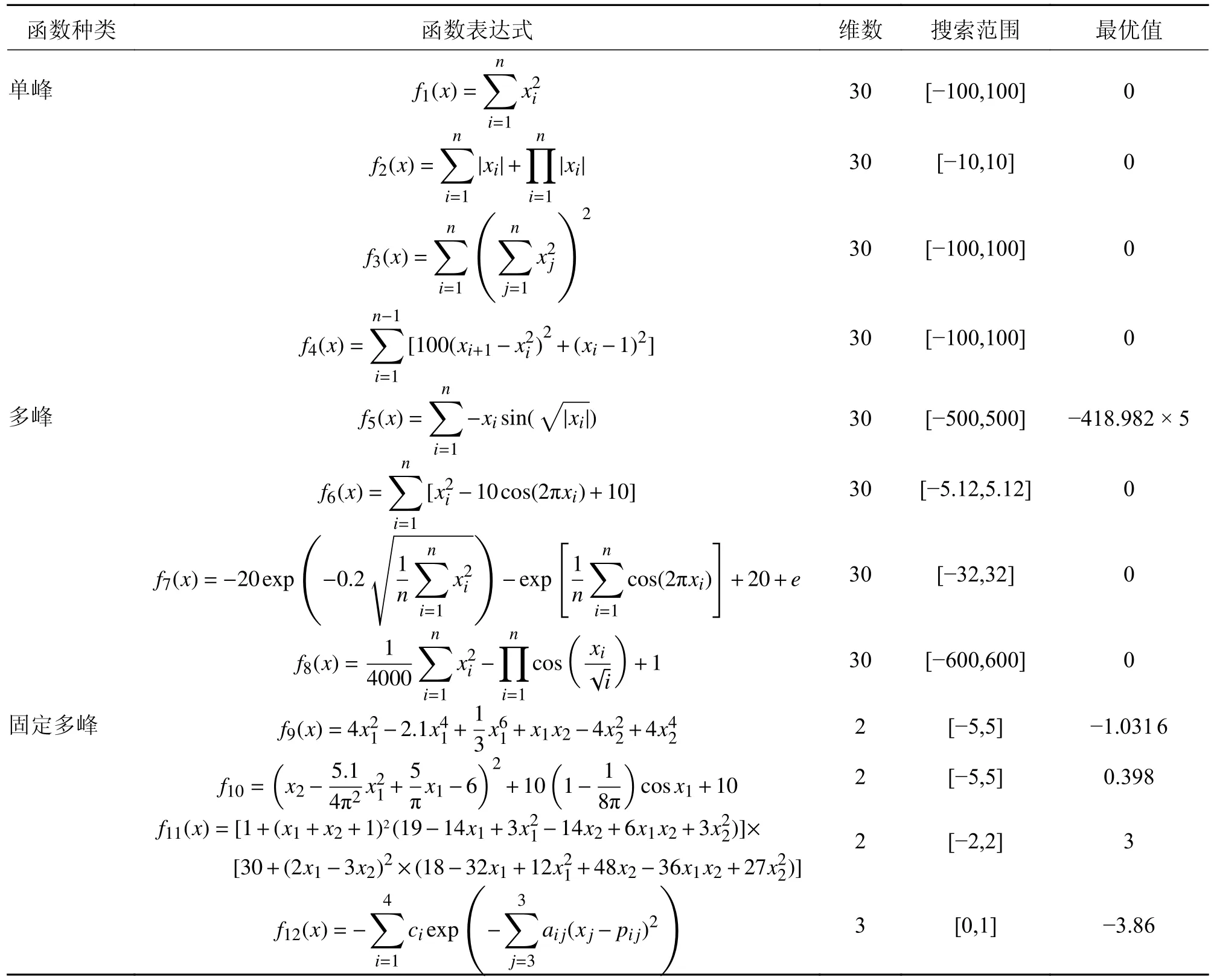
表1 标准测试函数Tab.1 Standard test functions

本次仿真实验的参数设置，最大迭代次数tmax=1 000、种群大小N=30；PSOGWO 算法中学习因子c1=c2=2；IGWO1 算法、IGWO3 算法和IGWO 中调节因子为n=600；IGWO2 算法调节因子为n=800。

表2 为50 次仿真实验的平均值和标准差。由表2 明显可见IGWO 算法在单峰值函数f1～f3和多峰值函数f5～f8上表现较好，而IGWO1 算法在这些函数上表现较差，这说明动态权重和随机游走策略对算法的收敛精度和收敛速度有着正面的影响。而从固定多峰函数f9～f12上来看IGWO1 和IGWO2的改进效果要明显好于IGWO 和IGWO3 的效果。由式（15）可知，新的位置更新公式是根据α狼、β狼和δ狼的适应度值的绝对值大小占比来自适应的调整α狼、β狼和δ狼在灰狼位置更新公式中的占比，这个办法可以保证α狼在整个寻优的过程中所占的权重一直是最大的，有效加快算法的收敛精度和收敛速度，但是当α狼陷入局部最优时，根据公式α狼的占比依旧是最大的，这就会导致算法陷入局部最优，所以本文提出了游走策略，防止算法陷入局部最优。由IGWO3 算法和IGWO 算法在固定多峰函数f9～f12的对比可以看出，游走策略在避免局部最优问题上，具有较好的效果。

表2 标准测试函数仿真结果Tab.2 Simulation results for standard test functions

综上所述，在解决单峰和多峰函数时IGWO 具有更好的效果，在解决固定多峰函数时IGWO1 和IGWO2 的改进策略，具有更好的效果。

为进一步测试改进算法的性能，在单峰、多峰和固定多峰函数中各选出两个函数，分析收敛曲线，收敛曲线如图6 所示。从图6a）～图6d）中可以看出，相比其它算法，IGWO 算法和IGWO3 算法的收敛速度有着大幅度的提高，其中IGWO 算法的收敛速度更快，说明游走策略对收敛速度有一定积极的影响，但是影响不大。从图6c）～图6f）中可以看出算法IGWO 相比IGWO3 算法的收敛曲线多出许多折线，说明游走策略在α狼陷入局部最优时，可帮助算法逃离局部最优。对比IGWO1 算法和IGWO2算法的收敛曲线，会发现两种算法的收敛速度、收敛精度以及稳定性都是不一样的，说明调节因子n的改变会影响算法的性能。证明了根据实际问题，设置调节因子n，调节参数a的衰减方式的方法是有效的。

图6 收敛曲线Fig.6 Convergence curve

为验证算法在路径规划问题上的性能，下文将把IGWO 算法应用在栅格地图和改进的特征栅格地图上，来证明IGWO 算法在路径规划问题上的具体性能。

3.2 路径规划仿真实验

在路径规划问题中，灰狼个体储存的其实是一个一个的节点。这里的节点是整数，并不会存在小数，但是灰狼优化算法的位置更新公式和游走策略，会产生小数，所以在此次迭代中所有小数进行取整操作。同时在普通栅格地图中，游走策略可能会产生障碍物节点，当产生这样的节点时，用距离障碍物最近的一个非障碍物节点代替。

IGWO 算法在路径规划上的具体步骤：

步骤1 设置种群规模N，最大迭代次数tmax和变量的维数。

步骤2 初始化灰狼种群，随机产生灰狼个体（在特征栅格地图中灰狼个体储存的节点为特征栅格），对每个灰狼个体进行评估，看是否满足约束条件。

步骤3 计算每个灰狼个体的适应度，确定当前α狼，β狼和δ狼。

步骤4 计算参数a、A及C。

步骤5 根据式（11）更新灰狼个体。（取整操作）

步骤6 随机选取N/4 的灰狼个体，根据式（12）和式（13）操作）；

步骤7 计算3N/2 个灰狼个体的适应度，选取前N的作为新的种群，更新α狼，β狼和δ狼。

步骤8 是否达到最大迭代次数。是，输出最优个体和最优个体适应度值；否，进行步骤4。

在实验环境相同的情况下，建立20×20 和50×50 的普通栅格地图，再建立同等大小的特征栅格地图。分别用GA 算法、PSO 算法、GWO 算法和IGWO算法在不同地图上进行路径规划。其中设置初始种群N=30，最大迭代次数tmax=100，GA 算法中交叉概率为0.8，变异概率为0.1；PSO 算法中学习因子c1=c2=2，惯性权值ωini=0.9，ωend=0.4；IGWO 算法中调节因子n=600；20×20 的特征栅格地图中，距离限制D=5，可视步长L=5；50×50 的特征栅格地图中，距离限制D=15，可视步长L=10。

图7 和图8 是算法在20×20 和50×50 的栅格地图及特征栅格地图的仿真结果。从图7a）与图7b）和图8a）与图8b）中可以看出，IGWO 算法的路径明显更短，节点个数也更少。从图7c）与图7d）和图8c）与图8d）中看出，不管是在20×20 简单地图上，还是在50×50 复杂地图上，相比其它算法的收敛曲线，IGWO 算法的收敛曲线更优。IGWO 算法的曲线下降的更快，说明设置动态权重加大优秀狼的作用的改进是有效的，同时IWO 算法的曲线没有出现快速下降后陷入局部最优的情况，在迭代后期依然有着折线，说明了游走策略的有效性。

图7 20×20 路径规划结果Fig.7 20×20 path planning results

图8 50×50 路径规划结果Fig.8 50×50 path planning results

表3 是算法在栅格地图和特征栅格地图上，20 次仿真结果的平均值。从路径长度来看，相比于其它算法，IGWO 算法寻优的结果是最好的，节点个数也是最少的。在20×20 的普通栅格地图上，IGWO算法的路径长度，要比GA 算法、PSO 算法和GWO算法优化了3.93、2.91 和1.07。在50×50 的普通栅格地图上IGWO 算法的路径长度要比GA 算法、PSO 算法和GWO 算法优化了9.94、7.32 和4.19。说明对GWO 算法的改进，有效的改善了GWO 算法在求解路径规划易陷入局部最优的问题。

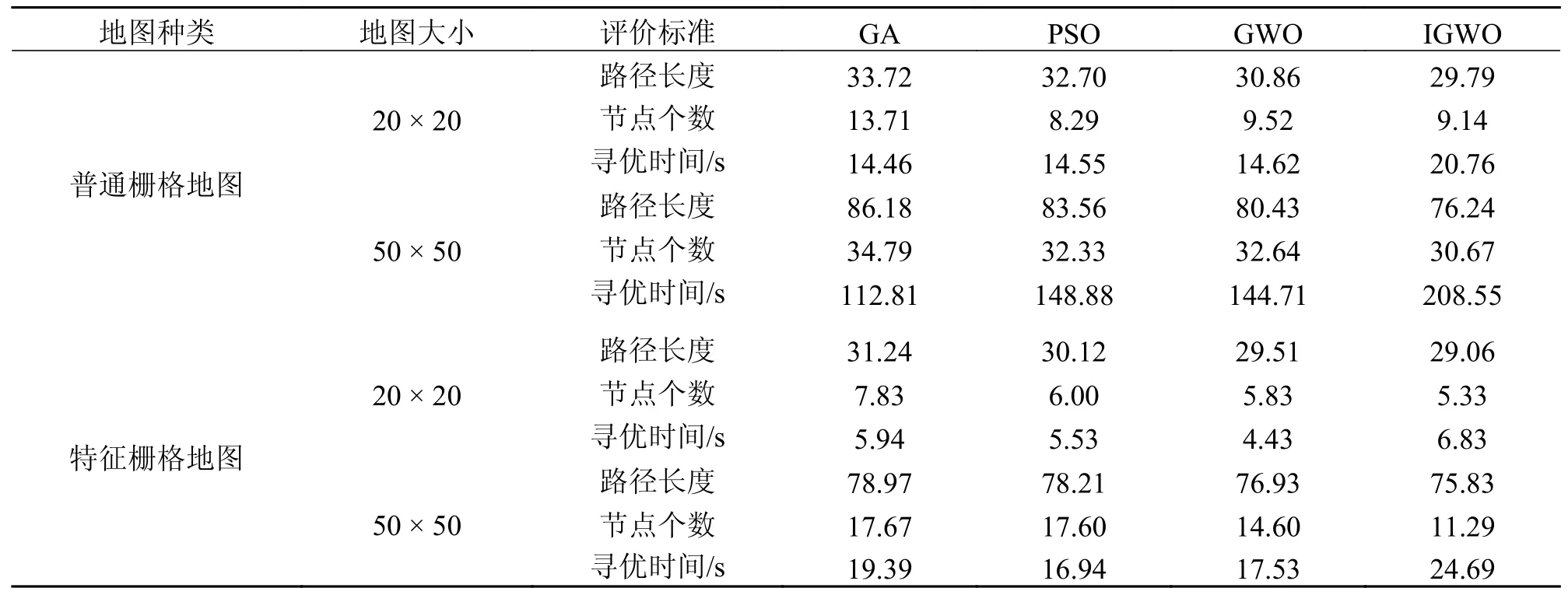
表3 20 次仿真平均结果Tab.3 Average results from 20 simulations

但是对比寻优时间，可以明显看出IGWO 算法的寻优时间较长，这是因为游走策略的设置，使算法变得复杂，降低了求解效率。为解决这一问题，建立特征栅格地图。对比特殊栅格地图和普通栅格地图的结果，可以明显看出，IGWO 算法在特征栅格地图上的寻优时间更短，节点更少。相比于普通栅格地图，IGWO 算法在20×20 的特征栅格地图上寻优时间优化了3.04 倍，节点个数减少了3.81；在50×50的特征栅格地图上寻优时间优化了8.12 倍，节点个数少了19.38。说明特征栅格地图的建立，有效的提高了IGWO 算法求解路径规划问题的效率。

3.3 与其它算法的对比

由于灰狼优化算法较为新颖，目前在二维路径规划上的相关文献较少，所以本文选择对比文献[19]改进的蚁群算法，来验证本文算法的有效性。蚁群算法的参数设置与文献[19]保持一致。特征栅格地图中的距离限制D=7，可视步长L=15。

图9 所示的是两种算法在30×30 地图上的路径规划结果。实际数据如表4 所示。本文算法对比文献[19]算法，路径的节点个数少了5，寻优时间优化了5.328 8 s，并且与障碍物顶点相切的点也减少了一半，极大地增加了路径规划的安全性。但从数据中可以发现最优路径长度相较于文献[19]增加了1.227 3，这是路径与障碍物顶点相切的点减少所导致的。

表4 30×30 地图实验结果对比Tab.4 Comparison of experimental results on 30×30 maps

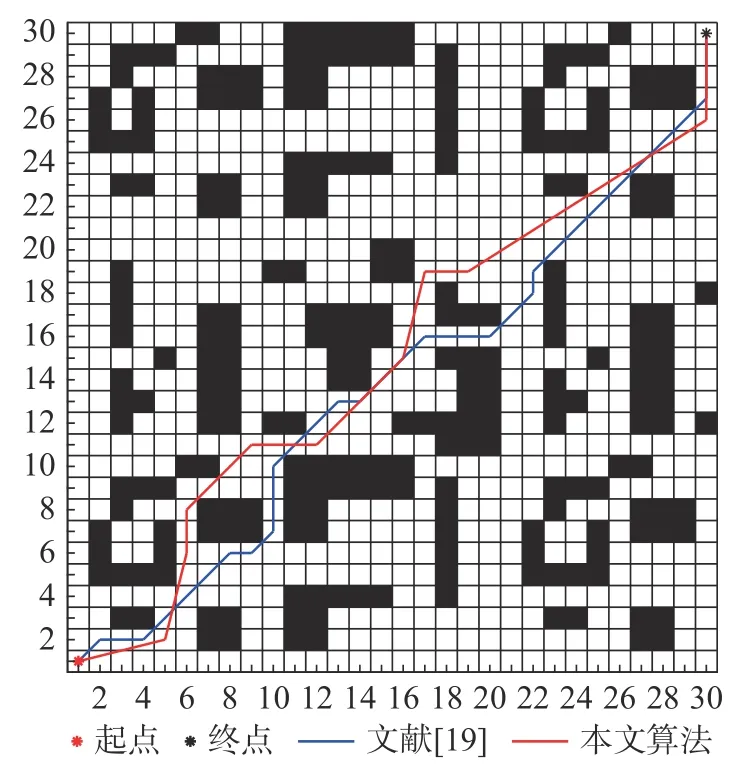
图9 30×30 路径规划结果Fig.9 30×30 path planning results

4 结论

提出一种改进灰狼优化算法在特征栅格地图上的路径规划方法。引入可调节收敛因子n根据实际情况调节全局搜索和局部搜索的平衡；为加大更新过程中α 狼的比重，引入动态权重，加快算法的收敛速度，同时使用游走策略减小因动态权重策略而导致的局部最优的概率；提出建立特征栅格的新方法，利用远距离栅格和可视步长的概念，加快特征特征栅格地图和邻接矩阵的建立；通过将特征栅格地图与改进灰狼优化算法结合，提高了灰狼优化算法初始种群的质量和求解路径规划问题的效率。标准测试函数的仿真实验证明IGWO 算法相对于其它算法，不管在收敛速度还是在收敛精度上都有着明显的优势，在固定多峰测试函数上也有较好的性能；路径规划仿真实验证明IGWO 算法在求解路径规划问题上能有效的避免局部最优；证明特征栅格地图能有效地提高IGWO 算法求解路径规划问题的效率。