基于GeoGebra 和GIF 图形的复变函数点集绘制

克拉玛依职业技术学院基础部 卢自娟 李闰祥

采用GeoGebra6 制作复变函数中的点集绘图，并解复数方程把复数根可视化，使学生通过简单的软件操作掌握抽象函数的几何意义。使用GeoGebra5 软件制作割圆术的GIF 图形，让抽象的内容更生动，提升课堂的可视化效果。

近年来，随着有关可视化教学的研究逐步开展，其在提升教学效果方面的作用日益受到重视[1]。而复变函数课程中研究不等式所确定的区域或非区域，连通或不连通，通过一个抽象表达式，一般很难判定。学生能通过手机版的GeoGebra6 软件自己操作，掌握抽象不等式所表示的图形，使得教师在这部分内容上处理简洁，达到事半功倍的效果。GeoGebra5 软件能导出GIF 图形，可插入到Word 文档、PPT、视频中，这里介绍割圆术与求函数极限的GIF 图形制作，让教师们的课堂更生动，达到更好的可视化效果。

1 运用GeoGebra 软件绘制复数域不等式确定的平面图形

几何思想贯穿整个复变函数内容，充分体现了《复变函数》是分析的几何化[2]，学习复变函数理论能让学生进一步领会代数与几何结合的神奇之处[3]。但复变函数课程中复数不等式点集究竟表示是怎样的平面图形，对学生来说却是一个难点，教师讲解完，学生通过死记硬背记住的内容如过山车一样很快会遗忘，其主要原因是对内容不理解，但通过手机上的GeoGebra 6 软件，学生能很快作出图形，观其形而知其义，从而达到所想要的学习效果，下面着重介绍点集绘图典型案例，达到窥一斑而知全貌的效果。

1.1 GeoGebra 6 软件复数输入的预备知识

GeoGebra 软件代数区输入的i均为虚数单位。在运算区输入虚数单位i时，可在快捷菜单中选择f(x)下拉菜单右侧的i，也可在电脑版键盘按Alt+i输入虚数单位。复数z在绘图或计算时都以z=x+iy转化，模的计算直接使用|...|，主辐角的计算直接在代数区输入arg(x+iy)。

在软件快捷菜ABC 输入&&就转变成了逻辑∧运算符，每个操作过程输入完按回车键，操作过程中//的内容为注释。

1.2 GeoGebra 6 软件绘制不等式点集

第一步，代数区输入:y＞tan(π/4)x∧y＜tan(π/3)x∧x2+y2＞1 ∧x2+y2＜9

案例1 圆及圆环相关的图形绘制。

（1）开圆环2＜|z|＜3

第二步，在代数区输入x2+y2＞1/9，/要转化成多项式，否则绘图区不显示图形/

得到如图5 所示的截取圆环区域，是单连通有界区域。

图2 圆外无界区域Fig.2 Unbounded area outside the circle

案例2 辐角主值的图形绘制。

第三步，代数区输入(x-1)2+y2＞(x+1)2+y2；/观测a=1时，区域是左半平面/

当所有车组号与车次按照最佳匹配结果一一对应时，取最小值0，此时车次与车组的匹配程度最高，车组运用最均衡。但在实际编配过程中，还需满足诸多约束，往往无法达到最小值，应尽量保证的取值接近最小值。

第四步，输入(x-1)2+y2＞a2((x+1)2+y2)；/先把第三步表达式前的图形按钮点击成为白色，即关掉图形，再输入第四步/

（2）π/4＜argz＜π/3，且1＜|z|＜3

图3 0＜a＜1 区域图Fig.3 0＜a＜1 area chart

高中阶段的学生思维异常活跃，并敢于提出不同的讲解与想法，特别是一些启发性的问题，他们是乐于思考并善于思考的。所以，在高中数学课堂教学中，新课程的导入期间，教师需为学生创设良好的问题情境，以让学生课前集中其全部注意力，并能开起其思维的闸门，让学生的求知欲和探知欲得到深化，进而能让学生的学习状态由原来的被动学习转为主动学习，进而能在和谐的学习氛围中进行数学知识的学习。

2017年6月，董明珠公开表示，银隆是“长期埋在沙漠里的金子”，有技术，只是缺管理和资金。而第三轮融资后，管理和资金银隆都不缺了，只要给她时间，可以“再造一个格力”。

在绘制辐角主值所在范围时，辐角所在的终边是一条过原点的射线，作图时处理成过原点的直线是argz＞α，就输入y＞tan(α)x。

第一步，代数区输入:y＞tan(-π/3)x∧y＜tan(π/3)x；/就可看到图形是一个无界的，位于第一与第二象限，夹在之间的部分，包括x 正半轴的无界连通开区域/

观察组患者的护理的满意率为100%,显著高于对照组的护理满意率。差异具有显著的统计学意义(p<0.05)。(如表3)

点击滑动条a后的按钮，绘图区就可以观察图形了。会发现当0＜a＜1 时，如图3 所示的0＜a＜1 区域，图形为:除去圆心在x正半轴上，位于右半平面上的圆外的区域，是连通无界的；当a＞1 时，如图4 所示的a＞1 区域，图形为圆心在x负半轴上，位于左半平面上的圆域，是连通有界的；a=1 是左半平面无界区域，单连通的。因滑动条停留在a=1 时，图形显示为一条线，因此，要通过第三步来观察，也可在GeoGebra 5 中输入上述步骤，再导出GIF 图，就可观察动态的图形效果。

在平面点集中通常要了解复数不等式所确定的范围是否是区域，并且要了解它的连通情况，这里通过几个典型案例让学生利用手机操作就可分析图形情况。

可得到如图2 所示的圆外无界区域，是复连通的。

图5 截取圆环区域Fig.5 Intercept the ring area

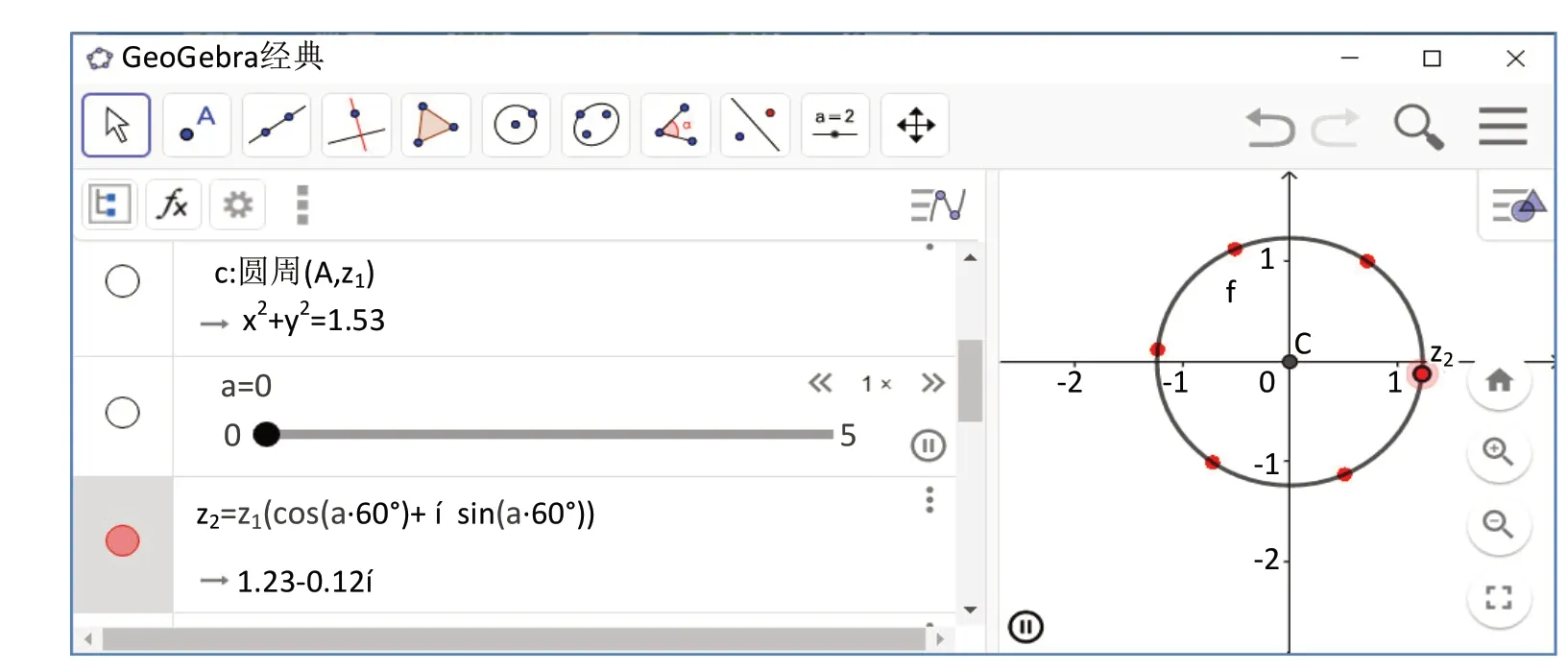
图6 复数方程根Fig.6 Complex equation roots

图7 圆内接正十边形Fig.7 The circle is inscribed with regular decagons

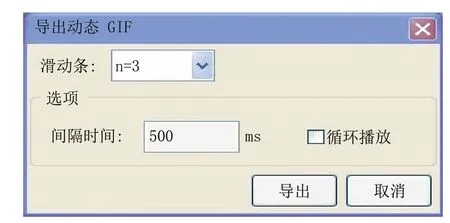
图8 GIF 导出图设置Fig.8 GIF export diagram settings

通过上面两个类型的介绍，关于复数域点集绘制图像基本都可掌握，需注意当所遇到的表达式不清楚是何种形式时可在运算区先化简，代数区输入表达式一般需去根号，才可绘制图形。

2 运用GeoGebra 制作GIF 图

Matlab、AutoCAD 等数学软件、绘图软件的功能强大，应用范围广，运用他们绘制的图形展示效果好，但对老师要求却很高，需要熟练掌握相应的计算机程序语言[2-5]。此外，使用这些软件制作课件，耗时多、效率低[6]，因此在这里介绍GeoGebra 6 书写操作过程形成GGB 文件，再由GeoGebra 5 导出GIF 图，提高教师制作动态课件的效率，提升课堂效果。

案例3 求解复数方程z6-3+2i=0，并把各解在复平面上表出。

2.1 GeoGebra 6 复数域解方程并绘图

(4)地层多重划分：地层多重划分方案请参照中国地层表(2014)最新标准。注意宇、界、系、统及宙、代、纪、世等的用法。

分析所用样品均采用随机取样的方法，所有试验组的各项指标均测定3次，利用Origin 9.0统计数据绘图和SPSS 17.0软件进行邓肯均数差异显著性分析。

2.2 GeoGebra 绘制正多边形

刘徽“割圆术”的思想无论是在数学课程的极限还是常数项级数的讲解中，一直是课程讲解的重要案例引入，教师在给学生阐述其思想时往往通过动画讲解，更能增强课堂的直观效果，激发学生的学习兴趣。

小学语文教学不应该只局限于课本上几篇简单的文章和诗歌，老师应该多鼓励学生们进行课外的阅读来辅助语文学习，只要是文字优美的符合小学生认知规律和能力都可以鼓励学生进行广泛阅读，通过课外阅读他们也可以体会到文字的魅力也可以有效地提升学生们的语感，间接性的提高学生们的口语表达能力，同时也能为以后学生的写作打下坚实的阅读和写作基础。

案例4 制作正n 边形的GIF 图。

GeoGebra 6 代数区输入

合理的水分和养分的施予对于葡萄生长是非常重要的。传统的浇灌过程，往往是使用大水漫灌或沟渠灌溉的方法，这种方式不仅受到地形的影响，操作过程中耗水量大，水资源利用效率低下。传统的施肥方式则是由人工直接施撒，这种方式很容易造成施肥不均匀，造成烧苗或肥力不足没效果，从而直接影响到植株的生长和葡萄的产量。水肥一体化技术由于其将肥料溶解到水中，从而避免了直接施肥不均匀的情况，同时节约了成本，也提高了葡萄的经济效益。

教师在讲解级数概念引入时，是通过在原有多边形的基础上增加三角形面积来实现，因此，上述过程可作如下更改：

第十步，在绘图区点右键，选绘图区，就可得到如图9 所示的正多边形叠加图，同理保存成ggb 文件，如：正多边形叠加图.ggb,在GeoGebra 5 中打开该文件，导出GIF 图即可，在常规菜单下换背景颜色为绿色，还可进行视频抠图。

图9 正多边形叠加图Fig.9 Regular polygon overlay

3 结语

总之，教学中运用GeoGebra 软件，便于让学生对所学的数学知识有更形象、更生动的理解，使繁琐的计算可以通过软件解决，增强了学生学习的兴趣以及解决问题的能力。