基于BP神经网络的斜拉桥车桥耦合振动响应预测

翟晓春

(山西省交通规划勘察设计院有限公司,山西 太原 030012)

0 引言

随着我国桥梁建设技术水平的快速发展和国民经济发展的迫切需要,桥梁结构逐渐向大跨、轻型、柔性方向的发展;车辆荷载的形式、轮重和行车速度不断提高,车辆与桥梁结构的动力相互作用越来越受到重视。相比静力荷载,车辆荷载作为动力荷载会使结构产生更大的响应,且动力时程与车、桥本身的动力特性、行车速度、路面粗糙度等众多因素有关。车辆造成的桥梁振动不仅决定了行车的舒适性,也影响到桥梁结构本身的安全性。因此,如何能够较精确地分析车桥耦合作用并有针对性地采取工程措施保证桥梁结构的安全和行车舒适性,是必须解决的重要问题。

国内外一些学者已经针对斜拉桥车桥耦合问题展开了研究。郭文华等[1]用多刚体模拟车辆、梁格法简化桥面板,以等效质量的形式施加二期恒载。李小珍等[2]采用空间杆系有限元模型,对芜湖长江大桥主桥在列车活载和公路活载下实际运营中的车桥动力响应进行了分析。Guo等[3]提出了一种集成任何车桥系统耦合的运动方程,通过直接积分法求解运动方程。王贵春等[4-5]利用有限元法和动力平衡原理分别建立了桥梁结构动力分析模型和车辆的多刚体动力学模型,还针对大跨度斜拉桥的几何非线性特征及铁路桥的特点,计算了斜拉桥的车桥耦合振动响应。李武生等[6]运用三角级数法将桥面不平顺模拟为具有各态历经的平稳随机过程,通过位移协调和力的平衡条件建立车桥耦合系统振动方程并用有限元分析软件ANSYS进行公路斜拉桥的车桥耦合计算。欧阳光[7]采用多刚体结构模拟车辆,空间杆系单元模拟桥梁,建立车桥耦合动力系统。Gao等[8]介绍了通用多尺度建模的原理和方法,基于Newmark-β法通过ANSYS和MATLAB软件编制了双轴车桥耦合振动分析通用程序。谢旭等[9]以跨度600～1 400 m的大跨度斜拉桥为对象,考虑拉索侧向振动影响,研究了钢索和CFRP索斜拉桥的交通振动响应。万信华等[10]研究了由于桥面不平整、车速对斜拉桥动力响应的影响。李江龙等[11]基于车辆动力响应的功率谱密度分析,对行车舒适性进行了评价。王凌波等[12]对不同体系斜拉桥车桥耦合共振效应进行研究,提出了斜拉桥车桥共振效应判定方法。Zhang等(2016)[13]探讨了风-车-桥系统耦合振动的机理,论证了平均风、波动风、抖振、轨道不平顺、轻轨车辆振动和桥梁刚度等基本因素的影响。

可见,既有研究已涵盖车桥耦合振动计算理论、分析方法和影响因素等,但车桥耦合分析工作量大,现有分析方法得到的结构响应不能显式表达,不便于工程应用。人工神经网络是一种机器学习算法,用于实现分类、聚类和预测等功能。当网络的拓扑结构合理、传递函数具有非线性功能,且网络经过适当训练,理论上神经网络可以逼近任意映射关系,这使得神经网络成为进行隐式显化的有效工具。因此,将神经网络技术应用于解决车桥耦合振动分析难以显式表达的问题是可能的。本文在分离式迭代法的基础上引入BP神经网络技术,通过学习、训练和验证,最终实现大跨径斜拉桥车桥耦合振动响应的准确预测。

1 BP神经网络技术

1.1 BP神经网络的结构和原理

BP神经网络的基本运算单元是神经元,BP神经网络由多个神经元组成,形成分布式的信息学习和处理机制。BP神经网络一般为多层神经网络,其中三层应用较多。输入层将刺激传递给隐藏层,隐藏层通过神经元之间联系的权重和传递规则将刺激传到输出层,输出层整理隐藏层处理的后的刺激输出结果。若有正确的结果,则将正确的结果和输出的结果进行比较,再逆推对神经网中进行反馈修正。BP网络能学习和存储大量的输入/输出模式映射关系,而无须事先知道这种映射关系的数学方程。

1.2 BP神经网络的建立和训练

BP神经网络的建立和应用可采用MATLAB神经网络工具箱。BP神经网络通常按下列步骤建立和训练:

(1)网络系统初始化。

(2)中间层输出,计算式为:

Hj=f(∑wijxi-aj),j=1,2,…m

(1)

式中:Hj——隐含层的输出值;

f(·)——激励函数;

m——节点数。

(3)输出层输出,计算式为:

Ok=∑HjWjk-bk,k=1,2,…l

(2)

式中:Ok——输出层输出结果;

l——节点数;

Wjk——权值。

(4)误差计算。

(5)更新权值和阈值。

(6)收敛判断,若不能收敛则返回步骤(2)重新计算。

2 车桥耦合振动理论

车桥耦合振动分析模型由车辆和桥梁两个动力学模型组成,车辆和桥梁通过桥面系相接触作为协调条件。桥梁结构车桥耦合动力学基本方程为:

(3)

式中:Mb、Cb、Kb——表示桥梁的质量、阻尼、刚度矩阵;

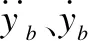
Fb——作用于桥梁上的车辆动荷载。

车辆可模拟为多自由度的弹簧、阻尼与质量体系,车辆系统运动方程应协调考虑路面粗糙度。

3 BP神经网络拟合车桥耦合的基本方法

采用神经网络技术拟合车桥耦合振动响应,需要通过准确的确定性结果对神经网络进行训练和学习,而训练的样本量越大则得到的结果越可靠。用于训练的样本值可通过精确的有限元分析得到,对于简单结构也可以通过解析方法得到。由于车桥耦合是动力行为,因此必须采用瞬态动力学分析,然后根据结构的特性,选取适宜的样本,并得到样本点的车桥耦合响应。进而将样本及其响应的动力响应作为样本进行训练。当神经网络训练完成后,就可以根据需要输入待考察的样本,从而通过神经网络得到待考察样本的动力响应值。具体流程如下:(1)建立结构有限元模型,计算结构的动力响应,并将准确的结果作为神经网络的输出参数;(2)根据结构动力特点,选取合适的样本作为输入参数;(3)建立BP神经网络模型,对样本进行训练、验证;(4)将待检测的样本输入神经网络,得到目标响应。

4 可靠性验证

采用一个单跨简支梁进行验证。简支梁计算跨径l=32 m;每延米质量为m=5.41×103kg/m,抗弯刚度为EI=3.5×1010N·m2。假设路面平整度好,假定路面粗糙度为满足零均值的平稳各态历经Gauss随机过程。采用一辆三轴车以60 km/h速度单向行驶,从前轴驶入桥跨到后轴驶离桥跨为分析过程。采用本文提出的神经网络方法得到的拟合结果与有限元分析结果的对比如图1所示。由图1可知,采用本文提出的神经网络计算出的车桥耦合振动影响与有限元结果吻合良好,证明该方法的可靠性。

图1 神经网络时程解与有限元时程解对比曲线图

5 工程案例

5.1 工程概况

某主跨1 088 m的双塔双索面斜拉桥,跨径布置为(100+100+300+1 088+300+100+100)m,结构对称。主梁采用扁平钢箱梁,上翼缘为正交异性板结构;桥塔采用钻石型钢筋混凝土结构;斜拉索采用高强度平行钢丝拉索,采用塔墩固结、塔梁分离的结构形式,采用半漂浮体系。该桥为双向六车道高速公路桥梁,设计汽车荷载为公路-Ⅰ级,设计车速为100 km/h。该斜拉桥总体立面布置如图2所示。

图2 斜拉桥立面布置图(cm)

5.2 有限元模型

采用梁单元Beam4建立主梁、桥墩、索塔模型,采用只受拉杆单元Link10单元模拟拉索,利用恩斯特公式修正拉索弹性模量考虑拉索垂度效应。桥梁结构有限元模型如图3所示。

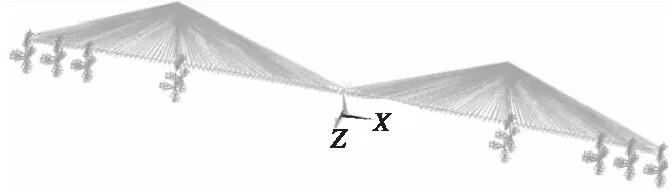
图3 有限元模型图

路面粗糙度函数和粗糙度导数沿主梁纵向(半桥对称)如图4和图5所示。设置车辆系统为2组,每组包含一辆30 t三轴车和一辆20 t双轴车。每组车辆均靠右侧行驶,偏心分别为11.75 m、8.25 m。每组分别从桥梁两端同时同向以100 km/h速度行驶。以0.2 s为时间步长进行有限元分析,提取跨中节点的竖向位移和加速度如图6所示。

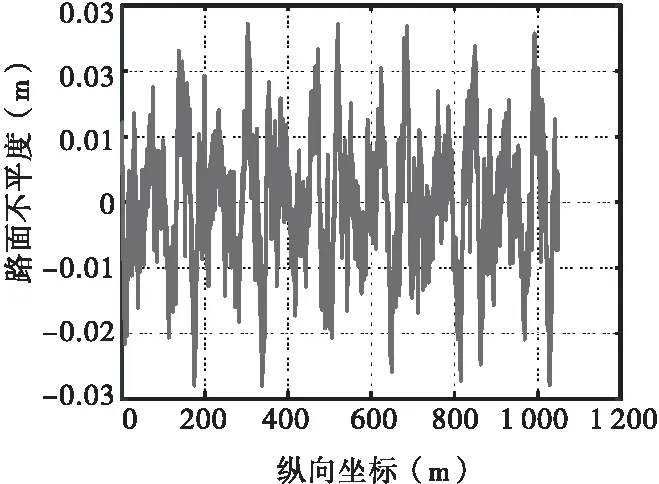
图4 路面不平度示意图

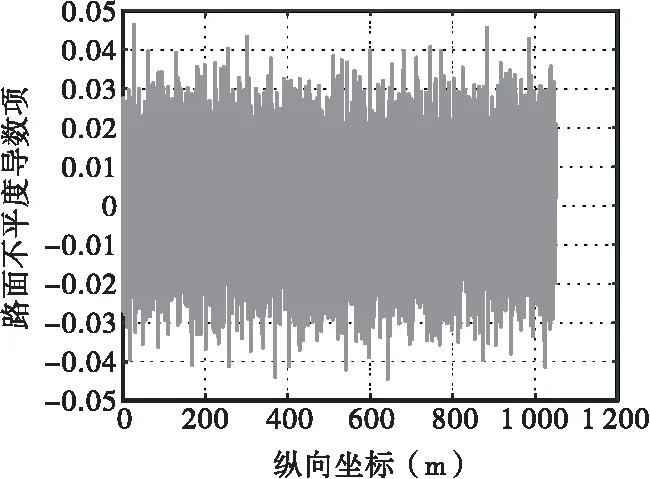
图5 路面不平度导数示意图

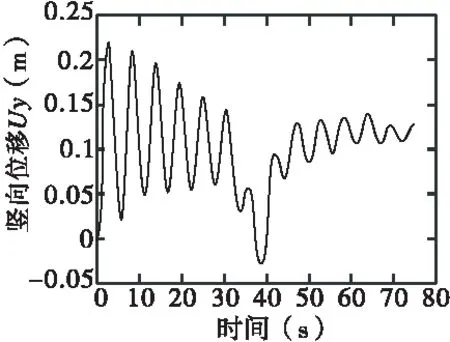
(a)竖向位移

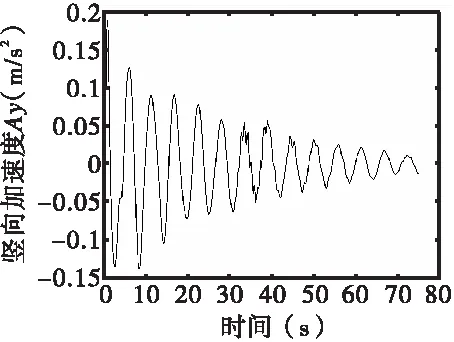
(b)竖向加速度

5.3 结果和讨论

理论分析表明,影响斜拉桥振动的主要因素包括跨径、加劲梁刚度、有无辅助墩等。而影响神经网络训练效果的因素主要包括样本质量、训练次数、神经元数量等。本文选取斜拉桥主跨跨径L、边跨跨径l、辅助跨跨径S、加劲梁竖弯刚度EI和辅助墩个数n共五个参数为输入样本,以斜拉桥的振动响应(包括位移、速度和加速度)为输出样本。主要的计算参数如表1所示。

采用MATLAB神经网络工具箱建立BP神经网络,用BP神经网络对车桥耦合振动下斜拉桥的响应进行拟合,得到三层BP神经网络的权值、阈值。为了便于比较神经网络拟合逼近的效果,仍采用主梁跨中节点的竖向位移、加速度时程进行分析,神经网络结果(ANN)与有限元(FEM)结果对比如图7所示。计算结果表明,基于神经网络的大跨度斜拉桥车桥耦合振动分析结果与有限元计算结果吻合良好。

(a)竖向位移

(b)竖向加速度

6 结语

将斜拉桥结构动力学特点和有限元分析结果相结合作为BP神经网络的输入和输出参数,经过多次训练和验证,实现了大跨度斜拉桥的车桥耦合振动响应的准确预测。主要结论如下:

(1)采用BP神经网络进行大跨度斜拉桥车桥耦合动力响应预测能够满足工程精度要求。

(2)采用BP神经网络进行桥梁结构车桥耦合振动动力响应预测,应通过较多的样本训练并通过试算确定适宜的神经元数量以提高预测精度。

(3)采用BP神经网络进行桥梁结构车桥耦合振动动力响应预测,事先不需要知道任何显式数学表达,而结果可以显式表达,具有较大的灵活性。