The cooling models of Earth’s early mantle
Ting He • Qingwen Zhang • Yun Liu,
Abstract The thermal state of the early Earth’s interior and its way of cooling are crucial for its subsequent evolution.Earth is initially hot as it acquired enormous heat in response to violent processes during its formation,e.g.,the Moon-forming giant impact,the segregation and formation of its metallic core,the tidal interaction with the early Moon,and the decay of radioactive elements,etc.In the meantime,the cooling mechanisms of early Earth’s mantle remain elusive despite their importance,and the previously proposed cooling models of the mantle are controversial.In this paper,we first reviewed several prevalent parameterized thermal evolution models of the early mantle.The models give unrealistic predictions since they were established solely based on a single tectonic regime,such as the stagnant-lid regime,or relied on the disputable existence of the plate tectonics prior to~3.5 Ga.Then we argue that the mantle should have started to cool down from a very hot state after the solidification of the ferocious magma ocean.Instead of using one single scaling law to describe a single-stage model,we suggest that an episodic multi-stage cooling model(EMCM)of the early mantle could be more plausible to account for the mantle’s early cooling process.The model reconciles with the fact that the mantle cools down from a hot state prior to~3.5 Ga and can also explain the well-constrained post-3.5 Ga thermal history of the mantle.
Keywords Thermal evolution ∙Mantle ∙Parameterized model ∙Episodic cooling ∙Early mantle
1 Introduction
The thermal history of terrestrial bodies (i.e.,planets,moons,and asteroids) in the solar system is crucial for its evolution since the thermal state dominates their internal differentiation and dynamics (e.g.,the pace of continent growth or onset of the plate tectonics,etc.).The history of the Earth’s evolution depends primarily on its initial thermal state and heat budgets as it cools.While the initial temperature serves as a starting point of Earth’s secular cooling evolution,the heat budget of Earth,or Earth’s mantle,concerns the difference between the rate of internal heat production and the rate of heat dissipation through its surface to space.To determine the thermal evolution history of Earth’s mantle,which composes~67% mass of the Earth,the rate of heat transport from the core to the mantle,the heat generation in the mantle,and the route and rate of heat loss of the mantle through the lithosphere are key issues of interest,especially for the little-known Hadean-Paleoarchean Earth.
In terms of heat generation,Earth gains enormous heat in response to dramatic geologic processes during its early formation processes (e.g.,accretion,core-mantle differentiation),resulting in a hot initial thermal state.Subsequently,the dominating mechanism of heat production turns to radiogenic heating due to the decay of radioactive elements in the mantle.If estimated based on the radioactive decay law,~4–5 times more heat could be generated in the early Hadean mantle due to the decay of the long-lived radioactive isotopes(e.g.,235U,238U,232Th,and40K) than that of today’s mantle (Turcotte and Schubert 2002).In addition,other potential mechanisms of heat generation include tidal heating caused by the Earth-Moon interaction in the early Hadean(Heller et al.2021)and the release of latent heat during metallic core segregation(Schubert et al.2001) are important.
When it comes to heat loss,cooling of the mantle is mainly controlled by the specific tectonic regime (e.g.,plate tectonics,stagnant lid tectonics,etc.)of the Earth at a certain time,and the rate of heat loss varies significantly for different tectonic regimes.That is because the heat is transferred from the hot interior of a terrestrial body through convection of the mantle and conduction of its lithosphere before releasing it into space via radiation.Therefore,the vigor of mantle convection,the thickness of the lithosphere,and the extent to which the lithosphere participates in mantle convection largely determine the rate of heat loss for a given tectonic regime.
The thermal models of the early Earth remain controversial since several longstanding questions remain.First,the petrological records (Herzberg et al.2010) providing clues of the mantle’s cooling are confined to Earth’s history since~3.5 Ga(Fig.1).The starting point of the mantle’s cooling remains poorly constrained due to the scarcity of the earlier geological records.Second,if taken the temperature soon after the solidification of Earth’s last magma ocean as the starting point of temperature decrease of the mantle’s thermal evolution,it is still not clear how the mantle cools from this much hotter state than today.In addition,what makes the thermal evolution of the mantle particularly complicated is that the cooling of the mantle involves various non-linear interactions between its temperature and its rate of heat loss in response to various early processes.The thermal state of Earth,to a large extent,determines the style of the operating tectonic regimes at that time.The complicated behaviors of a particular type of tectonic regime could in turn influence Earth’s overall cooling rate.

Fig.1 Mantle potential temperature over Earth’s history was revealed by the post-3.5 Ga petrological records [Data source:Herzberg et al.(2010) and Korenaga (2008)] with an extension to an earlier period before 3.5 Ga.The result of the secular cooling model(dashed line)is compared with the petrologically inferred trend of the potential mantle temperatures from non-arc basalts (blue dot).The pre-3.5 Ga cooling history of the mantle is derived from a thermal model based on a simplified heat budget with a constant rate of heat loss (dashed line)
William Thompson (later Lord Kelvin) was the first to propose the model of the thermal evolution of the Earth in 1895,assuming that the Earth cools from a hot state purely by heat conduction(Thomson 1895).The age of Earth was believed to be less than 100 Ma because the estimated time scale of the Earth’s cooling down to the present temperature from an initially molten state is~50–100 Ma(Schubert et al.2001).After the discovery of radioactivity and the introduction of the concept of mantle convection,the roles of heat production due to the decay of radioactive elements and transfer of heat via convection in the mantle cooling are found to be crucial and predominating in its thermal evolution (Becquerel 1896;Curie 1898;Tozer 1965,1972).
Based on these revolutionary approaches,the so-called‘‘parameterized’’ thermal models are proposed to estimate the trend of mantle cooling with time with simplified assumptions of mantle cooling due to its convection.These models try to establish simplified relationships between the vigor of mantle convection and the rate of heat loss through the Earth’s surface (Sharpe and Peltier 1978;Schubert et al.1980).However,these early models yield unrealistically hot states of the early mantle (i.e.,the so-called‘‘thermal catastrophe’’) if one tries to derive the thermal state backward from the present-day temperature of the mantle with a given heat budget.On the contrary,if deriving the cooling history of the mantle from an initially hot state with a given heat budget,one would get an unreasonably overcooled ‘‘frozen state’’ instead (Davies 1980;Christensen 1985).
Subsequently,a great deal of effort was put into improving the models and establishing new relationships between the surface heat flux and the temperature of the mantle (i.e.,the heat flux-temperature scale law).To this end,the high-temperature trend predicted by the parametric models is shifted to a less unreasonable range by artificially changing the key parameters (e.g.,the Urey ratio) (Christensen 1985;Gurnis 1989).On the other hand,some geodynamics processes (especially plate tectonics) were considered to overcome the drawbacks of the classical models based on simpleQ-Tscaling laws (Conrad and Hager 1999,2001;Korenaga 2003;Combes et al.2012).However,whether or not plate tectonics existed during the first billion years of Earth’s history is highly debatable.
This paper aims to review several parameterized models of the thermal evolution of the mantle.After analyzing the inconsistencies between the results and observations,we provide a new model (EMCM) involving episodic,multistaged processes to explain the mantle’s early cooling history.
2 Key issues in the thermal evolution of the mantle
2.1 Petrological records and their issues
A direct approach to investigate the thermal evolution history of Earth’s mantle is to estimate the temperature and the age of mantle-derived rock as it forms via proper geothermometers and dating methods (e.g.,the Re-Os system).Among others,the mantle potential temperature(Tp),an assumed temperature of the mantle material if it rises to the surface adiabatically without melting(McKenzie and Bickle 1988),is often used to reflect the mantle’s thermal state at a certain time.Tpcan be estimated through various geothermometers (Putirka 2005,2009;Herzberg and Asimow 2008).For example,the correlation between MgO content in the primary magma of non-arc basalts and the mantle potential temperature is used to estimateTpover the past~3.5 Ga,during which petrological records are available (Herzberg and Asimow 2008;Herzberg et al.2010).The results reveal that mantle temperature decreases by~200 °C in 3.5 Ga (Fig.1).
Herzberg et al.(2010) extend the mantle’s cooling history revealed by the petrological records to a much earlier period~4.0 Ga by extrapolating the availableTp-age data.The result indicates a relatively cool mantle temperature with a turning point at~3.5 Ga.In other words,the mantle heated up before~3.5 Ga and started to cool since then (Fig.1).However,the extrapolation of the mantle’s cooling trend seems problematic.First,the results derived from the increasingly rare rock samples towards~3.5 Ga are increasingly unreliable,i.e.,with a significant spreading distribution(Fig.1);Second,the rock samples earlier than~3.5 Ga are absent from the geological records.
2.2 The starting and ending points of the mantle’s early thermal evolution
The cooling trend of the mantle from~3.5 Ga to today is loosely constrained by the petrological data (Fig.1) from Herzberg et al.(2010) and Putirka (2016).What remains controversial is the early history of mantle cooling prior to 3.5 Ga.Since the geological records of the mantle’s cooling are incomplete,the mantle’s thermal evolution during the early Earth is hard to trace.
Despite the lack of sufficiently accurate petrological constraints,there are general agreements about Earth’s early thermal state soon after its formation.The early mantle and its precursor,the magma ocean,was born very hot during Earth’s accretion stage and with a temperature much higher than the turning point shown in Fig.1.At that time,Earth experienced violent processes such as the core formation and decay of short-lived radioactive elements(Albarède and Blichert-Toft 2007).Since the mantle was formed after the solidification of Earth’s last magma ocean,the temperature of the sub-solidus state of the silicate (i.e.,the early mantle) is certain (Abe 1997;Katz et al.2003).The thermal state at which Earth’s last magma ocean solidifies corresponds to the thermal state of the newborn mantle,which can serve as the starting point of its thermal evolution and can be bounded by the solidus temperature of the mantle rocks.We argue that the pre-2.0 GaTp-age trend is somewhat misleading and neglects the fact that Earth is born hot,and the subsequent thermal evolution of the mantle should have been an overall cooling process from that point.The well-constrained cooling history starts at~2.0 Ga and can serve as the ending point of the mantle’s early thermal evolution (C in Fig.2b).

Fig.2 (a) The relationship between rates of surface cooling Q,internal heating H (both expressed in terawatt,TW),and mantle potential temperature Tp (red line).The variation of heat production of radioactive elements with time (black line).(b) Paths of mantle’s cooling with forward/backward integrations of the thermal evolution equations in time.The backward approach lead to an unrealistically hot state of‘‘thermal catastrophe’’(red curve),while the forward one yields an unreal ‘frozen state’’ of the mantle (blue curve) (Davies 1980;Christensen 1985).The point C starts at~2.0 Ga and serves as the ending point of the mantle’s early thermal evolution
The mantle’s cooling in an overall decreasing manner from a hot state before~3.5 Ga is distinctive to those predicted by Herzberg and Asimow (2008) and Herzberg et al.(2010),which features a relatively cool starting point of the mantle at~4.0 Ga (Fig.1) and is used to test the results of a highly simplified thermal model,which assumes a highly simplified heat budget with a constant rate of heat loss and internal heating exponentially increases due to decay of long-lived radioactive elements Herzberg et al.(2010).Such predictions cannot compromise the fact that Earth is initially much hotter.It is hence difficult to explain why the mantle has such a relatively low temperature before~3.5 Ga (Fig.1).
3 Existing models of mantle’s thermal evolution
3.1 Parameterized convection models
The major type of thermal model of the mantle is the socalled ‘‘parameterized’’ convection model based on boundary layer theory and a whole mantle convection hypothesis.In the parameterized models,an initial thermal state and an assumption of the global heat budget of the mantle are required.Given an initial thermal state of the mantle,such models evaluate its cooling process based on the law of energy conservation.The models feature utilization of the correlation between the vigor of mantle convection and the rate of heat loss (i.e.,the scaling law between heat flux and the mantle temperature)and consider the heat generation due to the decay of radioactive elements (Schubert et al.1979;Davies 1980;Christensen 1985).Despite the complex nature between mantle convection and surface heat loss,the parameterized models assess the cooling processes using simpleQ-Trelations with few parameters (Sharpe and Peltier 1978).
To specify the mantle’s heat budget,the decay of radioactive elements is considered the primary source of heat generation in the mantle,and mantle convection is assumed to be the primary way of heat transfer before the heat is conducted by the lithosphere and dissipated into space (Davies 1980;Schubert et al.1980,2001;Christensen 1985;Jaupart and Mareschal 2010).Therefore,the thermal evolution of the mantle can be described by
whereTis the average mantle temperature in terms of potential temperature (Tp),His the average rate of heat production of the mantle (W),Qis the mantle’s cooling rate (i.e.,the overall rate of surface heat loss of Earth in terms of W).HandQon the right-hand side of Eq.(1)are crucial for the long-term thermal evolution of the mantle since the imbalance between the heat generation and the surface heat loss dominates the rate of change of mantle temperature.In parameterized modes,time integrations of terms in Eq.(1) yield cooling paths with given initial temperatures.
In most models,the decay of long-lived radioactive elements is considered the primary heat source in the mantle in most of Earth’s history.Accordingly,the coremantle heat transfers and heat generated in continents are usually neglected to simplify the evaluation of heat generation.The decay of short-lived isotopes (e.g.,26Al and60Fe) in the early mantle releases enormous heat due to their high abundances (Lee et al.1977;Gargaud et al.2013),but the heat decreases rapidly because of their short half-life (~0.72 Ma for26Al and~1.5 Ma for60Fe)(Stacey and Davis 2008).Therefore,soon after the formation of the solar system,the short-lived radioactive isotopes were exhausted in a few million years,only the heat generation due to long-lived isotopes238U,235U,232Th,40K (with half-lives up to 0.7–14 Ga,Table 1) are still significant (Turcotte and Schubert 2002).The heat production of the mantle can thus be estimated by weighted average values of the radiogenic heats of these elements(Korenaga 2006;Davies 2011;Jaupart et al.2015):
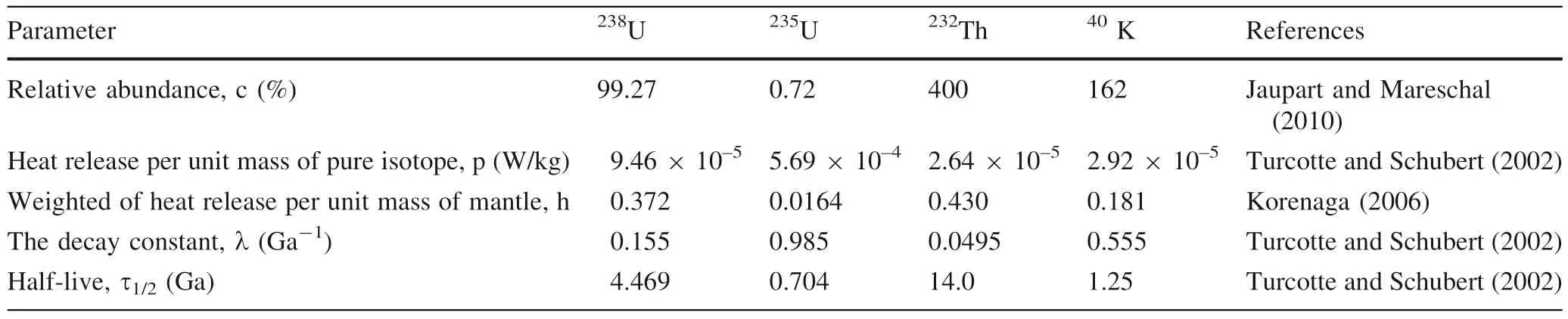
Table 1 Parameters of decay of the long-lived radioactive isotopes in the mantle
where the subscriptidenotes each of the radiogenic isotopes238U,235U,232Th,40K,is the weighted heat release per unit mass of mantle due to decay of isotopei,Ur=H/Q is the Urey ratio(Christensen 1985;Korenaga 2006),Q(0)is the present heat flux of the mantle.The parameters in Eq.(2) are summarized in Table 1.
Another critical step for the parameterized convection models to evaluate the mantle’s thermal evolution is to quantify the surface cooling processes(i.e.,to specify termQ(t)in Eq.(1)).The heat loss of the vigorously convecting mantle is complex due to theQ-Tnonlinearity raised because of the temperature-dependent rheology of mantle rocks.The relationship between mantle potential temperatureTpand surface heat lossQhas been described by simple relations with a few parameters in the parameterized models (Tozer 1972;Turcotte 1980).A thermal model of Earth’s entire history established based on one scaling law is denoted as a classical model herein for simplicity of descriptions.In these models,mantle convection is considered the primary mechanism of heat transfer,and a wellknown scaling law between the vigor of mantle convection and the surface cooling is established as
whereNuis the Nusselt number,Rais the Rayleigh number,andRacis the critical Rayleigh number determining whether convection onset andais a constant(~1)that varies with choose of convection systems (Davies 1980).The power-law exponent β in Eq.(3)determines the sensitivity of the surface heat flux to the mantle convection with a range of 1/3–1/4 (i.e.,1/3 for a basal heating convection and 1/4 for an internal heating convection).Equation (3) is derived based on boundary layer theory,and parametersaand β can be calibrated from convection experiments with constant viscosity(Turcotte and Oxburgh 1972;Schubert et al.1979).TheNu-Rascaling law has been widely used in thermal models with mantle convection (Davies 1980).The Nusselt number in Eq.(3) indicates the heat transfer efficiency of the mantle and is defined as the ratio of convective heat flux to conductive heat flux:
measures the vigor of the mantle convection,andRais inversely proportional to mantle viscosity ν sensitive to temperature.The temperature-dependence of mantle viscosity can be described by the following Arrhenius equation:
Equations (5–6) suggest that a slight temperature variation will cause a dramatic change in mantle viscosity and the vigor of mantle convection.By combining Eqs.(3–6),the surface heat fluxQcan be parameterized as a function of the mantle temperature:
As shown in Eq.(7),Qhad a power-law dependence on mantle temperatureT,and the rate of surface heat loss of the mantleQis thus sensitive toTpifTpis to represent the mantle’s thermal stat.β is also a crucial parameter signifying the influence ofTponQ.ThisQ-Tscaling law is key for the parameterized models to evaluate the rate of mantle cooling over a certain period.Substituting Eqs.(2–8) into Eq.(1),we have a differential equation of the mantle’s thermal evolution in the following form:
wheref1andf2are two parameters controlling relative contributions of the heat generation and the mantle convection to the mantle’s thermal evolution:
Parameters in Eqs.(4–10) are summarized in Table 2.
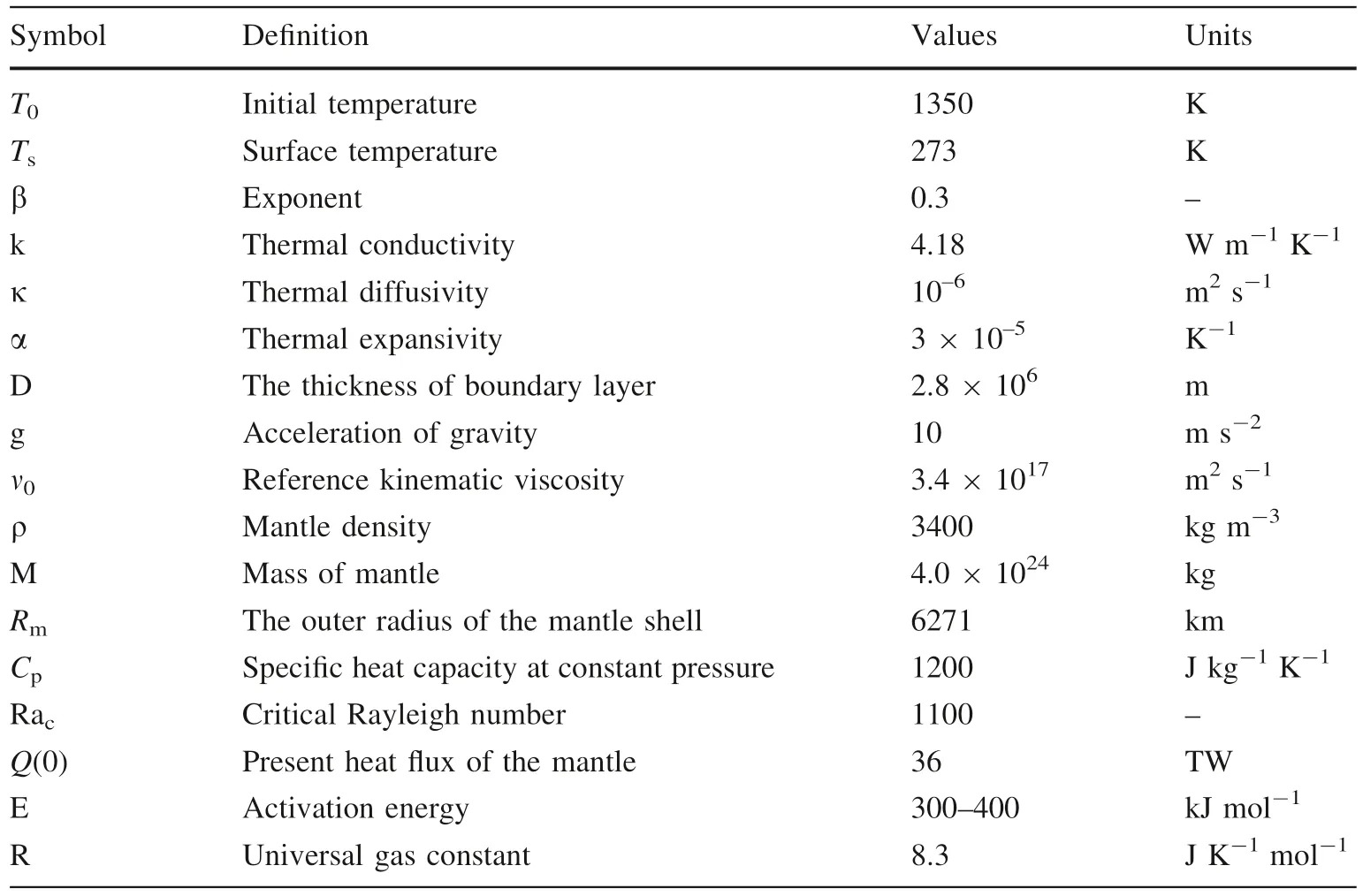
Table 2 Parameters used in the thermal models
3.2 Limitations of the parameterized models
The rate of increase/decrease of mantle temperature depends on the difference betweenQandTfor a given initial thermal state.There are two methods of time integrations of Eq.(8)to estimate the mantle’s thermal history.One approach is to derive the mantle temperature forwards from an initial hot state in Earth’s early history toward the present day (Fig.2b,path B to B*from a starting point B at~4.5 Ga) to infer mantle’s subsequent thermal evolution (Schubert et al.1980;Davies 1993).The alternative way is to calculate cooling history backwards from the current mantle temperature (e.g.,Tp~1350 °C) (Fig.2b,path A to A*) to its earlier history.
Both methods predict a monotonously decreasing cooling history of the mantle if the rate of the mantle’s heat loss is always lower than its rate of heat generation (i.e.,Q<Hover almost the entire cooling history of the mantle).For the forward method,the Earth’s mantle cools too rapidly such that it would reach a ‘‘frozen state’’ (Fig.2b,blue curve) sinceQincreases withT,which suggests the hotter mantle may have experienced a faster cooling stage at its first billion years of history.Similarly,the backward approach causes the mantle to an unrealistically hotter thermal state (far above the liquidus temperature of the mantle rocks~1800 °C) back only to~1.5 Ga with an initial temperature ofTp~1350 °C (Fig.2b,red curve).The deductive thermal state is unreal and is known as a‘‘thermal catastrophe’’ (Schubert et al.1979;Christensen 1985).Neither the ‘‘thermal catastrophe’’ (unrealistically hot) nor the overcooled (unrealistically cold) trend predicted by the classical parameterized models can match the available petrological records (Fig.2b,blue dots),which suggest a moderate decrease in the mantle temperature only by~200–250 K since~3.5 Ga.These mismatches are sourced from the parameterized models using simple scaling laws of theQ-Trelation(Fig.2a,red line)featuringQincreasing withT,i.e.,a higher mantle temperature would facilitate convection of mantle and thus more rapid heat loss (Schubert et al.1979;Sharpe and Peltier 1979;Davies 1980;Christensen 1985).
To adjust the classical model and obtain more ‘‘reasonable’’ predictions consistent with the cooling trend‘revealed’’by the petrological records,e.g.,Herzberg et al.(2010),another approach is to adjust the Urey ratio and scaling law’s parameters (e.g.,β) artificially to avoid the‘thermal catastrophe’’ or the overcooled trend of mantle’s cooling.
The first way to correct the results of the classical model and avoid the unreal cooling history is to disregard the observed heat budget and artificially change the Urey ratio,which can significantly affect the mantle’s cooling.The present-day Urey ratio of~0.21–0.49 of the mantle cooling system is estimated based on the current level of heat generation in the mantle (due to decay of U,Th,K)and the average heat flux at Earth’s surface (McDonough and Sun 1995;Jaupart et al.2015).Increasing the Urey ratio to a much higher level of over 0.7 can yield a cooling path that significantly postpones the occurrence of the‘thermal catastrophe’’ (Fig.3),which cannot be avoided(Fig.4).

Fig.3 The trend of thermal evolution with different Urey ratios.Modified from Korenaga (2006,2013)

Fig.4 Cooling of mantle temperature over time for β=0.1 and different values of Urey ratios and β=0.3 with the Urey ratios Ur(0)=0.84 [Modified from Christensen (1985)]
Other approaches try to modify the parameter β in Eq.(3)since β determines the degree of dependency of the heat loss (Nu)on the vigor of mantle convection (Ra),and thus the dependency of the rate of cooling (Q) and mantle temperature (T).The classical parameterized models are established based on boundary layer theory and mantle convection systems with constant viscosity.The model yields a power-lawNu-Rascaling law in the form of Eq.(3) with an exponent β~0.3 obtained by experiments.However,the strong temperature dependency of the mantle’s viscosity is ignored in thisNu-Rascaling law and is considered in a subsequent model (Christensen 1984).The results of Christensen’s model indicate that the mantle flux is dominated mainly by the viscosity of the boundary layer (lithosphere) and a low value of parameter β <0.1 in Eq.(7)for a boundary layer with high viscosity contrast.The decreasing of β indicates a weakerNu-Radependency,thus decreasing the dependency of heat flux on mantle temperature.This further suggests a decoupling between heat loss and temperature despite the temperature dependency of the viscosity of the mantle.The model with a small value of β predicts a constant heat flow of the mantle regardless of the mantle’s thermal state.
In Christensen’s model,the mantle’s cooling via convection is confined to a ‘‘stagnant-lid’’ regime,which assumes that convection occurs under one single rigid lithosphere of Earth,although the mantle’s viscosity decreases at a high temperature.Other authors argue that,in this case,plate tectonics would have occurred and serves as the dominating mechanism of the mantle’s heat loss(Gurnis 1989;Conrad and Hager 1999).If so,a newNu–Rarelationship with β~0.3,similar to the case in the classical models,is established when weak zones are added to the rigid plate in the models similar to Christensen’s model(Gurnis 1989).
3.3 The incorporation of plate tectonics
The second category of approaches discussed above tries to modify theQ-Tcorrelations by taking the possible dynamic process on early Earth (e.g.,the plate tectonics) into consideration (Sleep 2000;Korenaga 2006;Moore and Lenardic 2015).The modification of theQ–Tscaling law aims at decreasing the cooling rate as the mantle is hot to avoid the unrealistic cooling trends discussed above.Since the value of β controls the sensitivity between the mantle temperature and the surface heat flux,the decrease of β leads to a decoupling between surface heat flux and mantle temperature(Christensen 1985).Similarly,the introduction of plate tectonics could reduce the sensitivity of the mantle’s cooling rate on its thermal state by considering the resistance of plate bending at the subduction zone in the parameterized model(Conrad and Hager 1999).Therefore,in a plate tectonics context,as the subduction of an oceanic plate requires its bending and has to overcome its rigidification,mantle cooling is closely related to the strength of the oceanic plate as it subducts.Assuming that the plate thickness remains constant over a wide range of mantle temperatures,the model yields a scaling law with exponential value β=0 (Conrad and Hager 1999).Korenaga(2003) argues that the thickness of the boundary layer(lithosphere) is one of the key parameters controlling the dynamical processes as well as temperature.The assumption of constant plate thickness over time proposed by Conrad and Hager (1999) is unlikely because the plate thickness is limited by its convective instability.Korenaga(2003) instead introduced a model with the temperature dependence of viscosity and plate thickness and defined plate thickness by considering the dehydration by melting at mid-ocean ridges and accordingly re-derived the scaling law based on plate tectonic convection (Korenaga and Jordan 2002;Korenaga 2003).He calculated the plate thickness as a function of mantle temperature variation.The resultant scaling law shows a negative sensitivity β=-0.15 to mantle temperature as the plate thickness varies (Korenaga 2003).
4 The episodic multi-stage cooling model(EMCM)
To explain the thermal history revealed by the petrological observations at least since~3.5 Ga and avoid unrealistic predictions of the mantle’s cooling history,we argue that the mantle should have cooled from a hot state in an episodic,multi-stage manner.For simplicity of descriptions,a thermal model of Earth’s entire history established based on one single scaling law is denoted as a single-stage model herein in this paper.Alternatively,a model considering multiple mechanisms of heat loss at different stages of mantle’s cooling and transitions between them is called the multi-stage model.We further suggest an episodic multi-stage cooling model(EMCM)for the cooling history of the mantle of the early earth.
4.1 The feasibility of early plate tectonics
Earth’s tectonic evolution is closely linked to its thermal evolution since the tectonic movements on a lithosphere scale and is driven by the generation and transfer of heat in the Earth’s interior and heat loss from its surface through mantle convection.Because the single-stage model based onNu-Rascaling law fails to predict the thermal evolution of the mantle,plate tectonics are introduced to fixed scaling law with β <0 as discussed in Sect.3.A critical question left to consider is whether plate tectonics exists in the pre-3.5 Ga Earth or not.Therefore,the correction of the classical thermal models shifts our attention to the possibility of early plate tectonics.Although plate tectonics dominates the heat loss of the present-day Earth,it is debatable whether this tectonic regime is feasible over the early history of Earth (van Hunen and Moyen 2012;Moyen and van Hunen 2012).
While it is difficult to figure out whether the plate tectonics can operate during the Hadean-Eoarchean because of the absence of geological records,numerical modeling investigating the feasibility of subduction on the early Earth with an assumed hot mantle has been carried out(Kröner 1981;Cawood et al.2006;Davies 2006;O’Neill et al.2007,2017;Sizova et al.2010;Gerya 2011,2014;Foley et al.2014;Ernst 2017).The results show that it is difficult for large-scale subduction,which is how a rigid lithosphere anticipates mantle convection and enhances its cooling in a framework of modern plate tectonics,to occur and sustain on the early Earth.The subduction may be intermittent if the upper mantle is hotter than today (van Hunen and van den Berg 2008).First,the mantle might be much hotter,as discussed in Sect.2,and the oceanic plates generated in a hotter mantle might be too buoyant to subduct since the oceanic crusts would be significantly thicker than their modern counterparts.This is because oceanic crusts are generated through the partial melting of the asthenosphere under the mid-ocean ridge,and the degree of melting of a hotter mantle would be much higher than it is today (van Thienen et al.2004;Johnson et al.2014).Second,the slabs (the subducted parts of the oceanic plates),if there are any,might be weak and easier to break off if the ambient mantle is hotter because the strength(partly embodied as their viscosity) of an oceanic plate is strongly dependent on their thermal state.The assertion of the existence of plate tectonics in early Earth requires careful assessments and reliable evidence.
4.2 Episodic scenario of mantle’s early cooling
4.2.1 Limitations of the single-stage models
Bearing in mind that the mantle should have cooled from a hot state since the solidification of the magma ocean instead of being cold initially and warming up afterward,e.g.,Herzberg et al.(2010)and Korenaga(2013).The path of the mantle’s cooling remains important and cannot be well constrained by the parameterized models discussed in Sect.3.In these models,the cooling of the early mantle has been described by a singleQ-Tscaling law established based on one single type of tectonic regime (e.g.,the stagnant-lid regime in the classical parameterized models).
The models are problematic because (i) it is unreasonable to assume only one type of single regime and scenario of cooling exists on the early Earth.(ii) most of the early processes can result in monotonously decreasingQ–Tscaling law (e.g.,theQ–Trelationship based on theNu-Rascaling law or the radiation-dominatingQ∝T4scaling law) if the early heat budget of the mantle is unbalanced(i.e.,Qis always lower thanHover time).Inevitably,any scaling law considering merely one single scenario of the tectonic regime would yield an unrealistic prediction of thermal evolution(e.g.,either the‘‘thermal catastrophe’’or the overcooled state shown in Fig.2b),in which the cooling curve is steep as the temperature is high and becomes flat as temperature decreases (Fig.3),as long as theQ–Tscaling is expressed as a function ofQincreases withT.(iii)The models have struggled to fit the ambiguous trend of the extended path around the~3.5 Ga period of mantle’s cooling,which indicate a relatively cool starting point of mantle’s cooling before~3.5 Ga(Herzberg et al.2010)(Fig.5).This contradict to the fact that the mantle is hot as the Earth’s magma ocean solidifies.It is hard to explain why the mantle is initially cool and warms up before its cooling since~3.5 Ga.

Fig.5 The plate tectonics thermal evolution trend with different Urey ratios.Modified from Korenaga (2006)
4.2.2 Episodic cooling of the mantle due to transitions of tectonic regimes
As discussed above,there is a need to reassess the cooling paths of the early mantle due to the misleading of unreliable early petrological records.Now that a singleQ-Tscaling law fails to explain the cooling path of Earth’s mantle,and the starting point and end point of the mantle’s early cooling history (i.e.,the points A and C in Fig.2b,respectively) are certain,a thermal model considering multiple scaling laws is inevitably required to explain the enigmatic pre-3.5 Ga stage of mantle cooling.In other words,to ‘‘connect’’ points A and C,an episodic scenario of the early mantle’s cooling is an intrinsic consequence if we abandon the single-stage models.
The multi-stage models should fulfill the following conditions: (i) the models should include different scaling laws,which are established based on different tectonic regimes possible for early Earth (not confined to the stagnant-lid regime in classical models),such as magma ocean regime and the plate tectonics (Sleep 2000).(ii) The models should allow switches ofQ–Tscaling laws to reflect the transformations of regimes favorable at different stages in Earth’s early history (Fig.6).

Fig.6 Cartoon illustrating transitions of cooling scaling laws modified from Sleep (2000) (a),the resultant heat budget with time(b),and the resulting episodic cooling (c)
Since different tectonic regimes are taken into consideration to describe the early cooling of the mantle in multistage models,the corresponding mechanisms of surface heat loss andQ–Tscaling laws are involved,which can be distinct from each other.The episodic reversal of the heat budget thus causes the cooling path to be episodic(Fig.6).The episodic reversal further requires frequent transitions of different types of tectonic regimes throughout Earth’s history.
Sleep (2000) outlines the possible scenarios of transitions among different cooling regimes for terrestrial planets,including Earth.Once the thermal state reaches the point (e.g.,point B in Fig.6a),the tectonic regime dominating the heat loss of a terrestrial planet is transformed to others abruptly (point C in Fig.6a).Accordingly,the heat budget could reverse in response to this abrupt transition,from a state ofQ>Halong curve AB to another along curve CD.The reverses of heat budget in this way lead to an oscillating style of the evolution ofQrelative to the rate of internal heatingHwith time (Fig.6b),which further yields a cooling history in an episodic manner (Fig.6c).
Taking the Earth as an example,it is widely believed that its mantle may have undergone distinct stages of cooling over its entire geological history,during which transitions of theQ-Tscaling laws and changes in its heat balance may occur several times.A hot magma ocean is supposed to have formed at the end of Earth’s accretion stage,which cools rapidly as the rate of heat loss via surface radiation as cooling rate (following aQ∝T4scaling law)significantly exceeds the rate of radiogenic heat in the mantle (process A-B in Fig.6a).As the magma ocean freezes,the cooling mechanism of the newborn mantle possibly switches to tectonic regimes (e.g.,the plate tectonics) with thermal conduction and convection (point C).If the Hadean rate of heat generation remains higher than that of the plate tectonics,which meansQ>H,the mantle will heat up again (process C–D in Fig.6a).These cause the evolution of mantle temperature in a back-and-forth manner over time,as long as the rate of heat generation is lower than the cooling due to radiation and higher than plate tectonics—the reversal of relative values heat budget.
5 Discussion
5.1 Constraining Earth’s thermal history by the petrological records
The petrologically constrained trend of the mantle’s thermal evolution should not be considered a definitive benchmark for thermal models,as there are several issues with its interpretation.Firstly,the limited number of thermometry data points from rock samples at 3.5 Ga,and the absence of further actual data points to support the claim that the temperature at that time was low,call into question the reliability of this trend.In addition,the presence of various factors leads to errors in the temperature measurement data points,resulting in unreliable results that may not accurately represent the temperature variation of the mantle(Herzberg and Asimow 2008,2015).Moreover,the lack of data points before 3.5 Ga makes it challenging to determine the exact starting point of mantle temperature evolution.To avoid being misled by the petrological record from Herzberg et al.(2010),additional thermometry data from early Earth samples are urgently needed to constrain the mantle’s cooling history better.
5.2 Mechanisms for mantle’s episodic thermal evolution
Since an episodic,multi-staged manner of the cooling of the mantle’s early history is required to explain the fact that the mantle should have cooled from a hot state and that the cooling rate for a hot mantle is likely to be higher,the actual processes or mechanisms possible on the early Earth are required to account for this manner.Several mechanisms of the transitions between distinct regimes.
The first possible transition of the cooling mechanism of the Earth occurs at the end of its magma ocean stage,when the Earth’s last magma ocean cools rapidly via thermal radiation at its surface and gives born to the hot mantle,and the end of the magma ocean regime is followed by cooling of the newborn,sub-solidus mantle via its convection.Second,the demise of a stagnant-lid regime due to a significant decrease in the mantle’s viscosity as it cools could be a plausible way of transitioning to other cooling regimes(Sleep 2000;Karato and Barbot 2018).Similarly,the demise of a plate tectonic regime due to trench lock or ridge lock as an oceanic crust thickens as the mantle gets hot or the mid-ocean ridge ceases to melt as the mantle cools (Fig.6a).As discussed in Sect.4.1,numerical modeling of the early plate tectonics when the mantle is significantly hotter than today clearly shows episodic subduction of slabs due to their frequent break-off in a hot ambient mantle,which leads to intermittent subduction of the oceanic plates,like long-term episodic (O’Neill et al.2007;Davies 2008) and short-term episodic behavior (van Hunen and van den Berg 2008;Moyen and van Hunen 2012).In addition to the periodicity due to the temperaturedependent rheology of the slab,a variant of the vigor of mantle convection in response to phase changes and layering of the mantle could also lead to fluctuation of the cooling rate of the mantle.Davies(2008)presents a model of mantle cooling considering the subduction of the oceanic crust with buoyancy in a depth range of 660–750 km.Because the basaltic crust is buoyant at 0–660 km,the transition from basalt to a denser phase occurs deep in the lower mantle,the subduction of the oceanic crust (of basaltic composition) tends to accumulate at the transition zone and serves as a ‘‘basalt barrier’’,which could block the vertical flow of the mantle and causes layering of the mantle convection (Davies 2011).As mantle convection stops to layer(for a period of~100–150 Ma),the mantle materials overturn and lead to their exchange between the upper and lower mantle due to the breakup of layers,episodically delaying the cooling of the mantle.The episodic overturns become more frequent and less violent as radioactive heat decreases(Fig.7).Davies’models require that plate tectonics have operated throughout Earth’s entire history (Davies 2007).So far,all the possible transition mechanisms of the mantle’s cooling remain uncertain.

Fig.7 Episodic evolution of mantle potential temperature in response to mantle layering.Modified after Davies (2008)
5.3 Insights of cooling mechanism from other terrestrial bodies
Our poor understanding of Earth’s early secular cooling leads to the utilization of the oversimplified cooling models of the mantle.Despite our limited knowledge of Earth’s early secular cooling due to a lack of geological records,abundant extraterrestrial observations from other terrestrial bodies in the solar system can provide insights into Earth’s early tectonic evolution and its thermal history.Among others,magmatism extensively observed on terrestrial bodies may play a crucial role in determining their cooling history.
The intense volcanic activities observed on Jupiter’s moon Io indicate that volcanism can dominate the heat loss on a terrestrial body in the solar system.About 100 TW of heat,equivalent to a surface heat flux of~2.5 W/m2(Veeder et al.1994),can be released to space through a rapid eruption of voluminous mantle-derived melts at an effusion rate of~600 km3/a,which is one order of magnitude higher than the present Earth (Zhang et al.2022).These observations lead to the introduction of a volcanism-dominating tectonic regime known as heat-pipe tectonics in the planetary science community(O’Reilly and Davies 1981;Moore and Webb 2013).The heat-pipe tectonics serves as another end-member regime in addition to the plate tectonics and stagnant-lid tectonics for the terrestrial bodies in the solar system (Fig.8).

Fig.8 (a) End-member mechanisms of heat transfer and surface cooling of terrestrial bodies in the solar system.The cooling of magma ocean is dominated by radiation at its hot surface of the early Earth,while the stagnant-lid regime is controlled by pure conduction,and the intermediate advection/convection serves as another endmember mechanism for the mobile-lid and the plutonic squishy-lid regime.(b) Four major tectonic regimes in the solar system.The stagnant-lid regime is pervasive for present-day terrestrial bodies like Moon,Mercury,and Mars,while plate tectonics is unique to Earth.The magma ocean tectonics confines to the earliest stage of most terrestrial bodies and the volcanism-dominated heat-pipe regime are well evidenced on present Io
Similarly,Mercury is believed to have experienced a heat-pipe stage similar to the present-day Io(Peterson et al.2021),and this hypothesis is consistent with observations of MESSENGER spacecraft,including: (i) Mercury’s surface is extensively covered by basaltic lava.It is inferred that large-scale effusive volcanism occurred at~4.0–3.5 Ga ago on Mercury,indicating a magmatically active stage in its early history similar to today’s Io.(ii) Widespread distribution of wrinkle ridges suggests that Mercury’s surface was under contraction as volcanism was active(Solomon et al.2018).The contraction can result from the radial mass circulation (i.e.,melt generation-ascent-eruption-recycle in an Io-like scenario) unique to the heat-pipe regime.(iii) A magnetic field possibly generated~4.0–3.5 Ga ago is detected at Mercury’s surface rocks.A remnant magnetic field indicates the possible operation of a thermally driven dynamo at the time.The latter requires that heat in the interior of Mercury’s core was efficiently transferred to its surface to sustain vigorous core convection.An Io-like heat-pipe regime,which features efficient heat transfer through phase changes and rapid transport of the mantle-derived melts,would therefore promote the generation of this magnetic field.
Mars is also characterized by the existence of large-scale volcanism (Carr 1974;Greeley and Spudis 1981).e.g.,the massive shield volcanos in the Tharsis Rise region active during~4.6–3.8 Ga (Werner 2009).It can be estimated that the volume of melts of~108km3erupted during 200 Ma in this region yields a rate of melt generation of~5 km3/a in the Tharsis Rise (Wilson et al.2009),given that the average thickness of~10 km covering an area of~9.0 × 106km2(Peters et al.2021).Therefore,the effect of volcanic activities on this scale on Mars’cooling should be significant and should be taken into consideration when investigating the heat budget of Mars when the volcanism was active (van Thienen et al.2005;Ruiz 2014).
The discovery of a young surface covered by lavas also suggests that there has been active volcanism on Venus until recently (Ivanov and Head 2013),and it is widely accepted that Venus is a planet active under a stagnant-lid regime (Solomon et al.1992;Phillips and Hansen 1994;Hansen 2018).The role of large-scale magmatism in the cooling of a terrestrial body like Venus cannot be neglected when investigating its heat budget and thermal evolution.
Collectively,the volcanism-dominating heat-pipe regime on Io and the stagnant-lid regime with magmatism on Mercury,Venus,and Mars indicate that magmatism is common in terrestrial bodies’ histories.Their resultant effects of magmatism on surface cooling can be significant and should be taken into consideration in addition to the convection-dominationQ–T(i.e.,Nu–Ra) scaling law,which is based on boundary layer theory in traditional parameterized models discussed in Sect.3.A newQ–Tscaling law with magmatism taken into consideration is therefore needed to improve the parameterized thermal models.
6 Conclusion
In this paper,we reviewed the parameterized thermal models of Earth’s mantle,which give incorrect predictions of the mantle’s early history of thermal evolution.The unrealistic cooling histories are ascribed to the application of improperQ–Tscaling laws and the assumption of the mantle’s early thermal state.Despite new approaches trying to improve the predictions by artificially changing the key parameter in the scaling laws or by introducing new cooling mechanisms involving plate tectonics,we point out that any parameterized thermal model with one singleQ–Tscaling law is not capable of reproducing the mantle’s early cooling history.As an amendment to these models,we argue that the mantle should have cooled from a hot state and undergone multiple cooling stages under instinct regimes with differentQ–Tscaling laws.This results in a cooling history of the early mantle in an episodic manner and is more consistent with the geological records and the physical common sense.
AcknowledgementsThis work is supported by the strategic priority research program(B)of CAS(XDB41000000),Chinese NSF projects(42130114),and the pre-research Project on Civil Aerospace Technologies No.D020202 funded by the Chinese National Space Administration.
Declarations
Conflict of interestOn behalf of all authors,the corresponding authors state that there is no conflict of interest.Yun Liu is Depyty Editor-in-Chief of Acta Geochimica.He was not involved in the journal’s review of,or decisions related to,this manuscript.The authors have no other competing interests to disclose.
- Acta Geochimica的其它文章
- Carbon dioxide partial pressure and its diffusion flux in karst surface aquatic ecosystems: a review
- High-precision double-spike Cd isotopic measurements of seawater by MC-ICP-MS and its application to seawater affected by hydrothermal vent fluids
- Geochronology and geological significance of the strata of the Neoproterozoic Nanhua System,SW North China Craton
- Re–Os and Pb isotope features of pyrite in the Shihangli graphite deposit: implications of coal-generated graphite mineralization in central Hunan,South China
- Magma source and tectonic setting of the Dunde granite in the Western Tianshan: constraints from geochronology,geochemistry,and Sr–Nd–Hf isotopes
- In situ infiltration-precipitation processes in some rock systems

