利用均方误差相对变化规律确定正则化参数及其在PolInSAR测量反演中的应用

林东方,姚宜斌,郑敦勇,廖孟光,谢 建

1. 武汉大学测绘学院,湖北 武汉 430079; 2. 湖南科技大学测绘遥感信息工程湖南省重点实验室,湖南 湘潭 411201; 3. 湖南科技大学地理空间信息技术国家地方联合工程实验室,湖南 湘潭 411201

在大地测量参数反演中,受观测信息不足或模型过度参数化的影响,常会出现模型参数反演病态问题,该问题导致模型参数反演稳定性较差,模型参数估计对观测数据误差极度敏感,严重限制了未知模型参数的估值精度[1-3]。大地测量参数反演中的GNSS空间测量、InSAR(interferometric synthetic aperture radar)地表形变测量、地球重力场测量等领域受病态问题的影响最为广泛[4-10],如何解决病态问题,提高大地测量参数反演质量,是现代大地测量数据处理的重要研究内容[1,11]。

随着卫星与传感器技术的发展,大地测量常通过间接观测反演地球物理参数,并利用物理模型构建观测量与未知物理模型参数之间的函数关系。通过非直接观测信息反演模型参数,受观测条件限制,参数反演病态问题常常难以避免[2,12]。病态问题处理的关键在于减弱或者消除病态性对模型参数估计的不良影响。文献[13]提出的正则化方法,是目前大地测量中应用最为广泛的病态问题解算方法之一。该方法是一种有偏估计方法,其核心是在最小二乘无偏估计的基础上附加稳定泛函约束条件,并通过正则化参数调节稳定泛函的约束作用。因此,稳定泛函与正则化参数的确定是影响正则化方法解算效果的关键。稳定泛函的选择目前主要包括两个方面:一是依据模型参数的先验信息构建稳定泛函[14-15],该方式可利用先验信息补充部分物理参数观测信息,从而缓解观测信息不足引起的模型病态性,具有较好的可行性和实用性[16];另一方面在无法获取先验信息时,稳定泛函常选择为模型参数的二范约束[17-18],即模型参数估值的二次修正,该方式无须获取先验信息,普适性较好,但解算效果过分依赖于正则化参数的合理性与有效性,须确定合理可靠的正则化参数以防止模型参数估值欠正则化或过度正则化。针对正则化参数确定问题,研究人员从不同角度提出了不同正则化参数确定方法。文献[19]从统计学的角度给出了正则化参数的GCV(generalized cross-validation)确定方法,该方法以观测残差平方和最小为准则,通过广义交叉验证方式来确定正则化参数。在此基础上,文献[20]和文献[21]分别在计算方式与计算效率上对常规GCV法进行了改进。然而,受模型病态性影响,模型参数的取值空间较大,以观测值残差平方和最小确定正则化参数难以保证能够得到最优的模型参数估值。文献[22]以平衡正则化估值的平滑度与拟合度为依据,提出了正则化参数的L曲线确定方法,通过该方法确定的正则化参数表现出了较好的稳定性,但利用L曲线拐点确定的正则化参数理论依据不够充分,常出现过度平滑问题[3,12]。文献[23]从有偏估计角度,提出了以参数估值均方误差最小为准则确定正则化参数的方法[24]。文献[25]则分析了有偏估计相较于无偏估计在病态问题解算中的可行性,验证了正则化方法通过正则化参数调节可在均方误差(mean square error,MSE)上优于最小二乘无偏估计方法。均方误差反映了模型参数估值与真值的离散程度,相比于GCV法与L曲线法,最小MSE法使参数估值逼近于真值,有助于提升模型参数的估值精度及可靠性,具有更为充分的理论依据。然而,均方误差的准确计算需要未知模型参数的真值,参数真值在实际应用中无法获得,常以初步估值代替真值迭代计算均方误差[26-27],这导致均方误差的计算对模型参数初值准确性要求较高,难以得到准确的均方误差值,限制了均方误差意义下确定正则化参数的有效性和可靠性。

无法获得先验信息时,模型参数的二范约束函数是目前应用最为广泛也是最为通用的稳定泛函,其正则化矩阵表达为单位矩阵形式,在此情况下,正则化参数的选择决定了模型参数的估计精度。常用正则化参数确定方法可从不同角度给出有效的正则化参数,但仍难以得到理论最优的正则化参数,一定程度限制了正则化方法的病态问题处理效果[28-29]。尽管均方误差最小法在均方误差准确计算上存在问题,但以参数估值均方误差最小为准则确定正则化参数更直观高效,可保障参数估值更接近于真值。鉴于此,本文研究基于均方误差最小准则的正则化参数确定方法。针对模型参数真值未知,均方误差难以准确计算问题,通过分析不同正则化参数下的方差相对变化与偏差相对变化规律,研究利用两正则化参数下的方差与偏差相对变化消除模型参数真值未知影响,综合方差与偏差相对变化分析均方误差相对变化趋势,确定均方误差最大降幅下的正则化参数,进而提升均方误差意义下正则化参数确定的可靠性与稳定性。最后,通过试验验证本文方法的可行性与有效性。

1 正则化方法

病态问题导致模型参数估计对观测数据误差过度敏感,常规解算方法已难以准确获得参数的有效估值。为了改善病态模型参数估计精度,文献[13]提出了一种解算病态模型的正则化算法,是目前应用最为广泛的病态问题解算方法之一。该方法以最小二乘估计为基础,通过引入正则化参数与稳定泛函来改善模型参数估计精度与稳定性[2]。在无法获得先验信息时,稳定泛函常表示为未知参数的二范约束,此时正则化估计准则可表示为

Φ=VTPV+αXTX=min

(1)

式中,V为观测残差向量,V=AX-L;A为观测方程设计矩阵;X为未知模型参数向量;L为观测值向量;P为权重矩阵;α表示正则化参数;XTX为稳定泛函。该情况下,正则化矩阵设定为单位矩阵。由此可得,正则化方法的模型参数估值为

(2)

在采用单位矩阵为正则化矩阵时,正则化参数则成为影响正则化方法解算效果的关键因素。目前应用较为广泛的L曲线法、GCV法及最小MSE法等正则化参数确定方法可有效获得合理可行的正则化参数,但均难以给出稳定优良的正则化参数。因此,最优正则化参数确定方法仍需进一步研究。

2 考虑均方误差相对变化的正则化参数确定方法

2.1 正则化参数变化对均方误差的影响

正则化方法是一种有偏估计方法。相比于无偏估计,正则化法的参数估值是有偏的,其均方误差包含方差与偏差两个部分。由此正则化法模型参数估值均方误差可变换为[23,25]

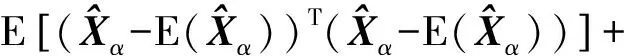
(3)

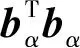
(4)

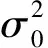
A=USGT

(5)

(6)

式中,U为左奇异向量矩阵;S为奇异值矩阵;G为右奇异向量矩阵;γ为系数矩阵奇异值,γ1>γ2>…>γn>0。对Cα求迹,可得模型参数正则化估值方差为

(7)

由式(7)可得,正则化法可有效实现模型参数估值方差的下降,方差下降程度与正则化参数的数值大小有关,正则化参数越大,方差下降程度越大,反之,则下降程度越小。

由式(2)与式(3)可计算正则化估值偏差为

(8)

(9)

式中,gi为对应于奇异值γi的右奇异向量。由式(9)可知,正则化法所引入的偏差同样与正则化参数大小有关,但与估值方差的变化相反。正则化参数越大,引起的偏差就越大,反之,则引起的偏差越小。

综上,正则化法通过引入偏差降低方差实现均方误差的下降,在正则化矩阵确定的情况下,正则化参数的大小决定了均方误差的下降程度。因此,在均方误差意义下,存在一个最优的正则化参数,使方差下降量减去偏差增加量达到正极值,即均方误差达到最小。通过式(3)、式(7)及式(9)可实现不同正则化参数下的均方误差的计算,进而可确定均方误差达到最小时的正则化参数。但是,由式(9)可以看出,均方误差中偏差的计算需要利用模型参数真值,在实际情形中,参数真值是无法获得的,常规算法以参数估值代替真值实现偏差的计算,但受模型病态性影响,模型参数估值方差较大,准确性较低,以不准确参数估值代替真值计算偏差,常引起均方误差计算有误,难以给出实际最小均方误差下的正则化参数。

2.2 利用均方误差相对变化规律确定正则化参数

利用均方误差最小准则确定正则化参数的关键在于确定模型参数估值的均方误差。在实际应用中,受到参数真值未知的影响,难以通过直接计算得到均方误差的可靠值,进而无法通过直接对比均方误差得到最小均方误差下的正则化参数。

尽管受正则化参数影响下的正则化估值均方误差难以直接计算,但正则化参数对均方误差的影响存在明确的规律性。由式(3)可知,正则化法模型参数估值均方误差的确定可分解为方差确定和偏差确定两个部分。由式(7)和式(9)可知,随着正则化参数的增大,方差呈现负增长规律,而偏差呈现正增长规律,即不同正则化参数下的方差下降量和偏差增加量各不相同。由均方误差统计定义可知,均方误差主要反映了参数估值相对于参数真值的离散程度,而均方根误差则反映了参数估值与真值之间的差异。因此,在参数真值为固定值的情况下,不同正则化参数下的方差下降量变化与偏差增长量变化必然反映在模型参数估值的变化上。鉴于此,本文考虑利用不同正则化参数下的模型参数估值变化及方差下降量与偏差增长量变化实现均方误差的相对变化比较,进而确定出最优正则化参数。

2.2.1 两正则化参数下的方差相对变化量确定方法

无偏估计的均方误差仅包含方差,主要反映了参数估值相对于真值的离散程度。由式(7)可知,方差的准确计算需要利用单位权方差,单位权方差则体现了观测数据的观测精度情况,在所用设备观测精度已明确的情况下,可由设备标定精度计算得到。在设备观测精度未知时,则可通过多余观测信息,采用方差无偏估计方法计算得到。

由最小二乘无偏估计可得包含多余观测的观测值残差向量为[30-31]

V=A(ATPA)-1ATPL-L

(10)

对设计矩阵A进行奇异值分解化简得

(11)

式中,Um由对应于设计矩阵奇异值的m阶左奇异向量组成。单位权方差估计公式可表示为

(12)

由式(12)可知,单位权方差的计算与多余观测信息有关,与奇异值的大小无直接关联,因此,在可获得多余观测的情况下,能够实现单位权方差的估算,利用估算的单位权方差结合式(7)即可得到不同正则化参数下的方差。设两个相邻的正则化参数值分别为αj-1和αj,其对应的正则化估值方差分别为

(13)

(14)

无偏估计的均方根误差即标准差,反映了模型参数估值与真值之间的差异。有偏估计情况下,标准差是均方根误差的组成部分,因此,采用标准差进行分析更直观明了,两相邻正则化参数下的标准差变化可表示为

(15)

2.2.2 两正则化参数下的偏差相对变化量确定方法

在模型参数真值未知的情况下,无法准确可靠地对偏差进行直接计算。但是,通过计算两正则化参数下的均方根误差相对变化量,可消除参数真值未知的影响。由式(3)可得两正则化参数下均方根误差相对变化值向量为

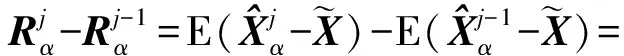
(16)

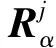
(17)

由此可得两正则化参数下的均方根误差变化量近似为

(18)

式中,rj为均方根误差变化量。由式(18)可知,均方根误差变化量近似等同于参数估值变化量。因而,正则化参数变化引起的模型参数估值变化量应受标准差变化与偏差变化的共同影响。设偏差变化影响量为pj,则参数估值变化量可表示为

rj=sj+pj

(19)

偏差为0时,参数估值变化仅受标准差变化影响,则参数估值变化量近似于标准差变化量,因此,在参数估值变化量差异于标准差变化量时,均可认为受到了偏差影响。则偏差变化影响量可近似计算为

pj=rj-sj

(20)

2.2.3 正则化参数确定方法

无偏估计的参数估值中不包含偏差,参数估值方差即均方误差,标准差即均方根误差。若正则化法引入的偏差为0,则等价于无偏估计,参数估值变化仅受标准差变化影响。因此,在标准差变化量确定的情况下,若模型参数估值变化量与标准差变化量相近,则正则化参数变化引起的偏差变化较小;如果参数估值变化量与标准差变化量差异较大,则正则化参数变化引起的偏差变化较大。

最优正则化参数可实现均方误差的最大降幅。由式(20)可知,两正则化参数间的模型参数估值变化量近似等价于标准差变化量与偏差变化量之和。即参数估值的变化受到标准差下降以及偏差增长的综合影响。正则化模式下,标准差随着正则化参数的增大而下降,偏差则随着正则化参数的增大而增长。尽管依据式(20)仅可得到近似的偏差增加量,但在标准差变化量已准确确定的情况下,如若参数估值变化量小于2倍的标准差下降量,则标准差下降引起的参数估值变化要大于偏差增加引起的变化,因此可认为标准差的下降量大于偏差的增长量,正则化参数的增大可降低均方误差。而如果模型参数估值变化量大于等于2倍的标准差变化量,则标准差下降引起的参数估值变化要小于偏差增加引起的变化,即标准差的下降量小于偏差的增长量,那么正则化参数的增大不能降低均方误差。利用两正则化参数下的参数估值变化与标准差变化,可间接实现偏差的相对比较分析,进而确定出两正则化参数中更利于降低均方误差的正则化参数。因而可得确定出两正则化参数中的较优正则化参数后,通过减小搜索步长,缩小搜索区间,可迭代计算得到最优的正则化参数。最优正则化参数确定过程如图1所示。

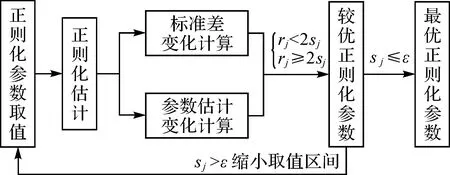
图1 正则化参数确定流程 Fig.1 Flowchart of regularization parameter determination

(21)

确定正则化参数的具体步骤如下:

(1) 选取正则化参数上下限及对比步长(例如0～10,步长为1),在上下限内不同正则化下进行正则化估计,得到模型参数正则化估值。

(2) 计算上下限内两相邻正则化参数下的标准差变化量及模型参数估值变化量,判断此正则化参数取值区间内的较优正则化参数。

(3) 以较优正则化参数为中心,以左右步长为上下限缩小搜索区间,而后降低搜索步长,重复上述步骤,通过迭代计算得到最终的最优正则化参数。

由于正则化参数是一个连续变量,两正则化参数区间内包含无穷多个正则化参数,选取一个较小的标准差变化量ε作为迭代终止条件,即在两正则化参数间标准差变化量sj≤ε时迭代终止。标准差变化量较小时,正则化参数变化所能降低的均方误差也较小,对模型参数估值的影响可忽略,因此,可认为确定的正则化参数已满足实际需求。

3 PolInSAR植被高度测量试验

极化干涉合成孔径雷达(polarimetric interfero-metric synthetic aperture radar,PolInSAR)通过多极化微波穿透观测,可有效采集植被覆盖区地表散射及植被体散射观测信息,实现大范围植被高参数及地表参数的反演,是大地测量中近年来新兴的具备穿透测绘能力的热门测量技术,并已广泛应用于大范围植被高度及林下地形的测绘[33-34]。然而,基于相干散射模型的PolInSAR模型参数反演存在病态问题,导致模型参数估计稳定性较差,严重影响了植被高等参数的反演精度[7,35]。因此,合理解决参数反演病态问题,是提高植被高参数反演精度与稳定性的关键。

3.1 试验一

为了验证本文算法在实际应用中的可行性与有效性,选取了欧空局AfriSAR2016项目获取的P波段全极化PolInSAR数据进行植被高参数反演试验,观测数据信息见表1,项目试验区位于非洲加蓬的Mabounie地区,该地区为典型的非洲热带森林,森林高度为40～50 m,森林茂密,地形复杂,常规测量技术难以实现大范围森林高度与林下地形的测量。

表1 数据采集信息

相干散射模型是描述雷达波信号在植被覆盖区散射传播过程的物理模型,是采用PolInSAR多极化观测数据反演植被高参数的基础。其中随机地体二层散射(RVoG)模型已广泛应用于不同类型植被高反演中,是目前应用效果最优的散射模型,该模型合理建立了植被参数与多极化观测量之间的函数关系[33]。具体表示为

(22)

式中,ω为极化向量,代表了不同极化状态;γ(ω)表示对应于极化向量ω的复相干观测,为已知观测量;φ0代表地表相位,为未知模型参数;μ(ω)表示地体幅度比,同样为未知模型参数;γv代表纯体相干性,其表达式中包含植被高参数,具体表示为

(23)

式中,σ为消光系数,为未知物理参数;θ代表雷达入射角,为已知参数;hv表示未知植被高参数;kz为垂直向有效波数,可通过已知参数计算得到。极化观测γ(ω)与纯体相干性γv均以复数表示。由RVoG模型可构建平差函数模型

γ(ω)=f(φ0,σ,hv,μ(ω))

(24)

为增加多余观测数,本次试验采用opt1、opt2、opt3、HH、HV、VV、PDHigh、PDLow、HHpVV、HHmVV共10种极化状态观测数据,进行植被高参数估计。由函数模型得到的G-M模型共包含植被高、地体幅度比等13个未知模型参数,其方程系数矩阵奇异值情况见表2。

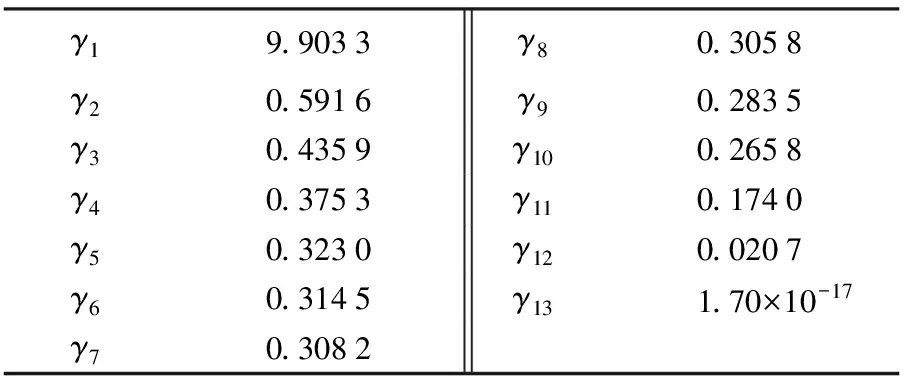
表2 观测方程系数矩阵奇异值

由表2可知,观测方程设计矩阵存在严重病态性,需利用正则化方法进行解算以改善参数估计质量。图2展示了本文方法确定正则化参数过程,试验中综合考虑标准差变化对模型参数估值变化影响及模型参数的实际大小情况选取ε为0.000 5,该条件下标准差继续下降,对模型参数估值精度提升已可忽略。由图2可知,在虚线处正则化参数为2×10-5时,参数估值变化量为0.07,标准差变化量为0.000 4,表明偏差增加引起的参数估值变化远大于方差下降影响,即偏差增加远大于方差下降,不利于均方误差的下降。而正则化参数为1×10-5时,标准差下降量远大于参数估值变化量,表明偏差增加量要远小于方差下降量,可大幅降低均方误差,因此,本文方法确定的正则化参数为1×10-5。为了对比分析,同时采用GCV法、L曲线法及均方误差最小法确定正则化参数并获得植被高参数估计结果。图3给出了各方法的植被高参数反演结果。

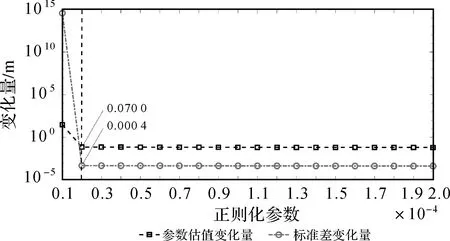
图2 相邻正则化参数间的模型参数估值变化与标准差变化Fig.2 Parameter estimate changes and standard deviation changes between adjacent regularization parameters

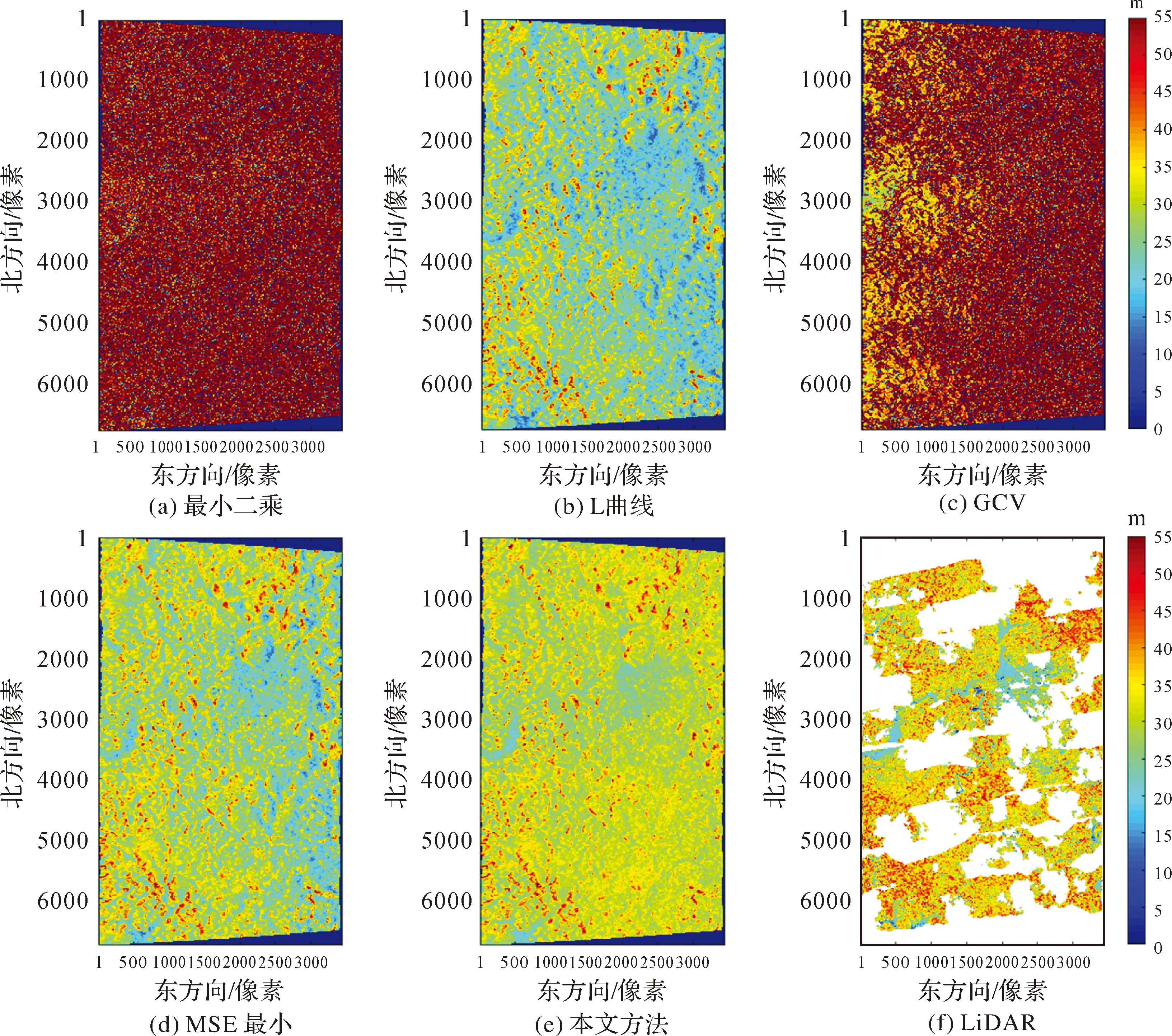
图3 PolInSAR穿透测量植被高参数反演结果Fig.3 Vegetation height inversion results of PolInSAR surveying

LiDAR技术具有较高的测量精度,其反演的植被高精度要远高于PolInSAR。因此,本试验中将LiDAR植被高结果作为参考值对比分析各方法PolInSAR植被高反演结果。图3(f)为NASA实施的LiDAR植被高测量结果,由于LiDAR与PoLInSAR飞行轨道不同,导致测量覆盖区域存在一些差异,此外,由于LiDAR测量易受云雾与天气变化影响,部分测量区域未能成功反演出植被高度,相较于PolInSAR结果出现部分缺失,但图中多数区域植被高反演结果可作为参考值进行对比分析。由图3(a)可知,受模型病态性影响,最小二乘估计已无法得到参数的有效估值,参数估计结果与LiDAR反演结果严重不符。图3(b)—图3(e)为采用正则化方法解算后的结果。对比可见,图3(c)采用GCV法确定正则化参数,其植被高反演结果与最小二乘结果相近,表明CGV法未能有效改善模型病态性影响。图3(b)、(d)、(e)植被高反演结果相比于最小二乘与GCV法有显著改善,其中图3(e)本文方法确定正则化参数的正则化法植被高参数估计结果直观上更接近于LiDAR反演结果,图3(d)均方误差最小法次之,图3(b)L曲线法相对较差。由此可知,本文方法确定的正则化参数,可改善正则化法模型参数估计结果。

为了量化分析各方法参数估计精度,依据LiDAR植被高反演情况,在图中均匀选取样地共1170块,用于统计分析植被高参数的反演精度,统计结果如图4所示。

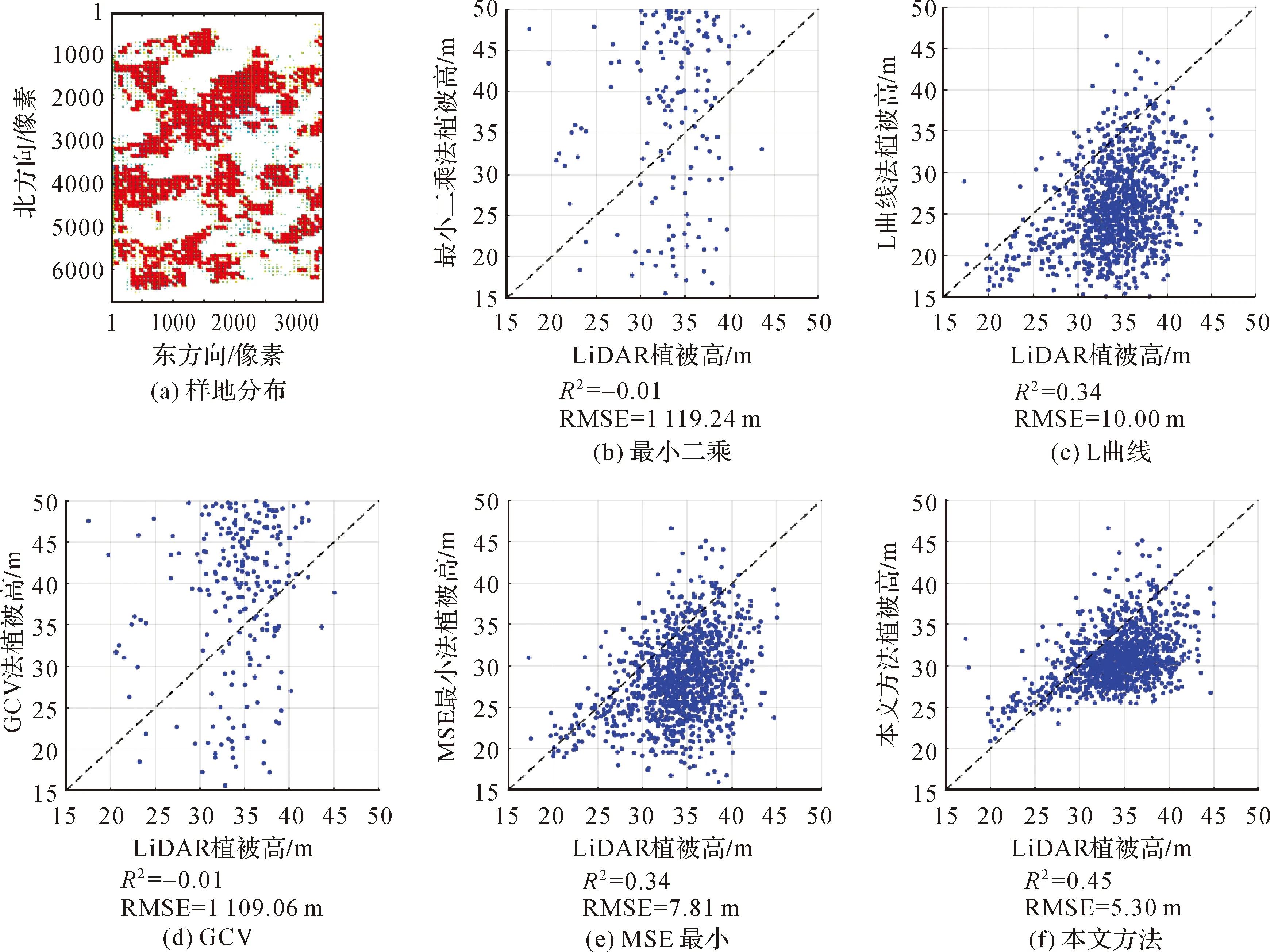
图4 PolInSAR穿透测量植被高参数反演误差Fig.4 Vegetation height parameter inversion errors of PolInSAR

图4反映了各方法的植被高参数估计误差统计情况。其中,图4(a)反映了用于统计分析的样地分布情况,图中红色区域为所选样地,依据LiDAR植被高反演结果,避开无数据区域,共均匀选取了1170块样地。由图4(b)与图4(d)可知,最小二乘估计与GCV法确定正则化参数的正则化法植被高反演均方根误差较大,均未能有效反演出植被高参数。图4(c)、(e)、(f)分别为利用L曲线法、均方误差最小法及本文方法确定正则化参数的植被高参数反演结果,由图4可知,3种方法均有效抑制了模型病态性影响,植被高参数估值均方根误差得到了显著降低。其中,图4(c) L曲线法确定正则化参数的正则化法植被高反演均方根误差最大,图4(e)均方误差最小法次之,图4(f)本文方法最小。本文方法相较于L曲线法,植被高反演均方根误差下降了47%,相较于均方误差最小法,均方根误差下降了32%。在相关系数R2上,本文方法较前两者也均有所提高。因此,采用本文方法确定正则化参数,在提高正则化法模型参数估计精度方面是可行且有效的。

3.2 试验二

试验二选取了德国宇航中心BioSAR2008项目采集的P波段全极化PolInSAR数据,观测数据信息见表3,项目试验区位于瑞典北部Krycklan地区,该地区植被类型为北方混交森林,地形复杂,森林高度为20～30 m,与试验一环境差异较大。

表3 数据采集信息

为便于验证分析,采用与试验一相同的反演策略进行植被高度反演,G-M模型设计矩阵奇异值情况见表4。

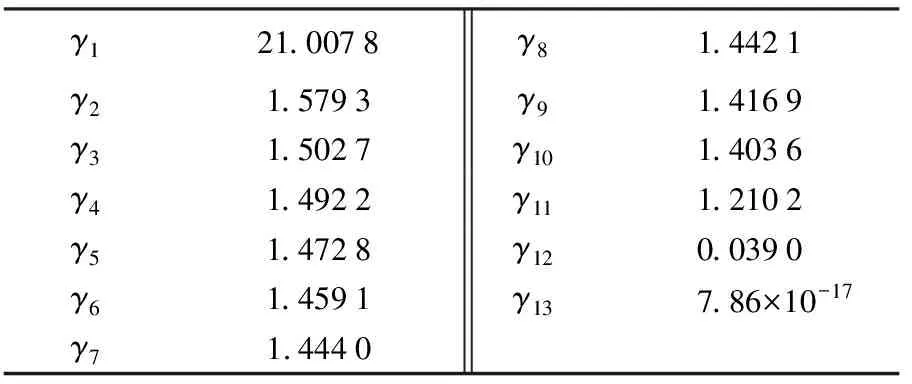
表4 观测方程系数矩阵奇异值

由表4可知,观测方程设计矩阵存在严重病态性。图5展示了本文方法确定正则化参数的过程。选取ε为0.000 5,即标准差变化量小于0.000 5时,对模型参数估值的影响已可忽略。由图5可知,在虚线处正则化参数为0.033时,参数估值变化量与标准差变化量分别为0.002 4和0.001 3,可见模型参数估值变化量略小于两倍的标准差变化量,即偏差增加量近似于标准差下降量。继续增大正则化参数则不利于均方误差的下降,因此本文方法确定的正则化参数为0.033。图6给出了各方法的植被高参数反演结果。

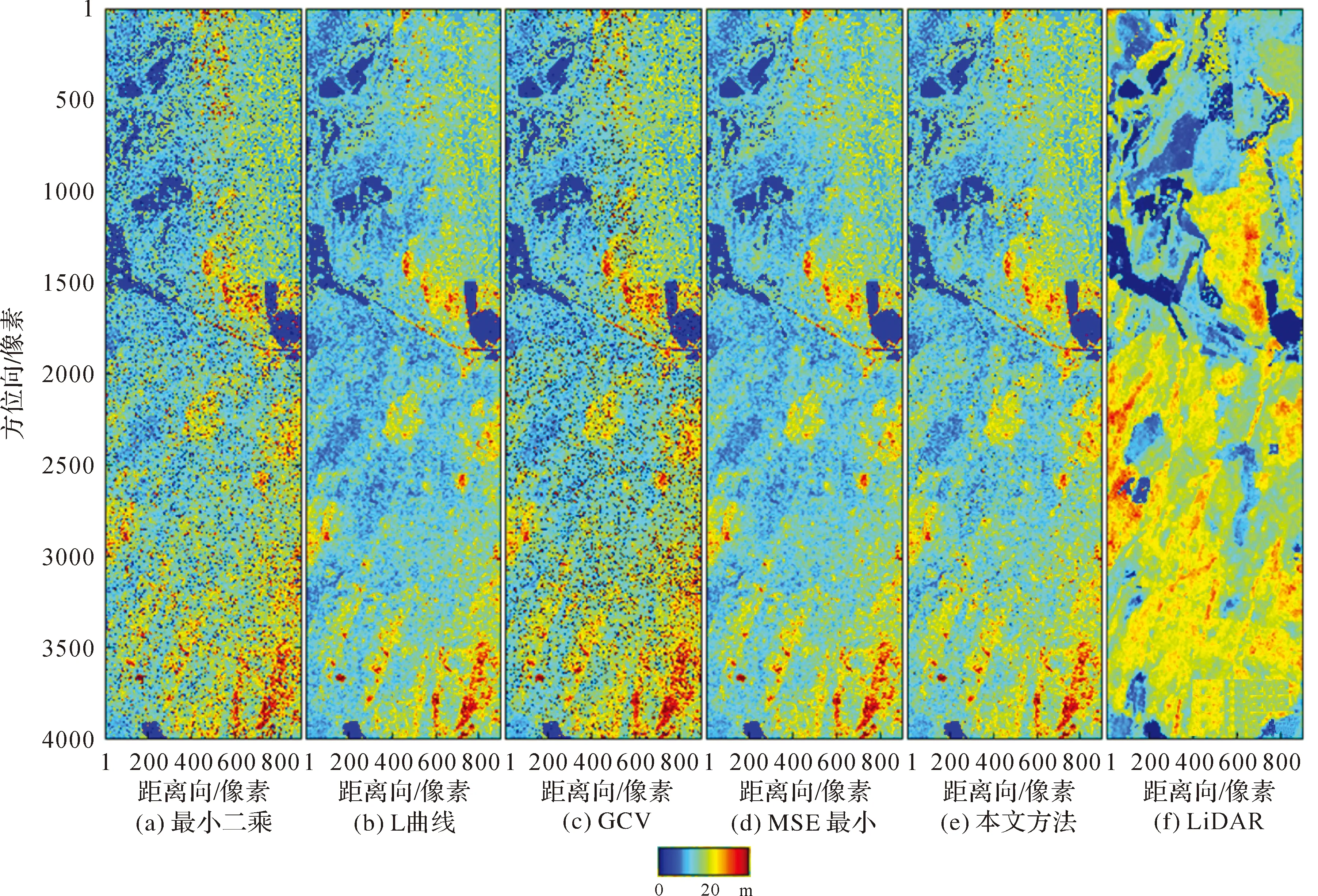
图6 PolInSAR穿透测量植被高参数反演结果Fig.6 Vegetation height inversion results of PolInSAR surveying

由图6(a)可知,受观测模型病态性影响,常规最小二乘估计方法已无法得到可靠的模型参数估值,部分参数估值严重失真。图6(b)、(c)、(d)、(e)为采用正则化方法解算后的结果,对比图6(f) LiDAR植被高结果可知,图6(c)采用GCV法确定正则化参数,其正则化处理未能有效地改善模型病态性,植被高参数反演结果与最小二乘估计相近。图6(b)、(d)、(e)分别采用L曲线法、均方误差最小法及本文方法确定正则化参数,植被高反演结果有显著改善,从色差上看,图6(e)结果略优于图6(b)和图6(d)。由此表明本文方法确定正则化参数时的正则化法模型参数估计结果最优。为了量化分析各方法参数估计质量,依据LiDAR植被高结果,在图中均匀选取样地共1326块,而后统计分析各方法植被高参数反演精度,具体统计结果如图7所示。

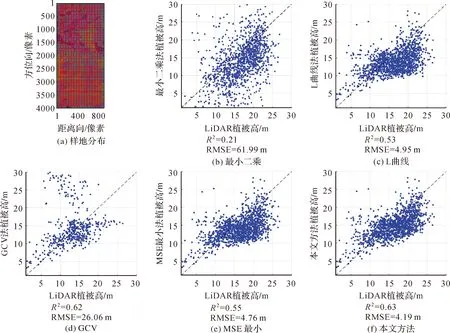
图7 PolInSAR穿透测量植被高参数反演误差Fig.7 Vegetation height parameter inversion errors of PolInSAR

图7(a)展示了依据LiDAR植被高结果所选取的样地分布情况,1326块样地均匀分布于全图区域。由图7(b)与图7(d)可见,最小二乘估计与GCV法正则化估计已无法给出可靠的参数估值,均方根误差较大且相关系数较低。图7(c)、(e)、(f)分别为L曲线法、均方误差最小法及本文方法植被高正则化估计结果,三者相比于最小二乘估计,植被高参数估值均方根误差得到了显著降低。其中,图7(f)本文方法均方根误差最小且相关系数R2最高,相较于L曲线法,植被高反演均方根误差下降了15%,相较于均方误差最小法,最高均方根误差下降了12%。因此,采用本文方法确定正则化参数可一定程度上提高模型参数正则化估计精度。

4 结 论

病态问题广泛存在于地球重力场反演,GNSS空间环境监测、InSAR地表监测等大地测量研究领域,严重影响了地球参数的反演精度与稳定性。常用的正则化解算方法可有效减弱病态性影响,改善物理参数的反演精度。然而,决定正则化方法参数反演结果的正则化参数,目前仍没有稳定最优的确定方法,导致选择不同正则化参数得到的模型参数估计结果相差甚远。鉴于此,本文通过分析正则化参数变化引起的方差与偏差变化规律,提出了一种均方误差相对比较方法,得出了以下几点结论:

(1) 基于不同正则化参数下的模型参数真值保持不变特性,通过计算不同正则化参数下的方差与偏差相对变化量,可消去参数真值,从而消除模型参数真值无法获取对偏差计算的影响。

(2) 利用不同正则化参数下标准差变化量与偏差变化量对模型参数估值的影响关系,可在模型参数估值变化量中去除标准差变化量影响,从而得到偏差相对变化量估值。

(3) 综合标准差相对变化量与偏差相对变化量对均方根误差的影响,可有效确定出均方误差最大降幅下的正则化参数。

(4) 通过PolInSAR植被高测量试验对本文方法的有效性与实用性进行了验证。试验结果表明,本文方法可有效改善正则化法模型参数估计精度。在不同场景PolInSAR植被高测量试验中植被高反演精度均得到了提高,有效验证了本文方法在实际应用中的合理性与可行性。