铁氧体磁芯磁场分布的优化及其对磁纳米热疗的影响
汤云东,陈泓霖,高跃明
(福州大学 物理与信息工程学院,福建 福州,350108)
磁纳米热疗相比传统热疗方法具有毒副作用低、靶向性好、对生物体影响较小等优点,已成为近年来最有潜力的肿瘤治疗手段之一[1-2]。此外,磁热疗还可以作为辅助手段与其他常规治疗方式,如化疗、药物治疗及免疫疗法等[3-5]进行联合最终提高治疗效果。磁热疗的基本原理是在外加交变磁场的作用下,注入肿瘤区域内的磁纳米粒子(magnetic nanoparticles, MNPs)产热,致使癌细胞因高热敏感性凋亡同时不损伤健康组织的治疗方法[6-8]。因此,治疗温度的有效控制是磁热疗最为关键的环节,而理想的治疗温度一般为42~46 ℃[9]。磁热疗期间治疗温度的决定性因素主要包括磁场和生物组织的特性、含MNPs的磁流体属性参数以及磁流体的注射策略等[10]。尽管以往的文献已经从不同方面对磁热疗进行了阐述,但治疗磁场的优化问题并未得到国内外学者较多的关注。
目前,用于产生磁热疗所需的交变磁场装置一般有通电螺线管[11]、亥姆霍兹线圈[12]以及缠绕载流线圈的铁氧体磁芯。理想情况下的治疗磁场应为均匀分布,但实际装置的磁场多为不均匀分布,而不均匀分布磁场会大大地影响磁热疗过程中的治疗效果[13]。为此,国内外学者不断地尝试改进磁场装置以期获得理想的磁场发生装置。RISTIĆ-DJUROVIĆ 等[14]为克服典型螺线管磁场均匀性较差的缺点,通过改变螺线管横截面的形状和尺寸从而减小磁场的变化,优化后的螺线管几何结构可实现最大的现场性能和最小的功耗,而且可保证获得最大磁感应强度时扩展螺线管尺寸,所提出的修改方法可将磁场均匀度变化减少10.6倍。LU等[15]则应用改进的3-s和四线圈结构对亥姆霍兹线圈体积均匀场进行优化,并通过有限元分析验证了所提归一化线圈参数公式的准确性,还通过实验验证了理论分析,揭示了改进后线圈可使功率损耗和导体质量显著下降,其性能也明显优于传统线圈。CHRISTIANSEN 等[16]提出一种小型交变磁场装置方案,该方案使用软铁磁芯将磁通集中到间隙中。然而,随着用于适应动物模型的实验空间增加,该装置的导热性变差,体积标度的堆芯损耗增加。尽管该装置也具有较好的应用前景,但研究中并未对这种装置提出有效的优化方法。NOMURA等[17]考虑铁氧体磁芯在产生磁场时由于涡流损耗、趋肤效应和邻近效应而造成的绕组损耗和磁芯损耗,并对磁体的热损失进行了评估,同时给出了热疗磁场装置可行性系统的主要参数。王世山等[18]推导了两类磁场在各自自由度下满足的微分方程,进而采用类比有限元法计算出铁氧体磁芯磁场的特征参数,求解了磁芯的等效电感和电阻等。尽管以往文献对各种装置磁场进行相应研究,但针对铁氧体磁芯磁场的优化和改进工作并没有获得足够的关注,而基于优化磁芯磁场的磁热疗研究仍需进一步探究。
因此,本文应用遗传算法对铁氧体磁芯的气隙长度和宽度等进行优化,使得气隙内磁场均匀度最优的同时保证磁场强度能让治疗温度处于临界值;进而采用有限元方法求解气隙磁场的偏微分方程,对磁芯线圈的位置进行优化设计,分析线圈处于不同位置时铁氧体磁芯磁场的等效磁路模型;最后,将优化后的气隙磁场应用于磁热疗的治疗温度模拟,并比较优化前后不同磁场对治疗效果的影响,在考虑了相应的初始条件和边界条件下,使用有限元方法对改进生物传热方程求解,预测生物组织治疗温度。
1 理论和方法
1.1 铁氧体磁芯磁场
以常见的带有载流线圈的铁氧体磁芯作为磁热疗交变磁场发生装置[16]。图1所示为磁场发生装置初始几何模型,该模型主要包括带气隙结构的铁氧体磁芯(蓝色)和套在磁芯上的载流线圈(黄色)。其中,铁氧体磁芯的高度为16 cm,宽度为12 cm,而磁芯上缠绕的线圈材料由金属铜构成。

图1 磁场发生装置的初始几何模型Fig. 1 Initial geometric model for magnetic field generator
铁氧体磁芯上的线圈加载交变电流时,磁芯间隙中会产生相应的交变磁场,由麦克斯韦方程组可知:
式中,∇为梯度算子;H为磁场强度;Ji为外加电流密度,可以认为是电磁场的来源;Jc为传导电流密度;Jc=σE,σ为媒质的电导率;E为电场强度;D为电位移矢量,D=εE,ε为媒质的介质常数;B为磁感应强度,B=μ0H,μ0为真空磁导率。
此外,根据Maxwell Faraday 方程,静止系统中的电场强度可以表示为
式中:A为磁矢势;ϕ为标量势,在本模型中不考虑聚集电荷,故假设其值为0。
将式(2)和式(3)代入式(1),并结合已知的关系式可以得到新的磁矢量势方程:
通过求解方程(4)可得到磁矢势A,并通过B=∇×A求解得到磁感应强度B,再依据B=μ0H可得出铁氧体磁芯内部和气隙空间中的磁场强度。
1.2 磁场作用下MNPs的产热
MNPs 置于铁氧体磁芯气隙中的交变磁场后,在交变磁场的作用下将产生用于肿瘤治疗所需的热量[19-20]。在粒径较小的情况下,MNPs产生的功率主要由弛豫损耗所决定,可表示为[21-22]
式中:P为功率;f为交变磁场的频率;χ″为复磁化率的虚部,
式中,ω为角频率,ω=2πf;χ0为平衡磁化率;τeff为MNPs的弛豫时间,
式中:τB为布朗弛豫时间;τN为尼尔弛豫时间;η为磁流体的黏滞系数;VH为磁流体粒子的流体动力学体积;kb为玻尔兹曼常数;T为热力学温度;τ0为平均弛豫时间;参数γ=KeffVm/(kbT),Keff为有效各向异性常数,Vm为MNPs 的体积,Vm=4πR3/3,R为MNPs的半径。
平衡磁化率χ0可以由下式表示:
式中:ξ为朗之万参数,ξ=μ0MdH0Vm/(kbT),Md为磁性颗粒的磁化强度;χi为初始磁化率,
式中:Ms为MNPs 的饱和磁化强度,Ms=ΓMd,Γ为MNPs的体积分数。
确定MNPs的产热情况后,生物组织的温升变化则可通过Pennes bio-heat transfer(PBHT)方程来预测。本文考虑了一种改进的PBHT方程[23-25]:
式中:i的值为0或1,分别表示健康组织和肿瘤组织;ρi,ci和ki分别为生物组织的密度、比热容和热导率;ρb,cb和ωb分别为血液的密度、比热容和灌注率;Tb为动脉血液温度;Qm为生物组织代谢热;α为校正系数,用于校正理论和实际情况下,不同溶液对MNPs产热影响的差异,一般取为0.55;QMNP为在交流磁场作用下磁纳米粒子在生物组织区域中产生的总热量。
QMNP与磁纳米粒子的空间浓度分布以及单个磁纳米颗粒在交变磁场作用下产生的热量有关,因此,QMNP=φ′(x,y,z)∙P,式中,φ′(x,y,z)为体积分数,用于说明肿瘤组织区域内的磁纳米粒子浓度分布。在本研究中,考虑肿瘤区域内的磁纳米粒子浓度分布为高斯分布,则φ′(x,y,z)可以表示为
式中,σ0为磁纳米粒子空间分布的方差,φ为磁纳米粒子的初始体积分数,σ0和φ分别取为20 和0.071;(x0,y0,z0)为磁纳米粒子的注入点,在本研究中定义为(0, 0, 0)。
1.3 铁氧体磁芯磁场优化方法
与螺线管和亥姆霍兹线圈相比,铁氧体磁芯产生的磁场容易实现相对较高的磁场强度,但同时也存在一定的不足[26],主要表现在:铁氧体工作时存在的磁滞损耗会引起铁氧体温度上升并增加额外的功耗;铁氧体磁芯气隙附近存在一定的磁通量分散,会导致气隙中磁场强度下降和磁场分布不均匀,而这些均会影响MNPs的产热,进而对热疗温度场的分布造成影响。其中,磁滞损耗与铁氧体中的磁通密度有关,而载流线圈位置则会影响铁氧体中磁通密度以及气隙中磁场强度。本文针对铁氧体磁芯磁场提出的改进方法如下:首先,应用磁路理论分析载流线圈处于不同位置时的等效磁路模型,同时使用有限元软件对不同的载流线圈位置进行仿真模拟;接着,对比仿真结果得出最佳的载流线圈位置后,将其应用到铁氧体磁芯中;最后,利用优化算法去进一步优化确定后的铁氧体磁芯气隙磁场,使磁场分布均匀程度最优以提高磁热疗的有效性。
为此,本文提出了一个用于评价磁场均匀性优化问题的不均匀性函数[27]:
式中:Hmax、Hmin和Hmean分别为铁氧体磁芯气隙区磁场强度的最大值、最小值和平均值。
此外,为提高治疗区域磁场的均匀性,采用遗传算法对不均匀性函数进行优化,优化算法中的待优化参数包括气隙两侧截面的铁氧体磁芯的长度和宽度等[28-31]。值得一提的是,遗传算法并不是本文研究的唯一可用算法,现有的诸多优化算法可能同样适用。然而,本文重点并不是关注优化算法导致的差异,故此处不展开讨论。
本文基于遗传算法的铁氧体磁芯磁场优化方法流程如图2所示,优化步骤可概述如下:
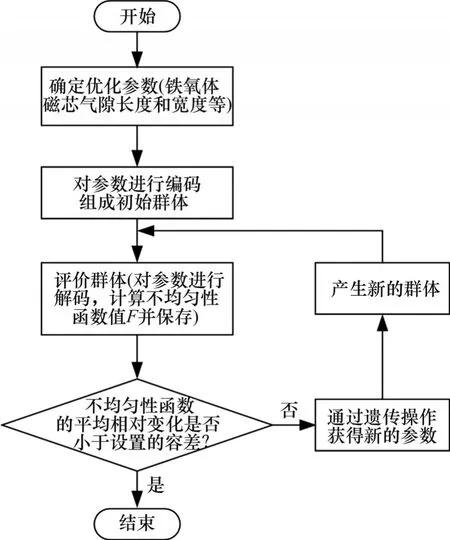
图2 优化过程流程图Fig. 2 Flow chart for optimization process
1) 将要使用的气隙两侧截面铁氧体磁芯的长度和宽度视为优化过程中的变量,并对它们进行二进制编码。每个变量的编码长度为10 之后通过随机函数在编码长度内随机生成0 或1,从而产生两组随机数作为算法中的初始群体;
2) 对群体中个体进行评价,包括对参数进行解码以及根据解码后的参数计算不均匀性函数F并保存;
3) 判断不均匀性函数F的平均相对变化是否小于所设置的函数容差(本文函数容差设置为10-6);
4) 若不满足所设置函数容差要求,则对群体进行遗传操作获得新的参数并产生新一代的群体;并再一次重复步骤2)和步骤3)直到满足函数容差要求,则算法停止迭代并结束优化。
优化算法迭代完成后将得到不均匀性函数F的最优值,同时得到最优化待优化参数(磁芯的长度和宽度)。同样地,在最优待优化参数作用下,铁氧体磁芯也将获得最均匀的磁场分布,将该最优磁场应用于磁热疗时可在肿瘤区域获得均匀的产热分布。
2 生物组织参数
2.1 常量参数
为了求解方程(5)中的功率P,参考文献[32-33]选取MNPs产热相关的参数,如表1所示,为求解改进的PBHT 方程即式(11),根据文献[33]选取生物组织特性参数,如表2所示。

表1 MNPs产热参数Table 1 Parameters for heat generation by MNPs

表2 生物组织特性参数Table 2 Parameters for bio-tissue characteristics
2.2 磁纳米粒子注入后的热特性
随着MNPs的注入扩散,改进的PBHT方程中考虑的肿瘤参数应同时包含MNPs和肿瘤组织。因此,注射后肿瘤混合区的生物组织特性参数可通过以下计算方法来描述[34]:
式中:下标tumor 和MNP 分别表示肿瘤和磁纳米粒子;ε为MNPs 注射进肿瘤区域后在该区域内所占的体积分数,其临床典型值为0.003[35]。
2.3 温度依赖性的血液灌注率
除了磁纳米粒子的注入会对生物组织特性参数造成影响之外,治疗期间温度的变化也会对其造成影响,其中,血液灌注率会随着局部温度的变化而改变。因此,为了使所计算的温度分布更加准确,本文将血液灌注率视为人体健康组织和肿瘤组织的局部温度的函数,其表达式如下:
式中:ω0b(T)和ω1b(T)分别为健康组织和肿瘤组织中受局部温度影响的血液灌注率。
3 结果和讨论
3.1 载流线圈位置对于铁氧体磁芯磁场的影响
铁氧体磁芯磁场跟线圈位置以及气隙特征等均相关,确定线圈的最优位置有利于气隙特征的优化。图3所示为线圈分别位于磁芯左端图和气隙两端时的铁氧体磁芯磁场模型。图3中,带隙的空心长方体表示磁芯,套在磁芯上的黄色圆环表示载流线圈,而气隙中的同心球则表示生物组织,同心球中灰色区域表示人体健康组织(半径150 mm),绿色区域表示肿瘤组织(半径100 mm)。
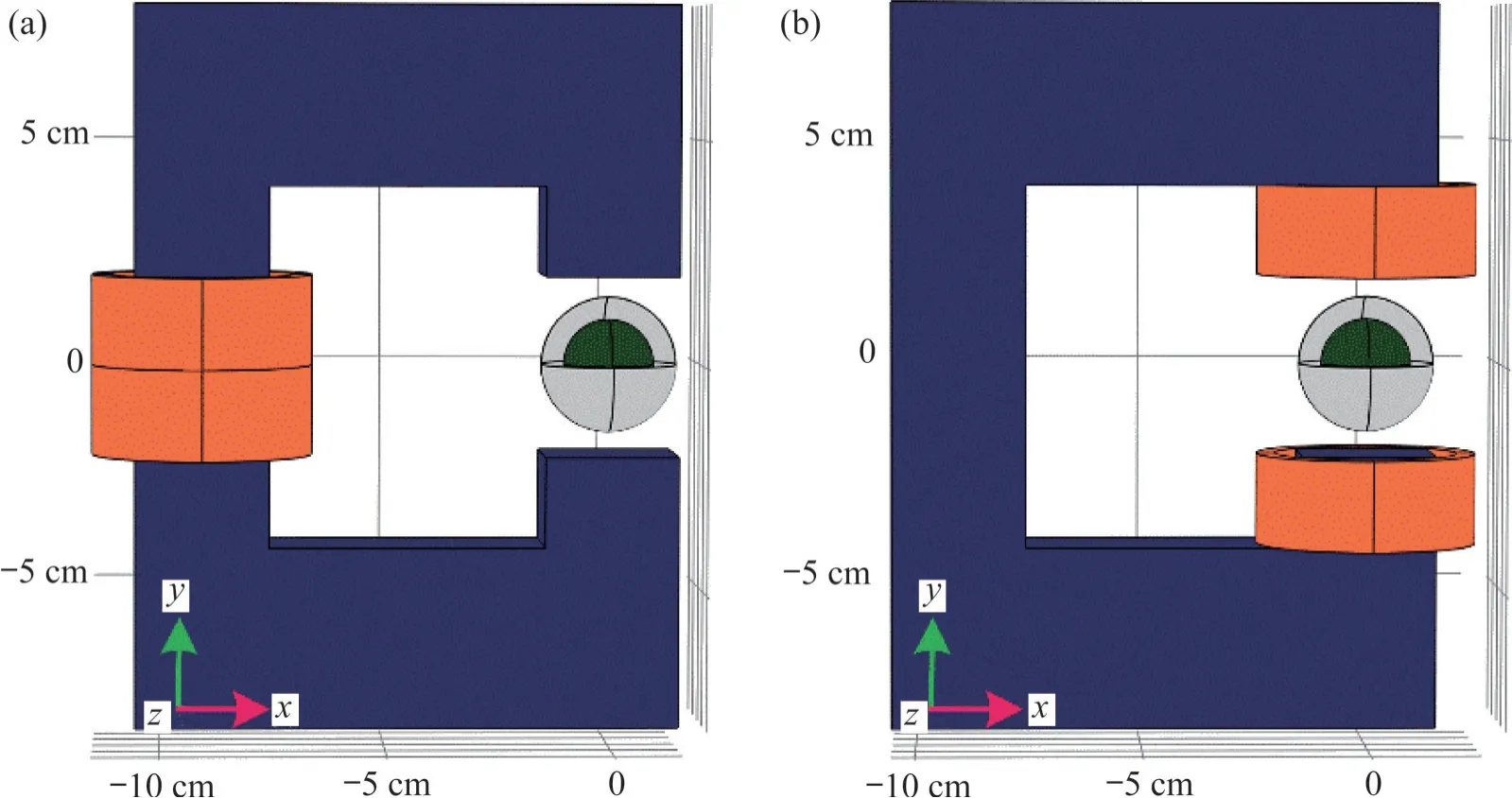
图3 不同线圈位置时的铁氧体磁芯磁场模型Fig. 3 Magnetic field model of ferrite core with different coil locations
运用磁路理论分析图3可得到如图4所示的磁路等效图,其中,载流线圈用磁动势表示,磁芯中各部分磁路用磁阻表示,NI∙sin(ωt)为线圈中的磁动势,Rg为气隙中的磁阻,Rl为磁芯上下两端之间的磁阻,Rm为磁芯左端的磁阻,Rl>Rg≫Rm。图4(a)中,Rg与Rl并联后再与Rm串联,故总磁阻可表示为Rm+Rl//Rg,图4(b)中,Rg直接与线圈相连,故总磁阻可等效为Rg+Rl//Rm。因此,2 种情况下的总磁阻并不相同,这也将导致磁芯中磁通密度分布以及气隙中的磁场强度不同。

图4 不同线圈位置时的等效磁路图Fig. 4 Equivalent magnetic circuit diagram with different coil locations
利用有限元方法对式(4)进行求解后,可得到相同电流下不同线圈位置时铁氧体磁芯磁场的分布,如图5所示。由图5可知:线圈位于气隙两端时的磁通密度比位于磁芯左端时的磁通密度更低,导致其磁滞损耗也更小;线圈位于气隙两端时的磁场强度比位于左端时的磁场强度更大,而这两者的差异见图5(e),其中,L1表示图5(c)对应的曲线,而L2 表示图5(d)对应的曲线。这也表明产生相同的磁场强度,线圈位于气隙两端时所需的功率会更小。因此,线圈在气隙两端优于在磁芯左端,能产生更有利于磁热疗所求的交变磁场。

图5 不同线圈位置的磁芯磁场分布Fig. 5 Magnetic field distribution for magnetic core with different coil locations
尽管如此,由图5(d)可知,气隙中磁场强度分布的均匀度并不理想,故本文采用遗传算法通过优化铁氧体磁芯多个参数来提高气隙中磁场强度分布的均匀度,从而提高磁热疗治疗的温度分布以及治疗效果。
3.2 铁氧体磁芯磁场的优化
铁氧体磁芯磁场的影响因素较多,主要包括磁导率、饱和磁通密度、电阻率、剩余磁通密度、矫顽力以及磁芯几何尺寸等。其中,磁导率和饱和磁通密度会影响铁氧体磁芯工作时产生的磁感应强度幅值,而电阻率、剩余磁通密度以及矫顽力则与铁氧体磁芯在磁化时所造成的能量损失有关。然而,本文主要关注气隙内磁场强度的均匀性,其与上述参数关联性并不大,但与铁氧体磁芯截面的长度和宽度密切相关。鉴于此,本文最终确定铁氧体磁芯截面的长度和宽度为遗传算法的优化参数,以线圈位于气隙两端情况为分析对象,采用本文所提优化方法对气隙两端参数进行优化,以期提高磁热疗装置的气隙磁场均匀性。
利用本文所提优化方法进行优化过程中,迭代变量和不均匀性函数F的收敛曲线如图6 所示,其中,图6(a)中的2个待优化变量分别为气隙两端对应的铁氧体磁芯截面的宽度(w)和长度(l)。从图6可以看出,在迭代400次前,迭代变量和不均匀性函数均出现较大的波动,而在迭代400次后,两者开始稳定并一直保持不变。且在收敛后不均匀性函数值从开始的0.8下降到了0.2左右。

图6 迭代变量和不均匀性函数的收敛曲线Fig. 6 Convergence curve of iterative variables and inhomogeneity function
确定最优参数后,铁氧体磁芯气隙中的磁场分布便可通过求解有限元方程(4)获得。
图7 所示为优化后气隙中磁场强度分布在x-y平面的切片图(z=0)。由图7可以看出,优化后,气隙中磁场强度分布的均匀度得到显著提高,特别是在气隙边缘区域优化尤其明显。为进一步阐明优化效果,图8 所示为优化前后气隙中不同位置x轴截线的磁场强度变化曲线。由图8(a)可知,气隙区域内优化前磁场强度最大值在9 kA/m 左右,而最小值则在5.5 kA/m 左右,两者相差达3.5 kA/m;优化后,磁场强度最大值和最小值的差异减小到1.5 kA/m 以内,气隙内磁场均匀度得到明显提升。因此,也证明了本文所提优化方法的有效性。

图7 优化后x-y平面磁场强度分布Fig. 7 Magnetic field intensity distribution in x-y plane after optimization

图8 优化前后不同位置的x轴截线的磁场强度变化曲线Fig. 8 Magnetic field intensity curve for x-axis crosssection at different positions before and after optimization
3.3 优化前后磁场对于热疗温度场的影响
气隙内磁场优化完成后,通过求解方程(11)便可获得生物组织的温度分布。磁热疗过程中,合适的治疗温度范围(42~46 ℃)可以使癌细胞凋亡同时不损伤健康组织,本文以肿瘤区域内有效温度体积百分比(effective temperature percentage inside tumor, ETPIT)来评估治疗效果。图9所示为相同电流下不同磁场作用下生物组织区域的稳态治疗温度分布结果。由图9可知,优化后磁场下,治疗温度整体上升,其治疗区域最高温度从未优化磁场下的44.5 ℃升至46 ℃,整体治疗温度显著上升,同时,评估参数ETPIT 也从46.76%升至优化后磁场下的88.95%。

图9 生物组织区域的治疗温度分布Fig. 9 Treatment temperature distribution for bio-tissue region
由式(11)可知,治疗温度最大值实际上主要取决于MNPs的产热功率,因此,优化前的气隙磁场分布通过对线圈电流进行穷举法多次尝试也可使得治疗区域最大值指定为临界治疗温度(46 ℃)。为了进一步揭示优化前后磁场均匀性对治疗温度分布影响的差异,本文应用穷举法人为多次尝试将线圈电流设定为10.8 A后,可获得未优化磁场装置下治疗区域温度最大值为46 ℃的组织温度分布。尽管调整后未优化磁场和优化后磁场分别作用下的生物组织区域最高温度相同,但这2种情况下的生物组织区域温度分布必然不同。在最大值均为46 ℃时,调整后未优化磁场和优化后磁场作用下的生物组织治疗温度差异分布如图10 所示。从图10可以看出,2种情况下肿瘤中心治疗温度均为最大值46 ℃,即中心及附近的温度差异基本为零。此外,随着距中心距离的增加,两者的温度差异变得明显,但沿着不同轴向并不对称,这主要由气隙内磁场的不对称性决定。总之,优化磁场作用下治疗温度整体更高,最大差值可达到0.5 ℃,故其治疗效果最佳。因此,本文所提气隙内磁场优化方法不仅能提高磁场分布的均匀性,也能使得磁热疗期间治疗温度分布整体更优。

图10 两种不同磁场作用下的治疗温度差异Fig. 10 Temperature difference under two different magnetic fields
4 结论
1) 在铁氧体磁芯磁场中,铁氧体磁芯线圈位于气隙两端比位于磁芯左端更优。
2) 利用遗传算法优化后,气隙中磁场强度分布的均匀性明显提高,气隙区域内磁场强度最大最小值差异从优化前的3.5 kA/m 左右迅速减少至1.5 kA/m以内。
3) 肿瘤区域内有效温度体积百分比从优化前的46.76%提高至88.95%,治疗效果显著提高。
4) 虽然通过穷举法提高线圈电流方式来提高MNPs产热值的方式可将有效治疗温度百分比也提高至79.82%,但总体的治疗效果还是较本文所提优化方式差;本文所提优化方式在提高肿瘤组织内温度分布均匀性(最大温差为0.5 ℃)的同时,还在一定程度上降低了线圈的输入电流。

