供水管网压力分区方法的比较分析
何立新,范一飞,雷晓辉,王 琦
(1.河北工程大学水利水电学院,河北 邯郸 056000;2.河北工程大学河北省智慧水利重点实验室,河北 邯郸 056038;3.广东工业大学土木与交通工程学院,广东 广州 510006)
随着城镇供水管网规模越来越大,城镇供水压力导致的漏损问题也在逐步恶化。供水管网压力分区是解决管网漏损的前提之一,其根据节点坐标及节点压力,将管网划分成多个区域,划分后各分区内节点相近,压力相似。对各压力分区进行不同的调控,可以有效降低整个管网压力,从而达到减少漏损目的[1]。
国内外许多学者也都基于各种目的,选取了不同数据集(如节点坐标、节点压力等)与方法对管网进行了分区。张伟倩[2]运用Canopy 算法确定分区个数后选择K 均值聚类算法对管网进行压力分区,将管网分成多个区域,并成功降低了整体压力。唐鹏翔[3]则利用广度优先邻居聚类算法,通过节点坐标与节点压力对管网进行分区,在压力调控中取得了较好的压力控制效果。Herrera 等[4]将管网的拓扑结构和水力平衡作为约束条件,通过谱聚类算法对管网进行分区,实现了管网漏损控制。Paola 等[5]在分区时以压力、流量和运行费用为数据集,利用K均值聚类算法制定了DMA分区方案。刘俊等[6]则证明了谱聚类算法在供水管网中的有效性。
本文选取K均值聚类算法、层次聚类算法、谱聚类算法3 种常用的分区方法在Anytown 和KY3 2 个典型管网案例中进行了应用,通过轮廓系数来选取各方法在各管网案例中的最佳分区方案。通过对结果的比较分析,确定适应度较广的聚类分区方法,为供水管网压力分区提供参考。
1 计算分区方法
1.1 K均值聚类算法(K-means)
K均值聚类算法是一种矢量量化方法,也是无监督学习领域最为经典的算法之一。其起源于信号处理,是数据挖掘中常用的聚类分析方法。K均值聚类算法将n个数据点进行聚类分析,得到k个聚类,使得每个数据点到聚类中心的距离最小。具体步骤如下。
(1)给定数据集X={x1,x2,···,xn}。
(2)从数据集中任意选取k个对象作为初始聚类中心,并从X中将其取出。
(3)采用下式分别求出各元素到初始聚类中心的距离,并将元素分配至最靠近的初始聚类中心,将数据分为k类。
式中:dist()Xi,Cj为样本Xi到聚类中心Cj的距离;Xi为样本数据(i=1,2,3,…,n),Xi,t为第i个样本数据的第t个要素;Cj为聚类中心(j=1,2,3,…,n),Cj,t为第j个聚类中心的第t个要素;m为数据维度;t为数据的第t个要素。
(4)根据下式重新计算k个新聚类中心点,并重复步骤(2):
式中:Centerk为新聚类中心;| |Cj为第j个聚类中所包含的样本个数;xi为属于Cj聚类中心的样本。
(5)直到更新后的聚类中心和上一次的无变化或误差平方和最小停止迭代。
1.2 层次聚类算法(Hierarchical clustering)
层次聚类算法是从N个簇开始,将每一个对象作为一个簇,然后在每个步骤中合并2 个最相似的簇,直到形成一个包含所有数据的簇。具体步骤如下。
(1)每个数据点被指定为单个簇。
(2)确定距离测量值并计算距离矩阵,一般采用欧几里得距离,公式如下:
式中:ρ为欧几里得距离;x1、y1、z1为第一个点内要素;x2、y2、z2为第二个点内要素。
(3)确定合并簇的链接条件。链接条件有以下4 种:①最远邻聚类,计算簇与簇之间各元素距离,将最远距离作为簇与簇的距离;②最近邻聚类,计算簇与簇之间各元素距离,将最近距离作为簇与簇的距离;③平均链接聚类,计算簇与簇之间各元素距离,将平均距离作为簇与簇的距离;④最小化所有簇内的平方差总和。
(4)更新距离。
(5)重复这个过程,直到形成包含所有数据的N个簇(N为需要的簇的个数)。
1.3 谱聚类算法(Spectral clustering)
谱聚类算法是基于图论的算法,是将样本点两两相连构成图这一数据结构。谱聚类是通过切图的方式来划分不同的簇,其原理是使得子簇内部边的权重之和尽可能高,而不同子簇之间边的权重之和尽可能低。具体步骤如下。
(1)给定数据集X={x1,x2,···,xn}。
(2)使用下式计算n×n的相似度矩阵W:
式中:wij为相似矩阵W中第i行第j列元素;xi为数据集X 中第i个元素;xj为数据集X 中第j个元素;σ为高斯滤波器宽度;n为数据集中数据个数。
(3)将相似矩阵W 中的每行元素之和构成n×n对角阵,也就是度矩阵D,由下式计算:
式中:di为度矩阵D第i行第i列的元素;wij为相似矩阵W的第i行第j列元素。
(4)计算拉普拉斯矩阵L=D-W。
(5)计算L 的特征值,并将特征值由小到大排列,计算前k个特征值的特征向量,组成矩阵U={u1,u2,···,uk},U ∈Rn*k。
(6)令yi∈Rk是第i行向量,其中i=1,2,···,n。
(7)使用K-means算法将新样本点Y={y1,y2,···,yk}聚类成簇C1,C2,···,Ck。
2 评价指标
由于K均值聚类算法、层次聚类算法、谱聚类算法均需要提供簇的个数,为确定最优的簇的个数,采用轮廓系数对2到n个分区进行评价,从中选出最优簇的个数。
轮廓系数是评价聚类算法性能的一个指标。使用单个簇的紧凑性(簇内距离)和簇间的分离(簇间距离)来衡量聚类算法执行情况的得分,其范围在[-1,1]。S值越大,越合理。其计算公式为:
式中:S(i)为每个点的轮廓系数;a(i)为点i到簇内其他点的距离的平均值,体现凝聚度;b(i)为点i到其他簇中所有点的距离的平均值中的最小值,体现分离度;S为该聚类的轮廓系数;n为点的个数。
3 结果与分析
3.1 管网案例分析
选取了2 个管网进行分区方法比较,其中Anytown 是一个节点较少、拓扑结构相对简单的供水管网,而KY3 则是一个节点数较多、拓扑结构相比于Anytown复杂的供水管网。
Anytown 来自一个假设的社区供水系统。供水系统如图1(a)所示,该系统为环形管网,拥有1个水源、2 个水池、3 个水泵、16 个节点。管网高程东高西低。
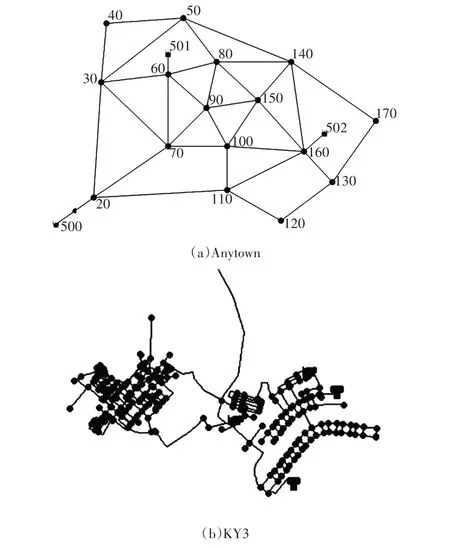
图1 管网案例
KY3来自一个位于肯塔基州供水系统。供水系统如图1(b)所示,该系统为环形管网,拥有3 个水源、3 个水池、5 个水泵、269 个节点。管网高程西边部分呈南高北低,东边部分呈南低北高。
3.2 不同分区方法最佳分区个数比较
根据评价指标,分别计算Anytown 和KY3 在3种分区方法下的最佳分区,数据集为节点坐标和各节点压力。考虑到管网规模以及分区成本,Anytown分区个数限制在2~4 个,KY3 分区个数限制在4~8个,具体流程如图2所示。
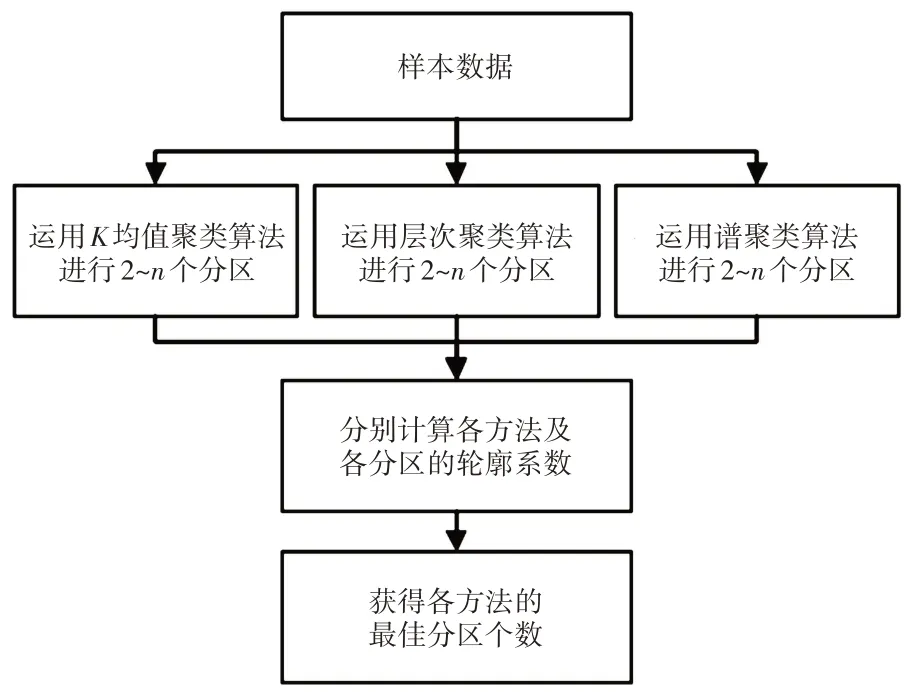
图2 分区方法流程比较
3.2.1 Anytown模型
通过评价指标,得到Anytown在3种分区方法下各分区个数的轮廓系数,详见表1。
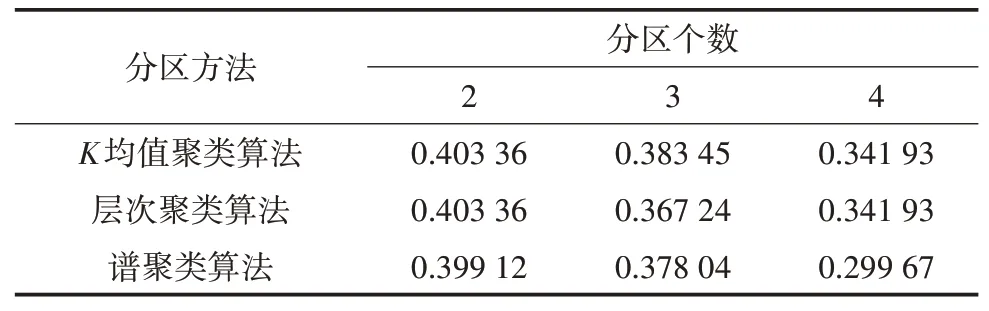
表1 Anytown分区结果的轮廓系数
由表1 可知,3 种方法的最佳分区个数均为2个,且K均值聚类算法和层次聚类算法2 种分区方法的评分高于谱聚类算法。3 种分区方法的结果及各节点压力如图3 所示,图3(b)(c)(d)中黑色节点代表在同一分区内,灰色节点代表在不同分区内。
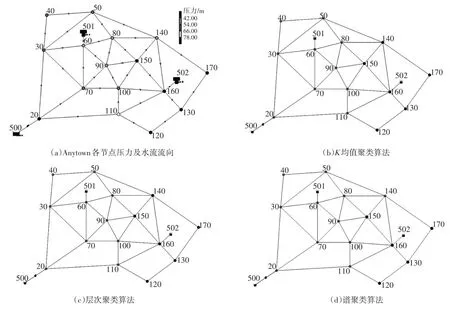
图3 Anytown各节点压力与分区示意
通过图3可知,K均值聚类算法和层次聚类算法的分区是相同的,与谱聚类算法仅是“140”节点不同,通过节点压力图可以发现该节点压力与左侧接近,但距离接近“150”节点。通过水流流向可以发现“110”节点是东侧分区的一个入口,无法直接打断,会在进行分区时进行适当调整。对于Anytown 管网来说,K均值聚类算法和层次聚类算法计算效果比谱聚类算法好。
3.2.2 KY3模型
通过评价指标,得到KY3 在3 种分区方法下各分区个数的轮廓系数,详见表2。

表2 KY3分区结果的轮廓系数
由表2 可知,K 均值聚类算法最佳评分分区为7,层次聚类算法最佳评分分区为8,谱聚类算法最佳评分分区为6。3 种分区方法的结果及各节点压力如图4 所示,图4(b)(c)(d)中同一种颜色则代表节点在同一分区内。
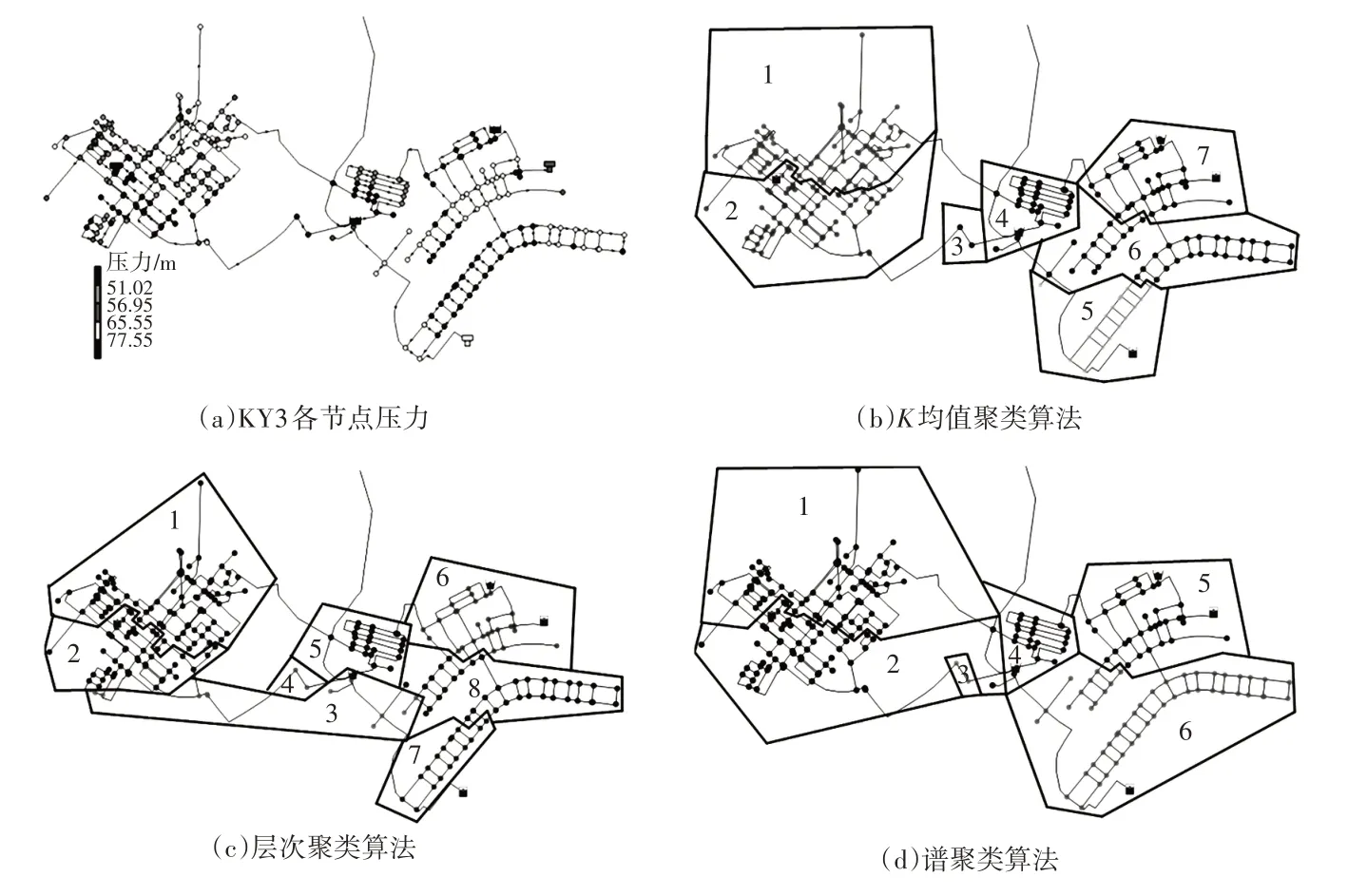
图4 KY3各节点压力与分区示意
通过图4 可知,K均值聚类算法不管是在节点坐标还是在节点压力上区域间都较为分明。层次聚类算法从节点坐标上看则稍有瑕疵,如3 号区域节点相距比较分散。谱聚类算法也在节点坐标方面存在瑕疵,如2 号区域节点有部分被分离在了较远且没有管网相邻的位置。3 种算法均出现了由于距离相近压力相近却不链接的节点分在同一区域,均需要在进行压力分区时进行手动修改。
4 结论
(1)层次聚类算法在Anytown 简单管网下效果较好,但是在KY3 复杂管网中会出现节点分散。谱聚类算法虽然在Anytown 简单管网下会出现部分节点分区不恰当的问题,但在KY3 复杂管网中的分类效果要优于层次聚类算法。
(2)K均值聚类算法在Anytown 简单管网和KY3 复杂管网中的压力分区结果相较于其他2 种算法均具有较好的效果,在压力分区内没有较为分散的节点。
(3)由于3 种算法均无法考虑拓扑结构的问题,会导致距离相近和压力相近但没有链接的节点划分至同一个压力分区中,在实际进行压力分区时仍需要根据需要进行调节。

