基于多神经网络的综合能源系统用户侧冷热负荷预测模型

张文栋, 刘子琨

(五凌电力有限公司,湖南,长沙 410000)

0 引言

城镇化发展过程中,按照小区形式建立综合能源系统,实现区域建筑群同步化供冷供热的方式不断推广[1]。为了满足能源可持续化发展要求,用户侧冷热负荷预测是不可或缺的环节[2]。基于负荷预测结果,指导该区域综合能源系统的供给规划,有利于降低区域综合能源的消耗。

现有的冷热负荷预测模型并未从用户侧入手,预测结果精度较低,如何构建高精度负荷预测模型成为研究重点。文献[3]利用调整误差算法,根据区域历史天气信息预测天气情况,结合区域历史负荷数据,在遗传算法和BP神经网络的作用下,获取负荷预测结果,该方法在实际应用中获取的预测结果与实际数据相比误差较大。文献[4]以主成分分析方法为基础,对冷、热负荷的本征模态进行分解,获取降维后的特征数据。采用DBiLSTM 神经网络和MLR得到重构后的预测结果,但是该方法应用范围较小,拓展性较差。文献[5]采用k-means聚类方法将多种负荷像素,按照相关性进行重构。选取多通道卷积神经网络分析聚类处理后的负荷像素,提取负荷特征。最后,按照长短时记忆网络结合时序方法,得到高精度负荷预测值。但是,该预测方法稳定性较差。

对此,从用户侧角度进行研究,以多神经网络为基础,设计综合能源系统冷热负荷预测模型,极大程度上提升了负荷预测精度。

1 基于多神经网络的综合能源系统用户侧冷热负荷预测模型设计

1.1 分析综合能源系统的能量流

区域综合能源系统包括电力、热力和燃力3种子系统,通过转换设备使得每个子系统之间相连,系统内能量流如图1所示。

图1 含电、热、气的综合能源系统

基于图1,对热力系统进行研究,辅助用户侧冷热负荷的预测工作。热力系统中以水作为主要传输介质,热量从热源出发,随着温度较高的传输介质到达热负荷位置,经由散热器将热能传递至用户,直到温度降低到阈值,通过回热管道返回至回热源[6]。通过水力与热力分析热力系统能量流,其中水力能量流表达式为

(1)

式中,A表示节点关联矩阵,s表示供热网络的节点,m表示节点流出的流量,q表示节点数量,B表示回路关联矩阵,h表示供热管网的回路,f表示压头损失向量。其中,f计算式为

f=Km|m|

(2)

式中,K表示综合能源系统内管道的阻力系数矩阵。而综合能源系统热力能量流表达式为

(3)

式中,φ表示热力网络的节点热功率,C表示传输介质的比热容,T表示温度,Ts表示负荷之前的传输介质温度,To表示负荷之后的传输介质温度,Tend表示能源系统管道末端温度,Tstart表示管道始端温度,Ta表示管道周围环境温度,λ表示热导率,mout表示流出流量温度,min表示流入流量温度,Tout表示流出介质温度,Tin表示流入介质温度。

通过上述计算,得到区域综合能源系统的能量流分析结果,为后续负荷预测提供理论基础。

1.2 获取用户侧冷热负荷计算参数

冷热负荷预测是综合能源系统服务的基础,为了加强预测准确性[7],将冷热负荷的影响因素划分为两类参数。一部分是自有属性参数,包括用户侧建筑朝向、窗墙比以及热阻等固定参数;另一部分是运行属性参数,包括内部热源、人员安排等随时发生变化的数据[8]。

对用户侧冷热负荷预测时,将单位时间内房间冷负荷pα和热负荷pβ预测,二者应该满足:

(4)

式中,p1表示温差引起的用户侧热量传递,p2表示建筑吸收的太阳辐射,p3表示空气渗透热量,p4表示综合散热功率。依据国家标准传热学基本原理可知,p1满足:

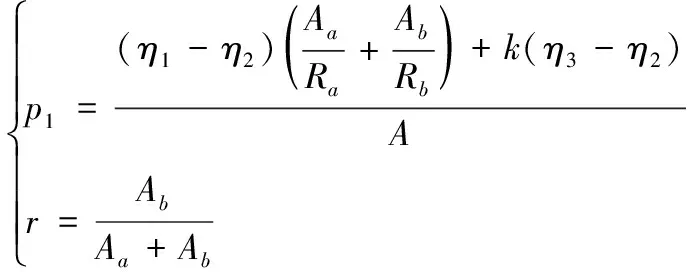
(5)

式中,r表示用户侧建筑窗户墙体比值,k表示地面综合传热系数,A表示用户侧空调面积,Aa表示外墙面积,Ab表示窗户面积,Ra表示外墙热阻,Rb表示窗户热阻,η1表示外界环境温度,η2表示室内温度,η3表示地表温度。建筑吸收的太阳辐射计算式为

(6)

式中,ε表示传热修正系数,θ表示平均传热系数,ϖ表示用户侧围护结构,g表示太阳辐射,θϖ表示用户侧围护结构的平均传热系数,θg表示太阳辐射的平均传热系数。空气渗透热量计算式为

(7)

式中,ρ表示空气比热容,N表示换气次数,V表示换气体积。综合散热功率计算式为

(8)

式中,l表示建筑单层高度,e表示室内设备密度,μ表示平均散热功率。

1.3 设计多神经网络预测方案

以冷热负荷预测的计算参数为基础[9],结合BP网络、RBF网络和小波神经网络,设计多神经网络预测方案。首先,将负荷计算参数输入3种神经网络内,获取用户侧冷热负荷预测结果[10]。采用非线性关系,分析3种神经网络预测结果相关性,得到误差平方和χ:

(9)

式中,∂表示样本个数,j表示非线性函数,i表示预测次数,fi是第i次的实际负荷值,f1i表示BP网络预测结果,f2i表示RBF网络预测结果,f3i表示小波神经网络预测结果。

将3种神经网络相结合形成多神经预测网络后,常规的遗传算法难以求解出预测结果。考虑到3层神经网络可以完成复杂非线性映射,同时按照任意精度贴近各阶导数。所以,在多神经网络的3层前向结构中,输入上述3种单独神经网络的预测值,并将实际值当作网络输出结果,实现网络训练。本文将多神经网络结构描述为图2。其中,隐含层的选取采用经验公式2n+1的计算方式。

图2 组合预测的神经网络结构图

图2中,采用遗传算法设置初始化权值和阈值,使其赋值范围保持在[-1,1]之间。采用预测值和实际值,随机选取一组训练模式实现网络训练,得到多神经预测网络的实际输出结果。

其中,隐含层输出计算式为

Ly=ψp(∑E-F)

(10)

式中,L表示输出值,y表示隐藏层节点,ψ表示作用函数,E表示初始化权值,F表示初始化阈值,p表示训练次数。

(11)

随后,按照以下公式修正权值:

E(Z+1)=E(Z)+γ(Z)+ϑ(E(Z)-E(Z-1))

(12)

式中,Z表示循环次数,γ表示时变学习率,ϑ表示变动因子。通过上述计算完成权值修正,确保输出层误差达到预测要求,输出符合综合能源系统工作要求的负荷预测结果[11]。

1.4 完成预测模型参数校正

为了提升用户侧冷热负荷计算结果的准确性,本文按照调研和规范明确输入参数,并采用模拟软件实现预测模型参数校正,完成负荷预测模型的建立。

根据图3可知,预测模型建立过程中,模型参数校正是不可忽略的重要环节之一。在用户侧冷热负荷预测过程中,还应包含部分不确定性因素,避免负荷预测结果出现误差。本文以建筑负荷强度为核心,提出以Design Builder模拟软件为核心的参数校准策略。Design Builder模拟软件的应用,使得冷热负荷计算中通入动态负荷原理,利用有限差分法,结合反应系数法获取更准确地用户侧冷热负荷预测结果[12-13]。

图3 预测模型建立

本文利用Design Builder模拟软件输出模拟负荷数据,与当前负荷统计值进行对比,明确预测参数的误差。预先设计一个阈值,当预测误差高于设定阈值后,计算机收到即时反馈信息,对模型的输入参数进行调整,再进行重复模拟计算,直到预测模型输出结果的误差值稳定保持在允许范围内,将当前参数作为校正参数,完成综合能源系统的用户侧冷热负荷预测模型修正。

2 算例分析

为了验证本文设计负荷预测模型的应用性能,选择某一夏热冬冷地区采集相关数据,展开负荷预测算例分析。针对用户侧冷热负荷的主要计算参数,使用多神经网络预测模型获取该区域用户侧建筑负荷预测结果,将预测结果与实测值进行对比,采用误差评价指标判断本文设计模型的有效性。

2.1 选取算例分析数据

以某一多功能建筑示范区为例,分析区域内综合能源系统的工作特点,采集算例分析样本数据。该区域内建筑总面积达到了20万m2,主要由住宅公寓、中小型办公楼、小型宾馆、小型商铺以及大型商场5种建筑物组成。应用本文设计模型,预测建筑区域内综合能源系统用户侧冷热负荷。本文以夏季典型日为例,预测该区域逐时冷热负荷。根据综合能源系统负荷数据库中的预测因子,结合示范区内的建筑类型深入分析,得到夏季典型日逐时负荷先验信息如表1所示。按照时刻获取先验信息正态分布的平均值,考虑到标准差将假定标准差设置为14 W/m2。

表1 夏季典型日逐时负荷先验信息 单位:W/m2

通过对多功能建筑示范区的实地调查,以及综合能源系统监管平台,在示范区内随机选取3块面积相仿的区域,采集区域内的综合能源系统输入特征数据和系统历史负荷数据,汇总形成算例分析数据集。算例分析数据中数据量共有14万左右,考虑到算例分析数据的属性存在差异,对算例分析数据进行归一化处理,处理公式为

(13)

式中,x表示待处理数据,x′表示归一化处理数据,xmin、xmax表示原始数据的2个极值。数据归一化处理完成后,采用数字1～7表示日期类型数据中周一至周日,应用数字1～4将季节数据划分为春夏秋冬四个类型。将算例分析数据集划分为训练集和测试集,作用于下一步多神经网络训练。

在弓箭的压制下，土狼群开始出现了骚动和不安。或许它们认出了那是猎人的箭矢，它们开始胆怯、开始动摇，同时也更加地愤怒。

2.2 网络超参数设置

因为实验方法均使用了神经网络迭代训练和学习,获得预测最优值,为了提升模型预测结果的准确性,即提高神经网络的学习速度和训练准确率,需要针对多神经网络的超参数进行设置。超参数是网络初始化的值,给学习机选择一组最优超参数能够提高神经网络训练的准确率和速度,以尽快收敛到全局最优值,从而提高基于神经网络模型的预测方案精度。算例分析过程中,将全局初始学习率设置为0.01,以此为基础设置其他参数。针对综合能源系统用户侧冷热负荷数据的静态特征提取进行分析,提取通道中卷积层、池化层均为1层1维结构,前者结构内部卷积核数量为64,后者补偿值为30。除此之外,设置隐藏层神经元数量为150。用户侧冷热负荷预测的另一重要环节就是动态时序分析,算例分析过程中利用4层GRU隐藏层搭建分析通道,每个隐藏层的神经元个数逐层递增。最后,Maxout层和隐藏层组成输出模块,二者内部神经元数量分别为100个和1个。通过上述网络超参数设置,构建预测精度较高的模型,获取综合能源系统用户侧冷热负荷预测结果。

2.3 负荷预测结果分析

利用网络超参数设置完成后的模型结合表1的先验信息,获取多功能建筑示范区的综合能源系统用户侧冷热负荷预测结果。为了客观了解负荷预测结果的准确性,借助监管平台统计冷热负荷实测值,对比预测值与实测值形成图4所示的对比图。

图4 夏季典型日预测结果对比图

根据图4可知,本文设计预测模型得到的用户侧冷热负荷预测结果与实测负荷走向大致相同。整体来看,1～7时综合能源系统内主要负荷是宾馆酒店、居住类建筑,使得用户侧冷热负荷较低。从8时开始负荷不断增长,直到16时到达最高冷热负荷值。之后,用户侧冷热负荷逐渐降低,直到24时降到最低负荷。预测值与实测值较为接近,但是在各个时刻依旧存在不同程度的差额。

2.4 模型性能对比

为了加强算例分析结果的对比性,选用基于多层聚类、基于IPSO-WNN和基于神经网络的预测模型,应用同样的算例分析数据获取综合能源系统用户侧冷热负荷预测结果。本文通过预测值与实测值的逐时负荷相对误差,对比不同预测方法的相对误差,判断预测模型的应用性能。其中,逐时负荷相对误差作为一个性能判断指标,将实测点与预测点之间的差距直观呈现出来,计算式表示为

(14)

式中,δ表示逐时相对误差,当误差计算结果出现负数表明预测值相比实测值更小,Q表示预测逐时区域总负荷,Q1表示实测逐时区域总负荷。通过散点图表示4个预测模型的逐时相对误差,形成图5所示的对比图。

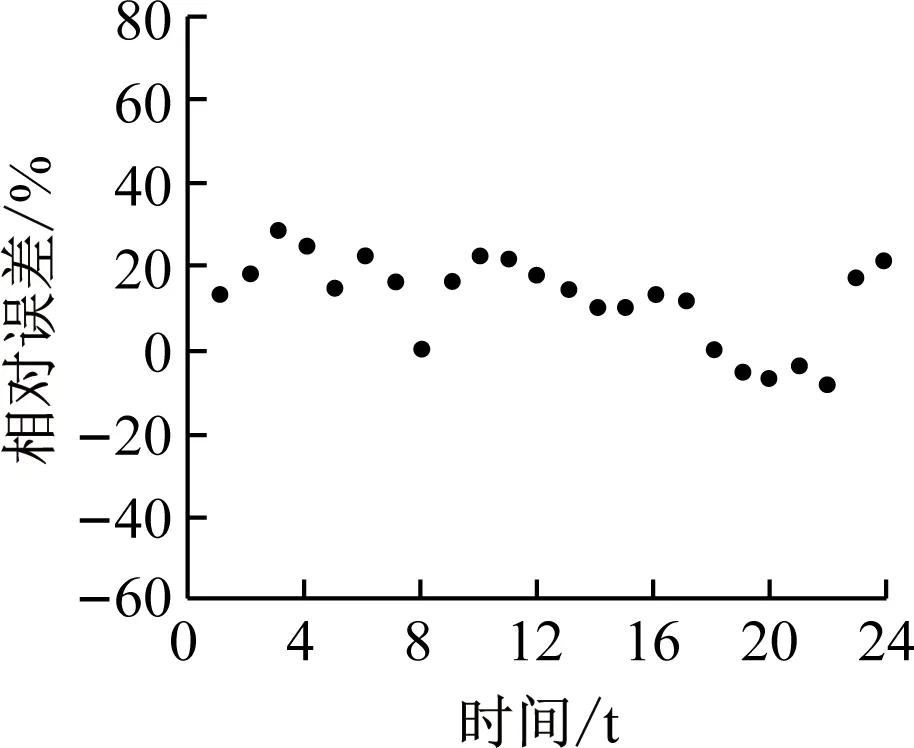
(a) 本文设计预测模型

根据图5可知,本文设计预测模型的逐时相对误差最大仅为29%,平均逐时相对误差为16%。而基于多层聚类的预测模型、基于IPSO-WNN的预测模型和基于神经网络的预测模型的平均逐时相对误差分别为31%、43%、55%。综上所述,本文设计预测模型的预测相对误差比其他预测模型低了15%、27%与39%,大大提升了模型预测精度。这是因为本文分析了用户侧冷热负荷影响因素,提取负荷计算的主要参数,结合BP网络、RBF网络和小波神经网络,优化多神经网络预测方法,并进行参数修正,保证了预测结果的高精度。

3 总结

以综合能源系统为核心,针对用户侧冷热负荷进行预测,有利于制定合理的能源供给策略。为了获取高精度的用户侧冷热负荷预测结果,结合BP网络、RBF网络和小波神经网络,生成多神经元网络结构,设计冷热负荷预测方法,使其具有较强的可行性和有效性,大大提升了预测精度,使预测用户侧冷热负荷更贴近实际负荷。

本文设计的预测模型主要以用户侧为重点进行讨论,尚未考虑概率预测模式,未来可以将该模式融入预测模型内,为综合能源系统的运行规划提供数据支撑。