风电机组双向支撑能力分析与自适应惯量控制策略
胡正阳 高丙团 张 磊 王文倬 潘沈恺
风电机组双向支撑能力分析与自适应惯量控制策略
胡正阳1高丙团1张 磊2王文倬3潘沈恺1
(1. 东南大学电气工程学院 南京 210096 2. 可再生能源并网全国重点实验室(中国电力科学研究院有限公司) 南京 210003 3. 国家电网有限公司西北分部 西安 710048)
针对高比例新能源电力系统暂态频率支撑需求,提出一种考虑双向支撑能力的风电机组自适应惯量控制策略。首先,基于典型风电并网模型,分析了不同渗透率、控制参数和扰动下系统的频率动态响应特性。其次,结合风电出力与转速关系曲线,给出风电机组对频率上升/下跌事件的双向惯量支撑能力定量分析方法。再次,提出风电机组自适应惯量控制策略,给出各参数的设计方法并基于状态空间方程分析了控制系统的小扰动稳定性。最后,基于RT-LAB搭建了实时仿真算例验证所提方法的可行性和有效性。仿真结果表明,所提控制策略能够保证风电机组根据自身能力和系统需求提供有效的惯量支撑,与已有典型控制策略相比,改善了低风速与高风速场景下的频率响应特性。
风电机组 惯量支撑 频率特性 自适应控制 小信号分析
0 引言
“十四五”是我国实现碳达峰的关键期和推进碳中和的起步期。近年来,风力发电作为清洁能源发电技术得到了广泛重视与发展[1-3]。风电的大规模并网以及传统火电机组的占比降低,导致系统等效惯量降低、一次调频能力削弱等问题[4-6]。同步机组中调速器、高压缸等其他机械部件的响应延时造成一次调频响应速度较慢,若系统的等效惯量较低,系统频率在扰动初始时刻会出现较大的变化率,在一次调频响应结束前可能发生较大偏移。惯量响应是暂态频率快速支撑的控制手段之一,在国家最新发布的风电场并网技术规定中也要求风电场具备惯量响应能力[7]。
目前通常采用虚拟惯量控制使风电机组具备惯量支撑能力[8-9],但固定系数的惯量控制参数整定困难且在不同扰动、电网不同工况下无法作出有效调整。若惯量系数较小,则风电机组无法提供有效的惯量支撑;若惯量系数较大,则风电机组所存储的有限动能在系统发生扰动后释放过快,导致风电机组转子转速过度跌落的问题[10]。为了克服传统策略固定增益系数的问题,有学者提出了变系数惯量控制策略,基于各风电机组状态(转速/风速)[11-13]或基于系统状态(频率/频率变化率)[5,14-19]来调整风电场的惯量响应控制参数。
基于风电机组状态的变系数惯量控制策略研究能够根据风电机组的频率支撑能力调节控制参数。文献[11]基于当前风机运行状态,使用正比于风电机组可释放动能的惯性增益,使风机在保证稳定运行的前提下可以在频率事件发生初期提供较大惯量支撑功率。文献[12]根据风速不同对虚拟惯量系数进行整定,在额定风速以下时惯量系数随风速升高而增大。文献[13]将惯量系数设计为随频率事件发生时间的推移而减小的抛物线函数,在频率事件发生的初始阶段惯性增益最大。但是,此类研究仅考虑了机组自身的支撑能力,而未深入考虑电力系统调频需求。
频率是风电场能获得的为数不多的电力系统状态量,而频率变化率能有效反映频率事件的严重程度以及当前系统的惯性强弱,在设计自适应惯量控制系数时应考虑系统的支撑需求。文献[14]较早地提出基于分段控制的风电有功功率-频率控制,通过频率分段使风电机组运行在不同的有功控制区间,改善了系统频率特性。文献[15]设计了随频率偏差值和频率偏差变化率变化的自适应惯量、一次调频系数,但其利用超级电容为系统提供调频功率支撑,对现有风电机组的改造要求较高。文献[16]将一次调频与惯量支撑功能组合,下垂系数设为随频率变化率升高而增大的参数,使得风电机组在扰动开始时提供较大功率支撑,在频率跌落速度变缓后提供较小功率支撑。在此基础上,文献[10]考虑了风机工作状态,将下垂系数设为同时随频率变化率和风机转速变化的参数,有效地提高了频率跌落最低值并改善风机转速过度跌落的问题,但其缺乏参数设计的理论支撑,且该文献中风机的稳态工作点为最大功率点跟踪(Maximum Power Point Tracking, MPPT),提供功率支撑会使风机运行在MPPT点左侧,从而危害系统的频率小扰动稳定性[20]。文献[19]设计了根据频率偏差自适应改变惯量系数的虚拟同步机控制策略,文献[5,17-18]利用模糊控制理论使惯量系数能同时根据频率偏差量和频率变化率而自适应变化。但虚拟惯量控制的目的是模拟同步发电机的惯性响应来抑制系统频率的快速变化,频率偏差应是一次调频控制关注的问题[10]。若频率偏差量大而惯量系数随之增大,系统受到小扰动时风电会提供强惯量支撑,从而导致转子转速过度跌落的问题。此外,模糊控制规则是凭经验设计的,论域的选择也缺乏理论支撑。
当前已有较多针对风电机组惯量响应的相关研究,但仍存在一些不足之处。首先,已有策略对于综合考虑风电机组自身支撑能力和电力系统惯量支撑需求的研究不够深入。其次,已有文献在评估风电机组转子存储的动能时,多以当前转速与转速下限之差作为基准,这使风电机组转速跌落至MPPT点左侧,危害了风电系统的小扰动稳定。再次,目前的研究多集中于解决频率下跌事件的惯量支撑,认为风电在系统有功功率过剩导致频率上升时具备足够吸收能量减载的能力,但实际上在低风速时,风电减载能力有限,应对频率上升事件的能力有限[21];高风速时风电机组到达额定转速,不具备继续提高转速存储动能从而降低输出功率的能力。虽然变桨法可以减载,但桨距角响应时间尺度过长,风电机组的变桨速率最大约为5°/s[22],不符合惯量支撑的需求。
因此,本文针对风电并网系统,提出了一种考虑双向支撑能力的风电机组自适应惯量控制策略,以期对并网风电机组的惯量支撑技术提供参考。首先,分析了电网的惯量支撑需求,并给出了风电机组双向惯量支撑能力的定量分析方法;进一步地,设计了风电机组自适应惯量控制器结构及参数,并基于小信号法分析了控制器的稳定性;最后,基于RT-LAB平台的仿真结果验证了本文理论分析的正确性,以及所提自适应惯量控制策略与传统控制策略相比在低风速与高风速场景下具有更佳的综合性能。
1 风电并网模型及惯性需求分析
目前并网风电机组以双馈风电机组和永磁直驱风电机组为主,由于风电机组的外特性相似,本文的惯量支撑能力分析思路及方法对两种机组均适用。永磁直驱风电机组依靠机组结构、故障穿越等方面的优势,逐渐成为主流机型,因此本文以永磁直驱风电机组为例进行分析。
1.1 风电机组建模及运行方式分析
全功率永磁直驱风力发电机组的机械功率可表示为[23-24]
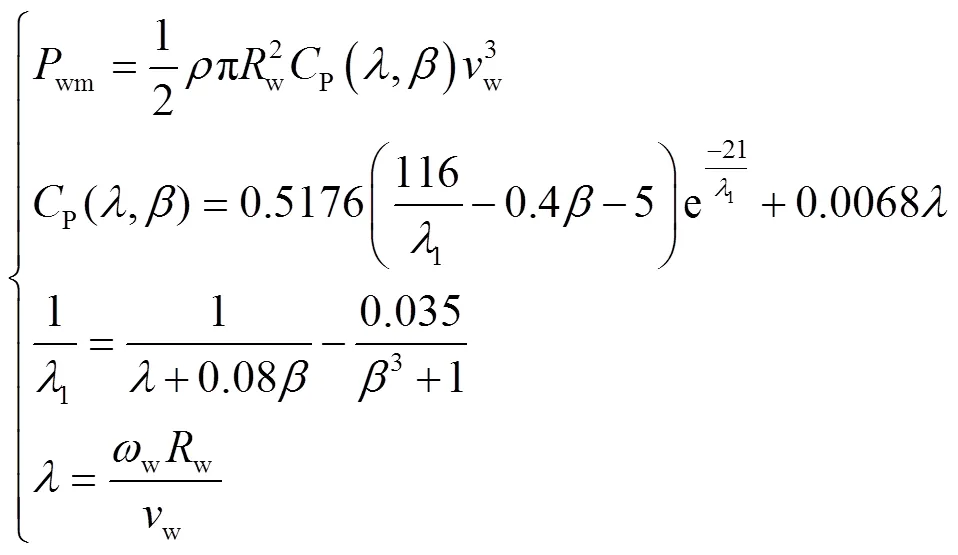
式中,wm为风电机组机械功率;为空气密度;w、P、w、w分别为风力机的叶片半径、风能利用系数、叶尖速比、桨距角、转速和入口风速。
在减载运行的情况下,风电机组的功率为
式中,wdel为风电机组减载后的给定功率;opt为风电机组的最大功率;%为风电机组减载率。由式(1)可得,当w小于最大转速时,最大功率跟踪曲线方程为
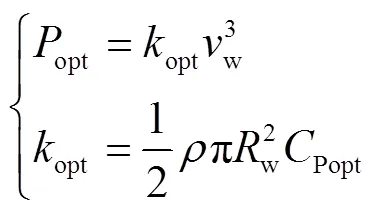
式中,opt为风电机组最大功率跟踪系数;Popt为最佳风能利用系数。将式(3)代入式(2),则减载运行曲线方程为
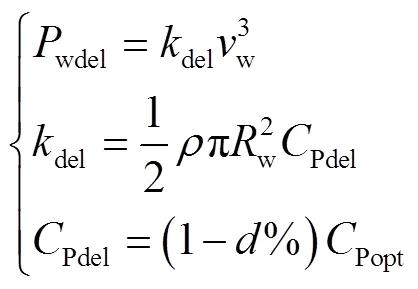
式中,del为减载功率跟踪系数;Pdel为减载风能利用系数。
1.2 电网惯性响应需求分析
为了分析风电并网的频率响应特性,将电力系统等效为一台同步发电机,风电场为单机等值模型。结合文献[18],风电并网系统的标幺化小信号模型如图1所示。需要注意的是,虽然本文主要研究风电的惯性响应,但等效电力系统中仍需考虑同步发电机的一次调频控制,否则系统的频率响应特性会发生变化,无法保证理论分析及算例的真实性。
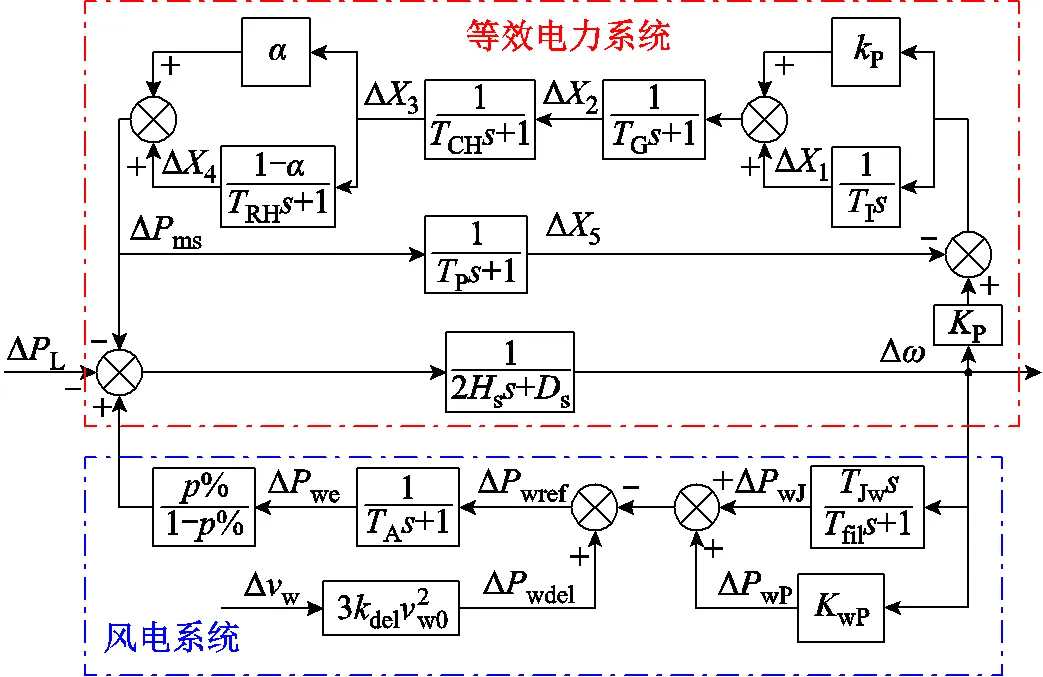
图1 风电并网系统小信号分析框图
图1中,等效电力系统的频率响应小信号模型如式(5)~式(11)所示。
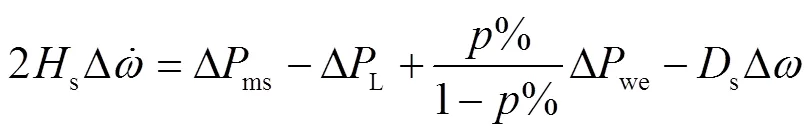
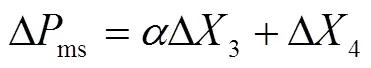
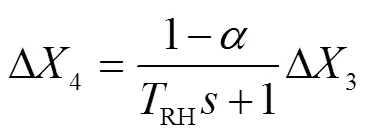
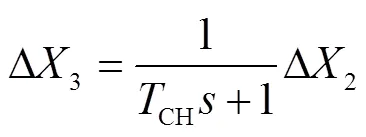
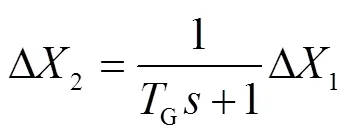
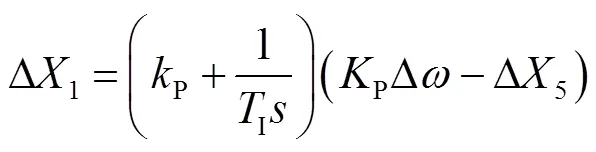
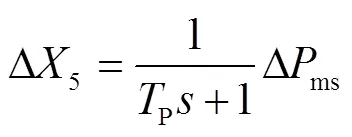
式中,为系统角频率;s为同步发电机惯性时间常数;s为同步发电机阻尼系数;ms为同步发电机机械功率;L为负荷电磁功率;%为风电渗透率,是风电装机容量与系统总容量之比;we为风电输出有功功率;P为火电机组一次调频系数;1~5分别为同步发电机调频模型的中间状态变量;P和I分别为PI环节的比例系数和积分时间常数;G为油动机时间常数;CH和RH分别为高压缸和中压缸容积时间常数;P为测功时间常数;为高压缸功率百分比。
由于风电系统与等效电力系统分别以风机容量和同步机容量作为各自标幺化的基准,因此整个并网系统的分析中需要利用风电渗透率%来进行标幺值换算。在小信号模型式(5)中,通过%/(1-%)将以自身容量为基准的风电有功功率输出转换为以同步机容量为基准的标幺值形式,保证了以同步机摇摆方程为依据的频率计算的准确性。
由式(5)可知,系统受到负荷扰动的最初时刻,由于同步发电机机械功率、转速与风电输出功率尚未变化,同步发电机转速变化率与扰动大小成正比,即系统频率变化率与扰动大小成正比。
当风电参与惯性响应与一次调频时,其功率平衡关系式为
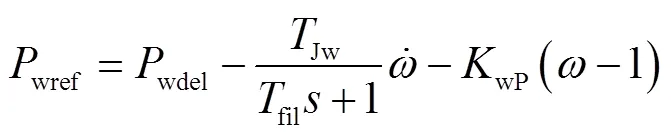
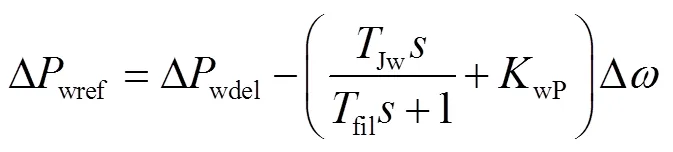
当风电机组减载运行时,对式(4)进行小信号分析可得
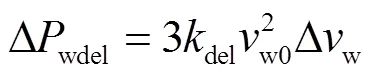
式中,下标带0的变量为小信号分析的稳态值。由于风电系统的电磁暂态过程远快于其机电暂态过程,因此可忽略机组和变流器的电磁调节过程,将其等效为一个惯性环节[25-26],且惯性时间常数A较小,一般为0.2 s[27]。风电系统的电磁暂态调节过程为
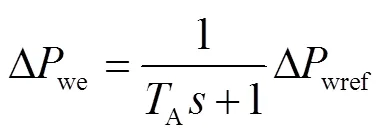
风电机组的转子运动方程为
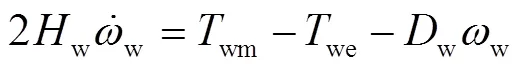
式中,w为风电机组惯性时间常数;wm为风电机组的机械力矩;we为风电机组的电磁力矩;w为风电机组的轴系阻尼系数。
对式(16)进行线性化处理得
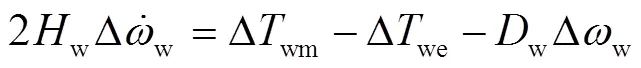
在不同风电渗透率及惯量控制系数条件下,频率变化率均可以有效地反映系统所受扰动强弱,风电机组的虚拟惯量系数需要根据系统频率变化率的大小进行自适应调节[5],从而具备符合电网需求的惯量支撑控制技术。
2 风电机组双向惯量支撑能力分析
当前研究中,为了保证风电场的总发电量,通常让风电机组运行在MPPT模式,在频率事件发生后控制短暂地偏离最佳运行点,并在一定时间后退出调频返回稳态工作点。然而,由于MPPT控制下的风电场有功出力由当前风速决定,具有明显的随机性与间歇性特征。电力系统频率控制的本质目标是维持电力电量的供需平衡[28],而风电有功功率波动妨碍系统达到该控制目标,从而对频率稳定性造成影响。目前,通过减载跟踪调度指令的方式来满足系统的调度需求是一条可行的技术路线[29-31]。在国标GB/T 19963.1—2021《风电场接入电力系统技术规定第1部分:陆上风电》中规定的限值模式与差值模式均要求风电场采用减载控制。同时,若风电机组从最大功率点继续减小转速来提供有功支撑,在退出调频后会造成系统频率二次跌落[32],且风机在风速变化时存在失稳的风险[33]。因此,本文设定风电机组在稳态时通过减载跟踪调度指令,并依据风机在超速后所存储的动能大小来分析风电机组自身的惯量支撑能力。
2.1 频率下跌的惯量支撑
系统频率下跌时,需要电源侧增加有功功率来提供惯量支撑。风电机组运行在超速减载状态,其可用来支撑惯性的能量为超速运行所存储的多余动能。风电机组的转速变化范围一般为0.7(pu)~1.2(pu)[34-35],因此本文取风电机组安全运行转速下限为0.7(pu),上限为1.2(pu)。当风速较大时,风电机组转速到达上限,则无法继续使用超速法进行减载,因此超速法适用的范围为中低风速区。在减载率的取值确定的情况下,可以将风速从小到大分为三个区间:区间d1[dmin,d1)、区间d2[d1,d2)和区间d3[d2,wn]。其中,dmin为风电机组减载转速达到转速下限对应的风速,减载转速即为风电机组减载%运行时对应的转速;d1为风电机组最佳转速达到转速下限对应的风速,最佳转速即为风电机组在MPPT点对应的转速;d2为风电机组减载转速达到转速上限对应的风速;wn为额定风速。风速若在区间d1、d2内,风电机组仅使用超速控制进行减速;风速若在区间d3内,风电机组使用超速和变桨控制减载。若减载率一定,则根据式(4)可以得到Pdel,代入式(1)可以得到减载叶尖速比del,根据式(18)可以求得各风速对应值。
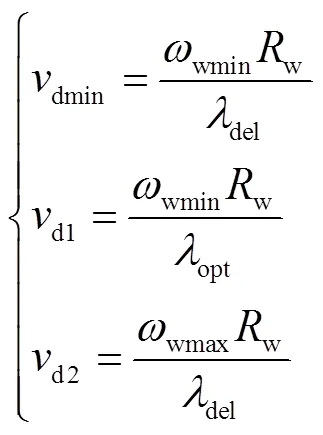
式中,wmin为风电机组转速下限,取0.7(pu);wmax为风电机组转速上限,取1.2(pu);opt为风电机组最佳叶尖速比。
为了更直观地展示不同风速下风电机组出力和风机转速的关系,给出了图2所示的关系曲线。图2中各风速值与式(18)和式(21)所得风速区间对应,橙色虚线对应频率下降、蓝色点画线对应频率上升。另三条曲线分别为风电机组不同风速下MPPT点、减载%运行点、减载2%运行点的连线。若风速恰好为dmin,则风电机组运行在A点,减载运行转速del刚好达到转速下限,此时所能提供的动能仍为0。若风速在区间d1[dmin,d1)中,风机运行点由A点向B点移动,其减载转速高于转速下限,但最佳转速仍低于转速下限,此时风电机组的转速调节范围为转速下限wmin至减载转速del。当风速达到d1,风电机组运行于B点,其最佳转速等于转速下限,此时为了避免频率的二次跌落,风电机组转速最低调至最佳转速。风速到达区间d2[d1,d2)后,风机运行点由B点向C点移动,最佳转速高于转速下限,此时风电机组的调速范围为最佳转速opt至减载转速del。若风速为d2,风电机组运行于C点,减载转速达到了转速上限,风速继续增大至区间d3[d2,wn]中,为保证运行安全转速无法增加,仅利用超速法无法满足减载要求,需要使用变桨法配合超速法减载。由于风机调整桨距角会造成机械磨损,且速度较慢一般为5°/s,因此变桨法减载不能提供惯量支撑所需能量,此时机组转速调节范围为最佳转速opt至转速上限wmax。当风速到达风电机组额定风速时,风机运行在最大转速处恰好为MPPT模式,无法使用超速法继续减载。
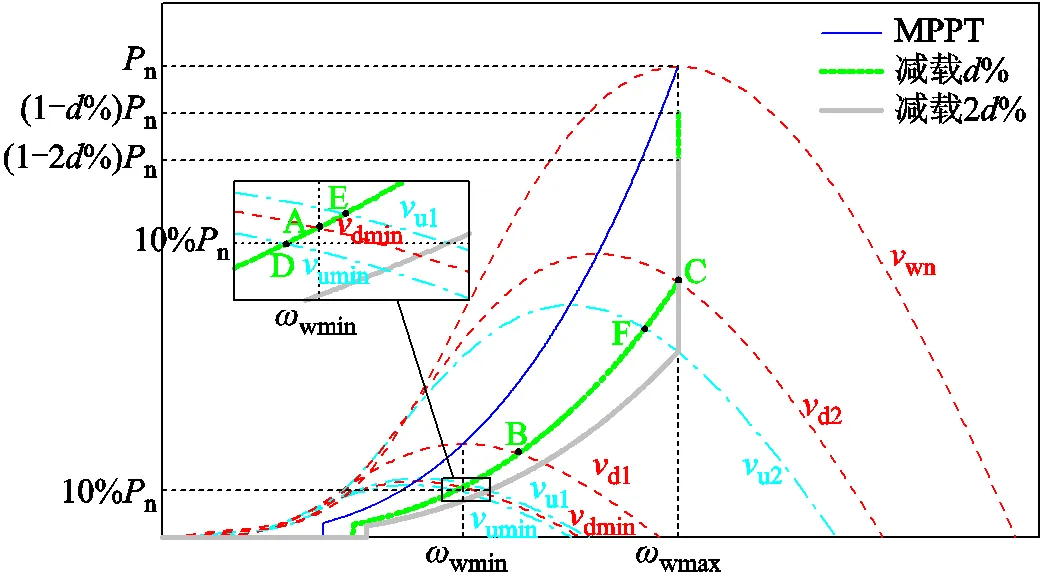
图2 不同风速下风电机组出力和风机转速关系曲线
根据以上分析,当风速在三个区间范围内时,风电机组可释放的动能分别为
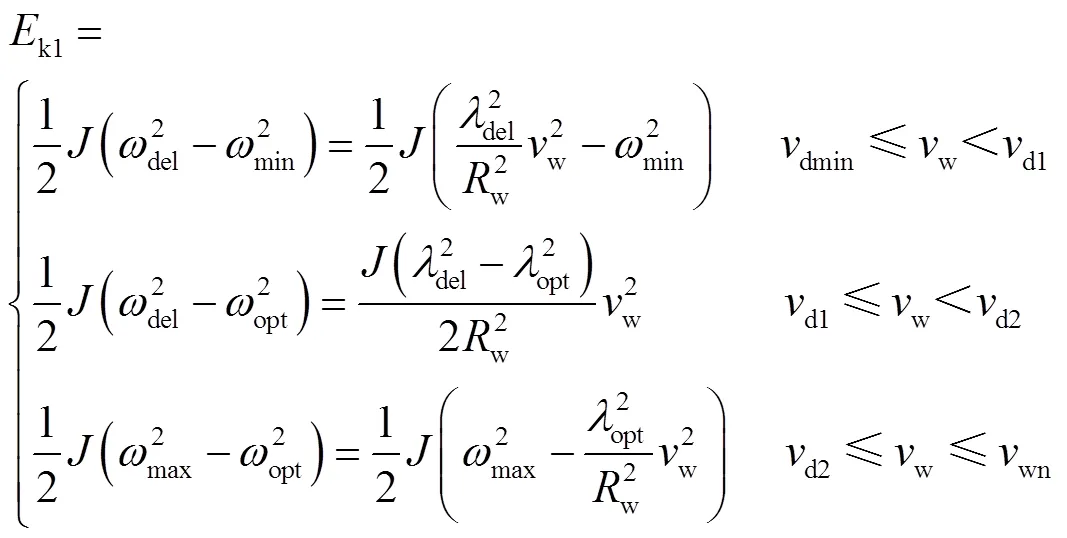
式中,k1为风电机组可释放的动能;为风电机组转子的转动惯量。根据式(19)可知,在各区间内,机组可释放的动能均为风速的二次函数。
2.2 频率上升的惯量支撑
当系统频率上升时,需要源侧减少有功功率来提供惯量支撑。风电机组运行在超速减载状态,其可存储的惯量支撑能量为当前最大转速到当前转速的动能差。根据中华人民共和国电力行业标准DL/T1870—2018《电力系统网源协调技术规范》的有关规定,新能源参与调频时有功出力降至额定出力的10%即可不再向下调节。此外,新能源向上与向下调节出力幅度一般相同,因此本文中设定风电机组在减载%条件下可继续向下调节%的当前最大功率,且最低出力为10%额定功率。此时,可知最大叶尖速比up与减载2%的叶尖速比相同。定义风电机组减载%运行对应的转速为减载转速,减载2%运行对应的转速和叶尖速比为最大调节转速adj和最大调节叶尖速比adj。
由式(4)可同理得减载2%运行曲线方程为

将风速从小到大分成三个区间,区间u1[umin,u1)、区间u2[u1,u2)和区间u3[u2,d2]。其中,umin是风电机组减载%运行达到10%额定功率n对应的风速;u1是风电机组减载2%运行达到10%额定功率对应的风速;u2是风电机组最大调节转速达到额定转速时对应的风速。根据式(21)可以求得各区间的边界风速值。

如图2所示,若风速恰好为umin,则风电机组运行在D点,减载运行功率为10%n,由于吸收动能需要减少出力,而规定的风电机组参与调频最低出力为10%n,因此此时所能吸收的动能仍为0。若风速在区间u1[umin,u1)中,风机运行点由D点向E点移动,风机的减载运行功率超过10%n,但减载2%的功率未超过10%n,此时风电机组转速调节范围有限,为减载转速del至10%n对应的转速up。当风速达到u1,风电机组运行在E点,减载2%后刚好为10%n,为了避免过度调节导致的脱机风险,同时保持机组出力向上、向下调节范围的一致性,转速最高调节至最大调节转速adj。风速达到区间u2[u1,u2)后,风机运行点由E点向F点移动,减载2%出力仍高于出力下限10%n,此时风电机组的调速范围为减载转速del至最大调节转速adj。若风速为u2,风电机组运行在F点,则最大调节转速adj达到转速上限,风速继续增大至区间u3[u2,d2]中,由于安全转速限制,机组转速的调节范围变为减载转速del至转速上限wmax。当风速达到d2后,风电机组运行于C点,减载转速也达到转速上限,无法继续增加转速存储动能,也不再具备频率上升的惯量支撑能力。
因此,当风速在三个区间范围内时,风电机组可吸收的动能分别为
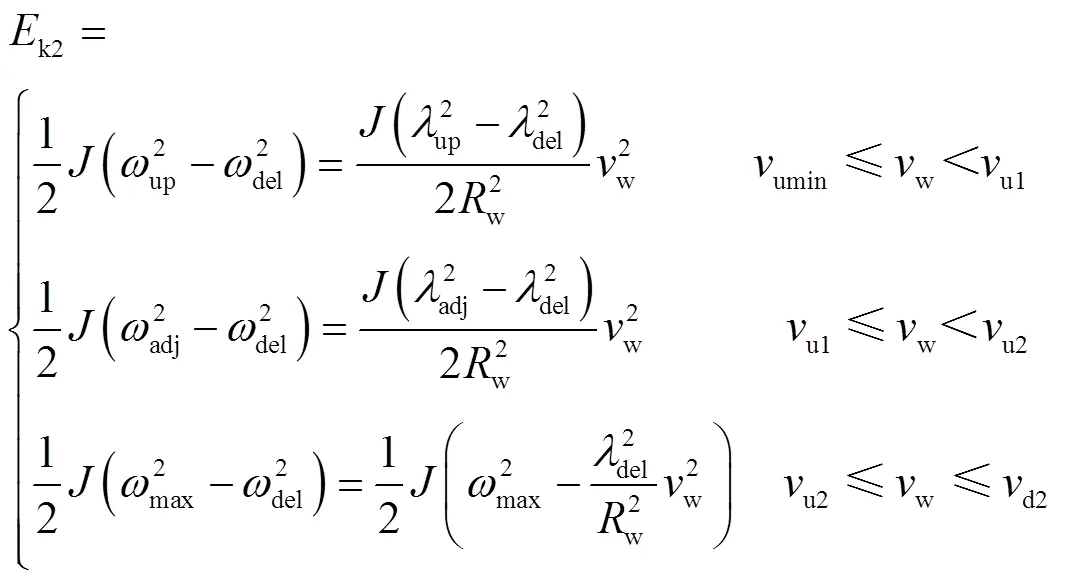
式中,k2为风电机组可吸收的动能;up、up分别为风电机组减载至10%额定功率时对应的转速和叶尖速比;adj的计算方法同del。up随风速的改变而变化,具体数值可以通过查表法获得。根据式(22)可知,在各区间内,机组可吸收的动能均为风速的二次函数。
基于以上对于不同风速区间的风电机组动能裕度定量计算,综合给出风电机组为应对频率事件进行双向惯量支撑所能释放/吸收的动能与风速的关系,如图3所示。
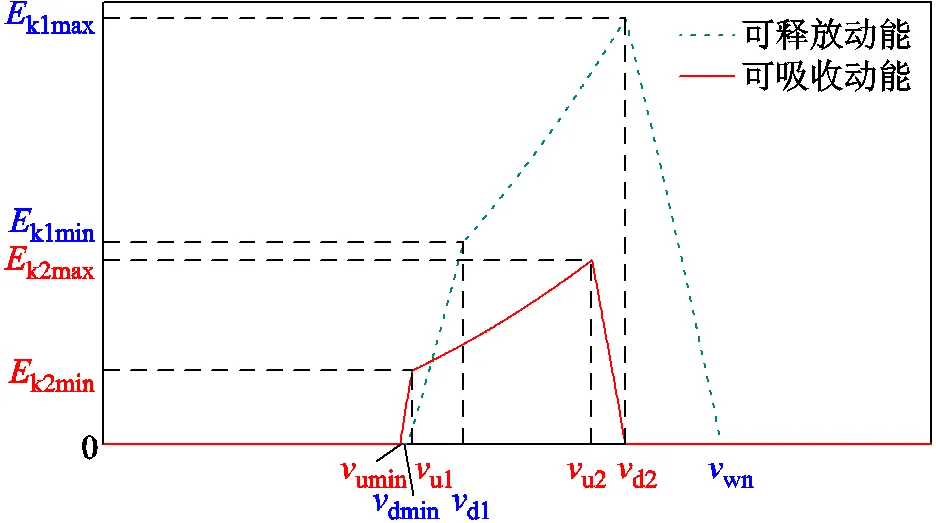
图3 不同风速下风电机组可释放/吸收的动能曲线
从图3中(蓝色)点线可以看出,风电机组可释放的动能在风速低于dmin时为0,因为此时机组在减载运行状态下转速未达到0.7(pu)。风速在dmin与d2之间时,机组可释放的动能随风速增大而增大,而风速超过d2后,机组可释放动能随风速增加而减小,直至达到额定风速wn,为避免系统频率二次跌落,频率下跌时机组不再提供惯量支撑。
从图3中(红色)实线可以看出,风电机组可吸收的动能在风速低于umin时为0,因为此时机组在减载运行状态下出力未达到最低安全出力0.1(pu),无法继续减载存储动能而参与频率上升的惯性响应。风速在umin与u2之间时,风机可吸收的动能随风速增大而增大,而风速超过u2后,机组可吸收的动能随风速增加而减小,直至达到d2,此时机组减载转速达到最大转速,无法继续吸收动能,从而不具备频率上升的惯量支撑能力。
对比图3中两条曲线可知,在大多数情况下风电机组动能的释放能力比吸收能力更强,意味着风电机组对频率下降事件的惯量支撑能力比应对频率上升事件更强,这建立在本文规定风电机组向上与向下调节的功率裕度相同的条件下。由图2中风电出力与转速的关系可知,风电机组在远离MPPT后曲线斜率随w增大而增大,说明相同功率变化量对应的转速调节幅度逐渐减小,而转速调节幅度变小又导致了能存储的动能减小。
值得注意的是,图3所得结论基于设定的减载率及调频出力区间。若实际参数与本文所设不同,只需修改参数进行计算,分析方法无需修改。
3 风电自适应惯量控制策略
基于系统的惯量支撑需求分析和风电的惯量支撑能力评估,本文提出了一种风电自适应惯量控制策略,自适应控制器根据d/d、w和w对虚拟惯量系数进行自适应调整,风电自适应惯量控制框图如图4所示。
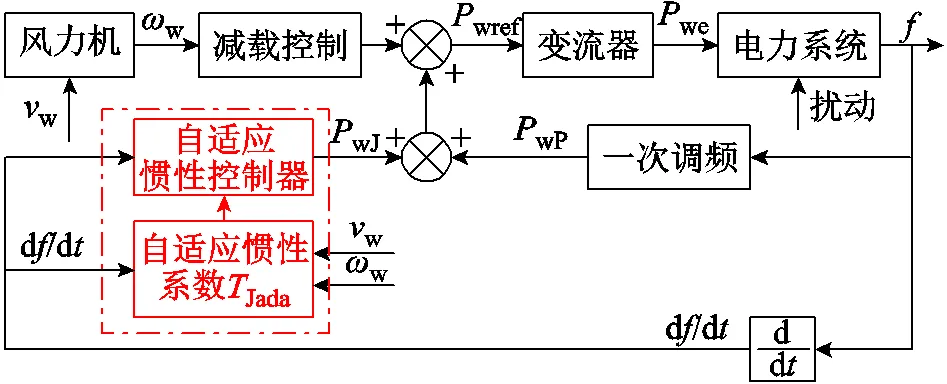
图4 风电自适应惯量控制框图
虚拟惯量控制设计的初衷就是为了模拟同步发电机的惯量响应,也就是在负荷功率变化时,能产生一个与频率变化率d/d负相关的补偿功率。利用自适应惯量系数Jada来模拟同步发电机运动方程中的惯性时间常数J,设置图4中自适应惯量控制数学模型为
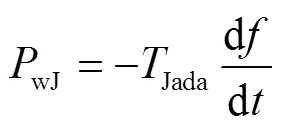
频率是风电场能检测到的系统变量,且频率变化率能有效反映系统当前扰动的强弱,因此需要以频率变化率d/d作为输入对惯量系数进行自适应调整。设计了一个具有上下限、左右对称和对d/d的灵敏度可调的自适应惯量系数Jada为
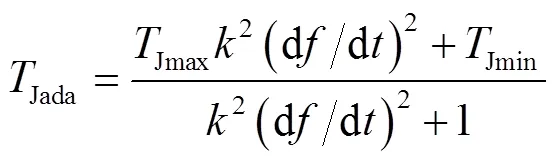
式中,为自适应因子;Jmax和Jmin分别为惯量系数的最大值和最小值。
3.1 自适应惯量控制参数设计
3.1.1 自适应因子
根据所设计的自适应惯量系数表达式(24),可得Jada与d/d的关系曲线如图5所示。
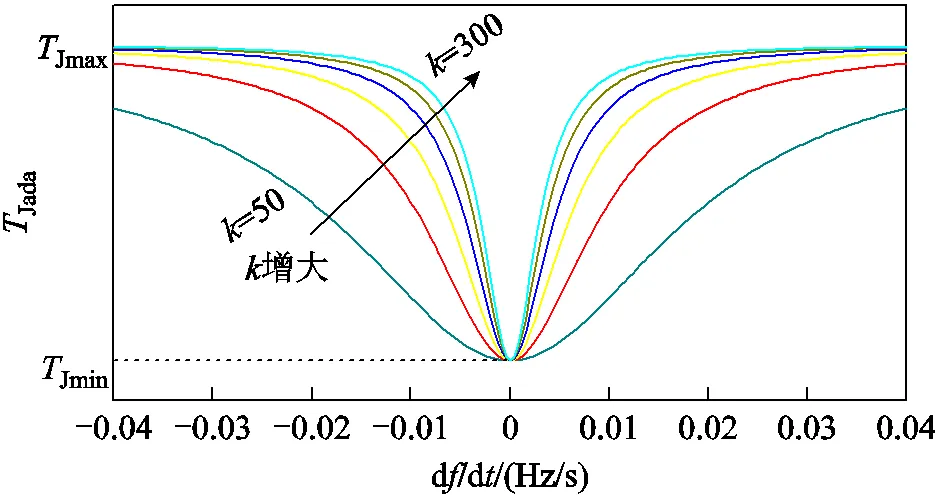
图5 TJada与df/dt的关系曲线
图5中,从50每次增加50直至300,共6条曲线。由图5可以看出,随着d/d绝对值的增加,Jada从Jmin开始逐渐增大,最后无限趋近于Jmax。越大,Jada在初始阶段的变化越明显并更快地趋于平稳。在d/d相同的情况下,越大,Jada越大。同时,考虑到Jada的频繁瞬变可能会造成风电机组疲劳载荷的积累,应对Jada变化率进行约束。
自适应因子的表达式为
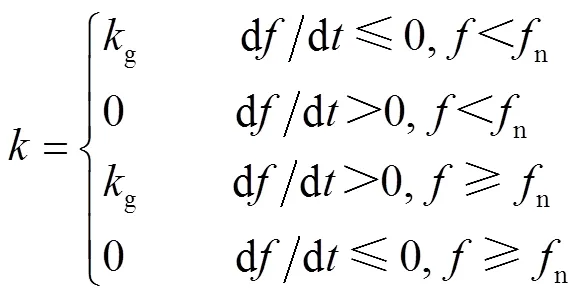
式中,g为常数。根据2015年锦苏直流故障的录波数据,故障后华东电网的频率变化率约为-0.08 Hz/s,频率跌落深度为0.41 Hz[36]。考虑到电力系统一般允许的频率波动范围为±0.2 Hz(约为锦苏直流故障频率跌落深度的一半),本文认为频率变化率超过±0.04 Hz/s时系统所受扰动即为剧烈扰动,风电机组需要提供强惯量支撑。基于图5对自适应因子与自适应惯量系数Jada的分析,参数g的取值应使频率变化率达到0.04 Hz/s时的Jada趋近于Jmax,则取50~100较为合适:高于100则Jada对d/d过于敏感;低于50则Jada在频率变化率达到0.04 Hz/s时仍无法提供较大支撑。
设计自适应因子的目的是确保当频率远离额定频率n时,新能源发电能提供系统需要的惯量支撑;当频率向额定频率方向变化时,惯量支撑对系统频率的恢复起反作用,此时新能源发电不提供惯量支撑,促进了频率的快速恢复。
3.1.2 惯量系数最大值Jmax与最小值Jmin
与一次调频和二次调频相比,惯量支撑的时间尺度最短,它一般针对波动频率较高、幅值较低的负荷。根据前文分析,频率变化率超过0.04 Hz/s时需要风电机组向系统提供其能力范围内最大的惯量支撑。电力系统频率跌落至最低点时间通常为5~10 s,本文要求风电机组在面对剧烈扰动时能以最大自适应惯量系数Jmax进行5 s的支撑。可以通过风电机组当前的转速和所需要支撑的功率来计算惯量系数的最大值Jmax。
首先,当自适应惯量系数取Jmax时,根据式(23)可以得到风电机组的惯量支撑功率。此时,可求出风电机组转子上的不平衡力矩为
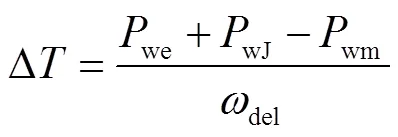
根据转子的合力矩和牛顿第二定律,可以求出风电机组转子的加速度为
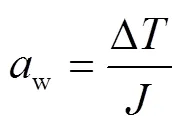
借助Newton-Raphson迭代法逐次逼近的思想,可以通过逐次逼近的方法来计算风电机组转子到达调节极限范围所用的时间,即
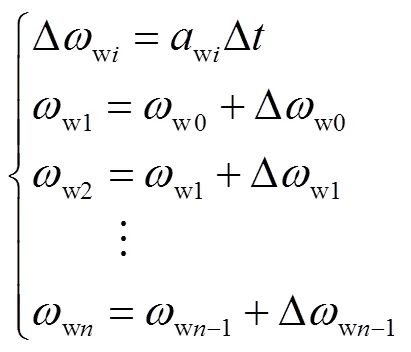
经过次迭代后,机组转速wn达到了调节边界,那么此时惯量支撑的最大时间即为Δ。设置一个较小的Jmax的初始值,令Δ=5 s,若wn未达到前文对风电机组双向惯量支撑能力分析中的调节边界,则增加Jmax后再进行一次迭代计算,如此循环,直至wn刚好达到支撑边界,认为此时风电机组在遭遇频率扰动后5 s通过调节转速释放/吸收动能刚好达到能力允许的极限,输出当前的Jmax作为本次的计算结果。
在调频过程中,由于需要改变转速来吸收/释放动能,风电机组工作点会不断偏离减载%的预设点,导致风电惯量支撑能力改变。由于实时进行迭代计算的计算量较大,会降低控制器的工程适用性。因此,仅计算额定频率工况下的惯量系数最大值,并通过当前风电吸收/释放动能能力与式(19)和式(22)中对应风速区间内减载预设点的动能吸收/释放能力之比对其进行修正,修正式为
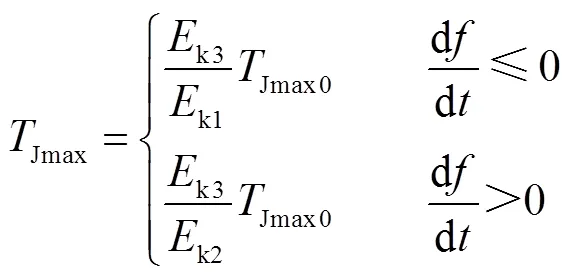
式中,Jmax0为迭代计算得到的惯量系数最大值;k3为当前风电可吸收/释放的动能,即
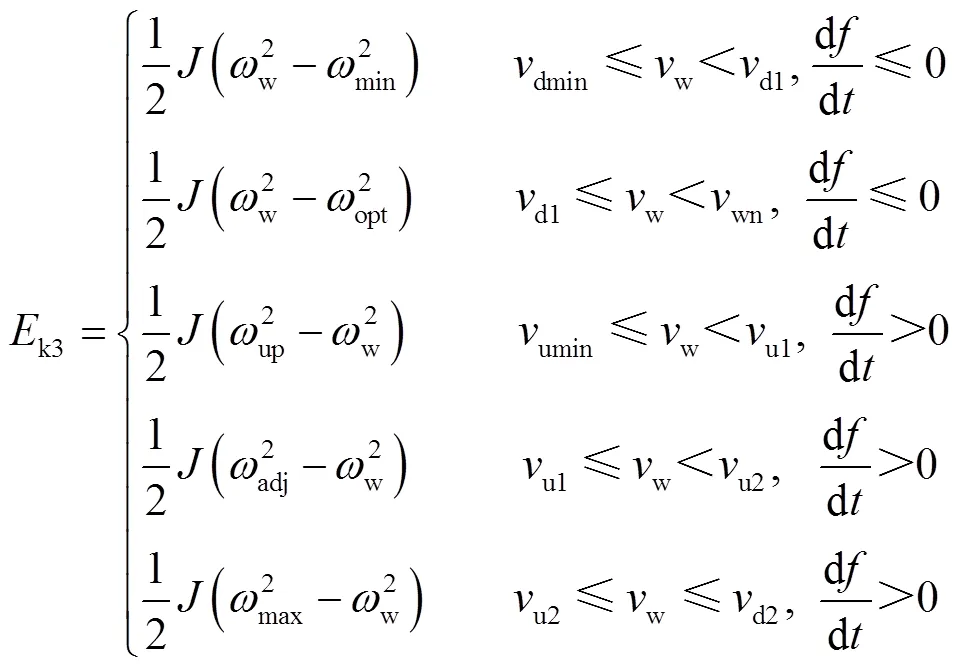
此时,所设计的Jmax保证了风电机组在遭受剧烈扰动时可以提供自身能力范围内并满足支撑时间要求的最大惯量支撑。
结合式(24)和式(25)可以看出,当频率向远离额定频率方向变化时,自适应惯量系数主要取决于Jmax,而当频率向靠近额定频率方向变化时,自适应惯量系数等于惯量系数最小值Jmin。为了保证所提策略满足国家标准[7]的要求,Jmin取为Jt。其中J取12 s,t为风电场有功功率。
3.2 控制器稳定性分析
将风电并网系统写为状态方程的形式,即
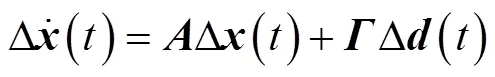
式中,Δ=[Δ1Δ2Δ3Δ4Δ5ΔΔwJΔwe]T为状态向量;Δ=[ΔLΔw]T为扰动量。系统矩阵和如附录式(A1)和式(A2)所示。
此时,线性系统的特征值可根据式(32)得出。
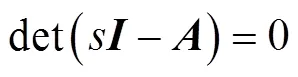
根据式(32)可画出系统随风电惯量系数变化的根轨迹(根轨迹绘制参数见第4节仿真分析),如图6所示,风电虚拟惯量系数从0增至500。
根据图6可以看出,主导极点均位于虚轴左侧,证明了系统的稳定性。系统主导极点随风电惯量系数增加而逐渐靠近虚轴,阻尼比减小。且随着风电惯量系数的增大,系统的根轨迹变化幅度逐渐减小。
4 算例分析
为了验证本文理论分析的正确性和所提自适应惯量控制策略的有效性,基于RT-LAB OP5700实时仿真平台搭建了风电场在母线9处并入3机9节点的标准系统[37],RT-LAB实时仿真平台如图7所示。

图7 RT-LAB实时仿真平台
仿真系统中的关键参数见表1,火电机组容量、线路等其他参数参考文献[18, 37]。4.1节~4.3节中风电装机容量为215 MW,风电渗透率为35%。基于双向惯量支撑能力的评估结果,umin=5.38 m/s,u1=5.6 m/s,u2=8.85 m/s,dmin=5.52 m/s,d1=6.53 m/s,d2=9.46 m/s,为便于文字描述并使读者更直观地感受风速大小,本文基于图3定义低风速区间为[umin,d1),中风速区间为[d1,d2),高风速区间为[d2,wn]。
表1 仿真系统关键参数

Tab.1 Parameter values of the simulation system
4.1 中风速小扰动场景
设置风电场风速为8 m/s,=5 s时负荷突增0.005 2(pu)的扰动(以总装机容量为标幺化基准值),风电场分别采用自适应惯量控制策略、文献[18]所提模糊自适应控制策略、大惯量系数控制策略和国标[7]中规定的惯量控制策略(后文简称标准策略),系统的频率、频率变化率(Rate of Change of Frequency, ROCOF)、风电有功功率、风机转速和风电惯量系数如图8所示,仿真结果见表2。表2中频率最低点为在本次扰动下频率跌落的最低值;跌落时间为扰动开始至频率跌落到最低值之间的时间。
当系统受到小负荷扰动时,由于频率变化较小,对惯量支撑的需求不高。从图8a及表2中可以看出,自适应惯量控制和模糊自适应控制的控制效果相似,介于标准策略和大惯量系数控制策略之间。由于负荷扰动较小,系统对惯量支撑的需求较低,频率无需提供强支撑而仍保持在正常范围内波动。
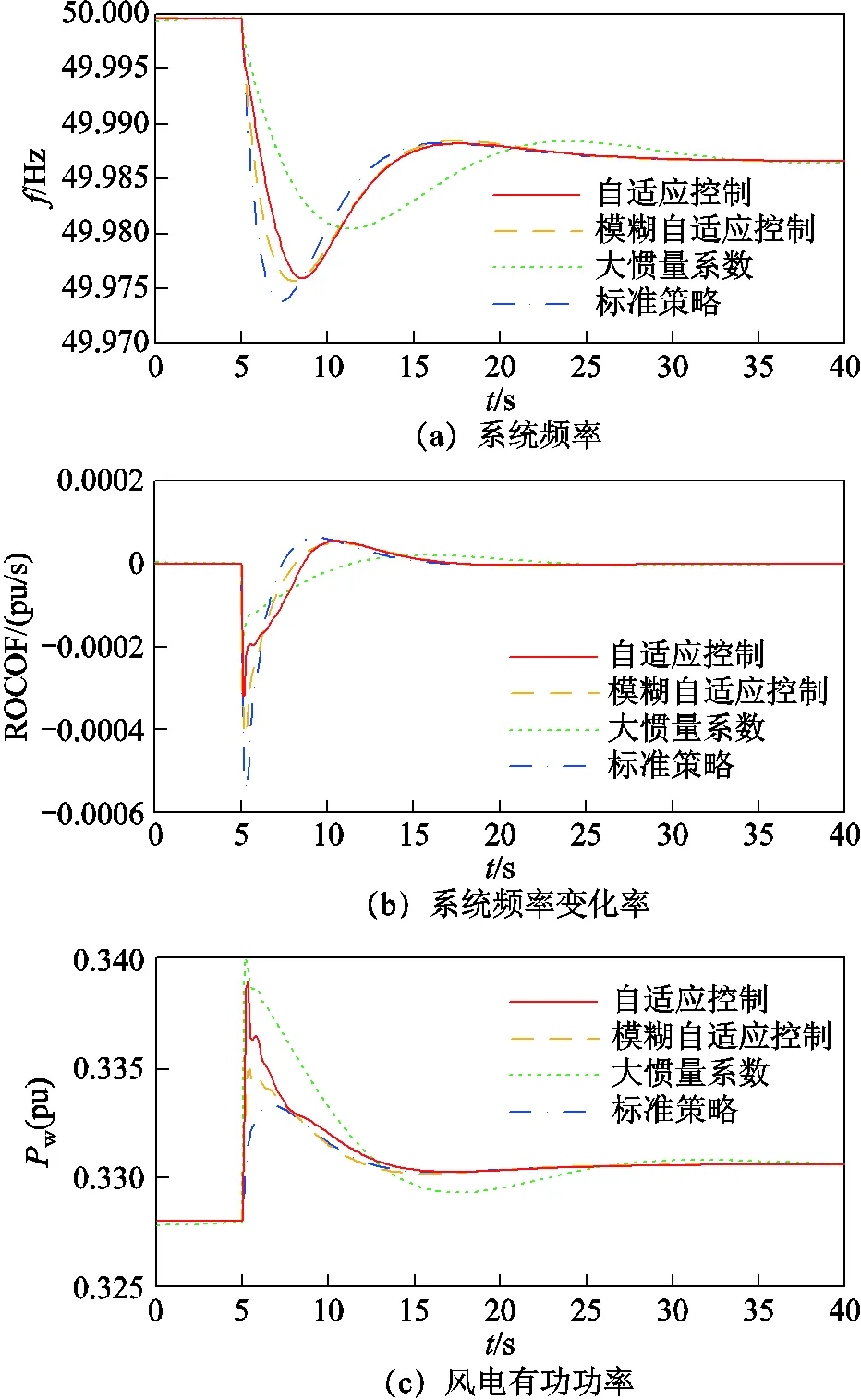
表2 中风速小扰动仿真结果

Tab.2 Simulation results with medium wind speed and small disturbance
4.2 低风速大扰动场景
设置风电场风速为6.5 m/s,=5 s时负荷突增0.035(pu)的扰动(以总装机容量为标幺化基准值),系统的频率、频率变化率、风电有功功率、风机转速和风电惯量系数如图9所示,仿真结果见表3。
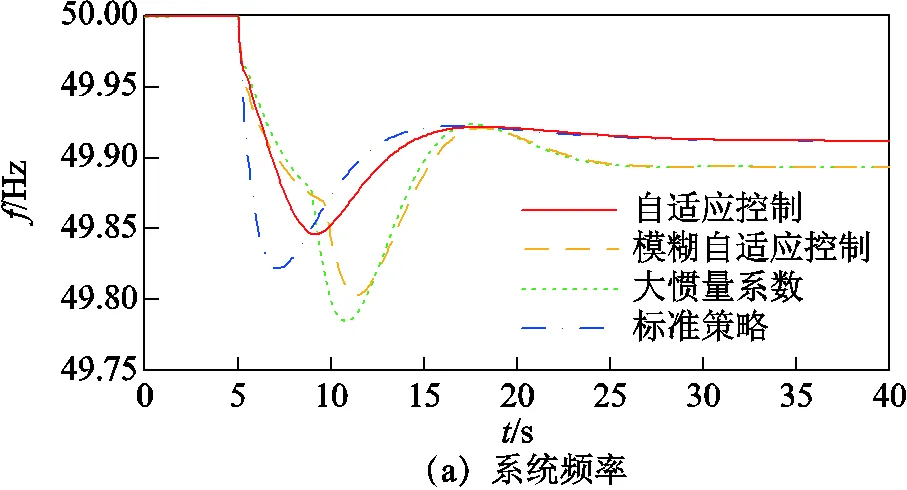
表3 低风速大扰动仿真结果

Tab.3 Simulation results with low wind speed and large disturbance
风电场在低风速状态下由于惯量支撑能力有限,在系统受到大扰动时无法提供足够的惯量支撑,若不根据惯量支撑能力评估结果相应地改变风电场控制策略,会导致风机转速过度跌落从而退出调频。从图9c、图9d中可以看出,大约在= 9s后采用模糊自适应控制和大惯量系数控制的风电场均由于到达转速最低限值而退出调频,无法应对后续频率事件,而采用自适应惯量控制和标准惯量控制策略的风电场未退出调频,因此在频率恢复至稳态后仍能参与系统一次调频。从图9a及表3中可以看出,自适应惯量控制的系统频率跌落最低值为49.846 Hz,明显优于其他三种控制策略。
4.3 高风速大扰动场景
设置风电场风速为9.5 m/s,=5 s时负荷突增0.035(pu)的扰动(以总装机容量为标幺化基准值),系统的频率、频率变化率、风电有功功率、风机转速和风电惯量系数如图10所示,仿真结果见表4。
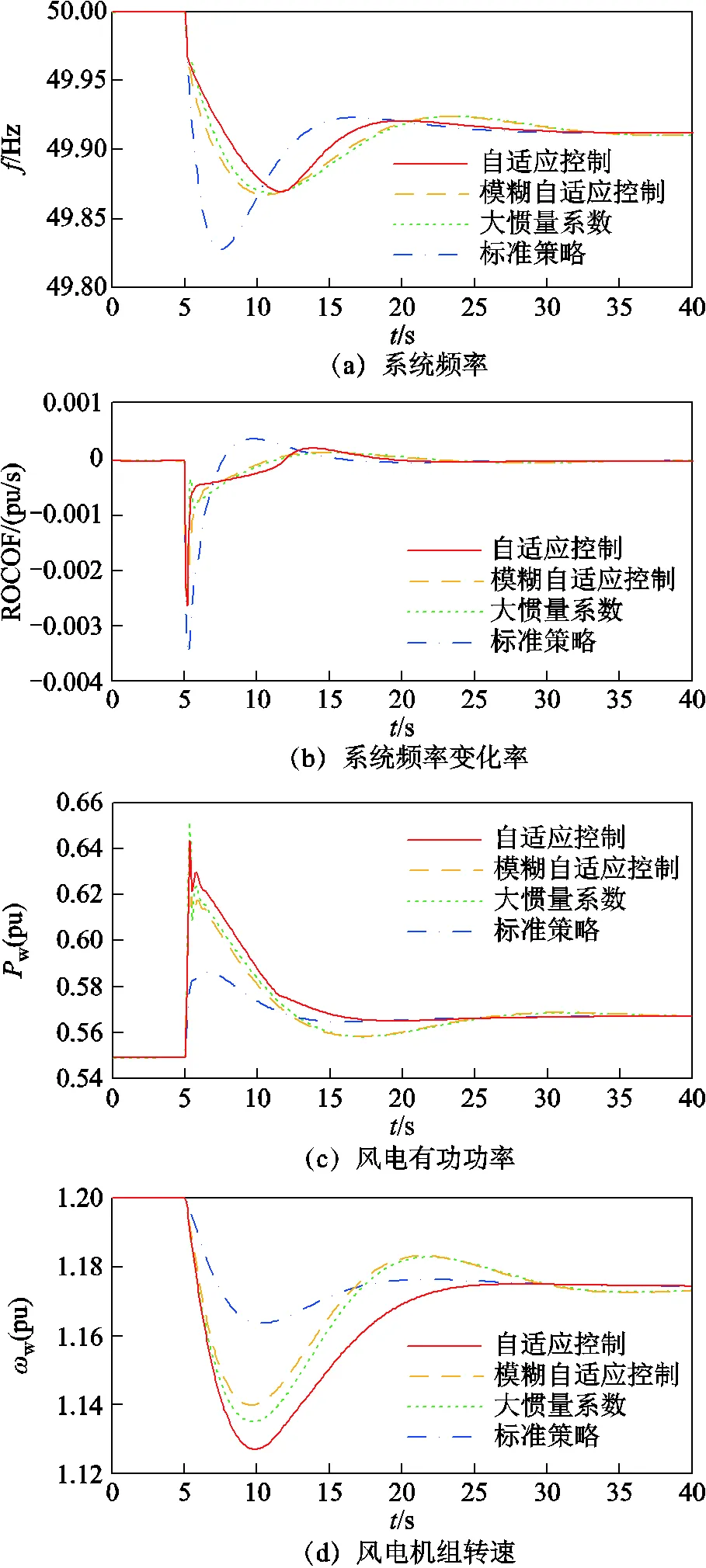
风电场在中、高风速下释放动能的能力充足,在系统受到大扰动时能提供强惯量支撑。从图10a及表4中可以看出,=5 s时系统发生扰动,自适应惯量控制系统频率在=11.7 s时跌落至最低点49.870 Hz,比其他三种控制策略的跌落深度小且到达最低点的时间更长,跌落更缓慢,跌落时间分别比大惯量系数控制和模糊自适应控制长0.8 s(13.6%)和1.2 s(21.8%),能够为其他调频措施的响应争取时间。从图10c中可以看出,自适应惯量控制在频率跌落时提供较大的有功功率支撑,而稳态时由于一次调频系数相同,四种控制策略的一次调频功率相同。结合图10b和图10c可以看出,系统频率变化率在扰动初始时刻超过了-0.04 Hz/s,自适应惯量系数快速升高;对比图8b和图8e,在系统受到小扰动时,自适应惯量系数升高幅度较小,验证了所设计的自适应惯量系数可以根据受扰动大小而改变。由于风速较高,风电机组转子存储的动能更多,根据图10 d可知,采用自适应惯量控制时风电机组转子转速跌落幅度最大,释放了更多动能,对风电惯量支撑能力的利用更充分。根据图10e可知,自适应惯量控制的惯量系数在=5 s扰动发生后迅速升至150(pu),约为大惯量系数控制的2倍,但由于风电有功爬坡率最大为0.45(pu)/s[13],风电出力增量并没有达到其他控制策略2倍的水平。
表4 高风速大扰动仿真结果

Tab.4 Simulation results with high wind speed and large disturbance
4.4 不同风电渗透率场景
为进一步验证所提自适应惯量控制策略的有效性,增加了风电渗透率为12%和50%的算例分析。考虑到连续扰动包含了阶跃和斜坡扰动也更贴合实际,且4.3节中设置的低风速大扰动场景会出现退出调频的现象,需要观察渗透率变化后所提自适应惯量控制是否仍能保证风电机组转速在安全范围内运行。因此,给出了风电渗透率为12%和50%时中风速连续扰动和低风速大扰动场景下系统的频率响应特性,除风电场容量、风速和系统所受扰动之外的其他参数与4.3节相同。
不同渗透率下风电并网系统多场景频率响应曲线如图11所示。通过对比图9a、图11e和图11f可以看出,当风电退出调频后,风电渗透率为50%时系统的频率的跌落幅度更深,跌落时间更长,说明风电渗透率越高,风电场对于电力系统频率特性的影响越显著。在此场景下模糊自适应控制和大惯量系数控制的风电场因转速跌至0.7(pu)导致退出调频,由于传统机组占比减小,频率二次跌落的幅度也更大。因此风电渗透率越高,考虑风电惯量支撑能力的意义也更重要。

不同渗透率下风电自适应惯量系数曲线如图12所示。通过对比图11b~图11d和图12中=7~13 s曲线可以看出,随着渗透率提升,相同扰动下风电提供惯量支撑所需的惯量系数更小,这是因为控制系统中的控制信号均为标幺值,风电装机容量提升后更小的惯量系数即可实现相似效果的惯量支撑。因此,大惯量系数控制中由于惯量系数为常数,其在渗透率为50%时实际惯量支撑功率比渗透率35%和12%更高,这也是导致图11d中=12 s时自适应惯量控制的频率跌落最低值比大惯量系数低,而渗透率为12%时(图11b)跌落最低值几乎相同的原因,该现象说明自适应惯量控制策略能根据风电渗透率自适应地调整支撑强度。
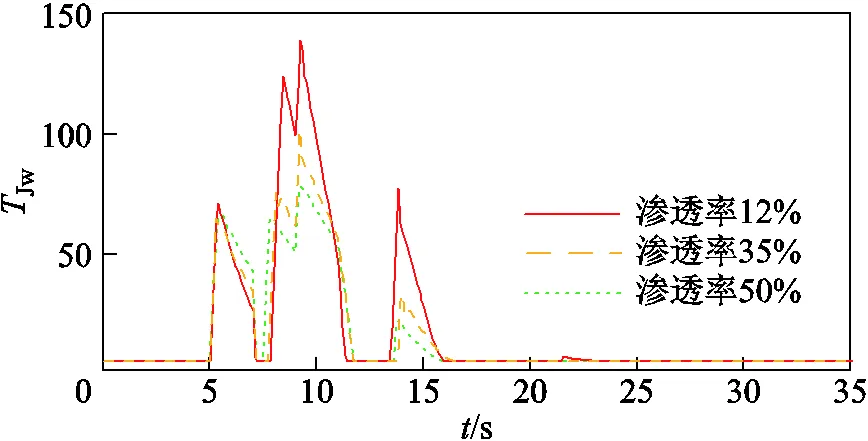
图12 不同渗透率下风电自适应惯量系数曲线
综合仿真分析结果可以看出:考虑双向支撑能力的自适应惯量控制策略在低风速下能保证风电运行在安全转速范围,在高风速大扰动仿真场景下能提供有力惯量支撑,能有效延缓系统的频率跌落,在中风速下能达到与模糊自适应控制相似的控制效果。即本文所提策略会根据风电机组的不同工况自适应地改变惯量系数,保证风电机组正常运行的同时提供其能力范围内的惯量支撑。同时,可以根据系统频率的变化率和变化方向自适应地改变惯量系数,实现了考虑系统实际需求的合理的惯量支撑。
5 结论
本文针对并网风电系统提出了一种自适应惯量控制策略,使得风电机组能够为系统提供更加灵活、合理的惯量支撑,具体结论如下:
1)通过定量分析风电机组在不同风速区间和不同转速下的动能吸收/释放能力,给出了风电机组的动能吸收/释放能力曲线,发现风机在中风速的动能吸收/释放能力均较其他风速区间更强,且在高风速下风机无法吸收动能。当规定风机对频率上升/下跌事件的功率调节裕度相同时,在中、高风速区间内其对频率下降的惯量支撑能力比频率上升事件更强。
2)提出了能够根据风电机组自身惯量支撑能力和系统惯量支撑需求自适应地修改虚拟惯量系数的自适应惯量控制策略,所设计的自适应惯量控制参数能够确保闭环控制系统的小扰动稳定,同时使得风电机组具备良好的频率动态特性。
3)相同渗透率不同风速和扰动下的仿真结果表明,所提自适应惯量控制策略能在低风速下降低惯量系数以保证风电运行在安全转速范围内,在中风速下能够提供与模糊自适应控制相当的惯量支撑效果,在高风速大扰动下能够提供有力惯量支撑,频率跌落速度比已有典型控制策略有所减小。不同渗透率下的仿真结果表明,基于减载的稳态工况,所提自适应惯量控制策略在算例场景中均能保证风电机组转速在安全范围内运行,且能随着渗透率的提高自适应地调整惯量系数以匹配风电惯量支撑能力和系统惯量支撑需求。
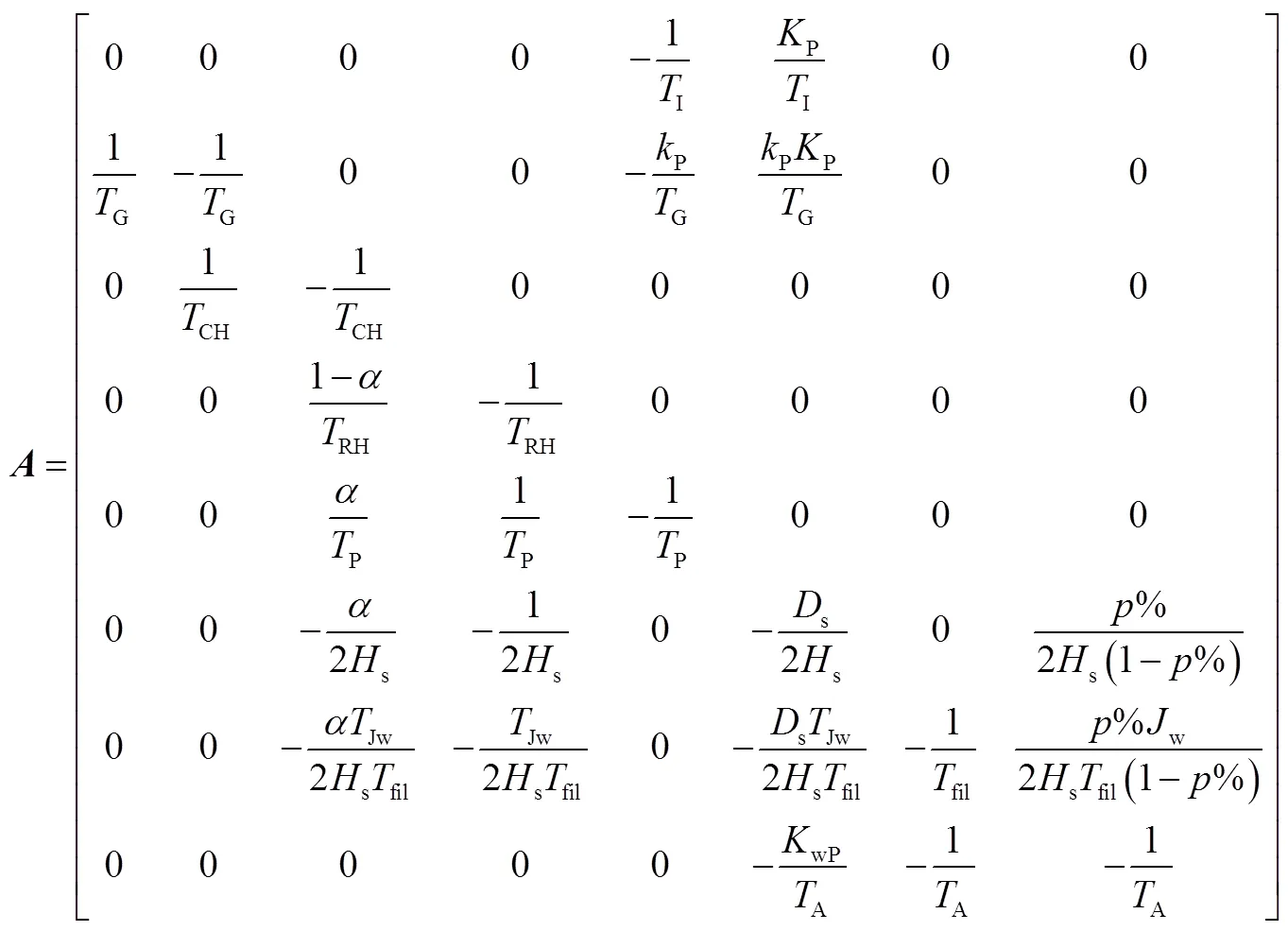
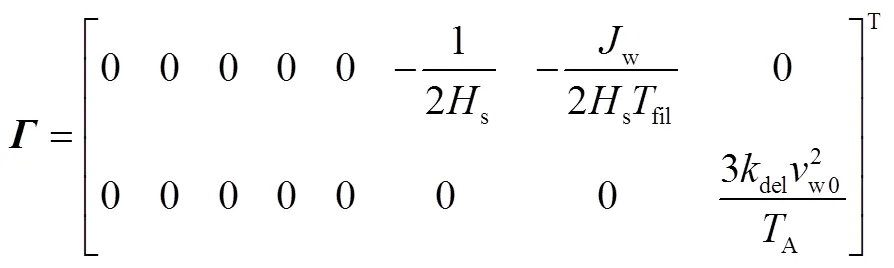
[1] 汪梦军, 郭剑波, 马士聪, 等. 新能源电力系统暂态频率稳定分析与调频控制方法综述[J]. 中国电机工程学报, 2023, 43(5): 1672-1693. Wang Mengjun, Guo Jianbo, Ma Shicong, et al. Review of transient frequency stability analysis and frequency regulation control methods for renewable power systems[J]. Proceedings of the CSEE, 2023, 43(5): 1672-1693.
[2] 高丙团, 胡正阳, 王伟胜, 等. 新能源场站快速有功控制及频率支撑技术综述[J/OL]. 中国电机工程学报, 2023: 1-16. http://kns.cnki.net/kcms/detail/11.2107. TM.20230530.1551.003.html. Gao Bingtuan, Hu Zhengyang, Wang Weisheng, et al. review on fast active power control and frequency support technologies of renewable energy stations [J/OL]. Proceedings of the CSEE, 2023: 1-16. http:// kns.cnki.net/kcms/detail/11.2107.TM.20230530.1551. 003.html.
[3] 张祥宇, 胡剑峰, 付媛, 等. 风储联合系统的虚拟惯量需求与协同支撑技术[J/OL]. 电工技术学报, 2023: 1-14. DOI:10.19595/j.cnki.1000-6753.tces. 221977. Zhang Xiangyu, Hu Jianfeng, Fu Yuan, et al. Virtual inertia demand and collaborative support technology of wind power and energy storage system[J/OL]. Transactions of China Electrotechnical Society, 2023: 1-14. DOI: 10.19595/j.cnki.1000-6753. tces.221977.
[4] 程鹏, 马静, 李庆, 等. 风电机组电网友好型控制技术要点及展望[J]. 中国电机工程学报, 2020, 40(2): 456-466. Cheng Peng, Ma Jing, Li Qing, et al. Key points and prospect of grid-friendly control technology for wind turbines[J]. Proceedings of the CSEE, 2020, 40(2): 456-466.
[5] 颜湘武, 王德胜, 杨琳琳, 等.直驱风机惯量支撑与一次调频协调控制策略[J]. 电工技术学报, 2021, 36(15): 3282-3292. YanXiangwu, Wang Desheng, Yang Linlin, et al. Coordinated control strategy of inertia support andprimary frequency regulation of PMSG[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3282-3292.
[6] 李少林, 王伟胜, 张兴, 等. 基于频率响应区间划分的风电机组虚拟惯量模糊自适应控制[J]. 电网技术, 2021, 45(5): 1658-1664. Li Shaolin, Wang Weisheng, Zhang Xing, et al. Fuzzy adaptive virtual inertia control strategy of wind turbines based on system frequency response interval division[J]. Power System Technology, 2021, 45(5): 1658-1664.
[7] 国家市场监督管理总局, 国家标准化管理委员会. 风电场接入电力系统技术规定第1部分:陆上风电: GB/T 19963.1—2021[S]. 北京: 中国标准出版社, 2021.
[8] Kheshti M, Lin Shuyue, Zhao Xiaowei, et al. Gaussian distribution-based inertial control of wind turbine generators for fast frequency response in low inertia systems[J]. IEEE Transactions on Sustainable Energy, 2022, 13(3): 1641-1653.
[9] 张冠锋, 杨俊友, 孙峰, 等. 基于虚拟惯量和频率下垂控制的双馈风电机组一次调频策略[J]. 电工技术学报, 2017, 32(22): 225-232. Zhang Guanfeng, Yang Junyou, Sun Feng, et al. Primary frequency regulation strategy of DFIG based on virtual inertia and frequency droop control[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 225-232.
[10] Hwang M, Muljadi E, Jang G, et al. Disturbance-adaptive short-term frequency support of a DFIG associated with the variable gain based on the ROCOF and rotor speed[J]. IEEE Transactions on Power Systems, 2017, 32(3): 1873-1881.
[11] Lee J, Jang G, Muljadi E, et al. Stable short-term frequency support using adaptive gains for a DFIG-based wind power plant[J]. IEEE Transactions on Energy Conversion, 2016, 31(3): 1068-1079.
[12] 李颖颖, 王德林, 范林源, 等. 双馈风电机组限功率运行下频率稳定的变系数控制策略[J]. 电网技术, 2019, 43(8): 2910-2917. Li Yingying, Wang Delin, Fan Linyuan, et al. Variable coefficient control strategy for frequency stability of DFIG under power-limited operation[J]. Power System Technology, 2019, 43(8): 2910-2917.
[13] Wu Yuankang, Yang Wuhan, Hu Yiliang, et al. Frequency regulation at a wind farm using time-varying inertia and droop controls[J]. IEEE Transactions on Industry Applications, 2019, 55(1): 213-224.
[14] 林俐, 李晓钰, 王世谦, 等. 基于分段控制的双馈风电机组有功-频率控制[J]. 中国电力, 2012, 45(2): 49-53. Lin Li, Li Xiaoyu, Wang Shiqian, et al. An active power-frequency control strategy of a DFIG based on subsection control[J]. Electric Power, 2012, 45(2): 49-53.
[15] 颜湘武, 崔森, 常文斐. 考虑储能自适应调节的双馈感应发电机一次调频控制策略[J]. 电工技术学报, 2021, 36(5): 1027-1039. Yan Xiangwu, Cui Sen, Chang Wenfei. Primary frequency regulation control strategy of doubly-fed induction generator considering supercapacitor SOC feedback adaptive adjustment[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 1027-1039.
[16] Hwang M, Muljadi E, Park J W, et al. Dynamic droop-based inertial control of a doubly-fed induction generator[J]. IEEE Transactions on Sustainable Energy, 2016, 7(3): 924-933.
[17] 周天沛, 孙伟. 高渗透率下变速风力机组虚拟惯性控制的研究[J]. 中国电机工程学报, 2017, 37(2): 486-495. Zhou Tianpei, Sun Wei. Study on virtual inertia control for DFIG-based wind farms with high penetration[J]. Proceedings of the CSEE, 2017, 37(2): 486-495.
[18] 柯贤波, 张文朝, 李朋旺, 等. 高风电渗透率系统的模糊自适应虚拟惯量控制[J]. 电网技术, 2020, 44(6): 2127-2134. Ke Xianbo, Zhang Wenchao, Li Pengwang, et al. Fuzzy adaptive virtual inertia control for high wind power penetration system[J]. Power System Technology, 2020, 44(6): 2127-2134.
[19] Li Meiyi, Huang Wentao, Tai Nengling, et al. A dual-adaptivity inertia control strategy for virtual synchronous generator[J]. IEEE Transactions on Power Systems, 2020, 35(1): 594-604.
[20] Lü Xue, Jia Youwei, Xu Zhao. A novel control strategy for wind farm active power regulation considering wake interaction[J]. IEEE Transactions on Sustainable Energy, 2020, 11(2): 618-628.
[21] 穆钢, 蔡婷婷, 严干贵, 等. 双馈风电机组参与持续调频的双向功率约束及其影响[J]. 电工技术学报, 2019, 34(8): 1750-1759. Mu Gang, Cai Tingting, Yan Gangui, et al. Bidirectional power constraints and influence of doubly fed induction generator participating in continuous frequency regulation[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1750-1759.
[22] 毛永恒, 高丙团, 胡正阳, 等. 计及双馈机组直流卸荷的风电场紧急降功率控制策略[J/OL]. 中国电机工程学报, 2023: 1-5. http://kns.cnki.net/kcms/ detail/11.2107.tm. 20230619.1644.003.html MaoYongheng, Gao Bingtuan, Hu Zhengyang, et al. emergency power reduction control strategy of wind farm considering DC chopper of doubly-fed induction generator[J/OL]. Proceedings of the CSEE, 2023: 1-15. http:// kns.cnki.net/kcms/detail/11.2107.tm.20230619. 1644.003.html.
[23] 胡家欣, 胥国毅, 毕天姝, 等. 减载风电机组变速变桨协调频率控制方法[J]. 电网技术, 2019, 43(10): 3656-3662. Hu Jiaxin, Xu Guoyi, Bi Tianshu, et al. A strategy of frequency control for deloaded wind turbine generator based on coordination between rotor speed and pitch angle[J]. Power System Technology, 2019, 43(10): 3656-3662.
[24] 刘昊宇, 刘崇茹, 董浩云. 含风电场的MMC-MTDC系统通用频率响应模型[J]. 电力系统自动化, 2023, 47(5): 123-133. Liu Haoyu, Liu Chongru, Dong Haoyun. General frequency response model of MMC-MTDC system integrated with wind farms[J]. Automation of Electric Power Systems, 2023, 47(5): 123-133.
[25] 耿华, 许德伟, 吴斌, 等. 永磁直驱变速风电系统的控制及稳定性分析[J]. 中国电机工程学报, 2009, 29(33): 68-75. Geng Hua, Xu Dewei, Wu Bin, et al. Control and stability analysis for the permanent magnetic synchronous generator based direct driven variable speed wind energy conversion system[J]. Proceedings of the CSEE, 2009, 29(33): 68-75.
[26] 王刚, 侍乔明, 崔志勇, 等. 一种风力机虚拟惯量控制与传统发电机调速控制的协调方法[J]. 电网技术, 2015, 39(10): 2794-2801. Wang Gang, Shi Qiaoming, Cui Zhiyong, et al. A coordinated strategy of virtual inertia control of wind turbine and governor control of conventional generator[J]. Power System Technology, 2015, 39(10): 2794-2801.
[27] Mauricio J M, Marano A, Gomez-Exposito A, et al. Frequency regulation contribution through variable-speed wind energy conversion systems[J]. IEEE Transactions on Power Systems, 2009, 24(1): 173-180.
[28] 滕贤亮, 谈超, 昌力, 等. 高比例新能源电力系统有功功率与频率控制研究综述及展望[J]. 电力系统自动化, 2023, 47(15): 12-35. Teng Xianliang, Tan Chao, Chang Li, et al. Review and prospect of research on active power and frequency control in power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2023, 47(15): 12-35.
[29] 奥博宇, 王方政, 陈磊, 等. 风电机组变桨减载一次调频模型及聚合方法[J]. 电网技术, 2023, 47(4): 1360-1368. Ao Boyu, Wang Fangzheng, Chen Lei, et al. Primary frequency regulation model and aggregation of deloading wind turbine generators with pitch angle adjustment[J]. Power System Technology, 2023, 47(4): 1360-1368.
[30] 李世春, 吕翔生, 钟浩, 等. 大规模双馈风电机组参与调频的电网自适应低频减载策略[J]. 电力系统自动化, 2019, 43(15):109-115. Li Shichun, Lv Xiangsheng, Zhong Hao, et al. adaptive under-frequency load shedding strategy of power grid with large-scale DFIG wind turbines participating in frequency regulation[J]. Automation of Electric Power Systems, 2019, 43(15): 109-115.
[31] Li Yujun, Xu Zhao, Zhang Jianliang, et al. Variable utilization-level scheme for load-sharing control of wind farm[J]. IEEE Transactions on Energy Conversion, 2018, 33(2): 856-868.
[32] 王鑫, 杨德健. 基于变系数PI控制的双馈风电机组自适应转速恢复策略[J]. 电工技术学报, 2023, 38(15): 4120-4129. Wang Xin, Yang Dejian. Adaptive speed recovery strategy of doubly-fed induction generator based on variable PI control coefficient[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4120-4129.
[33] 张正阳, 殷明慧, 李阳, 等. 考虑机组稳定约束的风机一次调频控制策略[J]. 中国电机工程学报, 2023, 43(4): 1471-1480. Zhang Zhengyang, Yin Minghui, Li Yang, et al. Turbine stability-constrained primary frequency control of wind turbine generator[J]. Proceedings of the CSEE, 2023, 43(4): 1471-1480.
[34] Dreidy M, Mokhlis H, Mekhilef S. Inertia response and frequency control techniques for renewable energy sources: a review[J]. Renewable and Sustainable Energy Reviews, 2017, 69: 144-155.
[35] Wang Ye, Delille G, Bayem H, et al. High wind power penetration in isolated power systems—assessment of wind inertial and primary frequency responses[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2412-2420.
[36] 李兆伟, 吴雪莲, 庄侃沁, 等. “9·19”锦苏直流双极闭锁事故华东电网频率特性分析及思考[J]. 电力系统自动化, 2017, 41(7): 149-155. Li Zhaowei, Wu Xuelian, Zhuang Kanqin, et al. Analysis and reflection on frequency characteristics of East China grid after bipolar locking of “9·19” Jinping-Sunan DC transmission line[J]. Automation of Electric Power Systems, 2017, 41(7): 149-155.
[37] 张祥宇, 朱永健, 付媛. 基于系统惯量需求的风储协同快速频率响应技术[J]. 中国电机工程学报, 2023, 43(14): 5415-5429. ZhangXiangyu, Zhu Yongjian, Fu Yuan. wind-storage cooperative fast frequency response technology based on system inertia demand[J]. Proceedings of the CSEE, 2023, 43(14): 5415-5429.
Bidirectional Support Capability Analysis and Adaptive Inertial Control Strategy of Wind Turbine
Hu Zhengyang1Gao Bingtuan1Zhang Lei2Wang Wenzhuo3Pan Shenkai1
(1. School of Electrical Engineering Southeast University Nanjing 210096 China 2. National Key Laboratory of Renewable Energy Grid-Integration China Electric Power Research Institute Nanjing 210003 China 3. Northwest Branch of State Grid Corporation of China Xi’an 710048 China)
Inertial response is one of the fast-transient frequency support control methods. In the latest wind farm grid-connected technical specification in China, wind farms are required to have inertial response capabilities. However, the current research on the design of inertial control parameters still needs investigation. When evaluating the kinetic energy stored in the rotor of the wind turbine, the existing literature mostly takes the difference between the current speed and the lower limit of the speed as the baseline value, which makes the speed of the wind turbine drop to the left side of the MPPT point, jeopardizing the small disturbance stability of the wind turbine. In addition, the current research mostly focuses on solving the inertial support of frequency drop events, while ignoring the problem of insufficient power reduction capacity of wind turbines with low wind speed and high wind speed. To address these issues, this paper proposes an adaptive inertial control strategy for wind turbine considering bidirectional support capability for wind power integrated power system.
Firstly, based on the typical model of power system integrated with wind power generation, the frequency dynamic response characteristics of the system with different wind power penetrations, control parameters and disturbances were analyzed. Secondly, considering the relationship curves of wind power output and rotor speed, the inertial support capability of wind turbines to frequency rise and drop events was analyzed quantitatively. Thirdly, the adaptive inertial control strategy of wind power generation was proposed.An adaptive inertia coefficient with upper and lower limits, left and right symmetry and adjustable sensitivity to the rate of change of frequency was designed. The upper limit was determined by the inertial support capability evaluation using the Newton-Raphson method, the lower limit was set based on the Chinese national standard, and the sensitivity coefficient was designed according to the inertial support requirement of power system. Finally, the small-signal stability of the control system was analyzed according to the eigenvalue loci.
The simulation results show that the proposed adaptive inertial control strategy can reduce the inertia coefficient at low wind speed to ensure that the wind turbine operates within the safe speed range. It can provide strong inertial support with high wind speed and large disturbance, and the frequency drop depth is smaller than the existing typical control strategies. Besides, the proposed adaptive inertia control strategy can ensure that the wind turbine operates within a safe rotor speed range based on the steady-state condition of deloading and can adaptively adjust the inertia coefficient with the increase of the wind power penetration to match the wind power inertial support capability and power system inertial support requirements.
Through this investigation, the following conclusions are drawn: (1) Through quantitatively analyzing the kinetic energy absorption/release capacity of the wind turbine, it is indicated that the kinetic energy absorption/release capacity of the wind turbine at medium wind speed is stronger than that at other wind speed ranges, and the wind turbine cannot absorb kinetic energy at high wind speed. (2) Provided that the power regulation range of the wind turbine for frequency rise/drop events is the same, the inertial supportcapability of the wind turbine for frequency drop is stronger than that for frequency rise events in the middle and high wind speed ranges. (3) Simulation results show that compared with the existing typical strategies, the proposed strategy can improve the frequency characteristics of scenarios with low and high wind speed.
Wind turbine, inertial support, frequency characteristics, adaptive control, small-signal analysis
10.19595/j.cnki.1000-6753.tces.230981
TM614; TM712
国家电网公司总部科技项目资助(4000-20236084A-1-1-ZN)。
2023-06-25
2023-08-09
胡正阳 男,1994年生,博士研究生,研究方向为新能源发电并网控制等。E-mail:huzhengyang@seu.edu.cn
高丙团 男,1981年生,博士,教授,博士生导师,研究方向为机器人与智能电力运维、新能源发电并网控制、分布式供能与需求响应等。E-mail:gaobingtuan@seu.edu.cn(通信作者)
(编辑 郭丽军)

