基于RE-GAN的调制信号开集识别算法

秦博伟, 蒋 磊, 许 华, 牛伟宇

(空军工程大学信息与导航学院, 陕西 西安 710077)

0 引 言

信号的调制方式是区分不同信号类型的一个重要特征。非协作信号接收系统中,调制方式识别在信号解调、频谱检测和参数估计等方面起着至关重要的作用[1]。

目前,调制识别方法可区分为两大类:传统的调制识别方法和基于深度学习的自动调制识别算法。传统的调制识别方法又分为基于似然比决策理论的识别方法和基于特征提取的统计模式识别方法。前者根据信号的统计特性,依据代价函数最小化原则,通过理论分析与推导得到检验统计量,再将其与一个合适的门限进行比较,形成判决准则,最后由判决准则确定输出结果,完成通信信号调制方式的分类识别,判决准则一般有最大似然比[2-3]、广义平均似然比[4]等。后者主要分为特征提取和模式识别两个部分,目前有基于高阶累积量[5]、基于小波变换[6]、基于时频分析[7]和基于谱相关理论[8]等特征的识别方法。传统的调制识别方法需要根据信号特点人工设置门限或者分类器,受人为不确定因素影响较大。

文献[9]提出一种不需要人工设计特征和判决门限的自动调制识别算法,该算法将深度学习中的卷积神经网络(convolutional neural networks, CNN)应用到调制识别领域,首次实现调制信号端到端的识别模型。在这之后,大量的神经网络模型被应用于自动调制识别领域[10-12]。文献[13]结合多种网络,利用信号的多维度特征,在信噪比(signal to noise ratio, SNR)为4 dB时对11种调制方式的识别准确率可以达到90%。文献[14-15]则利用生成对抗网络(generative adversarial network, GAN)[16]初步实现了少量样本条件下的信号调制识别尽管在调制识别领域已经取得了一定的成果,但面对日益复杂的电磁环境和层出不穷的新式调制样式,闭集识别的模式已经逐渐不再适用,如何在开放式环境下准确判断出新式调制样式已经成为当下研究的热点。文献[17]首次提出openmax开集识别算法,提出一种“距离矢量”作为区分各个类别之间的标准,在MINST公开数据集上测试可以达到92%的识别准确率。文献[18]则利用GAN生成未知类别的虚假数据供网络进行特征学习,较原始的openmax算法性能提升3%～5%。

针对调制信号开集识别的问题[1],本文从数据重建和极值理论(extreme value theory, EVT)的角度出发,设计了一种数据重建和EVT的GAN (reconstructed data and EVT GAN, RE-GAN)模型,通过建立信号间的激活矢量集来区分不同调制信号。首先通过重建网络(reconstructed network, R)和判别网络(discriminant network,D)建立不同类别信号的激活矢量集,而后将激活矢量拟合到特定的极值分布中并选择合适的距离矢量度量已知调制方式和未知调制方式与激活矢量中心的距离,最后依据EVT判别出已知和未知调制方式的信号。仿真实验证明,本文所提算法较以往的开集识别算法性能提升3%～7%,网络模型更具轻量化。

1 RE-GAN

1.1 网络模型设计

RE-GAN的网络模型设计参考GAN模型架构,R和D进行交替对抗训练。R对真实数据进行压缩重建,将高维信息压缩为低维表示,输出压缩向量(真实数据)和重建数据(虚假数据)。D则需要准确地区分数据的类别属性和真假属性。通过D的输出反馈到前置网络实现网络的训练。

RE-GAN的网络结构分为训练阶段和测试阶段,模型架构如图1和图2所示。

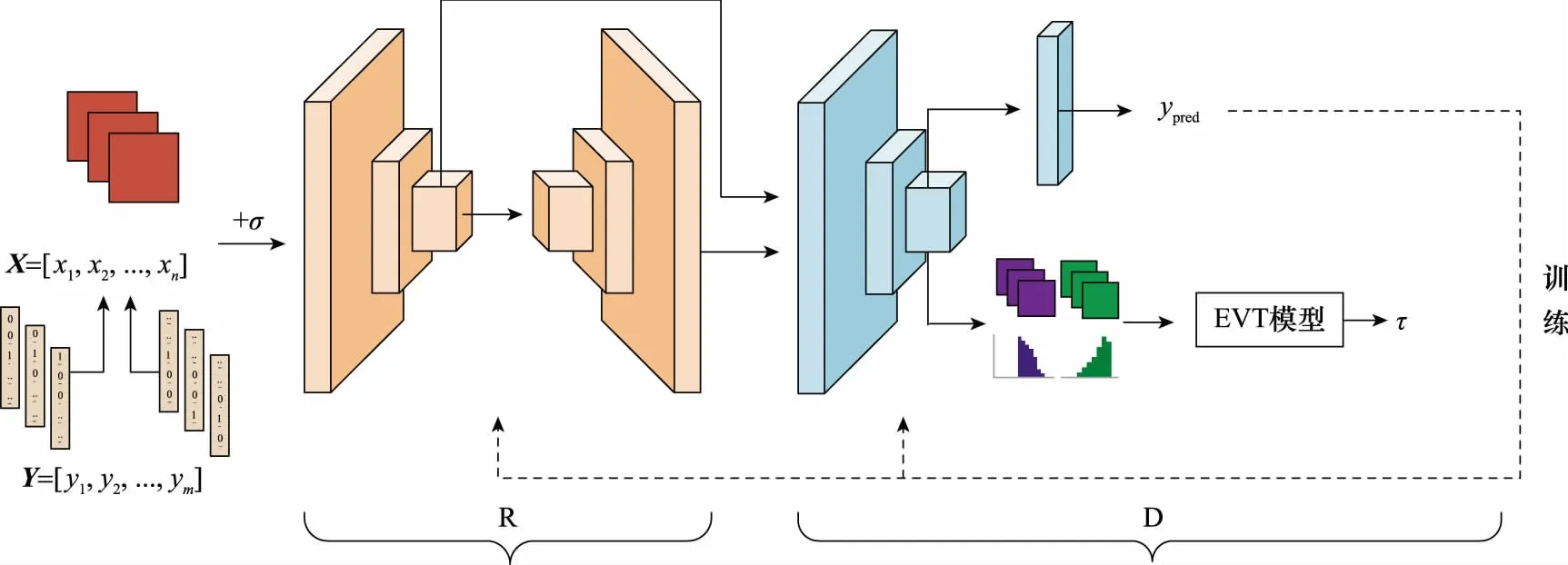
图1 RE-GAN训练网络Fig.1 Train network of RE-GAN

图2 RE-GAN测试网络Fig.2 Test network of RE-GAN

其中,X为训练数据,Y代表训练数据的类别标签,σ代表噪声,τ代表训练阶段根据EVT求出的阈值。X′为测试数据,Y′代表测试数据的类别标签,Reri(i=1,2,3,…,k)代表D倒数第二层输出的每一类数据的平均激活矢量(mean activation vector, MAV),ypred代表已知类别的预测标签,yuk代表未知类别。

1.2 数据预处理

数据预处理模块主要针对数据的幅值信息和相位信息进行归一化,假设原始数据为x,归一化后的数据为x′,则

(1)

式中:A为幅值;φ为相位;I和Q分别表示解调后的同相数据和正交数据;min和max分别为x所在列的最小值和最大值。对数据进行归一化的目的是为了消除数据之间的量纲影响,避免数值相差太大导致神经网络训练困难,方便后续网络进行计算。

2 基于RE-GAN的开集识别算法

2.1 开集识别理论

闭集识别问题即测试和训练的每个类别都有具体的标签,不包含未知的类别; 如著名的MNIST和MNIST_FASHION数据集,里面包含确定的类别。以MNIST数据集为例,训练时包含0～9的数字类别,测试时也是0～9的类别,并不包含如字母A～Z等的未知类别,闭集识别问题即区分这10个类别。而开集识别问题训练阶段保持不变,测试时不仅仅包含0～9的数字类别,还包含其他如A～Z等的未知类别,但是这些未知的类别并没有标签,分类器无法知道这些未知类别里面图像的具体类别,如是否是A,所有未知的图像共同构成了一个未知类别,开集分类问题即区分这10个类别且拒绝其他未知类别。开集识别与闭集识别的决策边界如图3所示。从图3中可以看到,闭集识别的决策边界一定会把未知类别判定为已知类别中确定的一类,而开集识别的决策边界则会将所有未知类别都划分为单独的一类。

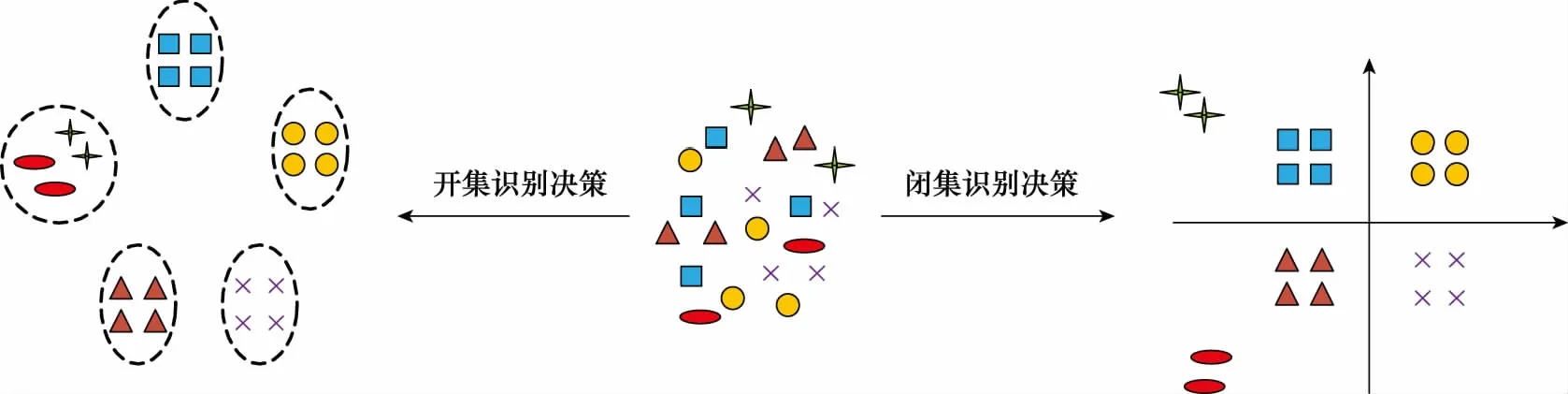
图3 开集识别和闭集识别的决策边界Fig.3 Decision boundary of open-set recognition and closed-set recognition

假设有N类数据,K={C1,C2,…,CN},输入数据为x,Softmax函数定义为

(2)

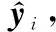
(3)

式中:wi表示p(Ci|x,x∈K),第N+1类表示未知类别。具体的训练过程[19]为:在训练阶段,首先训练一个Softmax函数的神经网络,然后依据最近类平均理论[20],在倒数第二层输出计算各类样本输出矢量的均值并得到各类样本的MAV,而后选定一个距离度量函数度量训练样本与对应类别MAV之间的距离并拟合到Weibull分布,Weibull分布是连续性的概率分布函数,对于服从统一分布的不同样本数据X,可以通过拟合Weibull 分布来建立不同样本间的模型,方便后续利用EVT进行概率计算),最后保存MAV集合和Weibull分布模型。在测试阶段,首先计算各个类别的测试样本在网络倒数第二层的输出矢量与各个类别MAV的距离,然后依据Weibull 分布拟合测试样本并更新MAV,最终根据EVT计算得出概率最大值为数据所对应的类别标签。

选择平均识别准确率作为开集识别模型的评价标准,具体公式如下:

(4)

式中:fkau和fukau分别代表已知类别和未知类别的分类准确率;m和n分别代表已知类和未知类的样本总数;p(xi)和yi分别代表数据的预测标签和真实标签;H(·)代表一个逻辑函数,当p(xi)与yi相同时取1,反之为0;对fkau和fukau取加权平均得到开集识别模型的分类准确率fau。

2.2 损失函数及网络参数设置

RE-GAN的损失函数分为两部分,第一部分为R的损失函数,第二部分为D的损失函数。具体表达式为

(5)

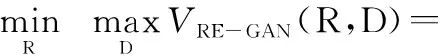
(6)

式中:E代表期望;R1和D1分别为R和D映射的可微函数;x和x1分别代表加噪前后的原始数据。依据GAN的目标优化函数准则[21-22],对目标函数求一个极大极小值,最终网络会收敛到一个纳什均衡点[16],即R的重建误差达到最小,D准确将数据进行分类。

图4为RE-GAN的具体网络参数设置。

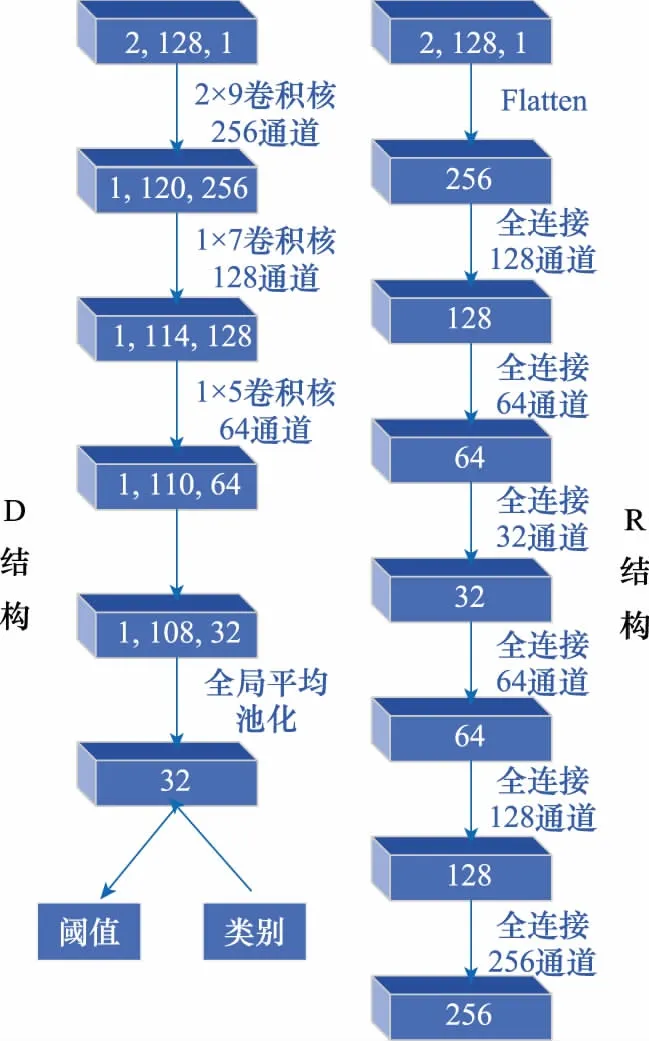
图4 R和D的网络参数设置Fig.4 Network parameter settings of R and D

R和D的网络结构选择与其他GAN结构不同,主要体现在3个方面。

(1) R选用自编码器对数据进行压缩重建,一方面降低了运算量并实现了数据的稀疏表达,另一方面压缩后的特征直接被利用于D,实现了特征的自动选择。

(2) D添加全局平均池化层,这样做的目的在于保留数据的空间结构信息,另外相比较于Flatten连接操作,网络参数明显降低,提高了网络的泛化性并防止网络过拟合。

(3) D卷积核大小均为卷积步幅为1的非对称卷积核,不仅可以最大限度地保留数据的原始信息,还可以分层次提取数据特征。

2.3 算法具体实现

步骤 1设置模型初始化参数。

步骤 2将标签数据x={(x1,y1),(x2,y2),…,(xm,ym)}送入R中执行梯度下降训练,输出重建数据x′={(x1,y1)′,(x2,y2)′,…,(xn,yn)′}和压缩向量l=[l1,l2,…,lk]。

步骤 3将l和x′一起送入到D中执行梯度下降,计算D倒数第二层每一类数据对应的MAV,选择余弦相似度度量函数度量训练数据与MAV之间的距离并拟合到Weibull分布模型中,并将最大的度量值记为阈值τ。最后输出数据的预测标签和τ。

步骤 4设置终止条件并保存MAV、Weibull分布模型、R和D的网络模型和权重。

步骤 5导入保存好的D模型和权重,将n个测试数据送入到D中进行测试,计算测试数据的MAV,更新倒数第二层的每一类数据的MAV,并将测试数据和MAV之间的度量距离拟合到Weibull分布并更新Weibull分布模型,记录每一类数据的度量值。

步骤 6将步骤5中输出的每一类度量值与步骤3中的τ值作对比,若最小值大于τ,则被划分为未知类别,否则划分为已知类别。被划分为已知类别的数据按照Openmax函数计算得到每一类数据的标签属性。

步骤 7输出最终分类结果。

3 实验仿真与结果分析

3.1 仿真环境及数据集

本文的网络模型训练均使用python的Keras环境,配置为Nvidia GTX 1650 GPU,借助Tensorflow后端进行训练,调制信号数据集采用Deepsig公开调制识别数据集[15]RML 2016.10b,本文采用的数据集信息如表1所示。

表1 调制信号数据集Table 1 Modulation signal dataset

为了适应开集识别的应用场景,对原始数据集信号进行切分处理,SNR范围-4～18 dB,选用除宽带调频(wide band frequency modulation, WBFM)和正交振幅调制(quadrature amplitude modulation, QAM)64 (QAM64)以外的8种信号作为模型训练时的数据,选用全部10种信号作为模型测试时的数据。

3.2 实验1:网络初始参数设置

为了方便模型进行卷积计算,将数据维度由(2,128)增加为(2,128,1),训练样本数量为115 200,测试样本数量为36 000。模型训练的epoch设置为20 000;batch-size设置为64;梯度优化算法选择Adam,学习率设为0.000 4,第一衰减率设为0.5;Dropout设置为0.1;隐藏层激活函数选择Leakyrelu激活函数,参数设置为0.3。网络采用交替迭代方式训练,先训练D,再训练R。

RE-GAN的损失函数曲线如图5和图6所示。

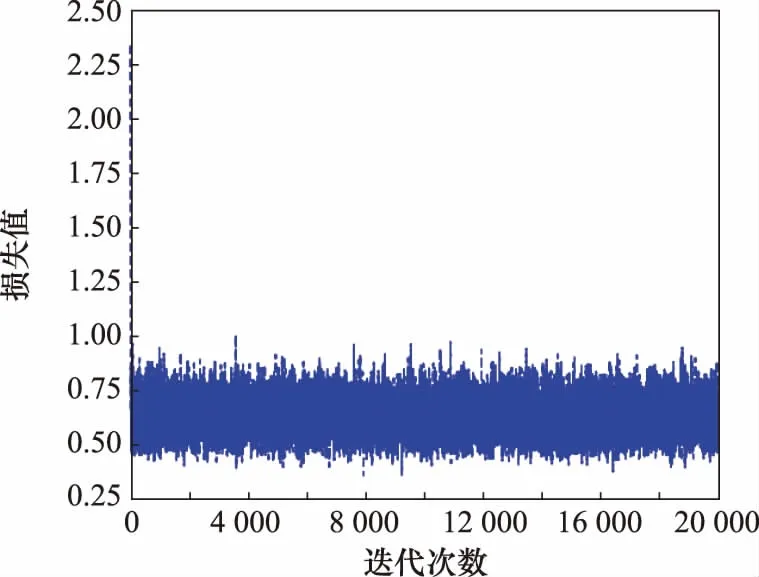
图5 D损失函数曲线Fig.5 D loss function curve

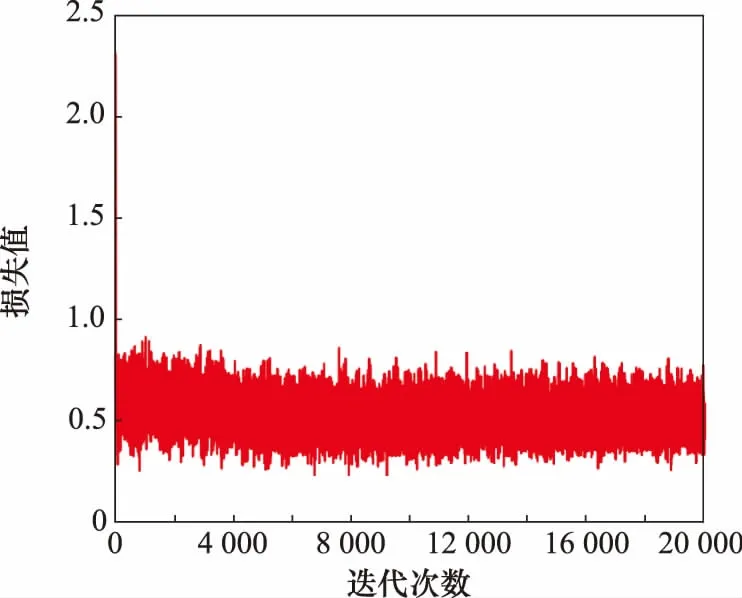
图6 R损失函数曲线Fig.6 R loss function curve

观察图5和图6损失函数曲线变化趋势,得出 R 和 D 的训练比较平稳,网络训练没有发生过拟合现象。

由于开集识别不仅需要分离出已知调制方式的信号,还需要拒绝未知类别的调制信号。因此,本文将不同调制方式经过网络输出后的MAV中心点用坐标画出来, 如图7所示。可以看出,各类别之间的MAV中心相差比较明显,侧面证明RE-GAN可以很好地分离出未知调制方式的信号。

图7 MAV中心点位置Fig.7 Location center of the MAV

为了验证所提算法的性能,本文还通过大量实验对比了不同激活函数、不同距离度量函数、有无全局平均池化层对模型性能的影响,具体结果如图8～图10所示(分类准确率为所有测试样本的平均分类准确率)。

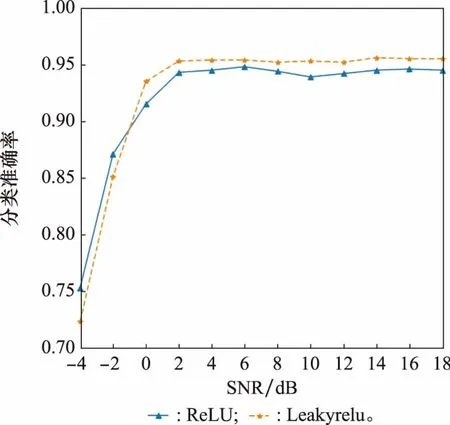
图8 不同激活函数Fig.8 Different activation functions

图9 不同距离度量函数Fig.9 Different distance measure functions

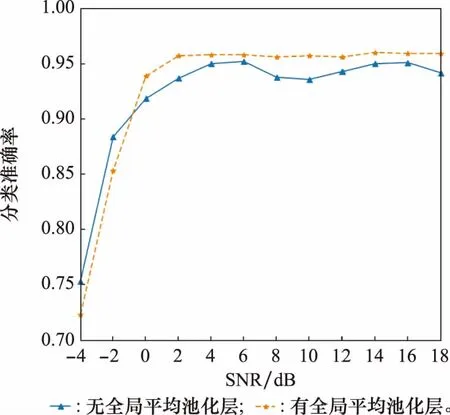
图10 有无全局平均池化层Fig.10 Global average pooling layer or not

观察图8可以得出Leakyrelu激活函数作用下的网络性能略高于ReLU激活函数。分析图9的结果可以得出,选用余弦相似度比选用欧式距离网络训练效果更好。对比图10的两条曲线,可以得出网络在添加全局平均池化层之后,稳定性更好,识别准确率略有提高。

3.3 实验2:调制信号分类识别

按照实验1的网络参数初始值设定和第2.3节的具体算法步骤,网络测试后的混淆矩阵如图11～图13所示(这里只对比闭集识别的混淆矩阵)。

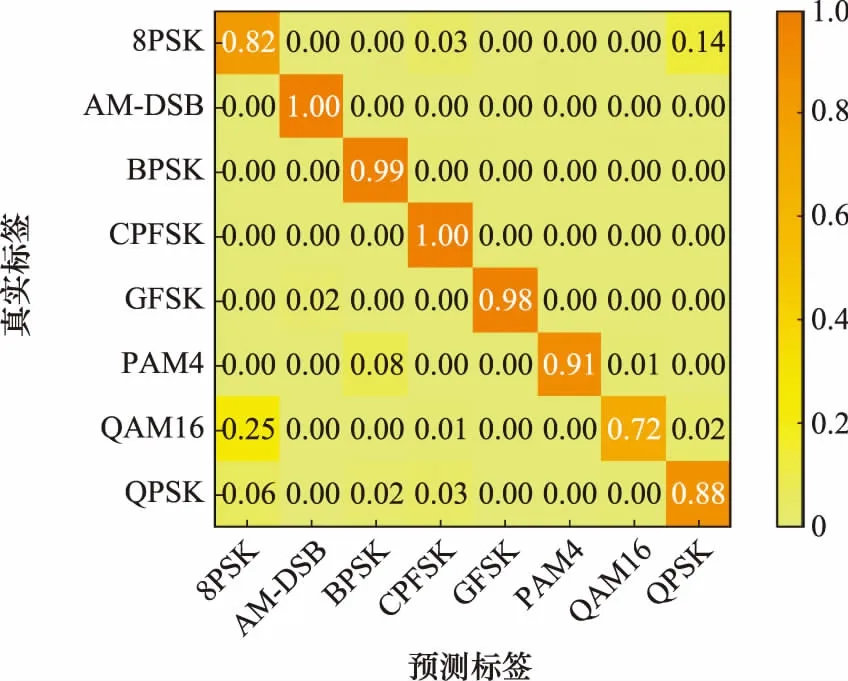
图11 混淆矩阵结果(SNR=0 dB)Fig.11 Confusion matrix result (SNR=0 dB)

图12 混淆矩阵结果(SNR=10 dB)Fig.12 Confusion matrix result (SNR=10 dB)

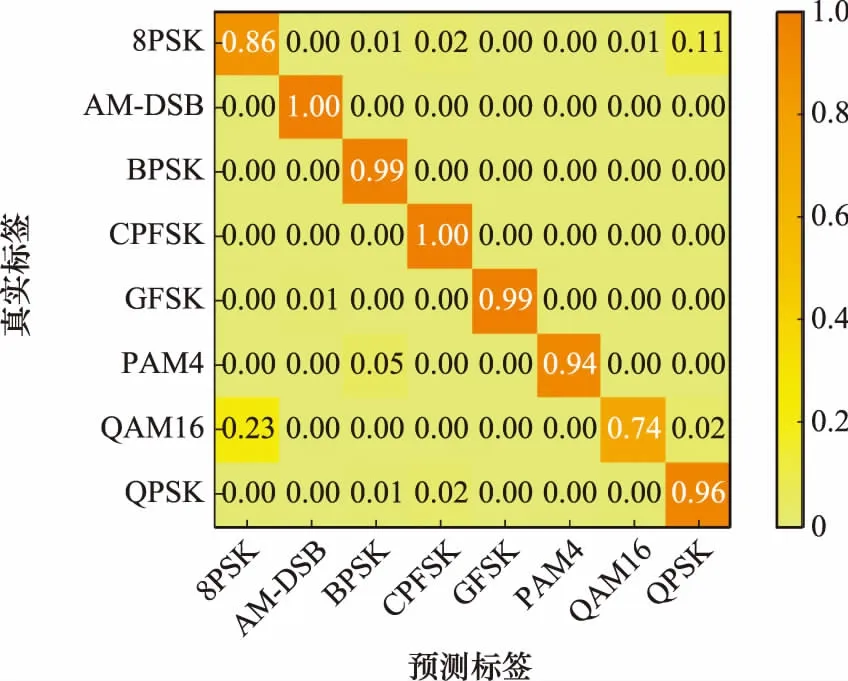
图13 混淆矩阵结果(SNR=18 dB)Fig.13 Confusion matrix result (SNR=18 dB)

对比图11～图13中3张混淆矩阵的结果图可以看出,RE-GAN模型在SNR大于0 dB时对已知信号的识别准确率可以达到93%,网络可以准确分离出已知调制样式的信号。

为了更好地说明本文所提算法的优势,分别对比了其他开集识别算法,具体实验结果如图14和表2所示。其中,不同算法包括了生成式对抗网络的开集识别(generative odversarial networks-openmax, G-Openmax)和开放式长尾识别(open-large-scale long-tailed recognition, OLTR)。分析图14和表2的实验结果可以得出,单独使用Softmax分类算法不能实现信号的开集识别,相比较于单独使用Softmax分类算法,RE-GAN的网络参数略有增加,闭集识别性能基本没有变化,说明本文所提算法可以有效实现调制信号的开集识别和闭集识别。相比较于另外3种开集识别算法,RE-GAN的网络参数和乘加次数均有所减少,识别准确率提升3%～7%。综上实验结果,基于RE-GAN的调制信号开集识别算法网络模型更具轻量化、训练时间更短、识别性能有所提高。

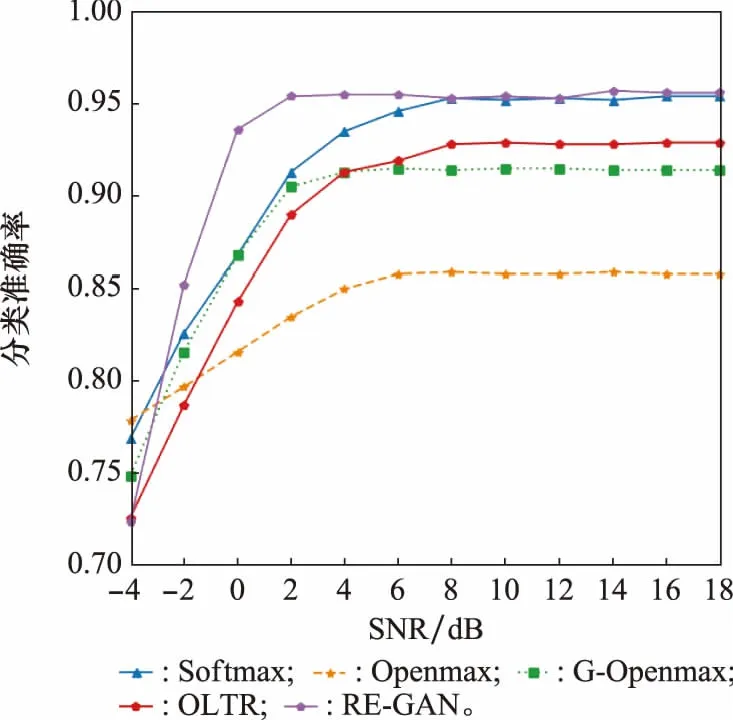
图14 不同算法分类准确率对比Fig.14 Comparison with classification accuracy of different algorithms

表2 不同算法结果对比Table 2 Comparison with results of different algorithms

4 结束语

针对调制信号开集识别问题,本文提出了一种基于RE-GAN的调制信号开集识别算法,该算法区别于传统意义上的闭集识别决策边界,在网络输出层引入激活矢量,通过距离度量和EVT实现对未知调制方式信号的识别。仿真实验结果证明,激活矢量一定程度上可以反映不同类别信号间的差异性;相比较于近年来提出的其他开集识别算法,本文所提算法的网络复杂性低、网络模型更具轻量化,可以更好地对调制信号进行稀疏表达和特征学习,验证了本文算法的有效性。下一步将针对未知类别的信号展开研究,实现对未知类别信号的精准识别。