无人机雷达航迹运动特征提取及组合分类方法

刘 佳, 徐群玉, 陈唯实

(1. 北京航空航天大学前沿科学技术创新研究院, 北京 100191; 2. 中国民航科学技术研究院民航法规与标准化研究所, 北京 100028; 3. 中国民航科学技术研究院机场所, 北京 100028)

0 引 言

无人机技术及产业的快速发展为众多行业应用提供了全新维度上的解决思路[1]。然而,无人机体积小、部署灵活、成本低等优势也为各类非法活动提供了新的作业平台。近年来,多个机场及重点区域频繁出现无人机干扰事件。随着无人机载荷能力以及智能化水平的提升,无人机的潜在安全威胁也在不断增大[2-3]。

为提升安全监管能力,非合作无人机的主动监视以及反制技术近年来成为了研究热点[4]。雷达凭借其监视距离远、全天候工作、全空域扫描等优势成为最适合进行广域范围内无人机监视的技术手段。然而,无人机的雷达目标检测、跟踪与识别也面临众多难题。现有无人机通常采用非金属复合材料制造,体积较小,雷达回波强度低,可识别特征弱,有效检测难度较大[5-6]。小型无人机通常在低空空域内活动,该空域内飞鸟是另一类主要的非合作“低慢小”目标。研究表明,飞鸟和无人机在雷达回波特性(如雷达散射截面)上存在高度相似性[7-10],是无人机目标监视中的主要干扰源,动态环境杂波在满足一定条件时也会形成虚假目标航迹,影响无人机的精确跟踪。

随着雷达目标特性研究的发展,人们发现飞机目标上的活动部件(如螺旋桨)在高速旋转过程中会对雷达回波进行调制;飞鸟扑翼动作产生的非刚性形变也会产生类似的调制效应。采用时频分析算法可以提取该类微多普勒特征[11-12]。实验表明,螺旋桨和扑翼产生的微多普勒特征存在显著差异[13],理论上可用于对飞鸟和无人机进行有效区分[14-16]。然而,在实际复杂环境的监视场景中,微多普勒特征的提取和应用也面临若干问题。现有关于微多普勒特征的提取技术都是基于计算机仿真、暗室测量或者外场理想环境下的近距离测试获取的。在实际环境中,旋翼无人机的微多普勒特征提取效果与雷达驻留时间、测量环境和距离均有密切的关联[17]。因此,现有雷达技术尚难以在较远距离下实现无人机微多普勒特征的快速提取,雷达难以采用监视模式进行观测,限制了其在广域范围内对多个无人机目标的识别与跟踪能力。

雷达对无人机和飞鸟等典型“低慢小”目标通常以航迹的形式进行描述,航迹采样点的时空间信息包含了目标的运动特征。通过对飞鸟和无人机目标航迹进行分析后发现,尽管在飞行速度上接近,但是二者在运动模式上仍然存在显著差异[18]。文献[19]根据航迹运动特征,提出了基于运动模式转换频率的飞鸟和无人机航迹类别判定方法,初步验证了基于航迹运动特征进行“低慢小”目标识别的可行性。本文也采用目标航迹中包含的时空间信息,提出了基于目标航迹的运动特征提取算法,提取了5类航迹运动特征描述子,构建了特征向量,并采用随机森林模型构建分类器,实现了对无人机、飞鸟以及动态降水航迹类别的判定。该识别方法不需要对雷达硬件以及信号处理算法进行改动,具备较强的普适性;由于未采用雷达散射截面以及微多普勒作为识别特征,可以有效地避免雷达定标、环境衰减、微多普勒特征模糊等不利因素的影响,实现雷达在搜索工作模式下对无人机目标的远距离精确识别。

1 飞行机理及行为模式分析

本文提出的无人机目标识别方法主要针对常见的旋翼无人机,因此主要分析旋翼无人机和飞鸟在飞行机理以及行为模式上的特征。

1.1 飞行机理分析

旋翼无人机通过控制不同旋翼的旋转方向和转速来获取升力,并通过调节不同螺旋桨叶片的转速和方向产生升力和拉力偏差,实现机体的上升、下降、前进、旋转、悬停、减速等基本飞行动作,如图1所示。因此,通过对螺旋桨工作模式的智能化调整,无人机具备更高的飞行自由度以及机动能力。气动外形在旋翼无人机设计以及飞行过程中的作用则不像固定翼无人机那样重要。相比之下,飞鸟的飞行动力主要来自于两翼扑动。通过自身姿态的控制结合空气动力学完成机动,大部分情况下飞鸟的运动自由度低于无人机,飞行轨迹相对平滑,短时间内出现大幅度机动的概率较低。飞鸟的飞行机理与气动外形存在密切关联,且仅有极少数鸟类可以实现空中悬停。因此,尽管在飞行速度上类似,两类目标在飞行机理上的本质差异使得飞鸟和无人机都很难完全重现对方的部分飞行模式。图2为无人机目标在航拍、监视等典型作业场景下在水平面维度上呈现出的典型的飞行轨迹。大部分飞鸟则较难呈现出图2中B和D所对应的飞行轨迹。

图1 旋翼无人机和飞鸟飞行机理示意图Fig.1 Schematic diagram of flight mechanics for wing drones and birds

1.2 行为模式分析

从行为模式上看,无人机属于典型的人造目标,其飞行本质上是完成各种指定的作业目的,如监视、侦察、货运、攻击等。因此,无人机的行为模式是驾驶员操作习惯以及作业模式的综合体现。尽管目前无人机正向智能化自主作业方向发展,然而其行为模式本质上仍然是与作业目的和人工智能算法相关联的,存在一定的确定性和预估性。相比之下,飞鸟属于具备自我意识和智能的非人造目标,是典型的非合作目标。飞鸟的行为模式通常与其生活习惯存在密切关联,如迁徙飞鸟和本地留鸟就存在显著差异。同类鸟种之间在做出觅食、返巢、躲避天敌等动作时的飞行机动模式存在差异,而不同鸟种在体型、生活习性以及机动能力上的差异导致其运动模式更加千变万化,对应的目标航迹特征也更具备多样性。

综上所述,在机动能力方面,飞鸟不如旋翼无人机具备更高的自由度,但是鸟类种群自身的多样性及更强的非合作性使其在行为模式上具备更高的复杂度。除了雷达目标特性,飞鸟和无人机在飞行机理以及行为模式上均存在本质差异,而雷达目标航迹中包含的时空间信息则为挖掘并且利用这些差异进行目标识别提供了可能。

2 目标航迹运动特征提取

现有探鸟雷达系统均采用了检测-跟踪-识别一体化的技术体制,因此在探鸟雷达测量数据中,航迹是表征目标最基本的单元。目标航迹是由航迹采样点组成的向量,每个采样点包含时间以及空间信息。由于探鸟雷达扫描速率较大,且飞鸟和无人机飞行速度相对较慢,可近似认为在相邻航迹采样点之间目标为匀速运动,飞行方向为相邻采样点组成的矢量。基于该近似,通过关联航迹中相邻点的时空间信息,结合目标的运动模型可计算出每个航迹采样点的航向、速度等信息。

然而,直接应用航迹采样点的速度和航向信息描述目标运动特征存在一定的局限性:① 目标航迹长度不一致,导致特征向量维度不统一;② 速度和航向分别在时空间维度上描述目标的一阶运动特征,关联性弱,特征描述能力也存在较大不足。鉴于此,需要进一步挖掘航迹中包含的目标运动特征并构建统一维度的特征空间,便于采用机器学习等技术实现对目标的精确识别。本文提出一种基于雷达目标航迹的运动特征提取算法,根据航迹采样点的速度以及航向信息提取了5类运动特征描述子并构建了目标特征向量,并采用随机森林机器学习模型对飞鸟、无人机以及动态降水杂波目标进行识别。3类目标的雷达航迹信息均来自于探鸟雷达系统实际测量数据。飞鸟目标航迹样本来自于雷达对本地留鸟的观测数据并经过人工观测进行交叉验证;无人机航迹样本来自于现场实测;降水在某些情况下会随着风进行运动,在风速和降水强度均满足一定条件的情况下会被雷达误判为飞鸟目标,进而在雷达观测屏幕上呈现出海量的虚假“飞鸟”目标[20]。该类虚假飞鸟目标可以结合气象信息以及人工观测进行判断,但尚无有效的自动化识别手段。

定义某目标航迹为Z=[z1,z2,…,zN],其中zi(i=1,2,…,N)代表航迹的第i个采样点,N为航迹长度。航迹Z对应的速度和航向信息可分别用矢量形式描述为V=[v1,v2,…,vN]和H=[h1,h2,…,hN]。速度信息的单位为m/s。航向信息的单位为(°),定义正北方向为0°,正东方向为90°。基于矢量V和H,本文提取了5类目标运动特征描述子。

2.1 平均速度

平均速度定义为速度矢量V中全部速度信息的统计平均值:

(1)

速度均值描述了航迹的整体平均速度,是目标航迹运动特征最基础的描述子。对于飞鸟和无人机,除悬停模式,大部分情况下两类目标的平均飞行速度较为接近,而降水杂波形成的航迹平均速度则与风速以及雨量大小存在关联,通常情况下速度略慢于飞鸟和无人机。航迹平均速度适用于区分运动特征差异明显的目标,如低空飞鸟以及地面车辆,但是不适用于有效区分飞鸟、无人机及降水杂波航迹,通常可作为一个基础描述子,与其他描述子联合描述目标的运动特征。

2.2 速度标准差

目标航迹不同采样点之间的速度通常存在差异,差异的大小则反映了目标运动特征的不确定性。本文采用速度标准差定量描述目标在速度维度上的变化特征,定义如下:

(2)

标准差越大,表明航迹的速度不确定性越高。飞鸟目标在正常飞行过程中速度变化通常较小,部分情况下飞行轨迹和速度也会呈现一定的高机动和不连续性,但是此种情况出现的概率较低;降水杂波速度特征通常与风一致,对应航迹出现较大速度变化的情况较为罕见;无人机在巡航过程中速度较为均匀,然而在不同作业模式下,其飞行速度的不确定性特征较为复杂,在悬停、转向或者受侧风影响时其飞行速度存在一定的变化。此外,操作人员的操作习惯、熟练程度等因素也会对无人机的飞行速度造成影响。因此,理论上,无人机航迹的速度标准差存在更大的变化范围,具备区分飞鸟和无人机目标的潜力。

2.3 航向偏转标准差

航向信息是通过关联相邻航迹采样点空间位置得到的,与航迹采样点上真正的瞬态航向并非完全一致。然而在足够高的雷达扫描速率下,该航向信息仍可对目标飞行方向进行有效表征。与速度信息不同,航向统计平均值与运动模式无密切关联,而航向偏转产生的角度偏差则可用于描述目标空间位置的不确定性。本文提出航向偏转标准差,对该不确定性进行量化描述,其定义如下:

(3)

结合航向的定义,式(3)中Δh(i)的定义为

(4)

式中:hmean为航迹的平均航向,单位为(°)。在hmean的计算过程中,要考虑到0°和360°之间的关系,从而保障平均航向信息的有效性。δh为航向偏转角度差的阈值,通过对大量航迹相邻采样点的航向角度进行分析,该阈值设定为90°。飞鸟目标的航向偏转程度与其活动模式存在一定关联。通常情况下,本地飞鸟的活动模式较为多样化,飞行航向不确定性大,呈现出的标准差数值变化范围也比较大;迁徙飞鸟的飞行模式确定性相对较高,对应标准差数值略小。无人机目标由于具备空中悬停能力,因而在飞行航向的操作上具备更高的自由度,总体上航迹呈现出的航向不确定性数值跨度较大。此外,无人机飞机航迹与其作业模式密切相关,在作业需要以及环境干扰的情况下,需要进行频繁的姿态修正,因而航迹的空间不确定性以及航向偏转范围也更大。动态降水杂波形成的航迹与风速、风向密切关联,除了短时间的阵风影响,大部分情况下降水杂波航迹的航向偏转程度较低,标准差对应数值较小。

2.4 机动因子

在前3个描述子中,航向偏转标准差描述了航迹采样点的空间不确定性,但没有与时间信息进行关联;速度均值和标准差描述了速度的标量变化特征,而与空间相对位置信息关联度较弱。因此,前3个描述子在各自单一维度上对目标运动特性进行描述。通过对大量目标航迹进行分析后发现,不同类型目标在产生航向偏转过程中呈现出的速度特征是不一样的。高速目标若呈现较大的航向偏转,说明其机动能力较强,反之较弱。该机动能力是对目标在时空间联合维度上运动特征的联合表征。鉴于此,本文提出航迹机动因子,以实现对目标机动能力的量化描述,定义如下:

(5)

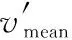
飞鸟的机动特征与鸟种以及活动状态有较大关系。迁徙飞鸟在航迹上体现出来的运动特征较为平稳,通常不会出现明显的高机动飞行。对于本地留鸟而言,觅食、归巢、躲避天敌等动作通常会让飞鸟出现短时间的高机动飞行,该类机动飞行的出现时间以及具体形式存在较高不确定性;对于旋翼无人机而言,由于其具备悬停功能,且飞行机理更类似于直升机,因此理论上运动模式更加多样灵活,机动能力也更加宽泛,且与实际作业目的和场景的关联更加密切。降水杂波的机动特征与风速风向存在密切关联,大部分情况下航迹呈现出的机动特征较弱,仅仅在出现阵风或者风切变等小概率气象特征时虚假航迹会呈现较为明显的机动特征,因此大部分情况下降水杂波形成的虚假目标航迹机动特征较弱,σ值较高。

2.5 震荡因子

机动因子中采用的航向偏转标准差主要描述了航向围绕均值的变化特征,缺乏对航迹中整体航向变化的描述能力。此外,前述4类特征描述子在航迹运动特征描述中也存在一定的局限性。本节以图3所示的两个航迹在水平面上的投影为例对其局限性进行了举例描述,字母A到I描述了雷达航迹的采样点。

图3 常见平滑航迹与典型震荡航迹水平投影示意图Fig.3 Schematic diagram of horizontal projection of regular smooth and typical oscillation tracks

图3(a)描述的航迹较为平滑,运动特征连续,与大部分飞鸟目标航迹相似。图3(b)所示的航迹在实际飞鸟航迹中较为罕见,而无人机做出该类型航迹运动模式难度较低。除了人为刻意操作,无人机在实际作业过程中在进行避障、姿态调整或者遭遇侧风时均有可能做出类似图3(b)所示的震荡。然而,图3中两个航迹的显著差异却无法从前4个描述子中得到体现,原因来自于标准差的计算方法。由于采用了绝对值和平方求和计算方法,标准差仅能描述航向和速度的绝对数值变化,无法体现出航向在顺时针或逆时针方向上的变化。此外,机动因子仅描述了航向相较于平均值的绝对变化,导致航向信息沿着一个方向的连续变化与沿着不同方向的交替变化在统计数值上没有得到充分的体现。因此,前4个描述子无法有效体现出该类震荡航迹的运动特征,目标误判可能性较高。

为解决上述问题,本节提出了震荡因子进行补充描述。该描述子对航迹中每个相邻采样点的特性进行分析,实现了对航迹震荡特性的定量描述。通过计算航迹中每个相邻采样点之间的航向相对差异值τh(k)=hk+1-hk,结合雷达测量误差,计算航迹采样点zk的航向差异符号:

(6)

式中:δe为航向偏转误差阈值,本文定义为0.5°。根据式(6)定义,航向差异符号向量可用矢量描述为O=[1,-1,0,1,…]的形式。根据向量O中相邻元素的正负号变化关系,定义两种震荡模式:①O(i-1)+O(i)=0且O(i-1)≠O(i);②O(i-1)+O(i+1)=0且O(i-1)≠O(i+1),O(i)=0。从航迹的起始点开始进行遍历,若对应符号向量中存在上述两种震荡模式的其中一种,则航迹的震荡次数加1,并记录该次震荡对应的航向角度变化绝对值τh(k)。在遍历航迹全部采样点之后,若航迹中存在K(K>0)次震荡,则计算震荡因子:

(7)

式中:w(k)为加权因子,具体定义如表1所示。震荡次数越多,表明其震荡特征越强。因此,本文定义与震荡次数相关联的加权因子,对单次震荡角度进行加权累加,以实现震荡强度的定量描述,量纲为度。表1定义中震荡次数表示的是第k次震荡,即震荡次数3表示的是航迹发生第3次震荡时采用的权值,因此式(7)所示的累加过程从航迹第1次震荡开始,并随着震荡次数的增加,加权因子根据表1逐渐增大。表1所示加权因子目前基于人工定义,主观性较强,主要体现在震荡次数对于航迹整体震荡强度的影响。在后续工作中,可通过对实验反馈结果的逆向分析,采用拟合的方法对加权因子的数值定义进行进一步优化。

表1 加权因子定义Table 1 Definition of weighting factors

3 监督类机器学习模型

采用本文定义的5类航迹运动特征描述子,可构建目标运动特征空间及特征向量:

S=[vmean,vstd,hstd,σ,ζ]

(8)

根据第2节的定义,式(8)所示特征向量元素之间的物理概念以及量纲是不连续的,包含了目标在不同维度上的本地及全局运动特征。因此,基于式(8),可以保障不同长度航迹的特征向量具备统一的维度,但是需要针对向量中存在的特征不一致性选择合理的分类器。本文选取了随机森林模型构建分类器。随机森林是一种基于多个决策树的组合分类模型,其基本原理是基于可重复随机部分抽样策略构建多重决策树,通过融合多个决策树提供的信息,对目标类别进行综合判定[21]。随机森林模型的基本原理如图4所示。

图4 随机森林基本原理示意图Fig.4 Schematic diagram of random forest fundamental principle

随机森林模型的原理以及实现难度较低。然而,本文需要对选择随机森林模型作为分类器的原因进行进一步的阐述。

(1) 随机森林与其他模型的一个显著区别在于其可对特征空间中的部分特征进行可重复的随机采样并构建不同的决策树分类器。这使得随机森林模型具备更好的抗噪声能力,且过拟合的几率更低[22]。在本文实验中,尽管雷达系统可提供较高精度的目标航迹,然而环境干扰及算法的不确定性使得航迹类别无法保障100%的准确率。因此,训练样本集不可避免地存在质量不确定性,而随机森林的上述特性更加适合该类问题。

(2) 如前所述,特征向量S中的元素之间存在显著的量纲以及物理概念上的不连续性。这种不连续性使得众多常见的机器学习模型(如神经网络、支持向量机等)难以构建高效精确的分类模型,但是并不会对随机森林模型造成显著影响。作为随机森林的基本单元,决策树天然适用于定性和定量问题,且不需要为了特征空间分布构型对描述子进行归一化操作。因此,随机森林模型对于特征描述子的物理概念和量纲连续性敏感度较低,且在加入新的特征元素的条件下可以快速重构森林模型,具备非常好的样本灵活性和适应性。

(3) 随机森林的计算复杂度通常远远小于其他机器学习模型。鉴于飞鸟种群以及运动模式的高复杂性和多样性,无人机识别通常需要根据监视场景条件对飞鸟目标的航迹训练集进行频繁调整。因此,在实际监视场景下,随机森林模型的效率以及样本灵活性具备更加突出的优势。

(4) 随机森林模型中的基尼指数可对特征描述子在分类过程中的重要性进行量化描述[23]。本文介绍的5类特征描述子是根据实际观察与理论分析提出的,针对其实用价值以及各描述子之间的相对重要程度尚无有效的分析及评估方法。基尼指数较好地弥补了这一不足。在第4章的分析中,基尼指数对不同场景下的目标运动特征描述子的重要性进行了量化描述,为进一步认知描述子的合理性以及新特征的挖掘提供了参考依据。

4 实验介绍与结果分析

4.1 实验平台及数据库简介

本研究工作实验数据来自于中国民航科学技术研究院(China Academy of Civil Aviation Science and Technology,CAAC)开发的探鸟雷达系统。探鸟雷达系统示意图如图5所示。该雷达系统采用双天线扫描技术体制,工作频率在S波段。水平扫描天线安装在一个可以调整高度的平台上。发射机采用了峰值功率为0.4 kW的固态功率放大器,机械天线扫描速率为25转/min。系统包含鸟情数据处理与分析软件,具备机场净空区的鸟情探测能力[24-25],对于常见家鸽目标的最大有效观测距离为5 km,采用多目标自动起始与跟踪算法。该雷达系统通过融合水平以及垂直扫描天线的信息实现目标三维坐标(距离、方位、高度)的重构,在3个维度上的分辨率分别为10 m、1°以及5 m。

图5 CAAC探鸟雷达系统Fig.5 Bird surveillance radar systems of CAAC

探鸟雷达系统部署在广西北海福成机场,具体部署位置如图6所示。图6中,区域O和区域P为飞鸟活动较为频繁的区域,也是飞鸟航迹信息的主要数据源。区域Q为无人机实验空域,无人机航迹信息均来自于该实验区域内的无人机飞行。降水杂波信息则来自于机场周边区域。

图6 北海福成机场探鸟雷达系统及实验部署示意图Fig.6 Schematic diagram of bird surveillance radar system and experimental deployment in BeiHai FuCheng airport

实验数据采集时间段为2019年9月3日到10月30日,为最大限度降低无人机对机场空域安全造成的影响,所有无人机飞行实验均安排在深夜或者清晨(没有航班)的情况下进行。飞鸟数据采集时间段集中在7:00到19:00,且选择晴天气象条件较好的条件下进行筛选,通过对比人工观测进行了二次验证,尽可能地保障了飞鸟目标航迹数据的准确性。无人机型号为大疆精灵3系列,在飞行过程中模拟了众多日常应用场景,包括连续航拍,单点图像采集,多点多方位图像信息采集等。通过对比无人机卫星定位航迹和雷达航迹后发现,在无人机悬停超过15 s(6次全空间扫描)之后,现有跟踪算法会丢失目标。在其他机动场景下,雷达系统均可以实现对无人机目标的有效跟踪。根据雷达回波强度,现有探鸟雷达系统将无人机判定为小型飞鸟目标。

通过对雷达航迹与天气情况进行交叉比对后发现,当降水达到中雨级别且随风进行稳定运动时,系统会将降水回波误判为飞鸟目标,回波强度介于小型飞鸟和中型飞鸟目标之间。由于降水杂波通常密度较高且范围较大,因而会形成大量且方向杂乱的航迹,属于典型的环境干扰杂波。降水杂波选取方法基于大量历史数据与气象信息的比对分析,选择了2019年9月中的两个中度降水天气进行动态杂波信息采样,风速大概为10 m/s。降水杂波采样期间,结合视觉观测,仅发现极少数量的飞鸟活动,并且没有进行无人机实验,因此最大程度地保障了采集到的雷达航迹信息均为动态降水杂波形成的虚假目标航迹。

在构建训练以及测试样本集合之前,还需要对原始样本集合进行进一步的优化。结合航迹的多元统计特征,滤除了长度过长或者过短的航迹,静动态杂波引起的多次震荡航迹也通过人工甄别进行了滤除。航迹有效长度定义在4～25之间,震荡次数上限定义为7次。采用随机采样方法构建了不具备重复航迹的训练和测试样本集合。本实验训练数据集中飞鸟、无人机以及降水杂波的航迹样本数量分别为927,635和1 385。测试样本集中3类目标航迹样本数量分别为217,194和239。由于采用不重复随机采样方法,航迹训练样本集和测试样本集的样本重复率为0%。

4.2 实验结果与分析

4.2.1 航迹描述子可分性分析

首先对5类运动特征描述子的有效性在特征空间中进行直观评估。鉴于在五维空间中难以直观描述和观测不同类型目标在特征空间中的可分性,采用主成分分析(principal component analysis, PCA)方法提取出各类目标特征向量中的主成分,并将不同类型目标特征向量的第一和第二主成分投影至二维平面,如图7所示。由图7可以看出,3种类型航迹运动特征存在较为明显的可分性,其中降水杂波与其他两类目标相比,尤其是无人机的运动特征差异尤为明显。由于无人机和降水杂波的动力来源存在本质区别,因此二者之间运动特征的差异可视作无人机与风在运动模式上的差异。飞鸟航迹主成分分布范围较为广泛,与无人机和降水航迹均存在一定程度的重叠。对不同重叠区域的航迹样本特征进行挖掘,有助于进一步认知飞鸟和无人机在运动模式上的差异。与降水航迹重叠明显的飞鸟航迹呈现出较为简单的运动模式,航迹平滑且速度均匀;与无人机高度重叠的飞鸟航迹则呈现出更强的机动能力,其中少量飞鸟航迹甚至呈现出震荡特征,而这类震荡特征则有可能来自于航迹关联算法中的误差。

图7 3类目标航迹特征空间的第1和第2主成分分布Fig.7 Distribution of the first and second principal components in feature space of three types of target tracks

图7中的主成分分布同样呈现出一定的聚类特性。采用k-means算法对聚类中心进行提取后发现,无人机聚类中心附近的航迹有较大比例呈现出类似于图2中B和D航迹的运动模式,这些航迹通常来自于无人机进行空中视频录制或者围绕某特定目标进行多角度图像采集,飞鸟较难呈现出类似的机动能力。综上所述,采用主成分空间投影方法可以较为直观地看出运动特征空间具备有效区分三类目标航迹的可能性。

4.2.2 分类器交叉验证实验

采用随机森林构建分类模型后,本文采用五折交叉验证的方法对分类模型的质量进行评估。表2所示为采用五折交叉验证后的平均识别率模糊矩阵,正确识别率基本达到了85%以上,初步验证了该分类模型的有效性。

表2 三类目标五折交叉验证识别率模糊矩阵Table 2 Fuzzy matrix for recognition rate of five-fold cross validation for three types of targets

在众多监视场景中,降水杂波形成虚假目标航迹的几率较低。因此,分类器区分飞鸟和无人机目标的能力具备更加广泛的应用和研究价值。表3所示为排除降水航迹样本后随机森林分类器五折交叉验证的识别率模糊矩阵。由表3可以看出,飞鸟和无人机正确识别率没有发生明显的变化,总体正确识别率可达85%以上。

表3 飞鸟与无人机目标五折交叉验证识别率模糊矩阵Table 3 Fuzzy matrix for recognition rate of five-fold cross validation for bird and drone targets

4.2.3 目标识别精度及效率评估

表4所示为采用测试样本集之后,分类模型对3类目标的识别率模糊矩阵,与表2所示交叉验证相比,整体识别精度并没有显著下降,仍然达到了85%以上,无人机和降水杂波的误识别率接近0%,表明分类器可以非常精确地区分两类目标,与图7的样本可分性分布特征一致。在剔除降水杂波样本之后,分类器对无人机和飞鸟目标的识别性能没有产生明显变化,如表5所示,这说明飞鸟是无人机目标识别的主要干扰源。此外,根据图6所示,目标航迹样本采集区域距离雷达的平均距离均在1 km以上,因此表4和表5中的实验结果表明本文提出的目标识别方法具备在广域范围内实现无人机目标精确识别的能力。

表4 三类目标识别率模糊矩阵Table 4 Fuzzy matrix of recognition rate for three types of targets

表5 飞鸟和无人机目标识别率模糊矩阵Table 5 Fuzzy matrix of recognition rate for bird and drone targets

为了对本文提出方法的性能进行横向验证,采用文献[19]介绍的方法对本文构建的航迹样本库进行目标分类。由于文献[19]方法仅能对无人机和飞鸟航迹进行二分分类,因此数据库中去除了动态降水杂波航迹。表6所示为两类方法对飞鸟和无人机目标的正确识别率。从表6可以看出,本文所提方法在识别性能上要略好于文献[19]提出的方法。通过对文献[19]中的误判断样本进行分析后发现,造成该方法误判的主要原因在于文献[19]假设飞鸟目标机动性高于无人机,因此对于高机动无人机航迹以及平缓飞鸟航迹的类别进行了误判,降低了整体正确识别率。

表6 本文与文献[19]分类方法对飞鸟和无人机目标的正确识别率比对Table 6 Comparison of the correct recognition rate of bird and drone targets using classification methods in this article and [19]

与无人机这类人造目标不同,飞鸟以及降水杂波的运动特性与环境存在密切关联,因而即便是在同一个监视场景下,不同季节和不同时段的飞鸟以及降水杂波也会呈现出较大的运动特征差异。这就使得目标识别系统需要频繁地更新调整训练样本数据集,以实现对目标运动特征的准确描述,也对分类模型的样本鲁棒性提出了较大挑战。为了进一步验证随机森林模型的样本鲁棒性,本节将既有训练和测试样本集融合为一个新的训练集。基于新的训练集构建随机森林分类模型后,进行了五折交叉验证实验,分类模糊矩阵如表7所示。与表4进行比对后可以看出,3类目标的正确识别率没有发生明显的变化,说明训练集的变化并没有对分类器性能造成显著影响,分类模型具备较好的样本鲁棒性,适用于需要频繁调整训练样本的目标识别场景。需要说明的是,本节实验仅部分反映了分类模型鲁棒性,受限于实验数据样本,尚无法进行更加充分的验证。

表7 基于新融合训练集的五折交叉验证模糊矩阵Table 7 Fuzzy matrix of five-fold cross validation based on new fusion training set

在识别效率方面,由于随机森林模型的复杂度以及特征向量维度较低[26],在训练以及识别过程中均不会过度消耗计算机资源。本实验采用的随机森林模型基于python平台开发,计算机采用Intel i5-7500中央处理器,内存为16 GB。由于训练集数量较小且维度低,构建随机森林模型的平均训练时间仅为17.6 s,单一未知航迹特征向量类别判定的平均时间为0.31 s,几乎可以实现未知目标的准实时识别。基于上述对分类模型的识别精度、样本鲁棒性以及识别效率的分析可以看出,由目标航迹运动特征和随机森林模型构成的目标识别系统具备较好的工程应用价值。

4.2.4 基于基尼指数的特征重要性评估

图8采用基尼指数对描述子重要性进行了评估,基尼指数越大,对应特征描述子在分类中的重要性越高[27]。机动因子对应最大基尼指数表明,在识别无人机、飞鸟和降水杂波3类目标的过程中,目标机动能力是区分3类目标的主要依据。基尼指数最小的平均速度则表明其在分类过程中的重要性最低,与理论分析和经验预期一致。在去除降水杂波航迹后。目标识别过程中的基尼指数分布如图9所示,其中机动因子在识别飞鸟和无人机的过程中仍然是最重要的区分特征。图8和图9的主要区别在于航向偏转标准差重要性的显著下降。一方面,表明在区分降水杂波与另外两类目标过程中航向偏转标准差起到了非常重要的作用;另一方面,由于飞鸟和无人机在连续航迹内均可以做出较大的航向变化,但是变化的方式以及航迹采样点时空间关系存在显著差异,而这类差异在航向偏转标准差中难以体现出来,从而导致航向偏转标准差在区分两类目标过程中的贡献程度出现了较大的下降。相比之下,航向偏转标准差体现出来的不足则由震荡因子进行了补充描述,其重要性的进一步提升则表明其在描述飞鸟和无人机目标运动特征差异性上的有效性。

图8 随机森林模型基尼指数分布-三类目标识别Fig.8 Random forest model Gini exponential distribution- three types of target recognition

图9 随机森林模型基尼指数分布-飞鸟无人机目标识别Fig.9 Random forest model Gini exponential distribution- bird and drone target recognition

上述分析表明,基尼指数对特征描述子重要性的定量描述与人工观测的直观分析较为一致,该指数有助于进一步加深对目标运动特征的认知,为探索新的目标可识别特征提供参考。

4.2.5 现有工作存在的不足

现有实验结果对本文提出的特征提取与目标识别方法进行了验证。然而,现有工作仍然存在改进的空间,主要体现在以下几个方面。

(1) 本文提出的特征提取技术基于目标跟踪航迹,因此与跟踪精度存在密切关联。通过对现有观测数据进行分析后发现,雷达系统在跟踪大群飞鸟的过程中,关联算法中存在的不确定性会产生部分非正常航迹。该类航迹通常呈现出一定的震荡特征,易造成目标类别的误判。在后续工作中,除了进一步优化跟踪关联算法,还需要实现系统对空中集群目标的智能判定以及跟踪[28]。

(2) 本文提出的目标识别算法并没有考虑雷达回波特征,如雷达散射截面,这使得该方法不受雷达定标以及数据安全的影响,可以广泛应用于各类型探鸟雷达监视系统。然而,若可以将雷达散射截面等雷达目标特性与航迹运动特征融合,挖掘其综合目标特性,则有助于进一步丰富目标的可识别特征,提高目标的正确识别率。这也将是本研究后续的主要工作方向之一。

(3) 通过对误分类样本进行分析后发现,对于运动模式较为简单且平滑的飞鸟和无人机航迹,现有识别方法仍然难以进行完全有效的区分。该类航迹在运动模式以及雷达回波上均呈现出高度相似性。为进一步提升识别性能,需要引入其他信息进行辅助决策。对现有飞鸟观测数据进行分析后发现,飞鸟的活动特征、地理位置以及时间均存在密切关联,因此可结合雷达观测区域内的地理以及时间信息,建立飞鸟活动的联合概率密度模型,辅助系统对特定时间及区域内出现的目标航迹类别进行判定。该方法与认知雷达理论关联密切[29-30],也是今后基于探鸟雷达系统进行鸟情信息挖掘以及环境认知的主要研究方向之一。

5 结 论

本文分析了飞鸟和无人机在飞行机理和行为模式上的差异,提出了基于航迹时空间信息的目标运动特征提取方法,构建了特征空间。基于探鸟雷达系统提供的无人机、飞鸟和动态降水杂波的航迹信息,结合运动特征向量构建了随机森林分类模型,得出以下结论:

(1) 无人机的平均正确识别率可以达到85%以上,可实现无人机的高精度识别;

(2) 随机森林模型计算效率较高,可实现准实时目标识别,且该模型具备较好的样本鲁棒性;

(3) 基尼指数清晰描述了目标识别过程中运动特征描述子的重要性,为深入了解目标运动特征以及新描述子的挖掘提供了参考;

(4) 本文提出的无人机目标识别方法尚有改进空间,多尺度集群目标跟踪、雷达回波特征融合以及基于认知雷达理论的辅助决策,将是今后进一步研究的主要方向。