基于稀疏贝叶斯学习的稳健STAP算法
李仲悦, 王 彤
(西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071)
0 引 言
空时自适应处理(space-time adaptive processing, STAP)能够联合空时两维自由度,在二维联合域形成与空时耦合杂波相匹配的斜凹口,有效提升机载雷达杂波抑制和目标检测性能[1-3]。当用于杂波加噪声协方差矩阵(clutter-plus-noise covariance matrix, CCM)估计的独立同分布(independent and identically distributed, IID)样本数大于系统自由度2倍时,STAP算法可以获得较为理想的处理性能。然而受阵列非理想配置以及观测场景快速变化的影响,机载雷达的实际工作环境都是非均匀的,通常难以获得期望的IID样本数,进而导致STAP算法性能下降。
针对上述问题,国内外科研工作者进行了积极的探索,取得了丰富的研究成果。文献[4]利用杂波的低秩特性将样本需求数减小到杂波秩的2倍。文献[5]通过二维谱变换增加非正侧阵样本的利用率。文献[6]通过非均匀检测器剔除统计特性不一致的样本。文献[7]利用先验的环境信息提高CCM估计性能。文献[8]利用滑窗技术实现基于单快拍的目标检测。上述算法虽然可以提高非均匀环境下的杂波抑制性能,但对雷达工作模式、天线阵列结构以及先验信息配准精度提出了较高的要求,所以在实际应用中存在较多限制。
近年来,随着稀疏恢复(sparse recovery, SR)理论的快速发展,研究人员提出一种基于杂波内在稀疏性的SR-STAP方法[9-11]。由文献[9-11]的理论和仿真分析可知,SR-STAP算法利用少数几个甚至一个观测数据就可以获得高精度的CCM估计,为提升非均匀环境下杂波抑制性能提供了一种新的途径。SR-STAP算法一般包含两个步骤:一是离散化空时平面并构建稀疏信号模型;二是求解上述信号模型中的稀疏参数并利用其计算CCM。已有的SR-STAP文献通常假设杂波数据能够由离散化的字典矩阵精确表示。但在实际应用中,离散化处理以及阵列幅相误差的存在会导致接收数据与稀疏信号模型的失配,进而降低SR-STAP算法的CCM估计精度。
为了减小模型失配造成的影响,文献[12-16]对离散化处理造成的格点失配现象进行了分析,提出局域化搜索和非均匀划分的空时字典校准算法;文献[17-18]对由阵元幅相误差造成的失配现象进行了分析,提出误差参数和角度-多普勒像交替迭代的算法。但是,文献[12-18]仅考虑了由单一失配导致SR-STAP算法性能下降的问题,对于两种失配同时存在的情况还需进一步探索。
针对上述问题,本文提出一种基于稀疏贝叶斯框架[19-20]的稳健STAP (robust sparse Bayesian learning-based STAP,RSBL-STAP)算法。RSBL-STAP算法首先利用导向矢量的Kronecker结构构建阵列幅相误差和格点失配同时存在情况下的误差信号模型,然后利用贝叶斯推断和最大期望(expectation maximization,EM)算法[21-25]迭代求取角度-多普勒像、阵列误差参数以及格点失配参数,最后利用求解参数计算精确的CCM和STAP权矢量。此外,为了减小模型构建所增加的计算复杂度,本文还提出了一种基于空域通道的自适应降维字典矩阵设计方法。仿真实验证明了所提算法的正确性与有效性。
本文所提算法主要贡献可归纳如下:
(1) 构建阵列幅相误差和格点失配同时存在情况下的SR-STAP误差信号模型;
(2) 推导稀疏贝叶斯学习(sparse Bayesian Learning, SBL)框架下误差参数的迭代求解过程;
(3) 提出一种基于空域通道的自适应降维字典矩阵设计方法。
1 信号模型
考虑一个机载脉冲多普勒雷达系统,天线是由N个阵元构成的均匀等距线阵,阵元间隔为半波长(d=λ/2)。假设雷达发射机在一个相干脉冲处理时间内发射M个脉冲,脉冲重复频率(pulse repetition frequency, PRF)为fr,则理想接收信号[2]可以表示为
(1)

(2)
式中:fd,k和fs,k分别表示第k个杂波块的归一化多普勒频率和归一化空间频率。然而在实际应用中,受工艺技术水平以及工作环境等因素影响,天线阵元间的一致性会被破坏,也就产生了所谓的“阵元幅相误差”,进而导致接收信号与理想信号模型的失配。
假设se=[se,1,se,2,…,se,N]T为阵列幅相误差矢量,将其引入式(1),则实际接收信号模型[17-18]可以修正为
(3)

假设各分量之间相互独立,则根据式(3),可将接收数据的理想CCM表示为
(4)
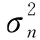
但是在实际应用中,难以精确获取观测场景中杂波实际分布信息。为了解决上述问题,SR-STAP算法利用杂波在角度-多普勒平面上的稀疏性,将连续的二维平面均匀离散划分为Ns个空域通道和Nd个时域通道。令v(fd,j,fs,i)(j=1,2,…,Nd,i=1,2,…,Ns)表示空时离散通道相交格点上的导向矢量,如果集合V={v(fd,1,fs,1),v(fd,2,fs,2),…,v(fd,Nd,fs,Ns)}包含式(3)中Nc个杂波块的空时导向矢量,则式(3)可以进一步表示为
(5)

(6)

(7)
式中:αs=[αs,1,αs,2,…,αs,Ns]T表示辅助原子对应的稀疏系数。经过简单的矩阵变换[21-22],式(7)可以重新表示为
(8)
式中:
(9)

(10)
在多快拍下可以扩展为
(11)
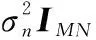
(12)
2 RSBL-STAP算法
本节推导基于SBL框架的RSBL-STAP算法。为了促进角度-多普勒像的稀疏性,本文假设稀疏系数矩阵A服从广义双重帕累托(generalized double Pareto,GDP)先验分布[23]。根据文献[23],A的GDP分布可以利用以下3层先验假设得到:首先,假设参数A各列具有联合稀疏性且服从均值为0、方差为Γ的复高斯分布,即
(13)
式中:Γ=diag(γ);γ=[γ1,γ2,…,γQ]T;Q=Ns(Nd+1)表示离散格点上的杂波功率。然后,假设超参数γq彼此独立且服从参数为βq的Gamma分布,即
(14)

(15)
式中:h是一个小的正常数。
(16)
式中:fd,t和fs,t分别表示目标的归一化多普勒频率和空间频率。
(17)

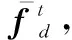
(18)

(19)
问题1和问题2的具体求解步骤分别由第2.1节和第2.2节给出。
2.1 问题1求解
本节利用EM算法对问题1进行求解,EM算法包含两个计算步骤。


(20)

(21)
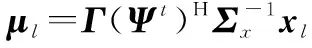

步骤 2.1更新超参数γ,β。超参数(γ,β)的似然函数[19-25]可以表示为
L(γ,β)=E{Inp(A|γ)p(γ|β)p(β)}∝
(22)
式中:μl,q表示μl的第q个元素;Σq,q表示矩阵Σ的第(q,q)个元素。计算式(22)关于参数γq的偏导数,即
(23)
令式(23)为0,即可得到参数γq的更新公式[23]为
(24)
同理,可得超参数βq的估计值为
(25)
步骤 2.2更新误差参数se。误差变量参数se的似然数L(se)可以表示[21-22]为
(26)
式(26)中关于参数se的偏导数可以表示为
(27)
式中:
(28)
令∂L(se,εe)/∂se=0,得到se的更新表达式
(29)
式中:
(30)

(31)

(32)
2.2 问题2求解
在推导相关函数之前,先对将要用到的变量符号做如下定义[15,23,25]。


(33)
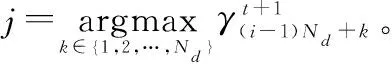

利用各参数间的独立性计算超参数γ的边缘似然函数,即
(34)

(35)
令
(36)

(37)

(38)
其中,
(39)

(40)

(41)
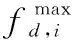
(42)
(43)

3 降维字典矩阵设计
不同于传统的SR-STAP算法,本文所提RSBL-STAP算法为了分离误差变量,在模型构建时进行了字典矩阵对角化操作,导致字典矩阵维度的增加以及计算效率的降低。针对上述问题,本节在文献[26]的基础上利用角度-多普勒像的稀疏性设计了一种基于空域通道的自适应降维字典矩阵,具体设计过程如下。

(44)
式中:vsub(fd,k,fs,i)表示子孔径导向矢量。
步骤 2定义Pi=[P(fd,1,fs,i),P(fd,2,fs,i),…,P(fd,Nd,fs,i)](i=1,2,…,Ns)表示第i个空域通道内离散化格点对应的估计值,则第i个空域通道的选取门限Thi可以表示为[26]
(45)
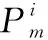

4 仿真验证
本节通过仿真实验对所提算法的有效性进行验证。仿真实验中阵列幅相误差设置为5%,其他系统仿真参数如表1所示。

表1 雷达系统仿真参数Table 1 Simulation parameters of radar system
此外,仿真实验中问题1的最大迭代次数和停止参数分别设置为103和10-12;问题2的格点搜索参数和精细划分格点数分别设置为υ=1.12和P=11;RSBL-STAP的迭代停止条件设置为迭代次数t≥8或者格点搜索间隔Δf≤0.008;空时离散化格点数为Nd=Ns=6N;样本数为L=10。
下面从Capon谱估计能力、自适应方向图形成能力、输出SCNR损失性能、目标检测性能以及计算时间5个方面对所提算法性能进行评估验证。
实验 1Capon谱估计性能
由于CCM估计精度决定了STAP算法的性能,所以本实验利用Capon谱对所提算法的杂波统计特性估计能力进行评估,并与最优(optimum, OPT)算法[2]、SBC-STAP算法[11]以及网格失配自校正SBL-STAP(off-grid self-calibration SBL-STAP, OS-SBL-STAP)算法[15]等算法进行了对比分析,结果如图1所示。

图1 不同算法的Capon谱Fig.1 Capon spectra of different algorithms
从图1可以看出,幅相误差和格点失配会导致传统SBL-STAP算法所估计的Capon谱发生展宽并在杂波清晰区产生大量功率较强的扰动信号。OS-SBL-STAP算法通过增加格点搜索步骤可以在一定程度上减小Capon谱展宽程度,但是受限于最小二乘估计精度以及幅相误差影响,其谱估计能力依然有限。本文所提算法同时考虑率了两种误差,在利用GDP先验分布提高待估参数稀疏性的同时还获取了误差参数的高精度估计,所以能够获得与OPT-STAP接近的Capon谱估计性能。
实验 2自适应方向图形成能力
为了对杂波抑制性能进行更详细的对比分析,图2给出了各算法的空时二维自适应方向图,其中目标假设位于阵列主瓣指向,相应多普勒频率设置为0.299。从图2可以看出,由于所提RSBL-STAP算法补偿了阵元幅相误差和格点失配的影响,所以能够与OPT-STAP算法一样,在于目标指向处形成最大增益的同时在杂波分布区域形成窄且深的凹口。相反地,由于无法彻底消除阵元幅相误差和格点失配的影响,OS-SBL-STAP以及传统SBL-STAP的波束指向与真实目标方向会有一定的偏差,所形成的杂波凹口也有一定程度的展宽。

图2 二维自适应方向图Fig.2 Two-dimensional adaptive patterns
为了更好地对比各算法的凹口形成能力,图3和图4分别给出了目标所在时、空通道的方向图切片以及局部放大图,从中可以看出在阵列幅相误差影响下,传统SBL-STAP和OS-SBL-STAP算法所估计的滤波器权矢量不能对准目标指向,这会带来目标相干积累损失。此外,相较于所提算法,上述两种STAP算法的凹口形成能力也有不同程度的恶化,这是因为阵列幅相误差和格点失配的存在会导致杂波能量不能被真实估计,而是分散于周围格点上,因此会造成STAP权矢量凹口展宽,深度减小,最终导致算法杂波抑制性能下降。

图3 时域自适应方向图Fig.3 Adaptive pattern in temporal domain

图4 空域自适应方向图Fig.4 Adaptive pattern in spatial domain
实验 3输出信杂噪比(signal to clutter plus noise ratio,SCNR)损失性能
为了更清楚地反映各算法的杂波抑制性能,图5给出了各算法SCNR损失随多普勒频率变化的曲线,其中SCNR损失定义为各算法输出SCNR与噪声环境下匹配滤波器输出信噪比(signal to noise ratio, SNR)的比值[2],即

图5 SCNR损失对比图Fig.5 Comparison diagram of SCNR loss
(46)
式中:w表示估计的滤波器权矢量;R表示误差环境下真实的CCM。
从图5可以看出,幅相误差和格点失配导致的谱展宽和清晰区扰动会降低SBL-STAP和OS-SBL-STAP算法输出SCNR。而所提算法利用重构的误差信号模型和迭代算法消除了相关影响,所以能够获得近似OPT-STAP的性能。此外,图5还给出了直接数据域STAP (direct data domain-STAP, DDD-STAP)算法,迭代自适应STAP (iterative adaptive approach, IAA-STAP)算法以及对角加载STAP (loading sample matrix inversion STAP, LSMI-STAP)算法的输出SCNR损失曲线。从图5可以看出IAA-STAP与SBL-STAP以及OS-SBL-STAP算法一致,在模型失配存在时其输出SCNR损失性能相较于OPT-STAP而言有较大程度的下降。受自由度损失和阵列幅相误差双重影响,DDD-STAP算法在旁瓣杂波区域的输出SCNR损失性能则要略逊一筹。但是在主瓣杂波区域,DDD-STAP算法性能则要优于SBL-STAP算法、OS-SBL-STAP算法以及IAA-STAP算法,这是因为利用滑窗技术的DDD-STAP算法在获得更多训练样本的同时避免了传统SR-STAP算法格点失配带来的性能损失,所以在主瓣杂波区域具有较好的输出SCNR性能。此外,虽然利用稀疏恢复技术的SBL-STAP算法、OS-SBL-STAP算法以及IAA-STAP算法在信号模型失配时性能损失严重,但是在小样本环境下相较于传统的LSMI-STAP算法仍具有较大的优势。
实验 4目标检测性能
本实验利用检测概率Pd评估所提算法的目标检测性能,其中虚警概率Pfa设置为10-3。图6给出了各算法检测性能随目标SNR变化的结果,其中图6(a)~图6(c)分别假设目标归一化多普勒频率为0.5、0.2以及0.008,主要反映各算法对快速、中速以及慢速运动目标的检测性能。

图6 检测概率曲线Fig.6 Curves of detection probability
从图6可以看出,与其他SR-STAP算法相比,本文所提算法对不同运动速度和SNR的目标都具有近似最优的检测性能。这是因为所提算法能够正确补偿模型失配对稀疏角度-多普勒像以及目标导向矢量的影响,在保证滤波器权矢量指向目标的同时,在杂波区域形成窄且深的凹口,最终获得近似最优的目标检测性能。
实验 5计算时间
最后,对所提算法的计算效率进行评估。图7给出了不同SR-STAP算法计算时间随阵元数目变化的示意图(脉冲数与阵元数一致,仿真实验由标准台式计算机完成,计算机中央处理单元为Intel Xeon E5-2620@2.10 GHz×2)。从图7可以看出RSBL-STAP算法、OS-SBL-STAP算法以及SBL-STAP算法的计算时间要大于IAA-STAP算法,这是因为基于SBL框架的STAP算法需要计算稀疏系数的协方差矩阵以及逆矩阵,而IAA-STAP算法仅需要计算接收数据的协方差矩阵和逆矩阵,由于稀疏系数维数远大于接收数据自由度,所以基于SBL框架的STAP算法具有更高的计算复杂度。此外,由于误差信号模型在构建过程中的对角化操作,本文所提RSBL-STAP算法的计算时间要大于OS-SBL-STAP算法以及SBL-STAP算法。
5 结 论
针对误差环境导致传统SR-STAP算法性能下降的问题,本文提出一种基于SBL的稳健SR-STAP算法。该算法首先利用空时导向矢量的Kronecker结构构建SR-STAP误差信号模型,然后利用贝叶斯推断和最大期望算法迭代求取各参数,并计算CCM和STAP权矢量。仿真结果表明,所提算法能够消除阵列幅相误差和格点失配对杂波统计特性和目标导向矢量估计的影响,在目标指向形成最大增益的同时还能在杂波分布区域形成窄凹口,显著提高了误差环境下非均匀杂波抑制和目标检测性能。但是,相较于其他SR-STAP算法,本文所提算法在误差信号模型构建过程中的对角化操作会增加算法的计算复杂度,因此在算法模型优化和实时性方面还需要进行更进一步的研究。

