基于DSGD的分布式电磁目标识别

王宏安, 黄 达, 张 伟,*, 潘 晔, 王祥丰, 邵怀宗, 顾 杰

(1. 电子科技大学信息与通信工程学院, 四川 成都 611731; 2. 电子信息控制重点实验室,四川 成都 610036; 3. 华东师范大学计算机科学与技术学院, 上海 200062)

0 引 言

电磁目标识别根据通信侦察设备侦测到的目标通信信号参数,识别、确定通信目标的类别、种类和属性。该技术在民事领域已被广泛应用于频谱管理、干扰识别以及认知无线电等。而在军事领域,它可提供全面、完善的战场目标信息,有助于作战人员及时掌握战场态势、减少友军误伤。

目前针对电磁目标识别的机器学习方法多是在集中式场景下进行的。针对分布式场景下的电磁目标识别的研究较少。然而随着军民用电磁装备的数量、类型以及更新速度快速增长,自适应对抗技术飞速发展以及电磁系统数字化程度越来越高,电磁环境呈现出高度复杂化、动态化的特征。这造成采集信号数据量剧增(达TB、PB甚至EB级),庞大的数据存储和计算在单机上是远远做不到的,且硬件支持的有限性使得在单机上进行大数据处理十分吃力,将计算模型或者数据分布式地部署到多台、多类型机器上,分别在不同的计算节点上学习,能够在硬件上实现水平拓展,突破设备硬件限制,提高数据计算的速度和可扩展性,减少任务的耗时。

本文结合电磁目标识别技术及分布式最优化理论,提出了一种基于去中心化随机梯度下降(decentralized stochastic gradient descent, DSGD)[1]的电磁目标识别方法。并在手机电磁数据上进行了实验验证,将数据分布到多个节点中,通过相邻节点间传递梯度,然后使用去中心化随机梯度下降的方法更新本地节点模型。同时,将所提方法与集中式场景的单机训练进行了对比,验证了该方法的有效性。

1 相关工作

1.1 电磁目标识别

电磁信号识别是从源电磁信号样本中识别出对应样本类别,从而完成相应的识别任务。早期,对电磁信号识别任务使用的是采用信号处理方式直接进行识别[2]。但随着现代社会和战场上电磁信号数量的急剧增加,信号密度呈指数级增长,信号形式日趋复杂。传统电磁目标识别方法难以快速有效应对日益复杂的电磁环境,结合机器学习方法进行电磁目标识别逐渐成为趋势。Wang等[3]运用将复值神经网络和网络压缩相结合的方法,既提高了识别性能,又降低了模型复杂度和尺寸。Zhang等[4]利用动态曲线拟合和反向传播神经网络组成的反馈分类算法,根据信号指纹特征实现了移动电磁目标的无监督识别。文献[5]通过在时域和频域注意机制中使用一种新颖的复数傅里叶神经算子块,可以从不同领域充分学习特征。Wan等[6]利用信号的双谱和模糊函数作为特征,通过深度学习网络对特征进行识别,提高了电磁目标识别的性能。Qu等[7]提出一种多域特征融合与集成学习相结合的方法,提高了标记样本较少的通信辐射源的识别。Hou等[8]提出一种辐射源二维双谱与卷积神经网络(convolutional neural network, CNN)相结合的方法。相比其他结合双谱特征的算法,该方法在精度和复杂度上都有优势。文献[9]利用孪生网络来解决电磁目标跨模式识别的问题,相较于传统CNN,效果提升了20%。蒋季宏等[10]运用不同信号分析处理方法得到的特征进行拼接融合,实现了电磁信号的小样本识别。文献[11]利用电磁信号的特性,设计了一种基于高阶累积量的树形干扰识别分类器,该分类器具有极高的识别率。文献[12]将决策树与Ada Boost结合用于雷达电磁信号识别,较好地解决了高密度信号环境下传统电磁信号识别实时性差、识别精度低的问题。文献[13]将雷达电磁信号转化为符号序列,提取多尺度信息熵作为识别特征,利用K最邻近法(K-nearest neighbor, KNN)进行分类识别,具有良好的抗噪性。张思成等[14]将电磁信号具象化为二维图像,在保证识别率的同时极大地减少了模型参数计算的规模。

1.2 分布式最优化与分布式计算

分布式电磁目标识别计算框架旨在利用分布式最优化或分布式机器学习方法来分布式地实现传统电磁目标识别。分布式最优化方法是指在由多个计算节点构建的网络中进行机器学习或者深度学习,其目的为实现更大规模的训练数据和模型,加快训练效率。目前分布式最优化方法已在智能电网[15]、信息物理融合系统[16]、无人驾驶飞行器系统[17]等很多领域得到应用,但是针对电磁目标识别场景下的分布式研究应用较少。

以下介绍常用的基于分布式最优化或分布式计算的方法。

All-Reduce[18]:该方法在每次迭代过程中,从节点将计算的参数传递给主节点,经主节点对所有节点传递过来的参数进行处理后,再将其传给每个从节点,更新从节点参数,实现参数一致性,达到加速训练的效果。文献[19]证明了算法的可行性,文献[20-21]使用该方法实现了分布式平台以及集群环境。

Ring-AllReduce:该算法将N个节点分布在一个环上,并将每个节点的数据分成N份。在每个循环过程中,当前节点会收到上一个节点传过来的数据,在此循环下,最终每个节点都会包含最终结果的一份,达到一致性。该方法也在文献[22]中用于解决图形处理器(graphic processing unit, GPU)之间的高效通讯。

横向联邦学习[23]:主节点将初始模型分发给从节点,然后从节点根据本地数据集分别对模型进行训练,将训练后的模型加密后传至主节点,在主节点将所有模型梯度聚合后再将其加密传回各从节点。

交替方向乘子法(alternating direction method of multipliers,ADMM)[24-26]:该方法适用于大规模的分布式优化问题的分布式求解。为了处理约束,该方法结合增广拉格朗日乘子法与Gauss-Seidel计算技巧,实现分布式最优化问题的迭代求解。该方法在网络通信[27-28]等领域分布式场景中得到广泛应用。

尽管国内外研究人员取得了大量的研究成果。例如随着电磁环境日趋复杂,针对传统基于信号处理的方法难以实现快速准确识别的问题,不少研究人员将机器学习的方法应用于其中以解决该问题,但都是在小样本或者数据量规模较小的场景下,使用集中式机器学习或者深度学习方法进行识别。结合分布式机器学习进行电磁目标识别的研究还较少。对于大数据背景下的电磁目标识别,分布式机器学习在识别效率高、设备计算及存储能力要求低等方面有着独特优势,将分布式机器学习用于电磁目标识别有着很好的应用前景。

2 理论基础

2.1 短时傅里叶变换

傅里叶变换常用于平稳信号的处理,且只能反映出信号的频域特性。在现实世界中,需要分析和处理的信号往往是时变的或是非平稳的,其统计量,如相关函数,功率谱等也都是时变函数。在这种情况下,希望得到信号频谱随时间的变化,故Gabor于1946年提出了短时傅里叶变换(short-time Fourier transform,STFT),其实质是加窗的傅里叶变换。通过窗函数的不断移动,得到整段信号的频谱随时间的变化,其计算公式如下:

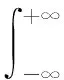
(1)

式中:x(t)为原始信号;h(t-τ)为窗函数,τ表示窗函数移动的位置;F(t,f)为STFT变换后的结果。可以看出,STFT就是先将信号x(t)乘以窗函数h(t-τ)的共轭,再做傅里叶变换。

窗函数每移动一次,就会得到一个复数值。在窗函数移动到信号尾端时,表示处理结束,最终得到一个维度为n×m的复数矩阵。其中,n与窗函数h(t-τ)移动的次数有关,m与窗函数的宽度有关。

2.2 神经网络介绍

目前的神经网络架构主要有3种,基于卷积池化的残差网络(residual network, ResNet)[29]、基于多层感知机制(multi-layer perceptron, MLP)的MLP-mixer[30]和基于注意力机制的Transformer[31]。本文选用前两者分别作为训练网络,以探究不同网络架构在分布电磁目标识别中影响。

2.2.1 ResNet

ResNet通过引入残差连接,很好地解决了由于神经网络加深而引起的网络退化问题。用ResNet101作为训练网络,ResNet101由33个模块加上一些单独的卷积层(Conv)、池化层和全连接层组成,其网络结构如图1所示。

图1 残差网络101Fig.1 ResNet101

2.2.2 MLP-mixer

MLP-mixer是一种完全基于MLP的网络结构。在将输入数据分为多个patch后,输入进一个全连接层,再经过多个混合层后,进行全局平均池化,最后再经过一个全连接层后输出类别。其中,每个混合层使用了两种类型的MLP层、通道混合层和位置混合层。通道混合层通信不同通道上的信息,位置混合层通信不同空间位置上的信息。MLP-mixer的网络结构如图2所示。

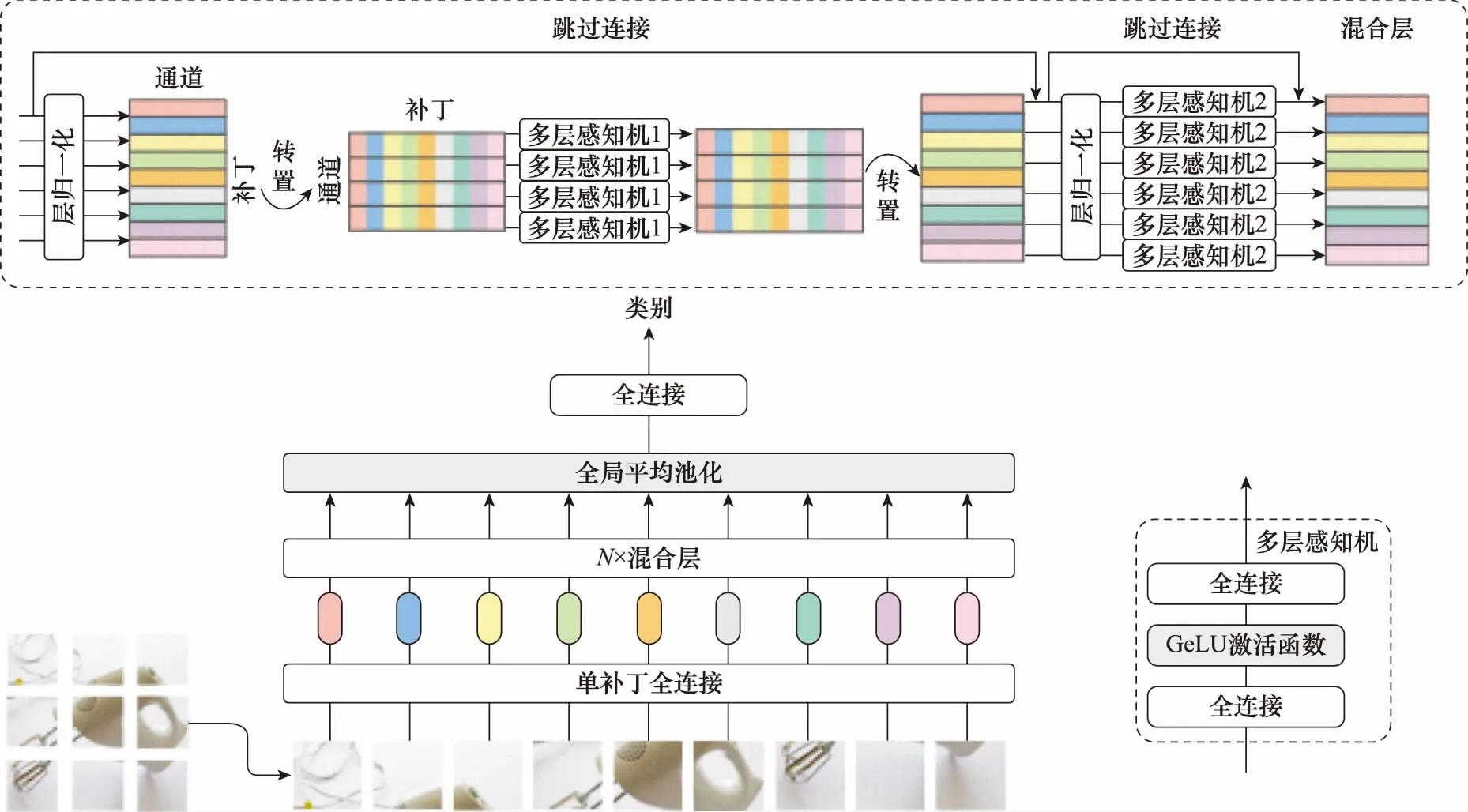
图2 MLP-mixerFig.2 MLP-mixer

2.3 分布式架构

对于分布式系统架构,其网络拓扑结构的决定因素是系统设计实现的分布程度。根据具体场景不同,分布式系统的拓扑结构可以设计为星型拓扑、树型拓扑及点对点型拓扑。分布式拓扑结构示意图分别如图3(a)～图3(c)所示。其中,星型拓扑(见图3(a))采用严格的分层方法进行聚合,聚合发生在单个中心位置;树型拓扑(见图3(b))允许中间的节点进行聚合操作,通过每层之间数据信息的计算与传递完成分布式感知任务。由于每个节点只需与其父节点和子节点通信,所以树状拓扑具有易于扩展和管理的优点;点对点型拓扑(见图3(c))中的每一个节点都相对独立,系统没有为某些节点分配特定的任务,每个节点都拥有完整的信息,并且可以与任何其他节点进行通信。点对点型的拓扑结构比前两种拓扑结构具有更高的可伸缩性和鲁棒性,不容易因单个节点被影响而影响到整个系统。但相应地,系统的通信量也会很大,需要根据实际情况来设计满足场景需要的分布式拓扑结构。由于本文针对的是去中心场景,所以采用点对点型的拓扑结构。

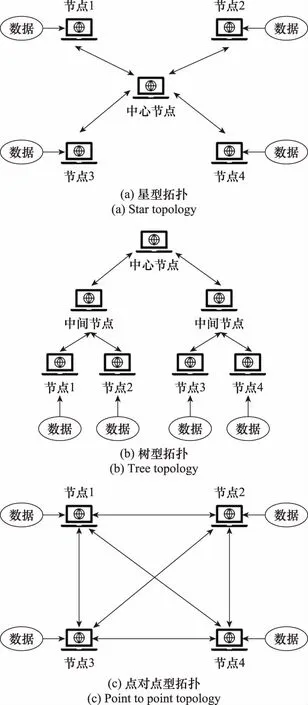
图3 分布式拓扑结构Fig.3 Distributed topology structure

3 算法设计

3.1 算法介绍

在本文场景中,由于电磁数据采集设备分布有多个并放置于不同地点,导致数据分散存储,并且采集的数据规模较大。如果使用网络传输,数据在通信过程中容易受到网络的波动,而导致数据不能实时共享。另外,中心化分布式方案采用的是主节点+从节点的模式运行系统。在这种情况下,如果主节点发生故障,很有可能导致系统崩溃。而去中心化的分布式方案刚好能够规避上述问题。由于去中心化分布式方案在训练过程中可以只在邻居节点间传递参数,大大减少了网络中的通信量,而且去中心化的分布式方案没有主节点,该方案中每个节点的地位都是等同的。理论上而言,任意节点宕机都不会造成系统的崩溃。采用去中心化的分布式训练方案,更适合本文的应用场景。

本文算法是去中心化分布式方案的一种,它由n个工作节点组成一个连通的点对点型网络,并协作解决一个一致优化问题。

(2)

式中:fi为工作节点i上待优化的目标模型,fi仅保留在工作节点i上,其他工作节点不可获取;x为模型参数。为解决上述优化问题,本文算法的所有工作节点仅和相邻节点进行信息交换,不需要一个融合中心(如参数服务器)来进行参数的同步,降低了拓扑网络的通信压力。

去中心化梯度下降不依赖于融合中心,它以下列方式执行梯度下降:

(1) 让每个工作节点i持有本地参数x(i);

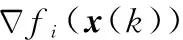
3.2 算法流程

算法1介绍了单个工作节点具体识别的算法流程,其中k为当前迭代序号,i代表当前节点序号,l表示总的迭代轮次。

算法 1 基于DSGD的电磁目标识别1 工作节点i(i∈{1,2,…,n})采集信号数据si2 对采集信号数据si进行预处理:滤波、能量检测、数据归一化、切片等,得到s'i3 对s'i进行STFT变换,生成数据集Di4 初始化模型参数x(i)(0),设置初始学习率α5 for k=1,2,…,l6 节点i根据本地数据集Di计算梯度 Δfi(x(i)(k))

7 发送梯度Δfi(x(i)(k))到邻居节点;8 接收邻居节点梯度,并进行加权平均: Δfix(i)k+12 =∑nj=1wijΔfj(x(j)(k))9 更新本地参数: x(i)(k+1)=x(i)(k)-αΔfix(i)k+12 10end for

本文采用点对点型的分布式拓扑结构,在算法1的流程中,当且仅当节点i与节点j相邻时,wij≠0,本文设置wij=1。

从上述算法中可以看出去中心化的梯度下降过程只依赖于相邻节点的参数数据,而不依赖于全局分布式节点的范围。在整个迭代过程中,每个节点仅需要发送本地模型梯度到邻居节点,且通信只存在于相邻节点之间,极大地减少了通信量。虽然整个模型迭代的时间变长,但是避免了传统中心化中需要向中心节点传递参数而造成的网络大量通信的问题和节点故障的容错性问题。

4 实验与结果分析

在本节中,本文在采集的手机电磁目标数据上进行实验验证,主要从收敛速度、训练时间、内存占用和识别准确率这几个方面对比集中式方法和DSGD方法。

4.1 数据说明

本次实验使用7部手机作为识别目标,分别为两部荣耀10手机,一部华为P9手机,两部苹果6S手机,一部魅族X8手机,一部小米6手机。在屏蔽箱内采集手机发出的电磁信号,时域 8 192点数据,共采集4个批次、每个目标每个批次6 000条样本,取前3个批次的数据作为训练集,即训练集7个目标共126 000条样本,将第4个批次的数据作为测试集,即测试集共7个目标共42 000条样本。

在算法流程中介绍到,在对电磁目标信号数据进行训练之前,需要做相应的预处理。本文采取的预处理方式包括滤波、能量检测、数据归一化、切片,以及对信号进行STFT特征提取。在对每条样本进行STFT变换后,会生成一个224×224的复数矩阵,本文将实部和虚部分开,最终生成维度为2×224×224的样本。

图4分别是7部手机一条样本的原始时域图和STFT后的时频图。

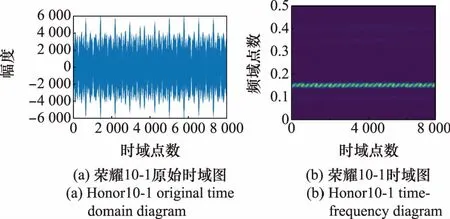
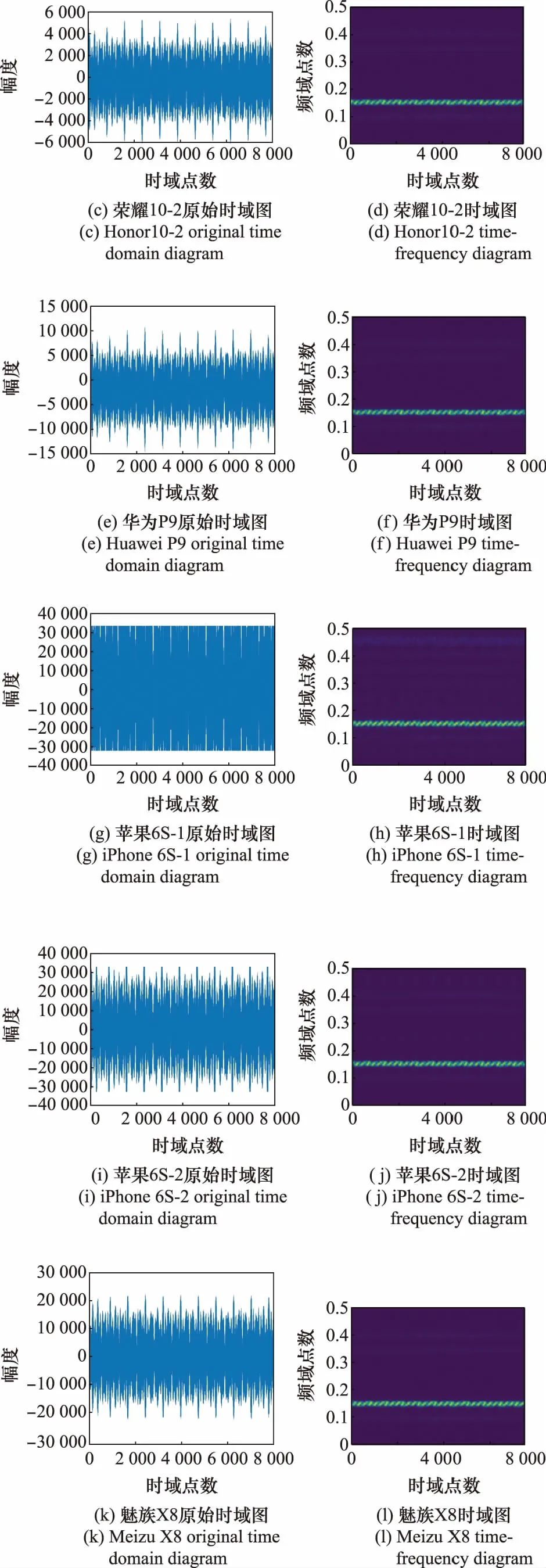
图4 时域波形图及STFT时频图Fig.4 Time domain diagram and STFT time-frequency diagram

4.2 实验设计

本文总共进行了8次实验,分别为集中式场景2次,分布式场景6次,均在搭有8块NVIDIA V100的GPU服务器上进行。

在集中式场景下,仅使用1块GPU。网络分别选用ResNet101和MLP-mixer以进行实验。

在分布式场景下,为了探究不同节点数的影响,本文进行了n=3、4、5这3种不同节点数的实验;为了探究对于不同神经网络的适用性,分别选取了ResNet101和MLP-mixer进行实验。在该场景下,每次实验选用n块GPU来分别代表n个节点,并将数据均分到n个节点上,搭建如图1(e)和图1(f)的点对点型通信拓扑结构。其中,每个节点向邻接节点广播本节点的模型参数梯度值,在节点接收到所有邻接节点的模型参数梯度值后,再进行本地模型参数的更新,具体更新方法见第2.1节算法介绍。

为了便于对比集中式场景和分布式场景的实验结果,保证实验的有效性,本文在每次实验中的硬件选择和网络参数设置保持一致。具体设置如表1所示。

表1 参数设置Table 1 Parameter setting

神经网络环境均为Pytorch1.9.0、Python3.8,每次实验共训练100轮。

4.3 结果及分析

经过8次实验,得到了不同场景中,分别在ResNet和MLP-mixer网络下训练的平均训练时间、内存占用、识别准确率等信息,如表2所示。

表2 训练结果Table 2 Training results

本文对分布式场景下的多节点识别准确率进行求和平均操作,并取前60轮的结果,得到了不同训练网络各场景下识别准确率随迭代轮次的变化,如图5所示。图6为分布式场景下5节点与集中式场景下使用ResNet网络训练得到的训练集识别准确率的变化曲线。由图6可知,在ResNet网络下训练,模型会很快收敛,并保持90%以上的识别准确率,且分布式场景下的训练效果与集中式相差不到1%。

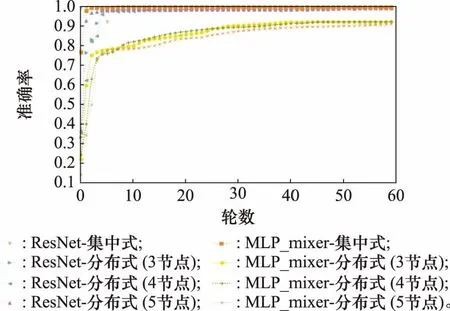
图5 训练集平均准确率变化曲线Fig.5 Average accuracy change curve of training set

图6 训练集准确率(ResNet)Fig.6 Accuracy of training set(ResNet)

图7为分布式场景下5节点与集中式场景下使用MLP-mixer网络训练得到的训练集识别准确率的变化曲线。相比ResNet网络下的训练过程,在采用MLP-mixer进行训练时,在分布式场景下收敛较慢,但最后也能达到92%以上的识别效果。

图7 训练集准确率(MLP-mixer)Fig.7 Accuracy of training set(MLP-mixer)

由表3训练结果可以看出,不同的网络结构,在训练集上的识别准确率相差6%左右,在测试集上的识别准确率相差1.5%左右。考虑神经网络容易拟合训练集上的数据,所以测试集上的准确率更有参考价值。可见本文方法可以适用于不同网络。

随着节点数的增加,单节点的样本数量有所减少,训练过程中占用的内存也会相应降低,也能有效减少平均训练时间,但是识别效果几乎没有下降。若单节点性能受限,可以在本文方法的基础上通过横向扩充节点数量来降低单节点上的识别压力,且不会对识别效果产生很大影响。

5 结 论

在现今复杂的战场环境下,海量数据的分布式数据分析显得十分重要。战场的电磁信号是基于作战任务相关的,不同用途的雷达、通信网,不同位置、不同时间所截获的电磁信号及活动特征之间存在着密切的协同关系。准确识别电磁信号类别,对提取电磁信号,了解敌方意图、作战行动等目的十分重要。本文提出了对海量电磁信号的去中心化的分布式解决方案,能够在性能有限的分布式节点间训练出有效模型,从而为电子对抗、联合火力打击决策支持提供情报分析结果。