基于CFD 模拟的技术供水系统沉沙池优化设计

赵栋栋，陈 嵩，陈 迅，钟永高

（四川华能太平驿水电有限责任公司，四川 成都 611830）

1 引言

水电站中的沉沙池具有沉淀作用，保证出池水流中泥沙颗粒含量在合理范围内，防止泥沙对后续设备造成损坏。不合理的沉沙池设计不仅会导致出口泥沙含量超过允许范围，还可能造成沉沙池中泥沙淤积速度过快，人工清理成本过高等不利状况。本文通过计算流体力学（Computational Fluid Dynamic, CFD）方法，结合离散相模型（Discrete Phase Model，DPM），利用商用 CFD 软件，检验某水电站沉沙池结构的合理性，并在结果的基础上提出合理的优化措施，为提高水电站沉沙池沉沙效率、保证安全运行提供保障。

数值研究方法广泛的应用于沉沙池的相关研究中，刘德伟 等[1]对优化后的沉沙池同时进行了试验和数值模拟的研究，结果表明，沉沙池优化后，沉沙效果以及冲沙效果基本上满足设计要求; 经过优化后，在沉沙工况下，沉沙池内水流流态平稳，符合沉沙要求的运行工况，便于泥沙沉降；在冲沙工况下，水流流速较大，确保了将泥沙冲出沉沙池。李顺涛 等[2]利用FLOW-3D 软件对沉沙池进行数值计算，对沉沙池的沉沙工况进行了模拟，发现沉沙池冲沙工况下，开始时流速快、冲沙速率较快，冲沙量大，随后逐渐减小，冲沙也趋于平缓。肖洋 等[3]对泥沙在水流中的运动状态进行试验研究，发现泥沙颗粒运动速度沿垂线分布，与水流速度不一致。赵志鹏 等[4]利用 DPM 模型研究沉沙池中泥沙流动状态，计算出了更加精细的结果。

这些对沉沙池的试验和数值模拟的研究证明了数值模拟对此类问题具有和试验同等的精度，DPM 方法能够较为精确地描述这种体积分数小于10%的颗粒流运动状态，但沉沙池的类型多种多样，需要具体问题具体研究[5-12]，因此，本文针对某水电站的沉沙池结构展开深入研究。

2 问题描述及控制方程

现太平驿水电站沉沙池长度约为26 m，宽度约为2.5 m，沿水流方向共 5 个沉沙区，其中，1 号和2号沉沙区各有4 个直径为0.2 m 的含沙水流入口，5个沉沙区底部中心各有一个直径0.1 m 的排污口。沉沙池使用现状表现为泥沙淤积程度高，池内淤沙需要经常清理，就此问题，展开现沉沙池的数值计算工作。

CFD 方法能最为经济且快速地取得现阶段泥沙流动状态，并且能够快速评价各种改造方法的效果，本研究选用了流态控制的连续性方程、动量方程，湍流的RNGk-ε 方程，如下所示。

连续性方程：

其中，u—速度；x，y，z—笛卡尔坐标系3 个方向。

动量方程组：

其中，ρ—密度；P—压力；v—黏度。

RNG k-ε 方程：

其中，Gκ—层流速度梯度而产生的湍流动能；Gb—由浮力而产生的湍流动能；Ym—由于在可压缩湍流中过渡的扩散产生的波动；C1，C2，C3—常量；ακ和αξ—k 方程和ε 方程的湍流Prandtl 数；Sk和Se—用户自定义源相。

3 模型建立

利用Solidworks2018 软件建立沉沙池三维物理模型，忽略池内爬梯结构，模型仅包括流体区域，未包含墙体和地基部分。

沉沙池的物理模型如图1 所示，包括8 个Φ200 mm 的进口，5 个Φ100 mm 的排污口及尾部的溢流口。

图1 沉沙池物理模型

4 计算网格划分

尺寸形状合理的网格能够加快收敛速度和提高计算精度，本模型结构规则性不强，因此选用四面体网格形式，四面体网格能够有效贴合不规则模型边界， 具有更高的灵活性。

选用ANSYS 软件中的 Meshing 软件对沉沙池划分网格，采用Proximity and Curvature 方法进行划分，在入口管道和底部溢流管处进行局部加密处理，经过网格独立性测试，最终选取的网格数目为89 651 个。考虑了边界层对流体的影响，边界层共5 层，增长率为1.2，边界层网格满足工程要求。对网格情况进行检查，未发现负网格情况，网格情况良好。最终总体网格质量优秀，扭曲度不超过0.8，完全满足工程精度。网格划分如图2 所示。

图2 沉沙池网格划分

5 模型介绍

本模型采用商用计算流体力学软件Fluent 进行计算分析，对于工程问题中固体颗粒体积占比小于 10%的条件，选用Fluent 软件中提供的离散项模型（Discrete Phase Model，DPM 模型）进行仿真，此模型的基本假设有：①颗粒在运动过程中，假设其无破损、变形等现象；②不考虑两相流中离散相颗粒之间的相互作用， 同时不考虑两相流中颗粒的温度变化；③假定离散相泥沙颗粒的物性参数指标为定值。该模型利用欧拉-拉格朗日方法计算颗粒的运动情况、尺寸分布和受力情况等。

颗粒所受的最重要的力为重力和曳力，本模型重力方向为y 方向，在操作环境中设置重力方向和大小，大小为-9.81 m/s2。流体和固体的相互作用为本模型最关心的内容，因此设置DPM 模型为双向耦合，该方式能够更好地描述流体和固体间的相互作用。在DPM 的物理模型中，激活了萨夫曼升力、虚质量力及压力梯度力，使模拟结果更加贴合实际。

颗粒入射面选择全部Φ200 mm 的入口面，为了研究入口粒径分布对沉降率的影响，进行了两种粒径模拟，一种是使用入射颗粒的粒径测量值的平均数0.16 mm，另一种是采用Rosin-Rammler 分布，将全部颗粒按照粒径分成若干组，每组颗粒直径由中间粒径的颗粒代表，颗粒的轨道由代表粒径计算得到。在研究颗粒粒径分布的方法中，Rosin-Rammler 分布函数使用最广泛，Rosin-Rammler 分布函数定义全部颗粒的粒径被分成若干个粒径组，对于划分的每组颗粒粒径组则是由一个颗粒(中间粒径的颗粒) 来代表，颗粒的轨道由代表粒径计算得到。Rosin-Rammler 分布函数通常表示为：

式中:Y为小于直径D的颗粒的质量分数；d为颗粒尺寸分布的中位径；n 为分布函数指数。

粒子类型选择惰性颗粒。颗粒的入口流量为0.016 kg/s，由肖洋 等[3]研究的结论可以知道颗粒的流速和水流速相差不是很大，本模型中选择粒子的流速随水流流速。

湍流模型采用k-e 双方程湍流模型，由赵志鹏等[4]研究推荐选择 k-e 模型下的Realizable 模型进行湍流特征的描述。

6 边界条件设置

实际沉沙池的水位基本达到上边界，而且本计算中重点关注稳定状态下颗粒的分布状态，因此流体选用稳态计算模型，颗粒选择瞬态颗粒。通用边界条件的详细设置情况如表1 所示，数据均来自于测量值的数据统计。其余边界条件在总计算结果表中予以展示。

表1 通用边界条件

沙子的密度为1 800 kg/m3，水的动力黏度为0.001 003 kg/m·s，密度为998.2 kg/m3。压力速度求解器选择SIMPLE 模式，均选择二阶迎风模式。初始化方式采用Hybrid Initialization 方法。

7 结果与分析

计算残差图如图3 所示，可以看出整个计算收敛性较好，各残差都呈现稳步下降的趋势。

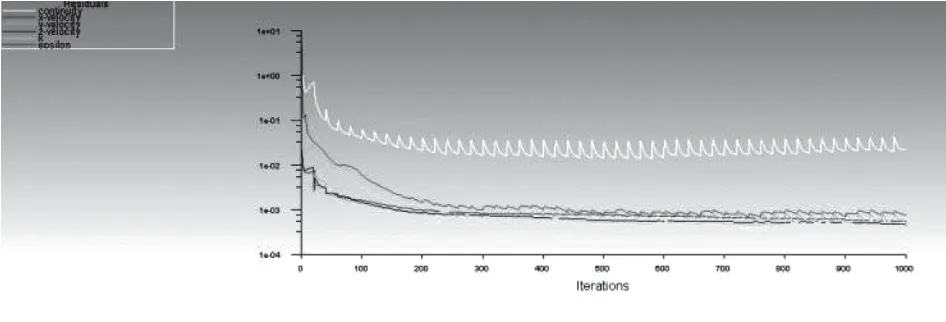
图3 计算残差图

图4 工况61、62、63 的3 种导流结构截图

图5 工况71、72、73、74 4 种改进方案截图

由于实际入口流速未取得直接测量结果，因此采用4 种不同的入口流速进行算例分析计算，每种入口速度分别进行均等粒径计算和Rosin－Rammler 分布粒径计算，泥沙密度采用的是DPM concentration 的流量数据，沉降率为滞留池内的颗粒除以入口颗粒，出口含沙量为出口颗粒除以入口颗粒。模型描述如表2 所示。

表2 模型描述

由表3 可以看出：

表3 模拟计算结果

（1）出口水含沙量随着入口水流速的升高而升高，而沉降率与入口流速的变化关系不明显，总体呈现下降趋势。

（2）随着入口流速升高底部排污口的泥沙含量降低，说明入口流速越大，底部排污口的排污效果越弱，更多的泥沙随着水流越过沉沙池，进入电厂设备，对电厂设备造成损坏的几率更高。

（3）采用R-R 分布粒径方法的计算结果比采用平均粒径方法的计算结果出口泥沙含量显著增大，主要是由于分布粒径的范围为0.03~3 mm，而平均值为0.123 mm，说明总体粒径偏小，粒径越小，越容易随水流前进，越不容易沉淀下来。

（4）扩大底部排污口直径可以有效降低出口水流中的泥沙含量，但随着入口流速增大，这种降低作用也会逐渐减弱，因此，控制入口水流速对降低泥沙含量十分重要。

（5）在沉沙池结构中加入数量较少的导流板均不能有效降低出口水流中泥沙含量，也不能降低沉沙量，这主要是由于导流结构的增加会加强水流的湍动，增加涡流，将水中泥沙翻滚起来，更加不容易沉降。

（6）现有沉沙池尺寸加宽2 倍和加长2 倍均能够降低出口水流中泥沙含量，如果再配以底部排污口直径增加，则能够显著降低出口水流中的泥沙含量，达到较好的沉降效果。

流线图如图6 所示，图中的线条代表水流的流线，颜色代表速度大小，可以看到入口处的速度较高，为设置的0.663 m/s，进入沉沙池后，速度大幅度降低， 这是由于流体的流动截面突然增大许多导致的。在1 号和2 号沉沙区内涡流强烈， 特别是在入口附近及底面排污口附近，出现强烈湍动现象。另外，从入口进入的流体在惯性的作用下有一部分撞击了入口对面的墙壁，结合图8 所示的颗粒轨迹图，1 号和2 号沉沙区的颗粒迹线最为集中，对比可以发现这种撞击能够有效提高大粒径泥沙的沉降，撞击后的泥沙运动方向发生改变，能量也有很大程度的损耗，更容易沉留在池内。另外，各沉沙区之间的溢流通道下方壁面也能够造成一定程度的流体撞击，加强沉降程度。

图6 流线图

图7 为流体速度渲染图和速度矢量图，在所有有弯折角度的地方流体的速度都较高，由渲染图可以明显看出，1 号和2 号沉沙区近壁面的位置速度较高，其余位置流速相对均匀，特别是3 号、4 号和5号沉沙区，速度非常均匀，在稳定流动的过程中，速度越均匀，沉沙效果越好，结合图7 的颗粒轨迹图也能看出，颗粒在最后3 个沉沙区中分布均匀。流体的湍动对沉沙效果带来负面影响，速度图中可以看出，1 号和2 号沉沙区内部湍动强烈，这种特征不利于泥沙的沉降， 同时，给底部排污口泥沙的排出也造成了负面效果。

图7 速度渲染图和速度矢量图

图8 是颗粒的轨迹图，颜色标尺表示颗粒的停留时长，颗粒在1 号和2 号沉沙区中湍动比较强烈，但由于撞击的作用，沉降程度也比较大，3 号、4 号和5 号沉沙区中的颗粒数目明显减少。

图8 颗粒轨迹图

综合来说，只要控制好入口流体流速，此沉沙池结构能够有效过滤水中粒径较大的泥沙颗粒，但是由于排污口尺寸过小，数目过少，沉积在池内的泥沙含量会随时间增加越来越多，需要定期的人为清理，但是排污口的尺寸如果过大，就会削减有效流体的流量，对后续设备产生影响，因此，可以考虑的改进方案有以下几种：①加长或加宽现有沉沙区尺寸，或控制沉沙池进出水流量不超过设计流量，降低流速，增加沉降率；②适当扩大底部排污口的尺寸，保证泥沙能够有效排出；③增加泥沙抽吸泵，从1 号和2 号沉沙区底部对淤积泥沙进行抽吸， 减少沉沙池中的淤积泥沙。

8 结论

本文利用计算流体力学方法针对某水电站的沉沙池结构展开深入研究，得出如下结论：

（1）沉降率随入口流速的升高而降低，出口水含沙量随入口流速的升高而升高， 入口流速越高，底部排污口排出的泥沙含量越低，应降低入口流速增加沉沙能力。

（2）均等粒径越小，出口含沙量越大，R-R 分布粒径方法比均等粒径法更贴合实际。

（3）底部出口直径越大，出口含沙量越低。

（4）增设导流板会导致出口含沙量大幅度升高，沉沙池应尽量做到沿出口方向平稳缓慢流动。

（5）去掉沉沙池底坡面会增加出口含沙量，加宽或加长原有沉沙池尺寸比基础工况均能提高沉降率，降低出口含沙量。说明沉沙池的尺寸和形状对沉降率和出口含沙量至关重要，在条件允许的情况下，应尽量扩大沉沙池尺寸，增大池底坡度。

（6）垂直于出口流动方向的撞击能够有效提高泥沙的沉降，撞击后的泥沙运动方向发生改变，能量也有很大程度的损耗，泥沙更容易沉留在池内。