针对带DFA防护SM4的SIFA攻击
谭子欣 胡永波 龚彦昊 胡春雅 张 琪 朱文锋 龚子超
(深圳市汇顶科技股份有限公司上海分公司脆弱性分析实验室 上海 201210)
自1997年Boneh等人[1]在RSA算法上成功实现了故障注入攻击并破解密钥之后,故障注入攻击在密码学领域以势如破竹之势迅猛发展.故障注入后的输出分为2种类型:一种是有效错误,攻击者可利用这种错误计算结果进行差分故障分析[2]、碰撞故障分析(collision fault analysis, CFA)[3]、统计故障攻击(statistical fault attack, SFA)[4]、故障敏感性分析(fault sensitivity analysis, FSA)[5]以及差分错误强度分析(differential fault intensity analysis, DFIA)[6]等一系列分析手段.另一种是故障未能影响输出结果,攻击者无法直接利用,通常称之为无效错误.
针对有效错误的故障注入防护方案通常有冗余防护[7]以及传染防护[8].冗余防护主要用于对称算法和非对称算法,传染防护主要用于对称算法.冗余防护即重复进行1次或多次密码计算,再将每次计算结果进行比对,仅当比对正确才将运算结果输出.传染防护即利用伪计算和冗余计算混淆至真实的轮运算中,当有故障注入到密码算法的计算中时,产生的错误将会逐轮次地传递下去,以保证密码算法无法输出对攻击者有效的错误输出,即有效错误.虽然传染防护可以避开单次输出检查防护所遇到的跳过检查的问题,但也需要通过检查输出保证密码算法正常的功能,以供用户使用.在以硬件实现密码算法的实际安全产品中,由于传染防护方案相对于输出检查防护方案增加了更多的逻辑布线,出于对算法实现开销的权衡,多采用冗余防护方案.
目前对于冗余防护方案的有效攻击方式有IFA和SIFA.IFA在2007年由Clavier[9]首次提出,该方案的创造性主要在于可以无需有效错误即可还原DES的密钥,同时还可以避开输出检查防护,但IFA需要故障注入精准到指令级别,使最后轮次的中间值产生固定错误,此类攻击方案对于故障注入的技术要求较高,依赖于特定的故障模型(如置0模型等),不易于实现.2018年,Dobraunig等人[10]提出了比IFA方案更加便于实现的SIFA方案,其不需要指定的故障模型,只要求输出结果与注入故障的中间值之间存在依赖关系,该方案分别对带冗余防护方案的AES算法和带传染防护的AES算法成功实现了SIFA攻击.SIFA方案除了无效错误相关的密文或明文,无需攻击者更多信息,因此在现实攻击中具有较强的实用性.
对于SM4算法[11],由于其本身是抗差分分析和线性分析的,所以目前比较有效的攻击手段主要是差分故障分析.如2006年Zhang等人[12]首次提出的对SM4的差分故障分析,仅通过约47条错误密文就能恢复128b种子密钥;2011年Li等人[13]提出了一种基于单字节错误模型的DFA方案,其恢复出128b种子密钥的平均计算复杂度只需要222.11;2019年,朱仁杰[14]针对SM4算法提出了一种扩大故障注入范围DFA方案,其破解出128b种子密钥的计算复杂度甚至可以降低至210;2020年金雨旋等人[15]提出了一种基于单比特故障模型的DFA方案,其恢复128b种子密钥的平均计算复杂度为215.3526.以上攻击方案都是针对没有防护的SM4算法,一旦带有冗余防护等DFA防护(即有效错误防护)之后,DFA分析便难以开展,所以为了对抗DFA防护,本文基于文献[10]的SIFA思想,对带DFA防护方案的SM4算法展开研究.本文的主要贡献为:首次针对SM4提出了一套抵抗DFA防护的随机明文SIFA方案,并以234的计算复杂度完成了对128b种子密钥的破解,同时给出了另外一套选择明文SIFA方案,该方案能够将攻破种子密钥的计算复杂度降低至212,从计算效率上优于大部分针对无防护SM4的DFA方案.
1 预备知识
1.1 带冗余防护的SM4方案
SM4是一种分组为128b长度、密钥为128b长度的分组密码,由于SM4是对称结构,其加密过程和解密流程共用一个结构.在安全产品的实际应用中,为了有效防止SM4遭受DFA攻击,最常见的做法是通过冗余保护阻止有效错误结果的输出,本文所使用的带冗余防护的SM4算法如下所示:
算法1.带冗余防护的SM4算法.
输入:P,K;
输出:C=SM4ENC(P,K).
① 计算C←SM4ENC(P,K);
② 计算P′←SM4DEC(C,K);
③ 如果P=P′,则输出C,否则生成随机数r并输出r.
1.2 带统计无效错误分析
SIFA的主要思想是通过故障注入,使得原本分布均匀的中间值变得不均匀,然后利用分布不均匀的中间值变量对真实轮密钥的偏向性,即受影响的中间值状态位对轮密钥位具有非线性依赖关系,同时其他错误密钥推导出的错误中间值会呈现出均匀的分布,再利用SEI或者CHI计算出非均匀分布与均匀分布之间的距离,从而区分出真实的密钥.
本文采用SEI来区分非均匀分布与均匀分布的偏差,当X={xi}i∈[0,n-1],X的SEI计算公式如下所示:
SEI(X)=
其中#{i|xi=δ,i∈[0,n-1]}表示集合X中xi=δ的个数.
2 针对带冗余防护SM4算法的SIFA
本节将详细介绍对带冗余防护SM4算法的SIFA实现,首先介绍基于随机明文的SIFA方案,然后再介绍为了降低攻击复杂度而设计的选择明文SIFA方案.
2.1 基于随机明文的SIFA
2.1.1 算法原理
在本文的攻击方案设计中,选择带冗余防护SM4算法(算法1)的步骤①(详见1.1节)作为攻击目标,对其第2轮中S非线性变换注入故障,图1展示了本文进行故障注入的具体位置.

图1 SM4前2轮算法框图

算法2.攻击算法A.
输入:明文集合Pgot={Pi}{i∈[0,3]},其中Pi表示Pgot中的第i字节组成的数据集;
输出:seimax,rsk.
① 初始化seimax=0,rsk=0,kguess=0;
② 计算temp=P2⊕P3⊕L(S(P1⊕P2⊕P3⊕kguess));
③ 计算seii=SEI(temp[j]),其中j∈[0,3],temp[j]表示temp中的第j字节组成的数据集;
④ 若{seii}i∈[0,3]中存在seik>seimax,则seimax=seik,rsk=kguess;
⑤ 计算kguess=kguess+1;
⑥ 当kguess∈[0,232-1],返回步骤②,否则进入步骤⑦;
⑦ 输出seimax和rsk.
在获得rsk0之后,采用同样的方式分别对第3~5轮的S变换进行故障注入,然后相继将rsk1,rsk2,rsk3解析出来,最后根据密钥扩展算法的流程,逆向推导出种子密钥K,故基于随机明文的SIFA方案的计算复杂度为234.
2.1.2 仿真实验
本文设计仿真实验如下:先设置密钥K=0x676F6F6469787661747261696E696E67,其首轮轮密钥为0x8A443F8C,然后随机生成1万条仿真明文数据M,再计算这些明文对应的中间值temp.为了构造出非均匀分布的temp集合,选择所有temp[0,:]∈(50,200)(即temp的第0字节的数值在50~200之间)对应的明文组成新的明文集M′,M′所对应的中间值为temp′,经过筛选后M′剩余5500条明文.图2展示了temp第0字节分布与temp′第0字节分布的对比图,其中图2(a)对应temp的第0字节分布,图2(b)对应temp′的第0字节分布.
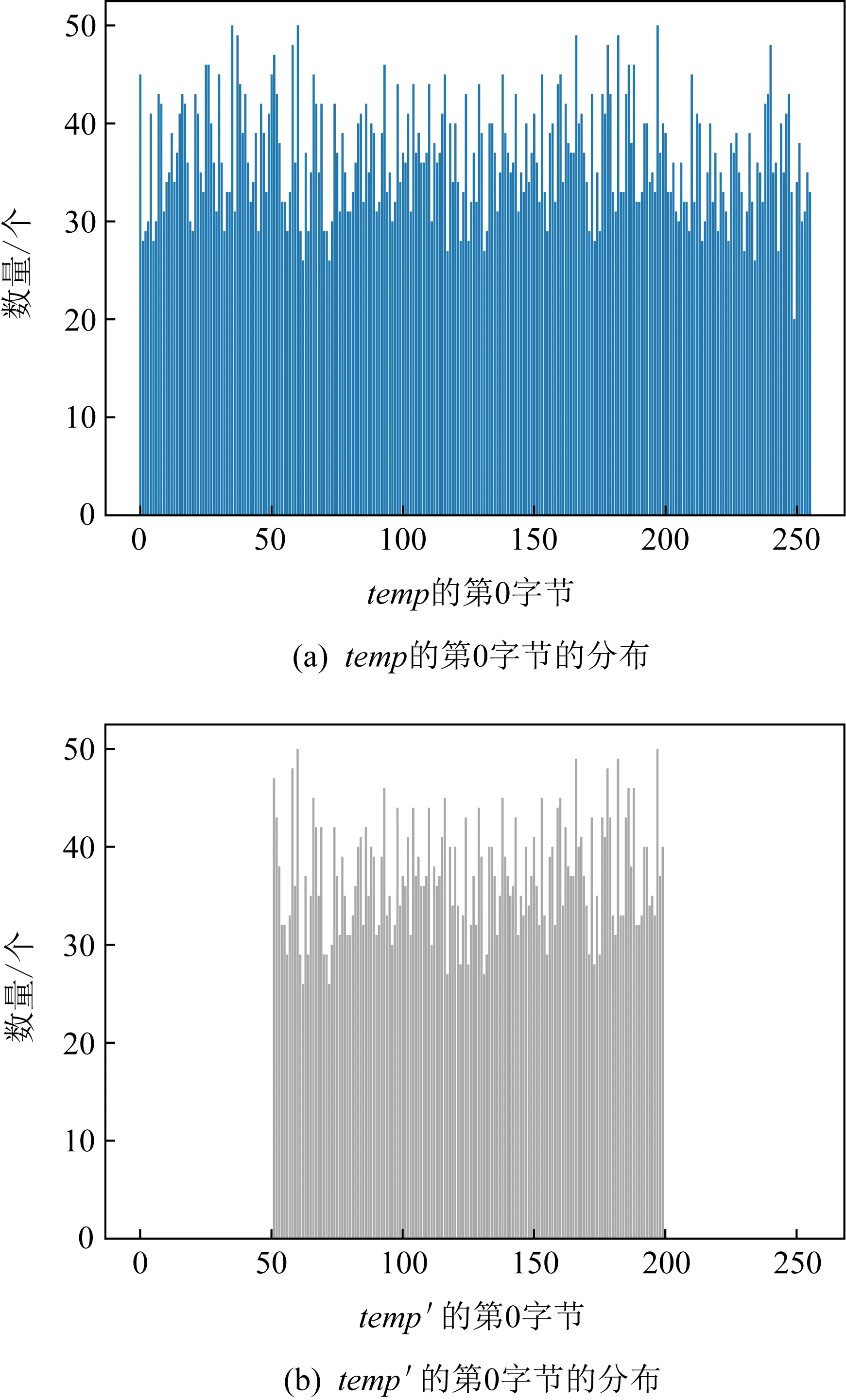
图2 第0字节分布对比图
然后将M′输入到算法2中,计算出所有候选密钥所对应的SEI值,由于候选密钥的范围较大,不宜在图中完整展示,故而本文选择了候选密钥范围为0x8A430000~0x8A46FFFF,横坐标共计196603个候选值,具体如图3所示,发现轮密钥0x8A443F8C所对应的SEI值高于其他错误轮密钥对应的SEI值,因此得出真实的轮密钥为0x8A443F8C.

图3 部分SEI-候选密钥对应图
2.1.3 基于STM32F103CT6的实际攻击
为了检验实际攻击的有效性,本文首先按照1.1节中的设计,将带冗余防护的SM4在keil软件通过C语言实现后,将其下载至单片机STM32F103CT6中,然后基于电压毛刺故障注入平台搭建环境,平台连接示意如图4所示:

图4 电压毛刺故障注入平台连接示意图
正常工作电压为3.3V,毛刺电压配置为0V,随机毛刺脉宽配置为500~550ns,电压毛刺的触发信号设在SM4第2轮轮计算开始位置.为了能让故障发生在S变换时间区域,配置毛刺延迟约为630ns,通过电压毛刺造成的瞬时掉电使得S变换功能紊乱,从而引入故障.
首先将SM4的密钥配置成固定形式,如K=0x676F6F6469787661747261696E696E67,然后传入2000条随机明文数据,在电压毛刺的故障注入下,有1799条数据由于触发冗余防护而输出随机数,剩余201条由于未触发冗余防护或者故障注入未成功而返回正常密文.将这201条明文输入到算法2,可以计算出所有候选密钥对应的SEI值,图5展示了候选密钥范围在0x8A430000~0x8A46FFFF的SEI值.其中0x8A443F8C所对应的SEI值最大,故而得到候选轮密钥0x8A443F8C为真实轮密钥.

图5 在实际攻击中部分SEI-候选密钥对应图
随后用真实轮密钥和这201条明文计算出中间值temp′,发现temp′呈现出单字节分布不均匀的特征,其中图6(a)中展示的第0字节分布表现出的不均匀特性尤为明显.

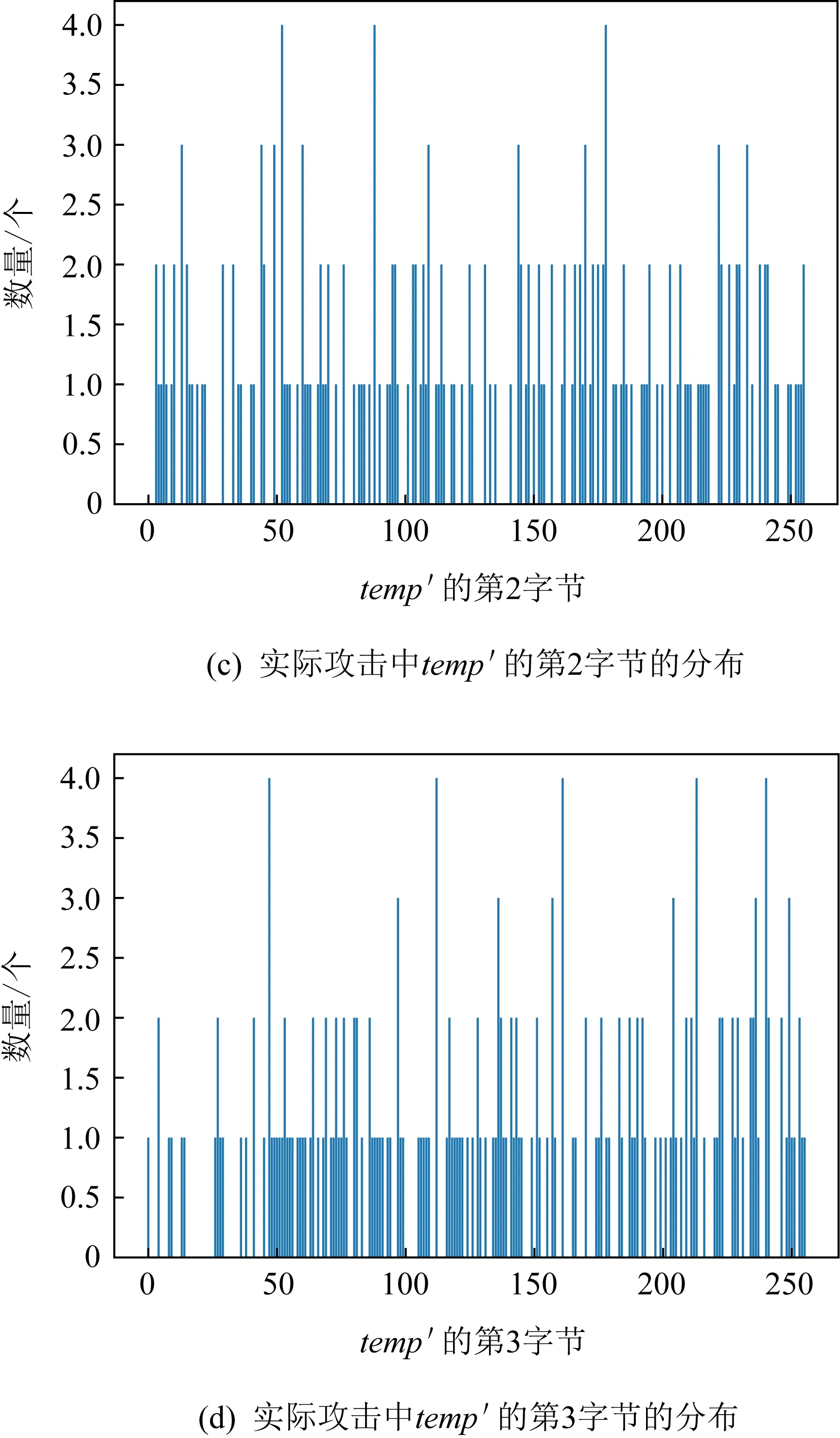
图6 实际攻击后temp′的字节分布图
2.2 基于选择明文的SIFA
2.1节所介绍的攻击需要对rsk0猜测232次,因此实现攻击的计算量非常大,本节提出一种选择明文攻击方式能够降低攻击的运算量,由于K0是一个固定值,而且X1⊕X2⊕X3⊕rsk0是一个32b的中间值,因此要计算出L(S(X1⊕X2⊕X3⊕rsk0)),需要猜测32b的密钥,当把X1⊕X2⊕X3⊕rsk0表示为4个独立的字节{t0,t1,t2,t3},有
L(S(X1⊕X2⊕X3⊕rsk0))=
L(S({t0,t1,t2,t3}))=L(S[t0]<<24)⊕
L(S[t1]<<16)⊕L(S[t2]<<8)⊕L(S[t3]).
假设能使t1~t3固定成任意常数,即固定明文X1⊕X2⊕X3的第1~3字节为常数,则L(S[t1]<<16)⊕L(S[t2]<<8)⊕L(S[t3])=α,α为常数,故而
L(S(X1⊕X2⊕X3⊕rsk0))=L(S(t0))⊕α,
然后可以得到
Y1⊕Y2⊕L(S(X1⊕X2⊕X3⊕rsk0))=
Y1⊕Y2⊕L(S(t0)<<24)⊕α.
此时要得到中间值temp=Y1⊕Y2⊕L(S(t0)<<24)⊕α,只需计算L(S(t0)<<24),而计算t0只需要遍历rsk0的高8b即可,即遍历rsk0[0].
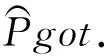
算法3.攻击算法B.

输出:seimax,rsk_bytenum.
① 初始化seimax=0,rsk_bytenum=0,t=0;
② 若bytenum=0,令e=S(t)<<24;
③ 若bytenum=1,令e=S(t)<<16;
④ 若bytenum=2,令e=S(t)<<8;
⑤ 若bytenum=3,令e=S(t);

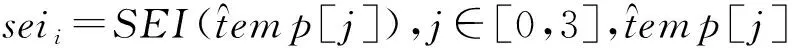
⑧ 若{seii}i∈[0,3]中存在seii>seimax,则seimax=seii,rsk_bytenum=t;
⑨ 计算t=t+1;
⑩ 若t∈[0,28-1],返回步骤②,否则进入下一步;
同理,用同样的方法分别攻击第3~5轮的S变换,直到破解出rsk1,rsk2,rsk3,最后再通过密钥扩展的逆运算获取种子私钥K.因此,本节方法可以将计算复杂度降低至212.
本文提出的SIFA攻击方案不仅可以抵御DFA防护,选择明文SIFA方案在效率上甚至优于现有大部分针对无防护SM4的攻击方案,具体如表1所示:
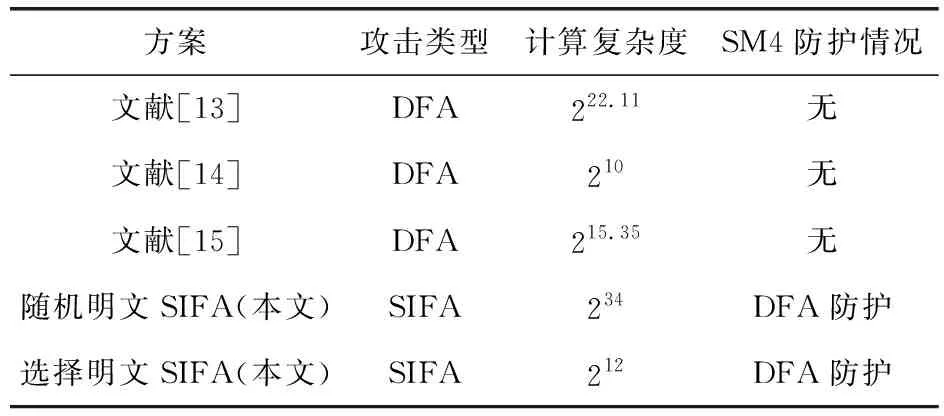
表1 本文方案与现有方案对比情况
3 结 语
本文首次提出了一套针对带DFA防护SM4的SIFA方案,并通过仿真进行了实验验证.同时,本文针对带冗余防护的SM4算法,在单片机STM32F103CT6上成功破解了密钥,计算复杂度为234.实验证明,只需要少量的带有无效错误的密文所对应的明文,便可实施攻击.另外还提出了一套基于选择明文的SIFA方案,能够将计算复杂度降低至212,从计算效率上优于目前大多数针对无防护SM4的DFA方案.
本文提出的针对SM4的SIFA攻击方案同样可以应用于带掩码防护的SM4方案以及带传染防护的SM4方案.对于带掩码防护的方案,攻击者需要对第2轮S变换进行注错,导致sout1的2条掩码数据发生无效错误,使得正确密文所对应的真实sout1依旧呈现出不均匀分布,攻击者通过重复加密过滤出正确的密文,再将正确密文带入本文提出的随机明文SIFA方案,破解出首轮的轮密钥,直至破解出SM4的完整密钥.而对于带传染防护的SM4方案,只需要通过重复加密过滤出带有无效错误的正确密文即可.
通过验证,也更加证实了SIFA策略对于带DFA防护的对称算法方案存在较大威胁,但从文献[10]的结果与本文的实践不难看出,SIFA策略对于攻击的时间位置依旧存在较大的依赖性,因为随着无效错误在正常密文中的比重减少,目标中间值的分布也将趋近于均匀分布,故给密码算法增加随机延迟防护或添加伪计算防护可以很好地提高SIFA攻击难度,从攻击复杂度上削弱SIFA的效率.

