Generation of hyperentangled photon pairs based on lithium niobate waveguide

Yang-He Chen(陈洋河), Zhen Jiang(姜震), and Guang-Qiang He(何广强),†

1SJTU Pinghu Institute of Intelligent Optoelectronics,Department of Electronic Engineering,Shanghai Jiao Tong University,Shanghai 200240,China

2State Key Laboratory of Advanced Optical Communication Systems and Networks,Department of Electronic Engineering,Shanghai Jiao Tong University,Shanghai 200240,China

Keywords: hyperentanglement,nonlinear photonic crystal,lithium niobate waveguide

1.Introduction

Quantum entanglement is a highly representative and attractive phenomenon in quantum physics, representing a fundamental quantum correlation in complex quantum systems.Quantum entanglement is widely used in various quantum applications and quantum technologies, laying the foundation for exponential performance acceleration of quantum computing,[1–3]safe and reliable quantum communication,[4–6]precise and sensitive quantum precision measurement,[7–11]etc.In quantum key distribution,the use of quantum entanglement enables the two communicating parties to share a random,secure key to encrypt and decrypt information,thus ensuring communication security.[12–14]Dense coding applies the quantum entanglement mechanism to transmit information, and for every two classical bits of information,only one quantum bit needs to be used,thus doubling the transmission efficiency.[15,16]Quantum entanglement also plays an important role in the architecture of quantum computers.For example, in a one-way quantum computer approach, a multibody entangled state, usually a graph state or cluster state,must first be prepared, and then the result is calculated by a series of measurements.[17,18]

Quantum entanglement can arise in multiple degrees of freedom, such as polarization degrees of freedom, spatial mode degrees of freedom,and time degrees of freedom.[19,20]Such quantum states with entanglement relations in multiple degrees of freedom are called hyperentangled states.Hyperentanglement has many advantages over quantum entanglement in single degree of freedom: it can realize more effective Bell state measurement, construct asymmetric optical quantum networks, improve the channel capacity of quantum networks, and can also contribute to the physical realization of quantum purification and quantum computing, and can be applied to the in-depth study of fundamental problems of quantum mechanics such as nonlocality.[21,22]Hyperentangled photon pairs have excellent information carrying capability and are very ideal physical carriers for quantum communication systems.Since the hyperentangled state has multiple degrees of freedom, it can improve the channel capacity and security of quantum communication, and plays an important role in many practical areas of application such as quantum information science.[23,24]

There are many schemes for the preparation of hyperentangled states.In 2015, Zhenda Xieet al.prepared highdimensional hyperentanglement with polarization entanglement and energy-time entanglement using a fibre Fabry–Pérot cavity(FFPC)and Hong–Ou–Mandel(HOM)interference.[25]In 2018, Chenetet al.achieved a polarization-based HOM interference-based preparation of polarization entanglement sources and extended it to the preparation of polarizationdiscrete frequency hyperentanglement sources in 2019.[26,27]However,these schemes can only prepare hyperentangled photon pairs of discrete variables and are difficult to achieve onchip integration.In our scheme,we will use carefully designed lithium niobate waveguides to directly generate hyperentanglement on a polarization and energy-time basis through spontaneous parametric downconversion(SPDC)process, and the generated two-photon pairs have a certain bandwidth.

This paper is organized as follows.In Section 2, we introduce our scheme that generates hyperentangled biphoton states.In Section 3, the SPDC Hamiltonian is introduced and we derive the theoretical model of hyperentangled twophoton states.Section 4 demonstrates that the generated twophoton pair exists entanglement in the energy-time dimension,which finally proves the existence of hyperentanglement for our scheme.Section 5 gives the conclusion of this paper.

2.The hyperentangled photon pairs source scheme

In our hyperentangled photon pairs source scheme, we chose a 600 nm thickz-cut lithium niobate crystal film as the base processing material and etched a specific structure of waveguide on the crystal,as shown in Fig.1.The trapezoid in the center of the figure is the area where the pump light,signal light and idler light are transmitted, and the length of the waveguide is 8 mm.The effective refractive index dispersion curves of this waveguide structure for o-light and e-light are obtained by simulation,as shown in Fig.2(θ=75°).

Fig.1.Scheme of our z-cut LN waveguide.(a) Overall schematic diagram.Purple arrows show the optical axis of LN and red arrows show the electric polarization direction of the transverse electric(TE)mode and the transverse magnetic(TM)mode.(b)Cross-section diagram.(c)Material refractive index of LN with different optical axes at 1570 nm.(d)Mode profile.

Fig.2.Effective refractive index dispersion curves for o-light and e-light(θ =75°).

We set the wavelength of the input pump lightλp=780 nm, and its angular frequencyωp= 2ω0= 2.4149×1015rad/s,whereω0denotes the center frequency of the signal light and idler light generated by SPDC.According to the equation of wave vectork(ω)=[n(ω)·ω]/c, we can obtainko(2ω0) = 1.7318×107m-1,ko(ω0) = 7.5741×106m-1,ke(ω0) = 8.0235×106m-1.A pump photon generates a signal photon and an idler photon, and the amount of wave vector mismatch of this nonlinear process needs to be provided by a periodically polarized crystal to compensate.In our scheme, we use single-period polarization to compensate only the wave vector mismatch amount when the signal light and idler light frequencies are equal, that is,kpp=ko(2ω0)-ko(ω0)-ke(ω0)=1.8205×106m-1.According to the theory of quasi-phase matching,the amount of wave vector mismatch that can be compensated by a periodically polarized crystal is related to the polarization period askpp=2π/Λ,then we can obtain the polarization periodΛ=3.4513 μm.

We expect a broadband SPDC to occur in which the wavevector mismatch is still within a small range when the signal and idler light frequencies are not equal.At this point,the periodically polarized crystal is no longer able to compensate exactly for the wave vector mismatch of the downconversion process.Let the difference between the signal light and the idler light frequency is Δω, and assume that the signal light frequency is distributed on the left side ofω0and the idler light frequency is distributed on the right side ofω0,then the wave vector mismatch at this time is

wherem,n=o,e denotes the polarization states of signal light and idler light.When the amount of wave vector mismatch is not fully compensated,the efficiency of the nonlinear process decreases according to sinc function, and the conversion efficiency is proportional to sinc2[(Δk·L)/2], whereLindicates the length of the waveguide.

We expect the generated two-photon pair has hyperentanglement on a polarization and energy-time basis.To achieve entanglement in the polarization dimension,we need to make sure that only one of the two phase matching conditions can occur.Figure 3 shows conversion efficiencies corresponding to all possible SPDC processes, including type-I and type-II phase matching conditions.Figure 3 also shows conversion results corresponding to different cutting angleθ.In our actual work, we chooseθ= 75°.From Fig.3 we can see that when the frequency spacing of the two-photon grows to 1.92×1011Hz (192 GHz) for the type-II SPDC process,the function value drops to 0, which indicates that the conversion efficiency drops to 0,and we define the frequency interval at this point as the bandwidth of the quantum entanglement source.On the other hand, the value of the conversion efficiency function for type-I SPDC process tends to zero(approximately the order of 10-8), so it can be assumed that type-I SPDC process does not occur.Type-II SPDC process includes two cases: o→o+e and o→e+o.Given that two cases have nearly identical conversion efficiency functions,we can conclude that the two cases have the same probability of occurrence, that is, the generated two-photon state,which demonstrates the generated two-photon pair is entangled in the polarization dimension.

Fig.3.Conversion efficiency curves of all possible SPDC processes.(a) and (b) SPDC processes satisfying type-II phase matching condition.(c)and(d)SPDC processes satisfying type-I phase matching condition.Conversion results corresponding to different cutting angles θ are also shown above.

After we make sure the generated two-photon pair is entangled in the polarization dimension, we just need to prove that they are also entangled in the energy-time dimension,then the hyperentangled state will be obtained.

3.Theoretical model of hyperentangled twophoton states

In this section, we will derive the theoretical expression of our hyperentangled two-photon states on the basis of the Hamiltonian.In the interaction picture, the evolution of the quantum state with time satisfies the following equation:[28]

where|ψ(t →-∞)〉=|0〉s|0〉i,and ˆHint(t)represents the nonlinear part of the three-wave mixing Hamiltonian that includes a pump photon annihilating and generating a signal photon and an idler photon,and its inverse process

where h.c.denotes the Hermitian conjugate, which corresponds to the inverse process of SPDC.Hence,the two-photon state|ψ〉(disregarding the dominant contribution of vacuum)is

We consider that the input pump light,due to its high intensity,can be treated as a classical electric field

whereAP(ωP) denotes the spectral amplitude of the pump light.The quantized electric field operators for signal light and idler light can be expressed as

wherem=s,i, andΛis the period of the structured waveguide.Substitute Eqs.(5)and(6)into Eq.(4),we can obtain

Moreover, we go from thek-space to theω-space, where we can write dk= dω(ng(ω)/c),then we can derive

B(ωs,ωi),C(ωs,ωi) andD(ωs,ωi) can be obtained by the same method.Given the fact that type-I SPDC process does not occur(which is mentioned in Section 2)in our scheme,we can assume thatC(ωs,ωi)≈D(ωs,ωi)≈0, thus we obtain the resulting biphoton state

4.Simulation results

In this section,we show the numerical simulation results of JSA and joint temporal amplitude(JTA)to explore the entanglement of the generated two-photon pair in the energytime dimension.The input pump light is a single frequency continuous laser with a wavelength of 780 nm and a full width at half maxima of 0.1 nm.The calculated and plotted frequency width is set toBW=192 GHz, and JSA of the generated two-photon pair is shown in Fig.4.

Fig.4.Modulus distribution diagram of JSA.

WhenA(ωs,ωi) can be split into the product of two univariate functions aboutωsandωi(i.e.,A(ωs,ωi) =A(ωs)A(ωi)), the generated state is separable; conversely, ifA(ωs,ωi) is not separable, the generated state is entangled,and this entangled state is referred to as a continuous frequency entangled state.[29]To investigate whetherA(ωs,ωi)is splittable,we can perform a Schmidt decomposition on it

whereλnis the Schmidt coefficient,ψn(ωs)andφn(ωi)are a set of standard orthogonal functions in the Hilbert space where the signal optical quantum state and the idler optical quantum state are located,respectively.λn,ψn(ωs)andφn(ωi)are solutions of the following eigenvalue equations:

withK1(ω,ω′)≡∫A(ω,ω2)A*(ω′,ω2)dω2andK2(ω,ω′)≡∫A(ω1,ω)A*(ω1,ω′)dω1.

Based on the eigenvalueλnobtained from the Schmidt decomposition,two quantitative indicators,entropy of entanglementSand effective Schmidt rankK,can be used to measure the degree of entanglement,which are defined as

Entropy of entanglementS ＞0 and effective Schmidt rankK ＞1 both indicate the presence of entanglement, and the larger value indicates the higher degree of entanglement.The joint-spectral amplitude is first normalized and then solved to obtain the Schmidt coefficients in the Schmidt decomposition.In the specific calculation,the discretization into 5001-dimensional vectors and matrices gives the 5001 eigenvalues, i.e., the Schmidt coefficients.The first 15 Schmidt coefficients, arranged from largest to smallest, are shown in Fig.5(a).More than one non-zero Schmidt coefficient in Fig.5(a)proves that the two-photon generated by this broadband entanglement source has the property of continuous frequency entanglement.The calculated effective Schmidt rankK=3.6532＞1 also proves the continuous frequency entanglement property.Entropy of entanglementSis calculated and the result is shown in Fig.5(b), whereSfinally converges to 2.1276; and the first four basis functions in the Schmidt decomposition are shown in Figs.6(a)and 6(b),from which we can see the orthogonality of each basis function.

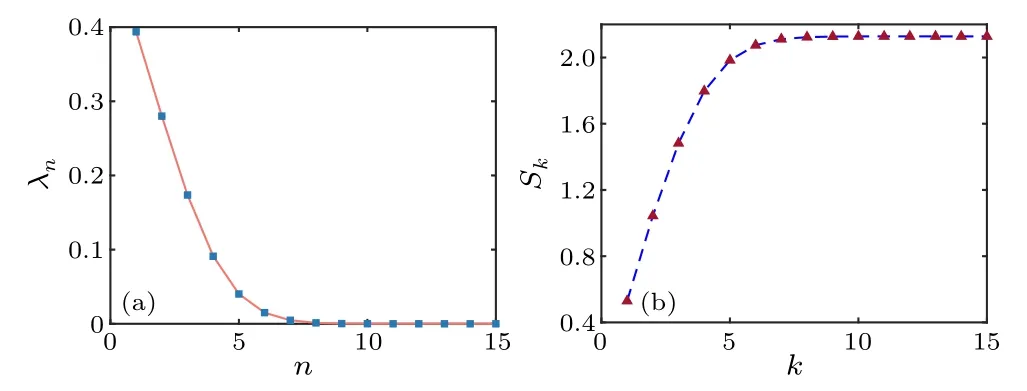
Fig.5.Results of Schmidt decomposition.(a)The maximum 15 Schmidt coefficients after Schmidt decomposition of JSA.The latter coefficients are close to 0, and their contributions to entropy of entanglement S and effective Schmidt rank K are negligible.(b) Entropy of entanglement S of our designed entanglement source.The results of successive iterations are shown,and Sk finally converges to 2.1276.

Fig.6.The first four basis functions (a) ψn and (b) φn after Schmidt decomposition.

After JSA is obtained, the Fourier transform can be used[30,31]to obtain JTA,with the relationship

The same entanglement analysis as JSA can be performed for JTA, i.e., continuous-time entanglement is judged by the Schmidt coefficients after Schmidt decomposition.After calculation,we obtain the exact same Schmidt coefficientsλnas JSA,which means that it also has the same entropy of entanglementS=2.1276 and effective Schmidt rankK=3.6532.Therefore, the two-photon state generated by this entangled source is also continuously time-entangled.

Next we will discuss the energy-time entanglement properties of the entangled source.Considering the signal photon and the idler photon generated by SPDC, the product of the standard deviation of the sum of their frequencies Δ(ωs+ωi)and the standard deviation of the difference in arrival times Δ(ts-ti) is called the joint uncertainty product.The joint uncertainty product less than 1 is the most direct manifestation and evidence of energy-time entanglement between signal light and idler light.[32]From our scheme we derive Δ(ωs+ωi)=9.0358×1010s-1and Δ(ts-ti)=4.5520×10-12s,therefore the joint uncertainty product Δ(ωs+ωi)Δ(ts-ti)=0.4113＜1,which demonstrates the energy-time entanglement property of signal light and idler light.Considering that in Section 2 it has been shown that the two-photon pair is also entangled in the polarization dimension,we successfully generate the hyperentangled two-photon pair in the polarization dimension and energy-time dimension.

5.Conclusion

This paper investigates a hyperentangled quantum entanglement source with a certain bandwidth based on lithium niobate straight waveguide.We verify the hyperentanglement in the polarization dimension by analyzing conversion efficiency functions of SPDC.The SPDC process is analyzed using quantum optics theory to obtain the theoretical model of the generated two-photon state.Corresponding simulation shows that the generated two-photon state also exhibits entanglement in energy-time dimension using Schmidt decomposition, which demonstrates that our entangled source generates a photon pair with a hyperentangled state finally.

Acknowledgments

Project supported by the Key-Area Research and Development Program of Guangdong Province of China (Grant No.2018B030325002), the National Natural Science Foundation of China (Grant No.62075129), the Open Project Program of SJTU-Pinghu Institute of Intelligent Optoelectronics (Grant No.2022SPIOE204), and the Science and Technology on Metrology and Calibration Laboratory (Grant No.JLJK2022001B002).