导数极值点偏移问题的解题表设计
——基于波利亚解题思想
孙雅琪
(华南师范大学数学科学学院,广东 广州 510631)
解题在中学数学教育中占据重要地位,对学生数学思维的完善起到很大作用.美籍匈牙利数学家乔治·波利亚(George Polya)认为中学数学教育的根本目的是“教会学生思考”,并通过《怎样解题》一书中所提出的“怎样解题表”给出了具体的实施方案.“怎样解题表”包括四个步骤:理解问题、拟定计划、实行计划、回顾,充分展现了学生应如何在一个“念头”的引导下进行层层递进地联想,这也为学生提供了一套解决数学问题的一般方法与模式[1].
1 解题表的设计
1.1 原题呈现
题目已知函数f(x)=x(1-lnx).
(1)讨论f(x)的单调性;
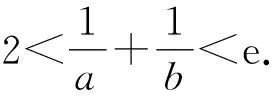
第(1)问根据导数和单调性的关系,可以快速得出f(x)在(0,1)上单调递增,在[1,+∞)上单调递减;第(2)问则是一个经典的极值点偏移问题,以此为例,基于波利亚解题思想,下文对极值点偏移问题的解题表设计进行探究.
1.2 理解问题
根据波利亚解题思想,当面对一道陌生题目时,学生首先要对题目所蕴含的信息进行提取,进而全面理解题目,结合“怎样解题表”,学生可从以下四个问题入手进行思考分析:已知是什么?未知是什么?条件是什么?满足条件是否可能?

进一步,结合f(x)图象,发现存在m,n>0,使得f(m)=f(n),且m,n分别在区间(0,1)和(1,e)内,又当x∈(0,1)时f(x)增长的速率比x∈(1,e)时f(x)下降的速率快,因此初步判断2 图1 f(x)的图象 结合以上分析,针对导数极值点偏移问题,可将问题具体表述为:该函数的解析式是什么?你能写出该函数的基本性质吗?能否画出函数的对应草图?你能判断两个未知数所在的区间吗?根据草图能否判断满足条件是否可能? 学生提取出本题所蕴含的信息后,接下来要建立已知与未知之间的关系,进而拟定出一个解决该题的计划,这一步骤很考验学生的逻辑思维,结合“怎样解题表”,可从以下三个问题入手进行思考分析:你以前曾经见过它吗?这里有一个与你有关且以前解过的问题,你能应用它吗?你能改述这个问题吗? 通过上文可知m,n分别在区间(0,1)和(1,e)内,不妨设m∈(0,1),n∈(1,e),显然本题无法通过作差、作商等方法直接对不等式进行证明,因此需借助其他方法:利用分析法,若2 g(x)=f(x)-f(2-x),x∈(0,1), h(x)=f(x)-f(e-x),x∈(0,1). 此时不等式证明问题就转化为求解函数的最值问题,通过求导判断g(x),h(x)的单调性,进而得到其最值,如果能得到g(x)<0,h(x)>0在(0,1)上恒成立,则可证得不等式成立. 结合以上分析,针对导数极值点偏移问题,可将问题具体表述为:能否直接判断m+n与2和e之间的大小关系?如果不能,你可以借助什么方法进行判断?如何判断两个可以变化的函数值的大小?你能构造出新函数吗?你可以在上述处理的基础上对题目进行改述吗?你能将新函数的值与0进行比较吗[2]? 这一步骤中,学生需依据前面所拟定的计划,对题目展开计算、证明,并对每一个步骤进行校核. 就极值点偏移问题而言,学生在实行上述计划时所面临的最大障碍往往存在于对新函数g(x),h(x)求导来判断其最值,进而证明其与0之间关系的过程中,但其中运算量却常参差不齐,本题恰巧可对其进行说明,具体如下: 令g(x)=f(x)-f(2-x),x∈(0,1), 所以g(x)在(0,1)上单调递增. 所以g(x) 即f(x)-f(2-x)<0,x∈(0,1). 将x=m代入可得f(n)=f(m) 因为n,2-m∈(1,e),f(x)在(1,e)上单调递减,所以n>2-m,即n+m>2. 令h(x)=f(x)-f(e-x),x∈(0,1), 则h′(x)=f′(x)+f′(e-x)=-lnx-ln(e-x), 所以h′(x)在(0,1)上单调递减. 因为当x→0+时,h′(x)→+∞,h′(1)=-ln(e-1)<0,所以存在唯一x0∈(0,1)使得h′(x0)=0. 当x∈(0,x0)时,h′(x)>0,h(x)在(0,x0)上单调递增,当x∈(x0,1)时,h′(x)<0,h(x)在(x0,1)上单调递减,因为当x→0+时,由洛必达法则知, 又f(x)在(1,e)上单调递减,所以f(1)>f(e-1).即h(x)=f(1)-f(e-1)>0.所以h(x)=f(x)-f(e-x)>0对于所有x∈(0,1)恒成立. 同理可得f(n)=f(m)>f(e-m). 进而有n+m 结合以上分析,针对导数极值点偏移问题,可将问题具体表述为:按照你所拟定的计划,你能否判断新函数的值与0之间的关系?若不能,你要如何进行改进?在计算过程中,你的演算是否正确? 在这一步骤中,学生首先应校核所得的答案,其次要梳理、反思本题的解答思路与过程,最后尝试在一种解法的基础上延伸出多种不同解法并进行推广,结合“怎样解题表”,可从以下三个问题入手进行思考分析:你能校核论证吗?你能用不同的方法得出结果吗?你能应用这结果或方法到别的问题上吗? 回顾本题的解答过程,当证明g(x)<0时,学生仅需对g(x)求一次导数且计算较易,而对于h(x)>0,学生不仅要求二次导数还需应用洛必达法则等超前知识,因此到这里大部分学生就会陷入迷茫,此时就需开辟新思路:前面所涉及的方法是在函数单调性的基础上通过构造新函数实现的,那么学生可以思考,能否对已知条件进行进一步处理,进而构造更易于计算的新函数?作为双变量不等式,可以想到将两个变量与某一个相同变量之间建立联系来减少变量个数,再关于该变量构建函数,而学生又至少有两种不同的方法来减少变量,既可以尝试通过换元处理得到新变量进而构造函数,也可以尝试利用放缩法减少某一变量进而构造函数.事实上,上述两种方法均可应用于此题,具体过程此处不再赘述. 结合上述分析,针对导数极值点偏移问题,可将问题具体表述为:你能核验论证吗?回顾这一解题过程,你能通过其它的方法论证这一结果吗?如换元、放缩.你如何将该题的解题方法应用至其他题目? (1)若f(x)≥0,求a的取值范围; (2)若f(x)有两个零点x1,x2,则x1x2<1. 应用上述解题表,可得表1所示的解题思路[3]. 表1 导数极值点问题的解题表设计在2022年高考数学全国甲卷第21题中的应用 本文基于波利亚解题思想,以2021年新高考数学全国Ⅰ卷第22题为例,对导数极值点偏移问题的解题表设计进行了探究,旨在为学生梳理解答此类问题的思路,提高学生的解题能力.而探究式的解题表设计则可以锻炼学生的逆向思维、发散思维以及创新思维,同时分析法的充分运用也可以锻炼学生自主思考的能力,这充分贴合波利亚所强调的“中学数学教育的根本目的是‘教会学生思考’”这一观点,也符合新课标中对中学生四基四能的要求.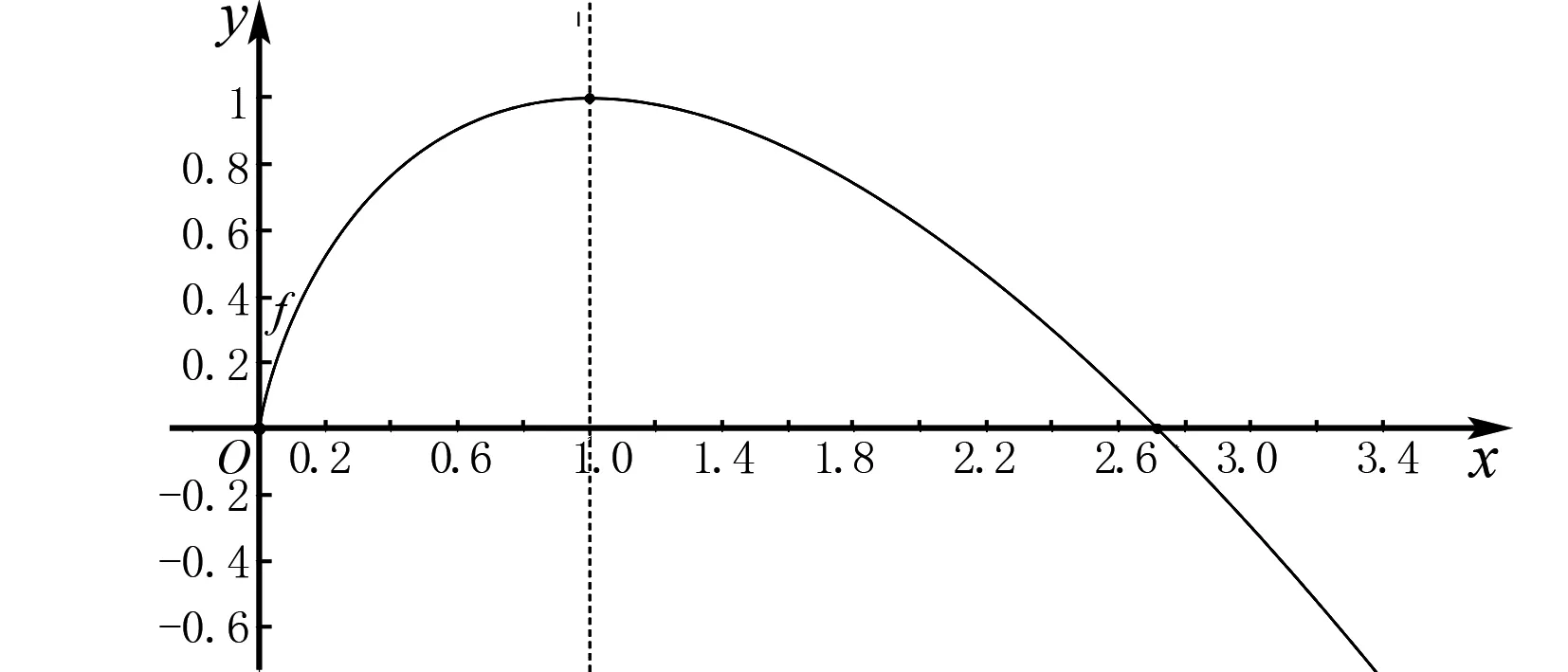
1.3 拟定计划
1.4 实行计划

1.5 回顾
2 解题表的应用
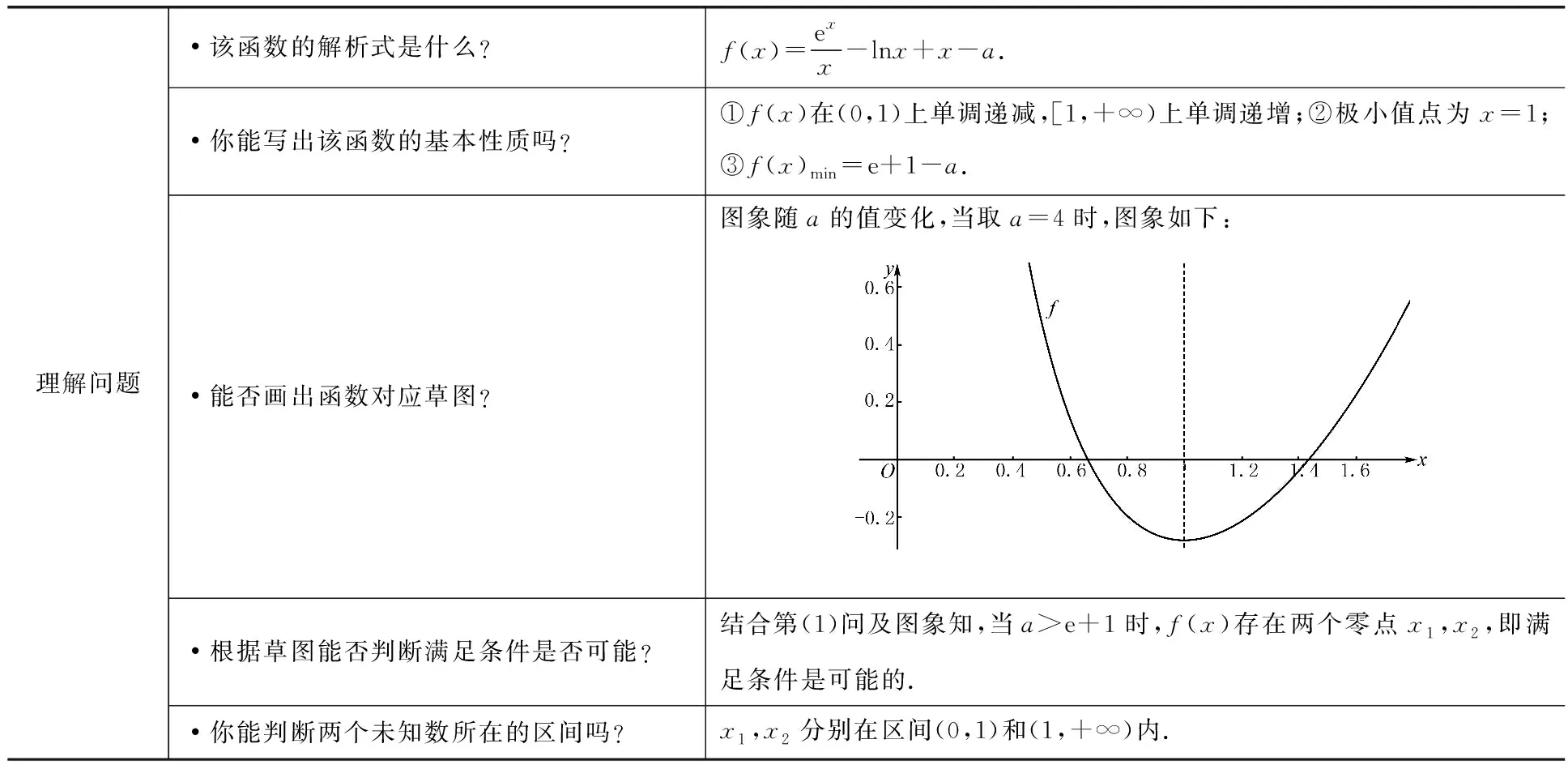
3 结语

